基于数字孪生的风机实时载荷预估研究

卢晓光，李凤格

(1.许昌许继风电科技有限公司，河南 许昌 461000；2.许昌智能继电器股份有限公司，河南 许昌 461000)

0 引言

风电行业在中国的迅猛发展，离不开新技术的持续变革与大力推动[1-4]。当前风电领域，平价上网已成为必然趋势，风电企业在风机安全运行得到保证之后，都在不遗余力地提升风机性能，增加风机可利用率[5-8]。当下急需风机技术变革来完成风机可利用率的进一步提升。作为风机运行效率的提升途径，实时掌握风机运行状态是一个突破口[9-11]。将风电机组的数字模型和风电机组的实际运行数据结合起来，实现风机载荷实时输出的技术可以为风机研发人员提供有效的信息，从而降低风机设计成本，增加风机控制手段，优化风机运行过程。

风电机组实时控制器中引入数字孪生技术的理念，通过风机数学模型与实时运行数据之间的交互，智能评估机组发电量与机组载荷之间的对应关系，生成有效的风机关键部件孪生载荷。实时载荷估计器在不需要额外增加传感器的情况下，可以估算风机的额外状态信息。本文基于以上数字孪生理念，研究了兆瓦级风电机组载荷估计算法的开发及验证过程。并以通用风电机组载荷仿真软件Bladed为工具，验证算法的预估效果。

本文首先建立风电机组在额定风速处的线性载荷实时估算模型；然后论证基于变增益思想的多个线性模型插值覆盖整个风电机组运行区间的方法；接着对估算载荷进行可靠性评估，并阐述评估载荷应用于疲劳载荷估算及实时控制的方法。

1 风电机组载荷预估模型辨识

风电机组数学模型具有复杂的模态及结构模式，然而机组模态能量大都集中在前几阶模态中，故此利用少部分机组模态，在正常运行期间即可捕获整个复杂模型中存在的绝大部分能量。风电机组数字孪生系统庞大，本文集中讨论其中的风机主要结构载荷部分，并针对塔架载荷及风轮推力载荷展开，目的是使研究结果尽快应用于风场柔塔控制及推力消减控制的改善上。

针对本文研究范围，估算器输入选择发电机转速、发电机扭矩和机舱加速度。此输入变量全部是目前风机已有的可靠测量设备所能检测到的量。因为这些变量受风机主要结构模态影响较大，对它们的观测可以反映机械模态的振动，能够由此构建一个线性的、可观测的系统来描述。

风机载荷线性预估模型搭建的重点为从选择的输入出发，寻找到风机载荷预估值输出的传递函数。传递函数首先被限定为线性函数，那么，只要辨识出线性函数的参数，则这样的传递函数即可被辨识。这个系统辨识的过程，或者说系统的参数化过程，即为训练。这个训练阶段需要输入和真实输出的时间序列，初步的系统辨识过程利用Bladed软件进行，依据软件输出的时间序列数据模拟创建。第2步可以使用实际风电机组的测量数据重复训练阶段。训练阶段的目标是最小化载荷线性预估模型输出与真实输出之间的平方误差之和。在此需指明，真实输出载荷在Bladed软件辨识阶段很好取出，软件可以直接输出。在实际风机辨识过程中，需要借助粘贴应变片采集。

本次辨识模型利用矩阵乘法来构建线性系统，进行输入到输出的映射。给每个输入输出对赋权重值，并对加权输入进行求和。其最优权重系数可以通过回归找到。研究过程中发现，仿射映射比线性映射能更好地完成输出值的辨识，因此对每1个向量式引入1个输入常量进行修正。此时，权重矩阵有1个额外的列，对偏移量进行建模。可用数学表达式表示此辨识模型，即

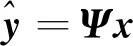
(1)

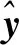
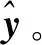
(2)

通过矩阵扩展、微分和重排，可得到最小二乘法目标函数的结果为

ΨΤ=(XTX)-1XTY

(3)

下面讨论以上动态辨识模型与估算载荷的适应性问题。如果输入输出之间的相位是相同的，则权重值取正值，反之，如果其相位差为180°，则权重值为负。不过，通常情况下输入和输出之间会有任意的相位和增益值。实际系统中，相位必定是滞后的，但是在训练中这个滞后量是无法得到的，因此通过在X中增加新的列，将多个备选滞后量添加到输入矩阵中，用于表示这种相位滞后。如果在上述优化过程中，可以在不明显增加预估值偏差的情况下移除这些备选滞后量，则直接移除这些备选量。

X的滞后列是通过现有的X阵列经相应的滤波器过滤创建的。这就保证了整个系统原有的线性特征，实现上只需添加少量的新权重参数进行优化，其在线运行非常简单，且起到信号噪声的抑制作用。滤波器从控制算法中的现有滤波器类型中选择，通过工程师经验调整滤波具体参数，但原则上能够通过数值的方式进行优化。附加滤波器可以提高载荷估计的精度，但精度不能任意提高，因为在载荷预估器中使用的是有限测量集，其不能覆盖到风机所有结构模态，只是对机组主要结构模态进行辨识建模。

2 风电机组载荷预估模型实时差值

变速变桨距风电机组的工作区间很大，一般机组会覆盖3～20 m/s的风速范围。风电机组控制算法设计人员通过配置1组非线性补偿器来解决模型通用问题。在额定发电机转速到额定风速之间，发电机转速通过转矩PI控制器进行调节。PI增益用于优化线性系统的性能，该系统是在转矩-速度控制器工作的条件下，对气动弹性模型进行线性化处理得到的。变桨控制过程中通过变增益控制算法实现额定风速以上风速段控制。这种增益变化的线性化控制器，组合成一个线性参数变化系统，即通常所述的LPV控制系统。

载荷估算器的全工况覆盖任务建立过程与此类似，在平均风速v1下从训练数据中得到的最佳权重矩阵，将同样应用在平均风速v2下进行载荷预估计算，其精度随着v1到v2的过渡逐渐降低。本方案对风速整个风速历程选取重要风速切片点，训练1组权重矩阵，每个风速选中点下，训练得到1个权重矩阵，当在线运行载荷预估器时，通过插值连接这些权重矩阵，实现整个运行风速区间的载荷预估器全覆盖。由于载荷预估器的状态由滤波器决定，滤波器是稳定的，所以载荷预估器的状态是稳定的。由于所估计的负荷是估计器状态的加权和，因此这些状态也是稳定的，与插值无关。

下面研究载荷预估器所用权重矩阵的调度实现。首先风速不能作为调度变量，在实际应用中风速风向仪测量信号是不可靠的。在额定风速以上，桨距角当前值是风速均值最可靠的反馈，而低于额定风速时，电机转矩是最可靠的风速均值反馈。这2个值可以用于调度变量，同时，这个调度变量在时间坐标上只有1个，而不是2个同时起作用。故此根据风机是否达到额定功率，引入加权系数，使用变桨角度或电机转矩的加权值进行权重矩阵的调度，在稳定状态下，上述变量对有效风速单调增加。根据平均风速下的训练数据，计算出最优权矩阵Ψi，并通过平均桨距角和平均转矩的加权和求出工作点γi。在风机运行时，对于任意时间步t，通过线性插值计算权重矩阵Ψ(t)，计算公式为

(4)

其中，γi<γ(t)≤γi+1。当γ(t)超出权重矩阵库选定范围时，意味着风电机组脱离其工作范围，此时为风机的非发电状态，权重矩阵要进行其他训练，本文暂不讨论。

3 风电机组载荷预估算例

现以许继某2.2 MW双馈机型为例进行风电机组载荷预估实验检测，风机自身参数因涉及敏感信息，在此不做公开。风电机组载荷预估器输入输出的变量坐标如图1所示。图1中，输入变量为桨距角β、塔架前后振动加速度aF、左右振动角速度as、发电机转矩Q、发电机转速Ω；预估载荷输出值为静止轮毂推力Fx，平面内力矩Mx，塔基前后弯矩Mx0和侧面弯矩My0。

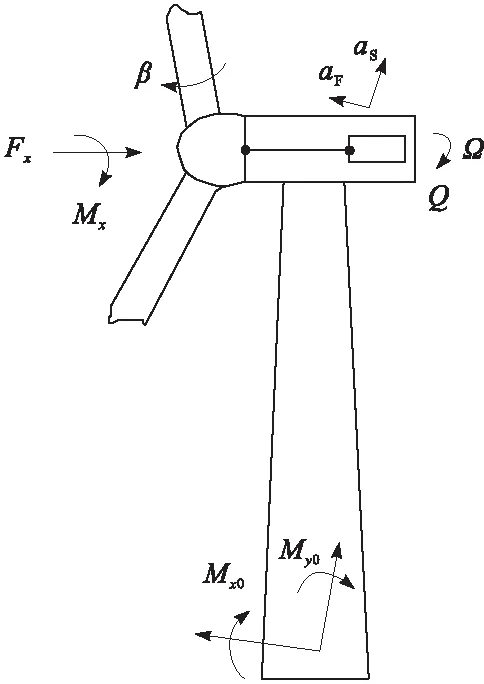
图1 风机变量坐标示意

本次实例训练使用的时间序列数据，由Bladed软件模拟的正常湍流模型下54个正常发电工况组成，即IEC标准规定的dlc2工况，每个工况为10 min数据。工况风速分布在4～20 m/s等间隔的平均风速下，每个平均风速由6个随机湍流种子组成。对于每个选定平均风速点，其中1组运行数据用于训练该点的线性载荷预估器权重矩阵，另外5个用于检测所得到载荷预估器参数的适用性。9个训练数据得到9个权重矩阵Ψ1～Ψ9，并得到如图2的工作点线性差值曲线。预估器运行时，根据此差值表进行权重矩阵系数调整。

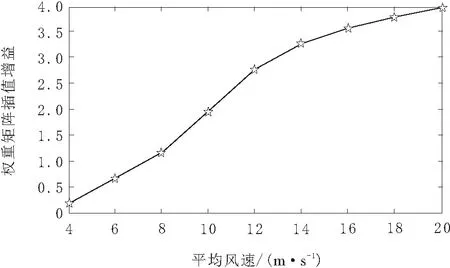
图2 线性加权系数差值曲线

图3～图6为额定风速附近的1组预估载荷与实际载荷的比较数据。其中,实际载荷为Bladed软件直接输出载荷。为清晰显示预估数据和实际载荷的差异，部分图片采用局部细节显示。需要说明的是，与实际风电机组一样，预估数据的计算只与上文输入量相关， Bladed软件实际输出载荷数据只提供比较依据。

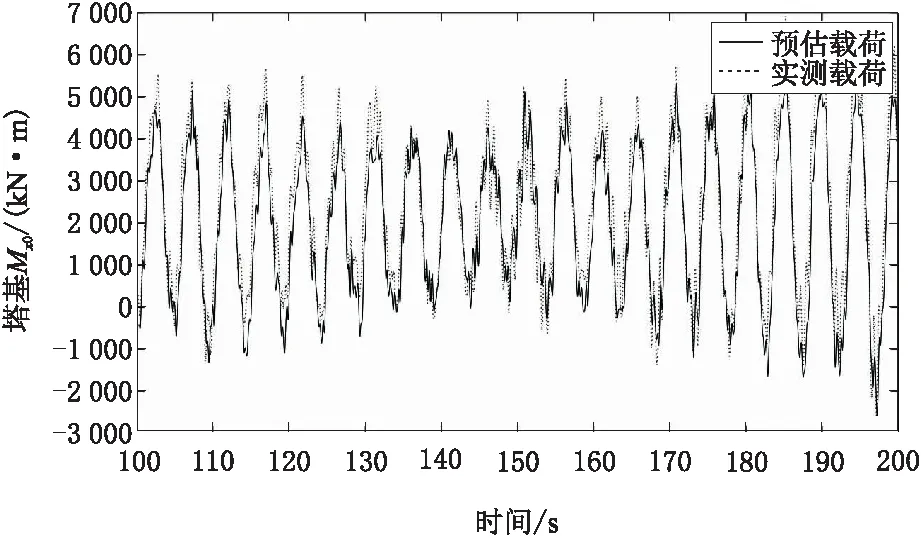
图3 塔基前后弯矩Mx0测量和估计值比较

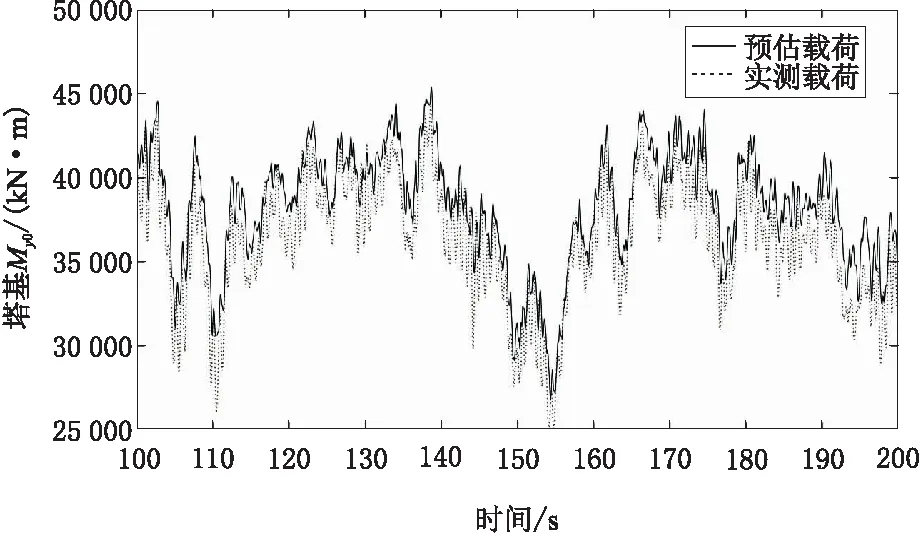
图4 塔基左右弯矩My0测量和估计值比较

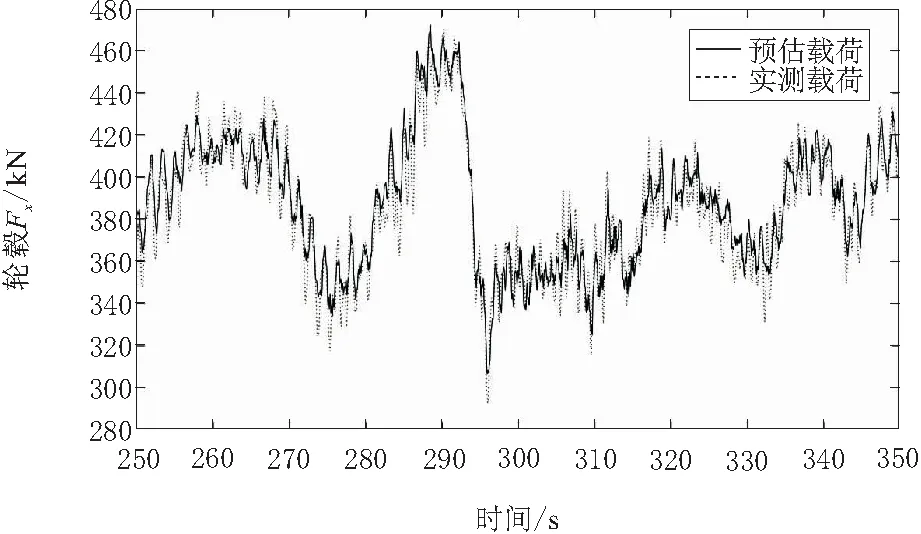
图5 轮毂推力Fx测量和估计值比较

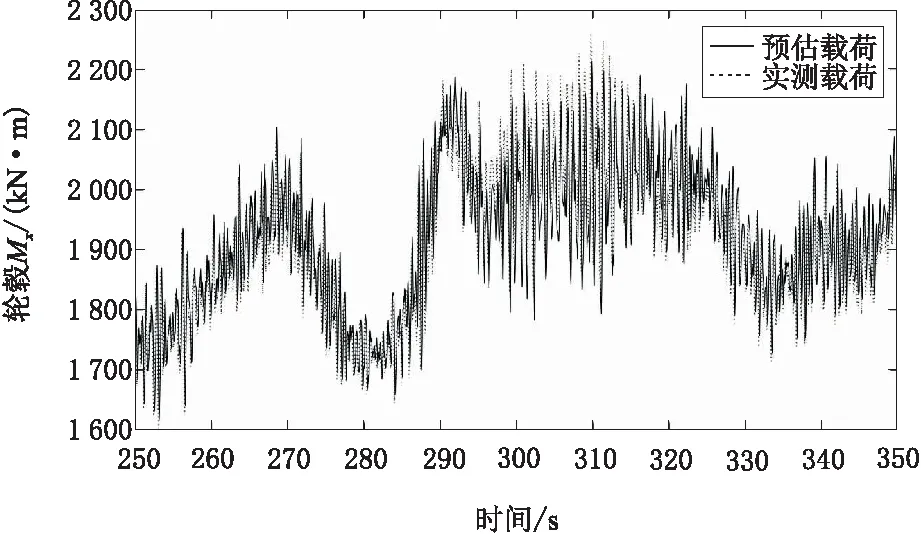
图6 轮毂扭矩Mx测量和估计值比较

由图3～图6的时间序列比较可知，载荷预估器估值精度是可以接受的，在频率较高的载荷波动中，控制器预估效果少差。估计负荷和实际负荷之间的微小差异，是由于载荷预估器没有建立风机模型高阶结构模态响应函数，这是已知误差。因此，估算载荷略微低估了疲劳载荷。然而，通过在大范围风况下测试载荷预估器，可以知道，每个荷载分量被低估的量是一致的和可预测的。因此，可以附加高频低估分量的修正系数来补偿这一已知误差。该系数为一般常数，通过补偿可使估计值与真实值之间的误差降至最低。图7为预估数据和实测数据的频域信息。由频域信息可以很清楚地看到估计值与真实值之间数据特征差异：在低频分量上，预估数据和实测数据重合度很好，这是预估模型所需要的。在高频分量上，预估数据几乎没有能量，而实测却有，但能量非常少，要利用对数坐标才能使高频分量能量显示清楚。

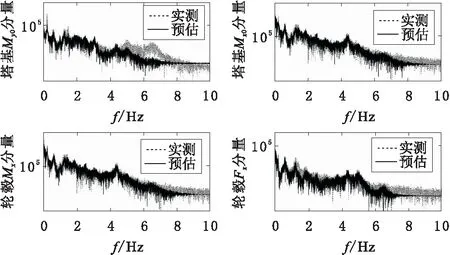
图7 频域测量和估计值比较

4 预估载荷精确度分析及应用

风电机组荷载估算的用途之一是进行风机的疲劳载荷估算。现利用风电机组载荷计算标准IEC所规定的风电机组等效疲劳载荷(damage equivalent loads,DEL)计算过程中的工况设置及计算方法，来设置工况并计算和评价预估载荷效果。

DEL是把实时载荷进行雨流计数，对每个bin的计数值，乘以适当的疲劳损伤比例因子得到，然后进行归一化处理完成DEL转换。整个仿真工况的预估载荷DEL记为De，实测载荷DEL记为Dt，Var为方差函数，然后定义精确度系数R2为

(5)

精确度系数代表估计疲劳载荷与真实疲劳载荷接近程度，其越大代表疲劳载荷预估越精确。

正常紊流条件下，从荷载估计器得到的54个模拟结果；在正常湍流条件下，从4～20 m/s的9个风速段下，可得到塔基的前后等效疲劳载荷标幺化后的结果。经计算，测定系数R2=99.32%。由此可知，预测的DEL误差小于1.00%。

9种不同风况下，4种预估荷载的精确度系数如表1所示。载荷预估器没有针对不同风况进行重新训练。精确度系数结果表明，预估器对风况不敏感。由数据可知，载荷预估经评估计算其精确度在96.00%以上，预测在不同工况下均误差小于4.00%。

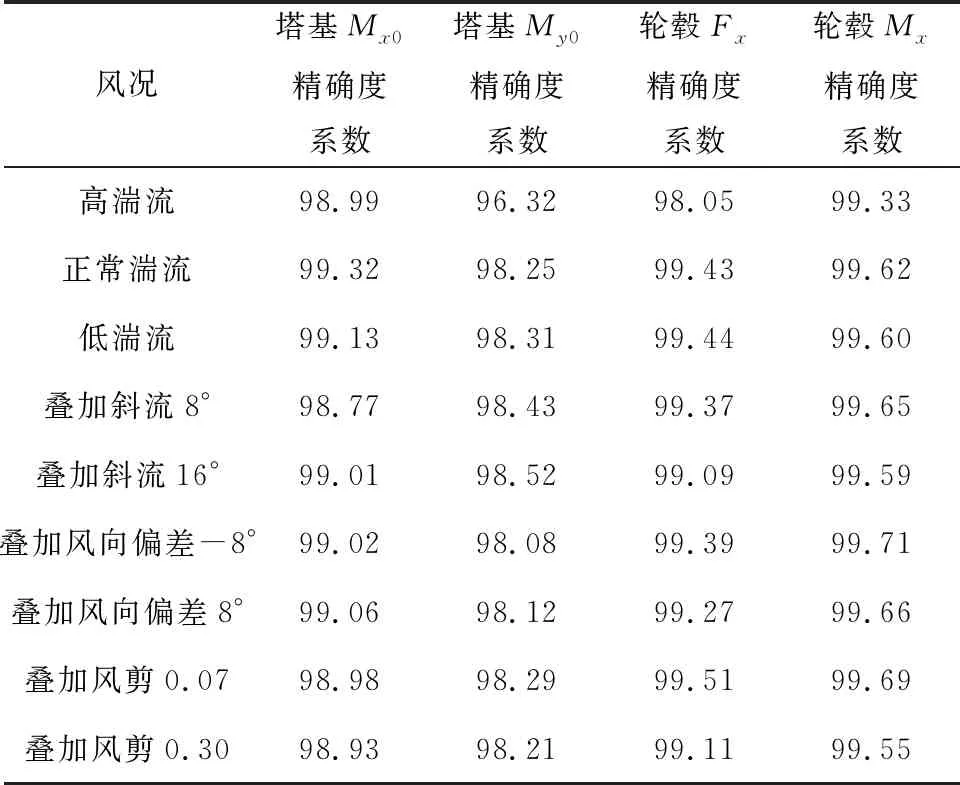
表1 9种风况下60次模拟的精确度系数 %

预估载荷的另外一个重要应用是帮助风机控制器进行实时降载。研究表明，风机在额定风速附近的风机推力最大，额定风速段风机推力会达到峰值，使叶片净空值小于安全值。此时，以预估轮毂推力为控制器输入，当达到一定阈值时利用适当收桨的控制手段，可以在发电功率损失较少的情况下减小轮毂推力，增加叶片净空值。图8为利用此算法进行推力消减的推力变化效果。数据显示，推力在额定风速附近消减明显，此策略导致叶片净空增加在7.00%以上。

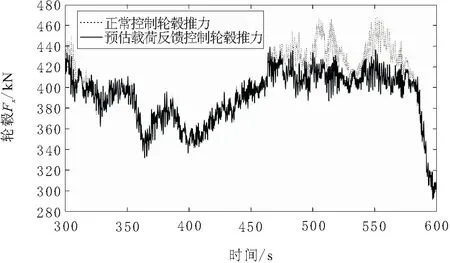
图8 预估载荷反馈推力消减比较

5 结束语

本文利用风机控制系统中已有的可靠测量值进行风机载荷预估，建立载荷预估模型；并通过权重矩阵的加权运算，实现估计器的输出。针对风机复杂非线性特性，文中给出了矩阵插值的具体实现方法，以使模型覆盖风机整个运行风速区间。

根据载荷预估方法，研究了载荷预估器在正常湍流风况下的额定风速附近的1个训练和输出实例。预估数据与实际载荷对比表明，模型预测载荷的结果精确度在各种风况下都能达到96.00%以上。

最后建立了预估载荷精确度的评价方法。预估精确度研究结果表明，在风电机组标准设计工况下，大多数载荷分量的DEL估计误差小于1.00%。此外，即使在高湍流大风切变等异常的风况下，预估载荷的DEL误差也不超过4.00%。

同时在预估载荷的控制应用上，简要给出了其在推力消减方面的应用实例，此部分更多的深入研究是后续研究的重心之一。