某船调距桨转叶力矩计算分析

张庆举，王德伦，张保中

（1. 大连理工大学 机械工程学院，辽宁大连 116024；2. 大连船舶重工集团 长兴岛船舶工程有限公司，辽宁大连 116005）

0 引言

调距桨（Controllable Pitch Propeller，CPP）转叶力矩是非常重要的参数，转叶力矩为桨毂强度校核、桨毂外形优化以及液压系统功率选择提供必要且可信的基本外部载荷。调距过程是一个非定常动态过程，桨叶离开设计螺距后，桨叶剖面发生畸变，水动力性能发生改变，使转叶力矩的计算变得更加复杂。调距桨转叶力矩涉及几何学和流体动力学等方面的知识，在试验条件和设备不齐全的情况下，按调距桨额定功率采用理论和图谱设计系数回归多项式进行最大转叶力矩估算不失为一种有效而经济的计算方法。某冷藏运输船调距桨按主机额定功率用图谱法进行终结设计后，需要进行转叶力矩计算。

1 调距桨参数及受力分析

1.1 调距桨参数

该船主机额定功率5 664 kW，额定转速520 r/min，经齿轮箱减速后调距桨工作转速为160 r/min。采用JDC4-55图谱进行调距桨终结设计，在主机额定功率驱动下的调距桨最佳要素为：船速V＝17.3 kn，螺距比P/D＝0.838 8，直径D＝4.51 m，盘面比Ae/A0＝0.55，η0＝0.584。

1.2 调距桨受力情况分析

调距桨吸收主机功率产生推力和转矩，桨叶旋转时产生离心力，流体对桨叶产生反作用的旋转阻力，旋转阻力因与桨叶盘面相切，因此也叫切向力。推力和切向力对桨叶根部产生弯矩，变距时桨叶受到转叶力矩作用。因此，桨叶受到推力、切向力和离心力作用，同时受到弯矩、转矩和转叶力矩作用[1]。

为研究计算方便，建立三维笛卡儿坐标系。以桨轴和转叶轴交点为坐标原点；以桨轴轴线为Y轴，航行方向为正；以转叶轴线为Z轴，离心方向为正向；X轴垂直于Y轴、Z轴所在平面，右舷方向为正。桨叶所受3力、3矩情况及笛卡儿坐标系见图1。其中，T为推力，FC为离心力，FQ为切向力，MT为弯矩，Q为转矩，QS为转叶力矩。

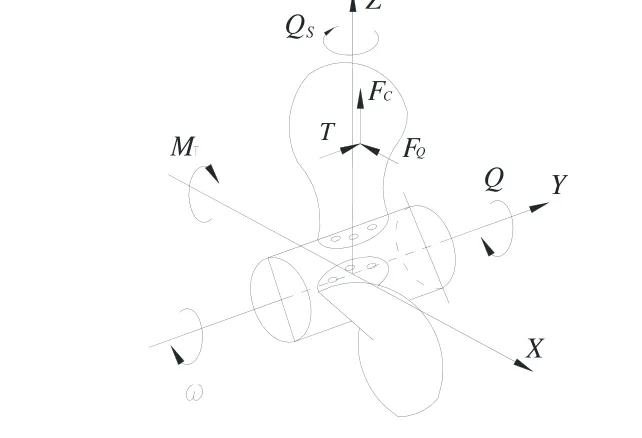
图1 桨叶受力及笛卡儿坐标系示意图

2 桨叶受力半径的计算

按图谱设计调距桨时，桨叶推力、切向力径向分布规律暂不清晰，假定推力沿径向呈线性分布，切向力沿径向均匀分布[2]。调距桨叶片重心半径可由桨叶切面积分得到，推力、切向力作用半径根据径向分布规律计算得到。桨叶受力作用半径见图2。

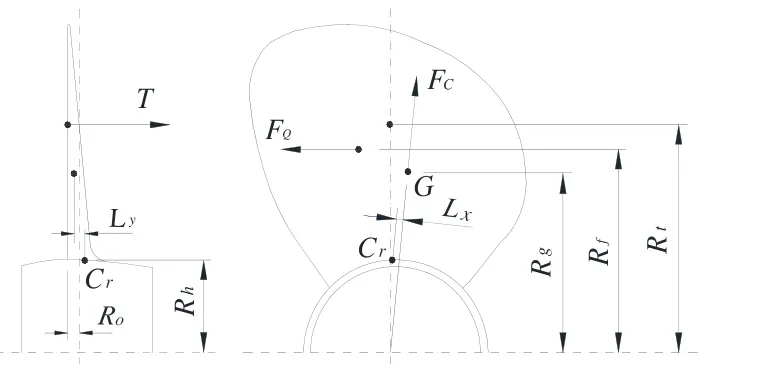
图2 调距桨叶受力半径示意图

图2中：Rg为重心半径，Rf为切向力作用半径，Rt为推力作用半径，Rh为桨毂半径，Cr为叶根切面形心，Ro为转叶轴至叶面距离，Lx、Ly为离心力力臂。

JDC4-55调距桨没有后倾，在主机额定功率驱动下工作时，桨叶侧斜0.272 m，侧斜角6.927°。桨叶轮廓几何尺度和叶切面坐标可通过查阅图谱计算获得[3]。

2.1 叶片重心半径的计算

沿径向把调距桨叶片分成12站，各站重心的zi坐标是各站高度中点所在的桨叶半径。调距桨叶片重量由各站重量组成，从0.277R至0.400R均分为6站，从0.400R至1.000R均分为6站，每站重量为

式中：ρ为桨叶材料密度，kg/m3；S为各站重心所在切面面积，m2；H为桨叶每站高度，m。

调距桨各站重心位置如表1所示。其中，xi表示从导边到重心的距离，yi表示重心到叶面距离占切面最大厚度的百分数。桨叶各站重心切面面积系数和重心位置计算系数见表1。

调距桨各半径叶切面面积为

式中：KS为各半径叶元体面积系数；b为各半径叶元体宽度，m；t为各半径叶元体最大厚度，m。则，调距桨叶片重心位置为

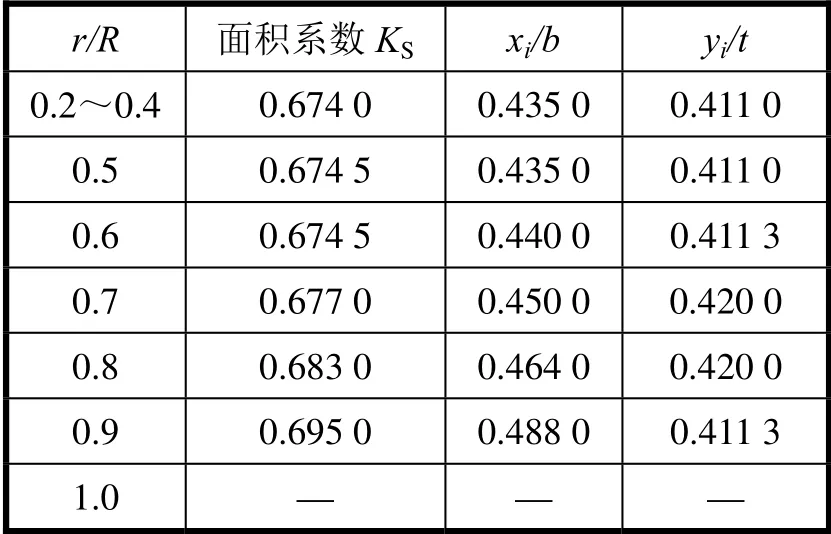
表1 桨叶切面重心计算系数表

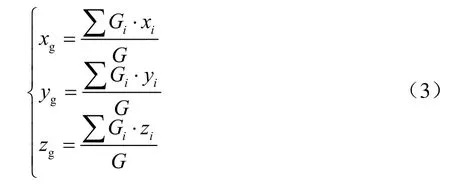
式中：xi为导边到叶片重心的距离，m；yg为叶面到叶片重心的厚度，m；zg为叶片重心到桨轴中心的距离，m；xi、yi、zi，为桨叶各站重心位置，m。桨叶各站重心坐标见表2。

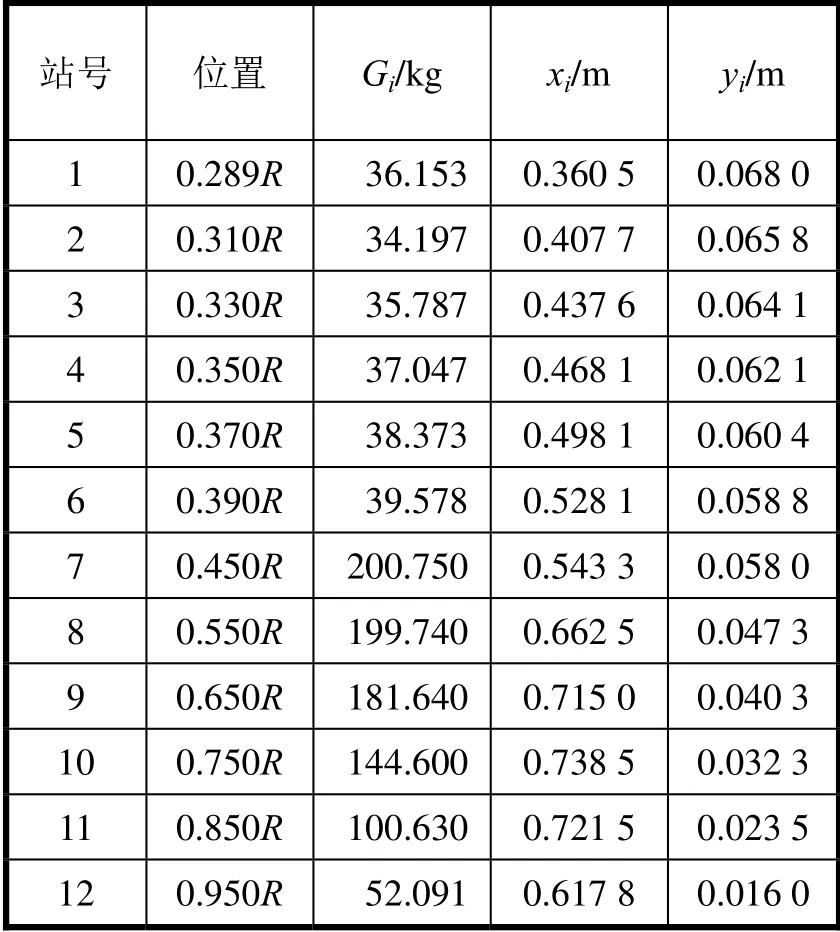
表2 桨叶各站重心坐标表

经计算，叶片重心位置为xg＝0.626 m，yg＝0.046 m，zg＝1.306 m，即叶片重心半径为Rg＝1.306 m。

2.2 推力半径的计算

推力沿径向线性分布为

桨叶推力力矩等于叶片各切面推力力矩之和，即

2.3 切向力半径的计算

切向力沿径向均匀分布为

桨叶切向力力矩等于桨叶各切面切向力力矩之和，即

3 调距桨转叶力矩的计算

调距桨的所有外来载荷都作用在桨毂壳体平面轴承上，桨毂平面轴承结构如图3和图4所示。

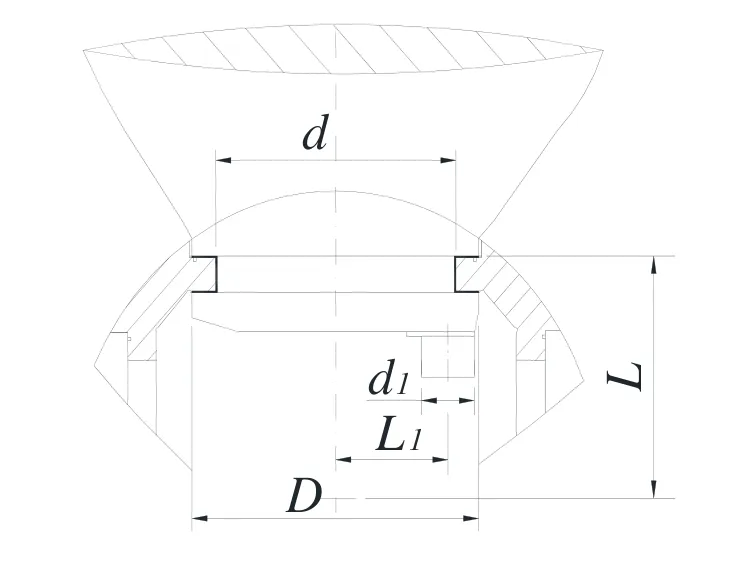
图3 桨叶-桨毂平面轴承结构示意图

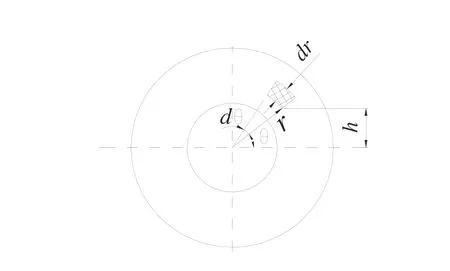
图4 平面轴承工作平面微元面积示意图

推力和切向力直接在平面轴承内圆柱面产生摩擦力矩，并通过弯矩在平面轴承上下平面产生摩擦力矩。调距桨旋转时，推力和切向力在桨叶上产生水动力转叶力矩，离心力在平面轴承下平面产生摩擦力矩；调距时，变距机构需克服摩擦力矩和水动力转叶力矩的作用。因此，调距桨转叶力矩主要由摩擦力矩、离心力转叶力矩和水动力转叶力矩组成。

3.1 合力在径向轴承产生的摩擦力矩

在主机额定功率驱动下，调距桨推力为464.98 kN，转矩为314.54 kN·m，切向力为FQ＝218.43 kN，则单个桨叶推力T1=116.245 kN，切向力FQ1=54.61 kN，推力、切向力的合力为F=128.433 kN。

合力在径向轴承产生的摩擦力矩为：

式中：u为钢与青铜摩擦系数，u＝0.15；d为平面轴承内圆直径，m，M1=5 376 N·m。

3.2 合成弯矩在平面轴承产生的摩擦力矩

推力、切向力通过桨叶在平面轴承上产生弯矩，弯矩对称于环形平面中性轴分别对平面轴承上下各半个工作面产生压力。

推力、切向力的合成弯矩为：

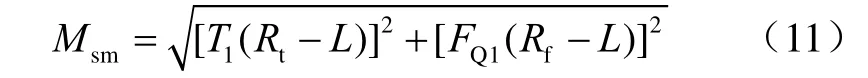
式中：L为平面轴承上平面至桨轴中心距离，L＝0.50 m；Msm＝1.371×105N·m。

平面轴承工作平面是环形面，该环形平面的惯性矩为：

式中：D为平面轴承工作平面外径，D＝0.676 m；d为平面轴承内圆直径，d＝0.56 m。

平面轴承环形工作面上任意半径r处的应力为

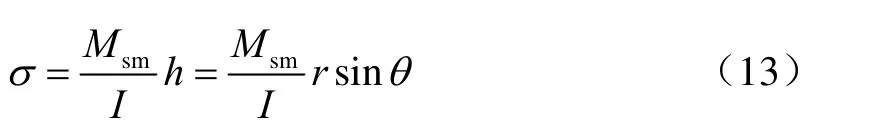
式中：Msm为推力、切向力的合成弯矩，N·m；h为平面轴承微元至中性轴的距离，m；r为平面轴承微元所在半径，m；θ为平面轴承微元与中性轴的夹角，(°)。

合成弯矩在平面轴承上下半平面产生的摩擦力矩为：

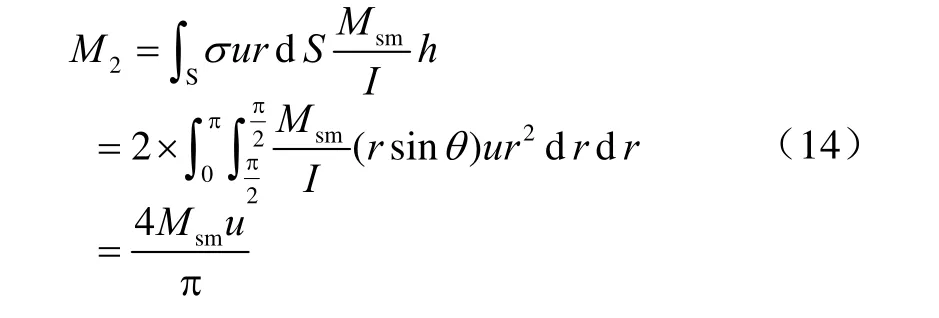
式中：M2＝26 197.45 N·m。

3.3 桨叶离心力在平面轴承产生的摩擦力矩

调距桨叶片与叶根法兰铸为一体，叶根法兰和曲柄销盘通过叶根螺栓刚性连接。调距桨旋转时，桨叶离心力由叶片、叶根法兰和曲柄销盘产生，离心力在平面轴承下平面产生压力且均匀分布。单个叶片重量为1 207.465 kg，重心半径为1.306 m；单个叶根法兰-曲柄销盘重量为579.915 kg，重心半径为0.46 m。则单个桨叶离心力为

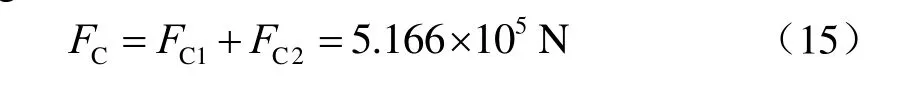
式中：FC1为调距桨叶片产生的离心力，N；FC2为叶根法兰-曲柄销盘产生的离心力，N。

平面轴承下平面单位面积离心力为：

则桨叶转动时，离心力产生的摩擦力矩为：

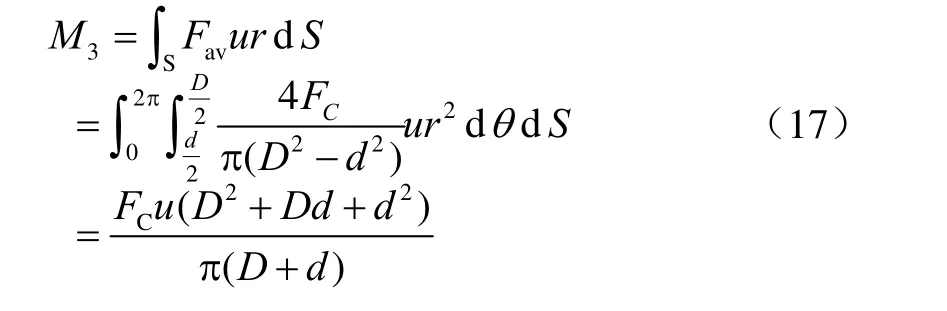
式中：r为离心力在平面轴承上的摩擦力臂，m；θ为平面轴承摩擦面微元夹角，(°)；M3＝22 944 N·m。

3.4 桨叶最大水动力转叶力矩计算

调距桨水动力转叶力矩主要受盘面比和螺距比影响，桨叶侧斜、纵斜和切面形状对其稍有影响，水动力转叶力矩的大小、方向随调距桨进速和螺距的变化而变化。在恒转速条件下，最大水动力转叶力矩通常出现在正倒车转换的零螺距附近。因此，按零螺距、零进速水动力状态计算调距桨最大水动力转叶力矩[4-5]。

3.4.1 设计桨螺距的修正

船舶行业标准CB/Z 813—2019中，标准4-55调距桨毂径比为0.265，0.7R处桨叶最大厚度比为0.015 4。主机额定功率驱动的调距桨螺距比为0.838 8，毂径比为0.277，0.7R处桨叶最大厚度比为0.017 1。因叶厚、毂径比不同，需对设计桨螺距进行修正，以便按标准桨参数进行水动力转叶力矩计算。

1）叶厚不同对螺距的修正

（1）叶厚变动量为

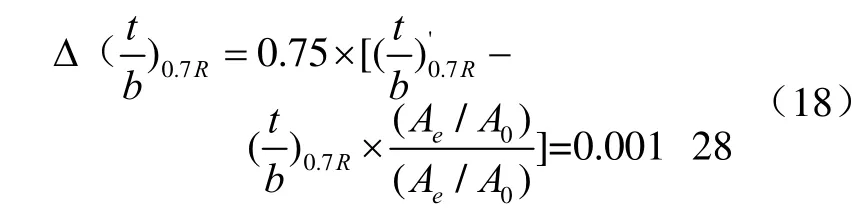
式中：(t/b)0.7R'为设计桨厚度比，m；(Ae/A0)'为设计桨盘面比；(t/b)0.7R为标准桨厚度比，m；Ae/A0为标准桨盘面比。

（2）叶厚对螺距修正的计算系数：

式中：Va为调距桨进速，m/s；N为调距桨转速，r/s；P为调距桨螺距，m。

（3）叶厚螺距修正量为

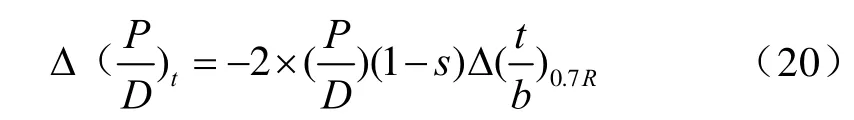
式中：(P/D)为设计桨厚度比。

2）毂径比不同对螺距的修正

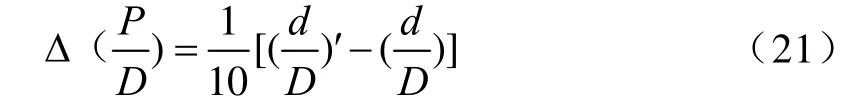
式中：(d/D)'为设计桨毂径比；d/D为标准桨毂径比。

3）修正后螺距

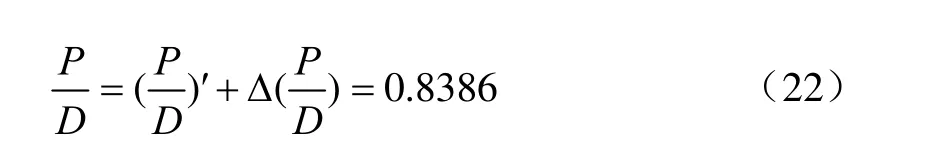
修正后与调距桨水动力性能完全相同的标准桨螺距比为0.838 6，毂径比为0.265 0。

3.4.2 调距桨最大水动力转叶力矩计算

调距桨在零螺距、零进速时水动力转叶力矩最大，可根据标准桨水动力转叶力矩系数回归多项式进行计算[6]。最大水动力转叶力矩系数为：

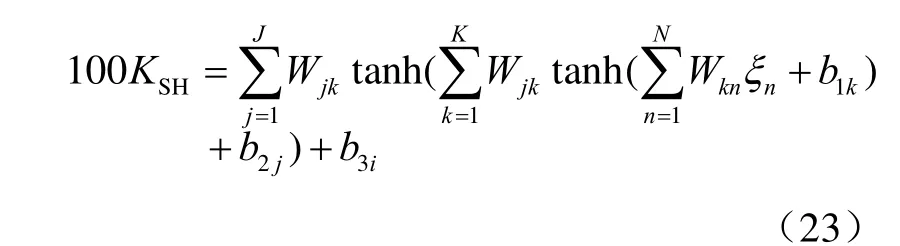
式中：KSH水动力转叶力矩系数；ξn为输入变量，依次为螺距比P/D、转角θ/50、进速系数J；N为输入变量维数；Wkn、Wjk、b1k、b2j、b3i为回归系数；K、J为系数矩阵维数；100KSH＝0.216 04。

调距桨水动力转叶力矩为：

由此可知：MSH＝29 381.79 N·m，单只桨叶最大水动力转叶力矩为7 345.45 N·m。

3.5 调距桨的最大转叶力矩

单个桨叶最大转叶力矩由额定功率时的摩擦转叶力矩、离心力转叶力矩和最大水动力转叶力矩组成，即：

式中：M＝61 862.9 N·m。

4 转叶力矩的验证

曲柄销盘销轴距转叶轴距离L1=0.26 m，转叶力矩对伺服油缸的作用力为

伺服油缸直径Φ800，油缸压力为

该冷藏船试验时，调距桨转速160 r/min，从全倒车到零螺距调距时的最大实测油压为1.81 MPa，误差4.74%，在工程允差10%范围内。

5 转叶力矩计算应注意的问题

1）摩擦力转叶力矩和离心力转叶力矩是按主机额定功率下调距桨额定工况进行计算的，如果偏离额定工况，推力和切向力可能发生变化，各转叶力矩需重新计算。

2）水动力最大转叶力矩是以零螺距和零进速水动力状态进行计算的，大部分调距桨都符合此规律。若桨叶为特殊设计或在某个特殊工况下，调距过程最大水动力转叶力矩发生在其他水动力状态，则最大水动力转叶力矩需重新计算。

3）计算过程中，摩擦力转叶力矩和离心力转叶力矩都是单个桨叶上的转叶力矩，水动力转叶力矩则是整个调距桨4个桨叶的转叶力矩。计算滑架推力校核油缸压力时，需计算4个桨叶对滑架的作用力。

6 结论

调距桨终结设计后，通过分析调距桨的摩擦力转叶力矩、离心力转叶力矩和最大水动力转叶力矩，计算调距桨额定工况下的最大转叶力矩和变距时的伺服油缸压力。通过实船调距试验，调距油压误差在允许范围内，验证了最大转叶力矩计算结果的可信性和计算方法的可用性。