基于改进Ortega观测器的内置式永磁同步电机无位置控制

王奇翔，罗 响，朱 莉，姜淑忠

(上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240)

0 引 言

内置式永磁同步电机(以下简称IPMSM)由于具有效率高、结构简单、动态响应快等优点，在电气传动中得到广泛应用[1]。在电机控制中，精确的位置信息对于实现高效控制至关重要。通常来说，位置信息是由高精度的位置传感器获得，如编码器、旋转变压器等。然而，这些位置传感器往往会导致成本、体积和系统复杂度的增加，同时也一定程度地降低了系统的可靠性[2]。

因此，近年来，电机的无位置传感器控制技术发展迅速，其主要可以分为两类：基于反电动势观测器的无位置控制和基于高频信号注入的无位置控制[3-4]。前者一般用于中高速范围内的电机控制，后者一般用于低速甚至零速范围内的电机控制。基于反电动势观测的位置观测器有滑模观测器[5-6]、全阶观测器[7-8]、基于扩展卡尔曼滤波观测器[9-10]、基于模型参考自适应(MRAS)观测器[11-12]等。

Romeo Ortega等针对表贴式永磁同步电机提出了一种简单的基于反电动势的非线性位置观测器，并证明了观测器的稳定性[13]，这种观测器易于调整(只有一个系数)，且对电机参数不敏感，但这种观测器只适用于表贴式永磁同步电机[14]。由于IPMSM的直轴电感和交轴电感不相等，在电机凸极率较低的情况下，Ortega观测器将有较大的误差，但当电机的凸极率很大时，角度的估计误差将使观测器不再可靠。之后，文献[15]对该观测器进行了改进，通过合并角度的方式改进电感矩阵，并将改进的电感矩阵代入到原有的非线性观测器方程中，这样就可以获得IPMSM的转子位置信息。但改进的电感矩阵太过复杂，同时需要在每个控制周期内进行更新，不利于计算。文献[16]应用高通滤波器将有效通量转换为新的线性回归形式，从而使改进的观测器能获得IPMSM的位置信息，但是观测器方程仍然非常复杂。

本文基于等效磁链对Ortega观测器进行了改进，使之能运用到IPMSM上，改进后的观测器方程简洁直观，且只有一个可调整系数(观测器放大系数)。

首先，基于IPMSM的电压磁链方程的等效磁链形式，建立了改进的观测器方程，分析了该观测器的稳定性，进而用锁相环得到了电机的速度。然后，在仿真平台对该改进观测器进行了仿真。最后，在相应实验平台上对利用该观测器的无位置控制策略进行了实验验证。

1 IPMSM的改进Ortega观测器

1.1 改进Ortega观测器方程

图1展示了一个简化的三相IPMSM的驱动系统原理图。图1中的驱动器为一个三相电压源逆变器，其由6路开关信号C1～C6控制。

图1 三相IPMSM驱动系统原理图

一般的，永磁同步电机(以下简称PMSM)在α，β静止轴的电压磁链方程可以表示：

(1)

(2)

式中:uαβ为α轴和β轴的定子电压矢量；iαβ为α轴和β轴的定子电流矢量；p为微分算子；Ls(θ)为电感矩阵；L0=(Ld+Lq)/2为均值电感；ΔL=(Ld-Lq)/2为差值电感；Rs为定子相电阻；Ld和Lq分别为d轴和q轴的电感；ψf为永磁磁链。

根据式(1)、式(2)，不难得到如下形式的电压磁链方程：

(3)

将其进一步化简，可以得到:

(4)

令等效磁链ψm=ψf+(Ld-Lq)id，有:

(5)

这样就得到了IPMSM在α，β轴上的基于等效磁链的电压磁链方程。

为了得到改进Ortega观测器，首先定义一个新的状态变量：

(6)

令:

y=uαβ-Rsiαβ

(7)

则可以知道y不包含未知项，根据式(5)，有:

(8)

为了建立观测器方程，定义一个矢量函数η:2→2如下：

(9)

根据式(9)，可以知道：

(10)

由此建立观测器：

(11)

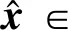
首先，由式(11)可以知道：

(12)

因此定义：

(13)

由此得到观测到的位置：

(14)

1.2 稳定性分析

(15)

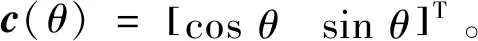
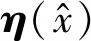
文化复兴已成为国家战略，荥经黑砂独特的文化品牌又一次迎来新的重大机遇。“一带一路”等战略的提出，我国与沿线国家在文化领域合作不断深入，黑砂文化将走出国门，成为雅安、中国的名片。同时，在雅安市委、市政府也大力支持黑砂文化的保护与传承，除了与美术院校开展合作，引进创意人才外，还积极编制“中国黑砂”城总体规划，提出“以黑砂产业为核心，多元融合，创新发展”，打响“中国黑砂”品牌，以品牌效应带动全域旅游，实现文旅深度融合发展，把荥经建设成为特色旅游目的地。

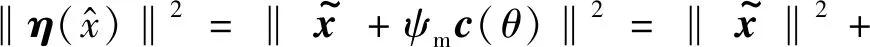
(16)

因此，等效磁链的估计误差可以表示：

(17)

其中:

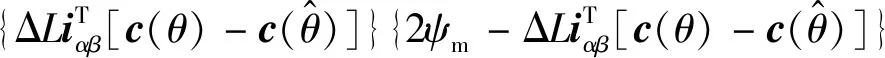
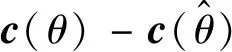
(18)

(19)

(20)

结合上述变换和式(13)中c(θ)的定义，不难得到以下等式：

(21)

(22)

1.3 速度观测原理

为了得到转速，实现速度的闭环控制，可以将观测所得的位置信息作为输入，利用锁相环来得到转子的速度，如图2所示。

图2 速度观测原理图

其方程:

(23)

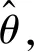
2 系统仿真分析

仿真系统的结构如图3所示。在每个控制周期，采样三相电流并将其转换到α，β坐标系，然后将iα和iβ以及uα和uβ输入到观测器，观测器和锁相环将计算出用于控制的电角度和速度。利用MATLAB/Simulink搭建仿真模型，仿真用IPMSM参数如表1所示。

图3 改进观测器的IPMSM无位置传感器控制系统结构

表1 仿真用IPMSM及控制系统参数

图4分别展示了电机在速度指令和负载转矩交替变化时的估计电角度和估计误差、实际速度和估计速度和速度设定值以及负载转矩和电磁转矩的波形。观测器放大系数设置为2 000，同时考虑到当电机起动时电机转速不高，此时观测器的输出角度不可靠，所以在电机起动前0.1 s，FOC使用角度是实际的位置信息，在0.1 s之后才使用观测器输出的电角度。在0.4 s时，设定转速由400 r/min下降至250 r/min，在0.6 s时，负载转矩由6 N·m突然上升至10 N·m，可以看到，电机的速度观测值始终跟随速度设定值以及实际速度，且观测值与实际值的偏差很小，但观测值会略微滞后实际值，这可以从图4(b)看出。同时，当速度运行在一个稳定点时，如0.3 s～0.4 s或0.8 s～1.0 s，电机的电磁转矩会在实际负载转矩附近小幅波动，在电机速度指令突然变化时，负载转矩会有剧烈的变化。根据图4(a)可以看出，在0.1 s～1.0 s整个过程中，观测器输出的观测电角度都能较好地跟随电角度实际值，且两者的误差在-15°～ 15°以内，在高速情况下观测器的误差范围会比低速情况下更小，这和观测器是基于反电动势有关。同时，当电机的转速和转矩发生突变时，观测器仍能输出可靠的电角度估计值，这也证明了观测器的鲁棒性。

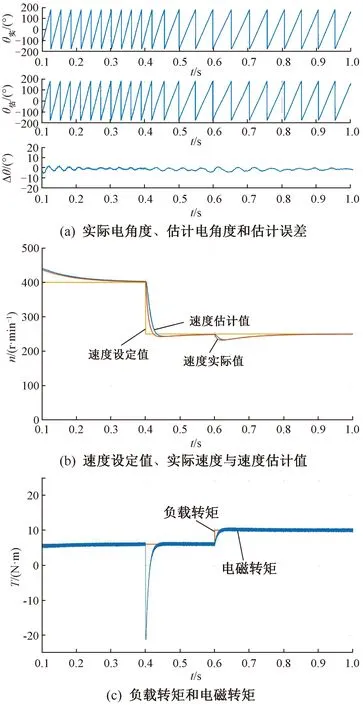
图4 速度与转矩交替变化下的仿真结果

本文的观测器是在文献[13]中针对表贴式PMSM观测器的改进，在电机凸极率不高的情况下，使用Lq作为原观测器的电感参数，使用原Ortega观测器对电角度进行观测。为了验证改进效果，设计了如下仿真实验，将文献[13]中的观测器用于IPMSM，与本文的观测器进行比较，使用观测误差绝对值对时间的积分来直观地表现观测效果。在控制周期中使用的角度是电机的实际电角度。对比如图5所示，图5(a)是原有观测器观测误差绝对值的积分与实际观测误差，图5(b)是改进观测器的实际观测误差。可以看出，改进观测器能更快到达稳定，且其在稳定点的观测误差范围也更小；同时，从两个观测器观测误差绝对值的积分来看，改进的Ortega观测器积分值始终小于原有观测器，这说明其整体的观测效果也要好于原有的观测器。这意味着基于等效磁链改进的观测器已经能适用于IPMSM，且相较于原观测器，有着更好的观测效果。

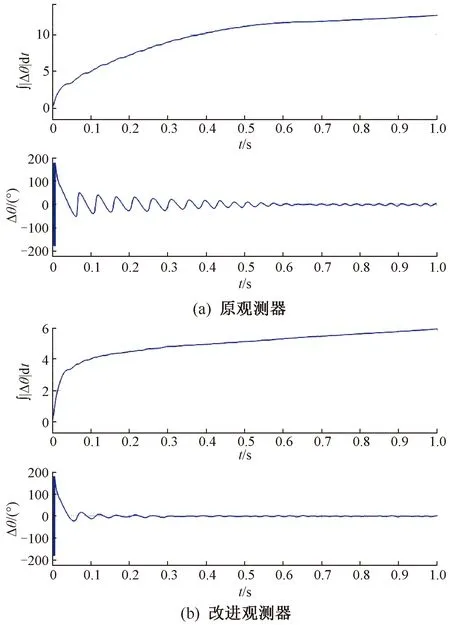
图5 观测误差绝对值的积分与观测误差仿真结果

3 样机实验及结果分析

实验平台包括测试电机和负载电机以及基于DSP芯片TMS32F28335的驱动控制板和16位DAC模块，如图6所示。DAC模块用以输出观测与实际的电角度以及估计与实际的速度等信号波形。测试电机的参数和仿真参数一致。

图6 实验平台

图7展示了电机运行在空载稳定速度时的估计电角度、实际电角度以及观测器状态变量的波形。这4个波形全部由DAC模块输出。电机在控制时使用的角度是实际电角度，电机转速为180 r/min。可以看到，观测器输出的估计电角度能较好地跟随实际电角度，同时观测器的状态变量也能以一个恒定的幅度作正弦振荡。电机电角度的估计误差由示波器内置函数计算得到，即实际电角度减去估计电角度。由于观测器输出的角度相对实际电角度有稍许的相移，所以在0和360°切换时估计误差会有稍许的脉冲，脉冲高度接近360°，此时的误差也可以认为很小，估计误差在观测器未并入FOC中时始终很小，观测器都有良好的观测效果。

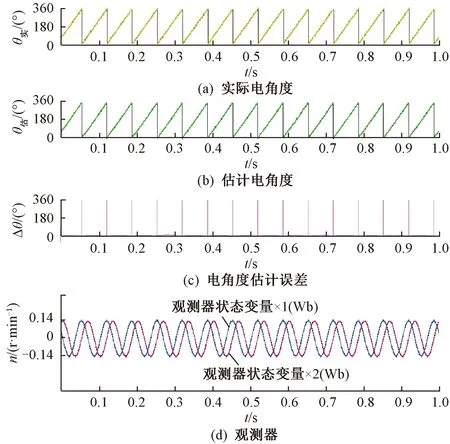
图7 空载180 r/min下的电角度与观测器状态变量波形

图8展示了速度缓慢变化情况下的估计电角度、估计误差、速度设定点以及速度观测值的波形。估计误差也是由DAC模块获取，同时被限制在-180°到180°之间，FOC使用的位置以及速度分别是由观测器以及PLL输出。速度设定值在0.4 s到1.4 s时由180 r/min平缓上升至300 r/min，可以看到，锁相环输出的速度估计值能跟随速度设定值的改变而改变，但会相对有所滞后，同时在整个过程中，位置的估计误差始终在5°以内。当电机的速度发生改变时，该观测器有着良好的动态响应，也能维持优秀的观测效果。当速度提升时，估计误差也会随之略有减小，观测误差的大小和电机转速有着一定的关系，转速越大，观测器的估计误差也会越小。

图8 速度缓慢改变下的估计电角度与估计误差以及转速波形

图9展示了电机在负载转矩变化时的A相电流，估计电角度误差，速度设定点以及速度观测值的波形。速度设定值为180 r/min。在0到0.6 s，电机运行在空载状态，在0.6 s到4.0 s，会有一个负载转矩施加在电机上，此后电机又回到空载状态。在负载转矩增大时，A相电流幅值会增大，速度会有所下降，但很快能回到速度设定点，速度下降时观测器的估计误差也会随之上升，当速度回到参考点时，电角度的估计误差也会回到一个较小的值。当移除负载转矩时，电机的转速又会短暂的上升并很快回到参考值，同时观测器的估计误差也会变得更小。在这一过程中，观测器的误差始终很小，在转矩变化时，观测器能始终稳定跟随实际的电角度。

图9 转矩变化下的波形速度以及角度估计误差的波形

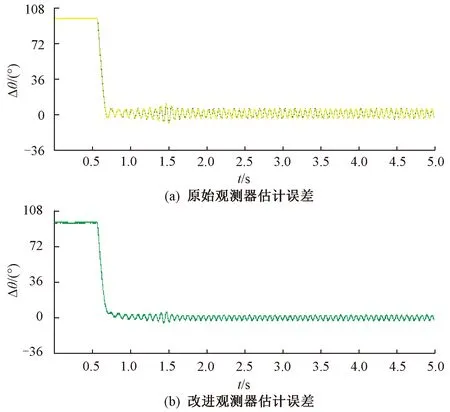
图10 原始观测器和改进观测器输出电角度的估计误差

4 结 语

本文提出了基于等效磁链改进的Ortega观测器，并基于此非线性观测器所观测到的转子位置信息，建立了IPMSM的无位置传感器控制系统，利用MATLAB/Simulink对该观测器进行了仿真验证，对各种工况下的无位置传感器控制系统进行了相应的分析，最后利用基于TMS320F28335芯片搭建的实验平台，测试了各种工况下实验样机的运行情况，验证了改进Ortega观测器的有效性和可行性。