一类二阶差分方程边值问题的正解
张 政,柏仕坤,彭 皓
重庆师范大学数学科学学院,重庆,401331
随着医学、 生物数学、 经济学和现代物理及化学等学科领域的快速发展,大量由差分方程描述的数学模型被提出和研究, 例如: 复利的计算、 还款数量的确定、 经济效益的评估、概率的递推关系和种群数量变化的描述等。 近年来,有很多学者致力于差分方程(组)边值问题解的存在性及其性质研究,参见文献[1-7]。特别地,在文献[1]中作者运用锥上的不动点指数研究了二阶差分离散周期边值问题,获得了正解的存在的最优条件。在文献[2]中作者运用Leray-Schauder不动点定理,在权函数允许变号的情形下,讨论了二阶差分Dirichlet边值问题正解的存在性。
受上述文献的启发,本文研究如下二阶差分方程边值问题正解的存在性:
(1)
其中,Δu(k)=u(k+1)-u(k),Δ2=Δ(Δu(k))=u(k+2)-2u(k+1)+u(k),T1={1,2,…,T},并且非线性项f满足条件:
(H0)f∈C(T1×R+,R+)(R+:=[0,∞));
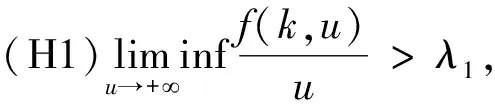
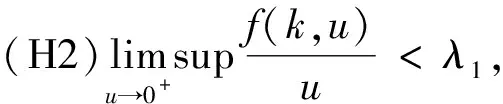
对k∈T2一致成立;
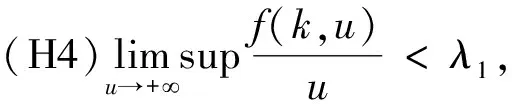
(2)
通过运用不动点指数的缺方向性和同伦不变性,在相关算子第一特征值条件下获得问题(1)正解的存在性,推广和改进了近期这方面的一些成果。
1 预备知识
引理1边值问题(1)等价于[4]

(3)
其中
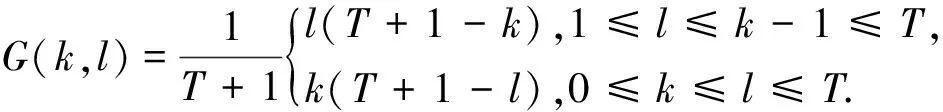
G(k,l)>0,G(k,l)=G(l,k),k,l∈T1,

(4)
则根据(H0)和G知A:P→P,且问题(1)正解的存在性等价于算子A正不动点的存在性。因此,转而研究算子A正不动点的存在性。

证明注意到u(0)=u(T+1)=0,G(0,l)=G(T+1,l)=0,由引理1(ii)知:
从而有
证毕。
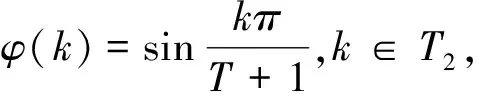
(5)

(6)
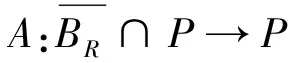

2 主要结论
令引理4和引理5中的有界开集为Bρ={u∈P:||u||<ρ},ρ>0。
定理1若(H0)-(H2)成立,则(1)至少有一个正解。
证明根据条件(H1),存在ε>0,C1>0使得:
f(k,u(k))≥(λ1+ε1)u(k)-C1, ∀k∈T2,u∈R+。
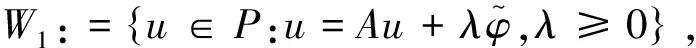
在上式两边同乘φ(k),然后再对其求和,由式(6)得到:
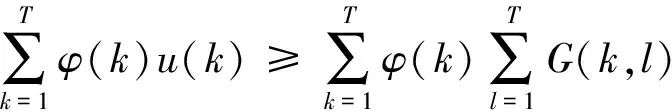
[(λ1+ε1)u(l)-C1]
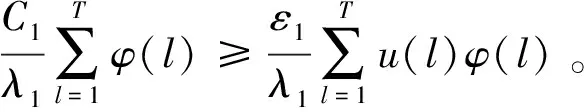
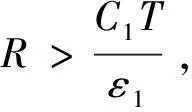
(7)
根据引理4知:
i(A,BR∩P,P)=0
(8)
另一方面,由条件(H2)知,存在0 f(k,u(k))≤(λ1-ε2)u(k), ∀k∈T2,0≤u≤r 下证 (9) 若(9)不成立,则存在u1∈∂Br∩P和λ1∈[0,1],使得λ1Au1=u1。因此 u1(k)≤(Au1)(k) 在上式两边同乘φ(k),再对其求和,由式(6)得到: 由引理5知: i(A,Br∩P,P)=1 (10) 根据式(8)和(10)可以得到: 因此边值问题(1)至少有一个正解。证毕。 定理2若(H0)(H3)(H4)成立,则边值问题至少有一个正解。 证明由条件(H3)知,存在ε3>0和r>0使得f(k,u(k))≥(λ1+ε3)u(k),k∈T2,u∈[0,r]。 从而有: (11) 下证。 u-Au≠λφ,∀u∈∂Br∩P,λ≥0 (12) 若(12)不成立,则存在u2∈∂Br∩P,λ2≥0使得u2-Au2=λ2φ。由式(11)可得 上述方程两端同时乘以φ(k),然后再对其求和,由式(6)得到: 故u2(k)≡0,∀k∈T1,这与u2∈∂Br∩P矛盾,因此(12)成立。根据引理4知: i(A,Br∩P,P)=0 (13) 另一方面,由条件(H4)知存在ε4∈(0,λ1),C2>0使得 f(k,u(k))≤(λ1-ε4)u+C2,∀u≥0,k∈T2 (14) 令W2={u∈P:u=λAu,0≤λ≤1},下证W2有界。 若u∈W2,由式(14)得到: 上述方程两端同时乘以φ(k),然后再对其求和,由式(6)得到: 解上述不等式可得: 注意到u∈W2和引理2知u∈P0,从而有 u≠λAu,∀u∈∂BR∩P,λ∈[0,1] 根据引理5知: i(A,BR∩P,P)=1 (15) 结合(13)和(15)得到: 因此边值问题(1)至少有一个解。 差分方程由于其自身的特点给研究造成了一定的困难,对于现实世界来说离散化或者问题提出时便是离散的差分方程是不可避免的,因此研究该类方程具有一定的现实意义。本文在相关算子第一特征值条件下研究二阶差分方程边值问题(1)正解的存在性。首先将其转化为等价的和分方程,构建算子方程,然后运用不动点指数理论研究算子不动点的存在性,进而获得原问题正解的存在性。本文使用的条件是研究该类问题的最优条件。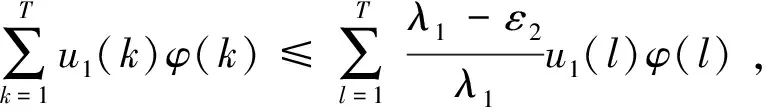
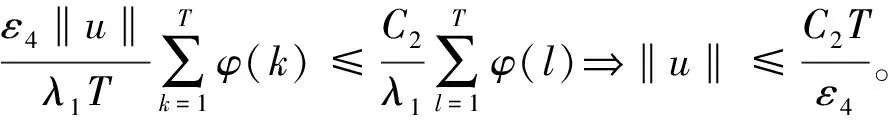
3 结 语

