一种识别PSK与QAM调制信号的改进方法*

杨 栋，张 晔，熊 刚

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

随着无线通信技术的快速发展，人们对信号的监测和调制自动识别技术要求更高，使得调制信号分类识别的作用越来越重要。由于网络电磁空间环境中噪声和干扰日益增加且信号类型复杂多样，因此调制自动识别的方法需要不断发展。各国的研究人员和学者开展了对调制自动识别新思路的探索。据报道，2018 年美国陆军举办了信号分类识别挑战赛活动。参赛队伍要利用大量无线电信号作为数据，开发出先进算法实现信号分类，希望实现电磁频谱战中信号的快速分选和识别。美国国防先期研究计划 局（Defense Advanced Research Projects Agency，DARPA）还资助了一个名为“调制识别之战”的项目，旨在开发可识别信号来源和类型的新的调制自动识别技术，以挖掘在无线电“波形丛林”更多的信号情报潜力。此外，调制自动识别也在信号确认、非法用户检测等民用领域中有广泛应用[1]。

通信信号的调制自动识别一般可分为类间识别和类内识别两种。类间识别是指对不同调制样式的识别。本文以典型采用的不同阶数PSK 和QAM 类型区分识别为典型目标对象开展研究分析。类内识别是指对调制样式相同而调制阶数不同信号的区分识别。例如，4PSK 和8PSK 或者16QAM 和64QAM的判别。信号调制自动识别问题实质上可视作一种典型的模式识别问题，其基本任务是正确地实现对信号调制样式的归类识别。调制自动识别的重要步骤通常包括预处理、特征提取和分类识别。其中：预处理可以起到为后续输入合适的信号数据的作用，一般需要经过正交变频、滤波去噪等环节；特征提取是对信号进行有效的时域、频域或其他变换，从而提取出准确的调制特征；分类识别能够根据参数特征及合理规则实现对调制信号的判决、归类。分类识别的处理基本流程，如图1 所示。

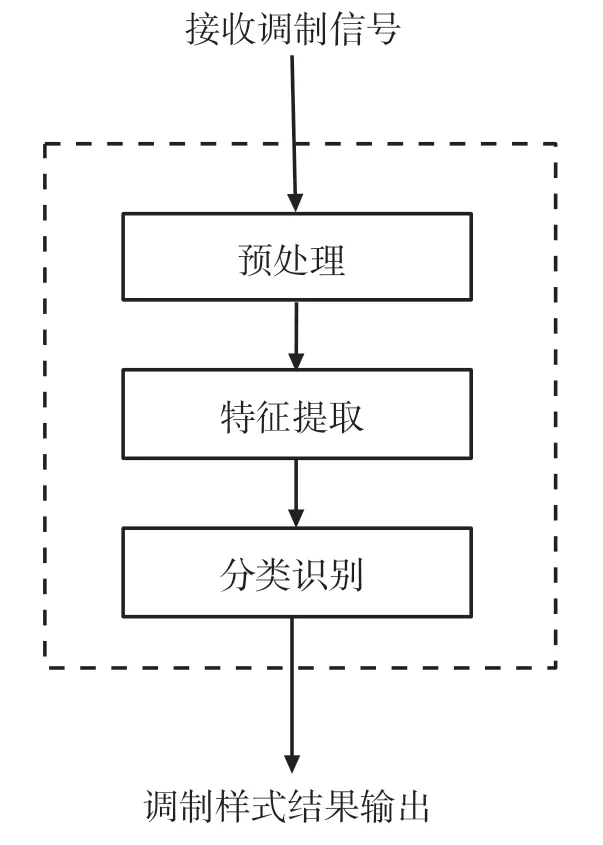
图1 信号分类识别的处理基本流程

对于非协作接收系统，对调制信号类型的有效识别也是后续进行解调分析的基础。由于调制自动识别的重要性，一些学者和技术人员对其不断关注，并开展了有关方法的研究，尤其是对采取高阶调制样式的通信信号如何更好地识别问题，逐渐成为热点和难点。调制自动识别常见思路包括有基于似然的识别思路、基于特征的识别思路等。例如，在文献[2]中使用了一种最大似然判决的调制自动识别算法，可在理想环境中进行分类识别，缺点是对高阶调制信号模型的鲁棒性较差，且容易受到相位和频率偏移、剩余信道效应、定时误差等因素的影响。文献[3]提出了一种基于熵和海林格距离的识别思路，用以寻找分类的最佳匹配模板，但需要积累大量的数据样本，且在有相位抖动的情况下无法很好地适应。

针对上述问题，此处提出了一种基于改进的高阶累积量和决策树的高阶调制信号识别方法。新算法在对高阶PSK 调制、PAM 调制和QAM 调制信号的特征提取过程中采用了混合累积量提高鲁棒性，并根据对最佳逼近阈值的推导计算实现调制分类决策树的优化，不仅能够准确对通信调制信号进行类间识别，还可高效地实现类内识别。分类器采取的统计信息可以通过递归处理实现更新。该方法抗噪性强，且对频偏、相位抖动等因素的影响不敏感，也能用于非高斯噪声环境，便于工程实现。该方法的适应性较好，可正确识别多种典型的高阶数字调制信号。

1 信号模型分析

接收端在采样和预处理后得到基带数字信号，其包络为复数包络的形式。信号频偏与定时误差可通过跟踪环路实现精确估计，减少了基带残余效应影响[4]。

待识别信号的模型表达式为：

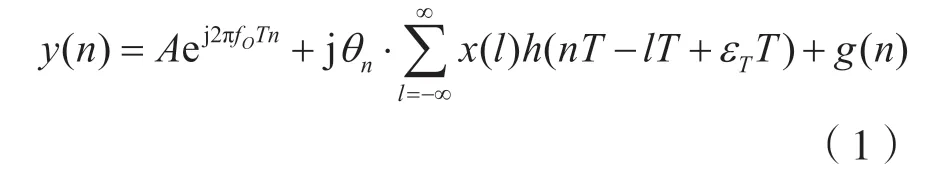
式中：x(l)表示基带传输信号的符号序列；A代表信号包络幅度；T表示符号持续时间；εT（0 ≤εT≤1）表示定时误差；fO表示剩余载频分量；θn表示相位抖动；g(n)代表加性高斯白噪声。fO是序列对应的常量，而θn可视作不同接收符号对应的随机变量。

高阶调制信号通常是相对于低阶调制而言的。信号调制方式将符号码元映射成不同的幅度、相位、频率以及幅度-相位联合的样式。高阶调制一般对应4 阶以上的PSK、QAM 等。由于高阶调制可带来较好的频谱效率，在良好的信道环境条件中，可选择高阶调制样式增加信息传输速率[5]。假设在高阶调制信号的识别过程中存在N种待识别的调制方式，构成集合V={H1,…,HN}，集合里的N种假设对应N个观测矢量(X|Hi),i=1,…,N以及N个不同的概率密度函数p(X|Hi),i=1,…,M，且观测空间可被划分为M个决策域。由于信号识别也可以视作多元假设检验的模型问题[6]，因此可得出如下表达形式：

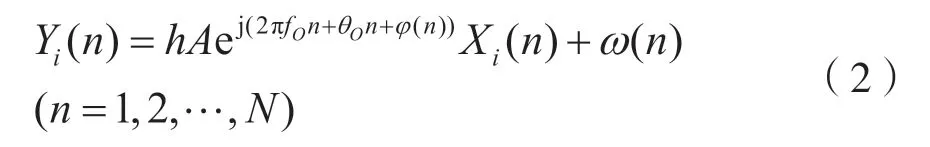
式中：h表示信道响应因子；A表示幅度；Xi(n)表示第i种待识别的调制信号中第n个发送符号；Yi(n)表示接收端中第n个接收到的符号。

可以进一步得出，当待判定的假设为Hi时，相应的识别决策概率的表达式为：

2 识别分类方法分析

信号的高阶累积量特征具有良好的抗噪性，且在一定程度上可以反映出高阶调制星座信号的统计分布状态，如信号的4 阶累积量特征的稳定度较好，下面进行分析说明。

设y(n)表示复数随机过程，根据共轭的位置，二阶矩可以用两种不同的方式定义：

类似地，四阶矩和累积量也可用以下3 种不同的形式表达，因此得到：

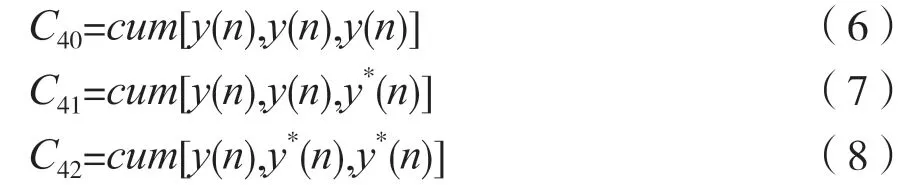
式中，cum表示对信号变量求取高阶累积量的运算符号。

设w、x、y和z表示零均值随机变量，则其对应的联合4 阶累积量的计算表达式为：

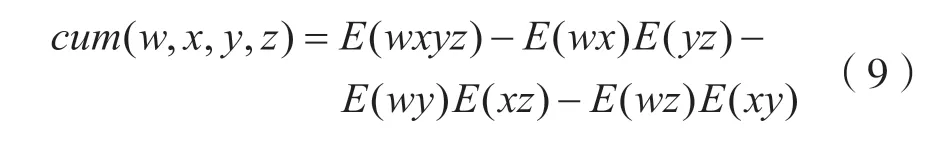
同理地，可进一步得出信号的联合4 阶累积量的切片表达式：

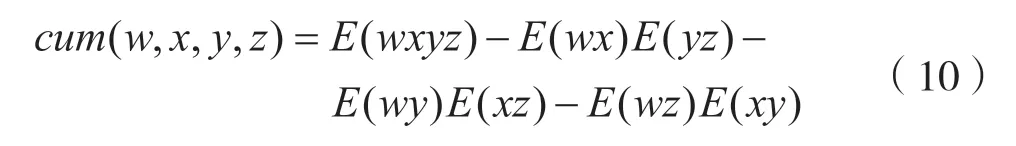
对于经过高斯噪声信道的信号S(t)，其相应的4阶累积量切片表达式为：

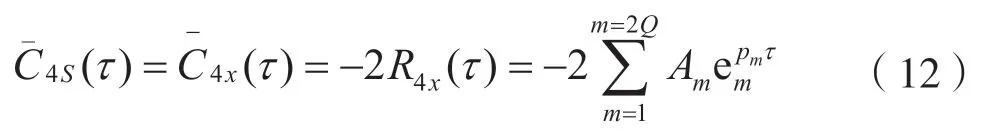
对于相应的矩特征参数，可以根据式（2）和式（3）中的信号高阶累积量进行估计提取。设y(n)的均值为零，在实际处理过程中可通过信号随机变量减去样本均值来实现[7]。信号样本的相关估计能够由式（13）和式（14）得到：

式中，∧表示信号样本的平均变量。

下面给出高阶估计表达式：

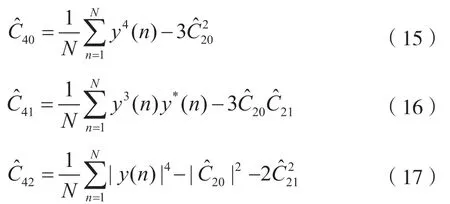
不失一般性，将信号特征参数进行归一化，即有C21=1。在实际处理中，对归一化的累积量特征进行估计，可得：

假设接收符号是等概率的，则表1 列出了高阶调制信号的累积量理论值及样本特征方差。表1 中说明了C40和C42特征在信噪比0 dB 以上时的典型统计值。PAM(∞)表示PAM(n)当n→∞时的极限值，且PSK(>4)为PSK(n)在调制阶数n>4 时的表达式。表1 的最后3 列是C40和C42的样本估计方差。对于表1 中的复数信号，有C20=0、C41=0，且C42和|C40|的累积量统计值具有不受调制星座图相位旋转误差影响的性质，从而使得提取的识别特征参数稳健性较强。

表1 PSK/QAM/PAM 信号高阶累积量特征典型统计值

在表1 中，按照调制阶数不同，主要包括2 阶、4 阶、高阶相位调制信号几大类型，有BPSK 信号、QPSK 信号、PSK(>4)信号等；脉冲幅度调制信号，有PAM(4)、PAM(8)、PAM(16)等；正交幅度调制信号，有QAM(4)、QAM(8)、QAM(16)等。

信号调制参数通过进行提取计算，可以反映出其不同类型的调制特征信息[8]。图2 为对PSK 和QAM 调制信号的分类识别决策示意图。

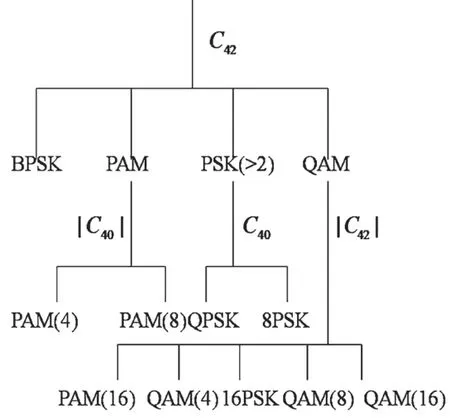
图2 对PSK 和QAM 调制信号分类决策树

图2 实质为一种层次分类的结构。先通过高阶累积量特征C42判断PSK 类信号、QAM 类信号和PAM 类信号，再将计算得到的C40特征用于识别子类的调制信号。这里提出一种优化思路，即当相位旋转偏移量无法忽略不计时，采用|C40|代替C40，从而提高累积量特征在复杂信道中的分类性能，判决区分PSK 子类信号。

还可进一步利用高阶累积量和似然统计提取相结合的思路，实现对PSK 信号的精细分类，由此更大程度地降低噪声的影响，从而增强分类算法的抗噪性能。设T表示调制信号的码元周期，r(t)表示输入到识别算法的接收信号，可得：

式中：c表示统计量的幅度增益因子，为常数；N表示信号采样点的数量。

于是，可得到平方似然统计特征为：

那么可通过似然概率检测的思路达到最小误差概率。当先验条件相同时，即为一个区间检测器，可得出：

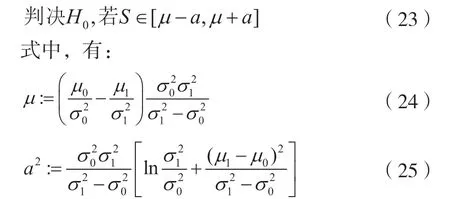
对于二分类问题，总的误差概率可由Q(d/2)得出[9]，其中：

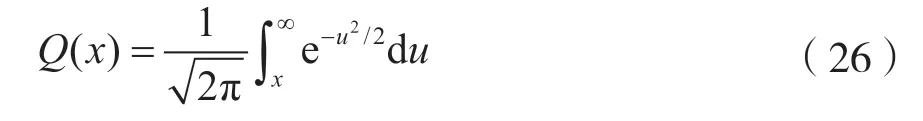
式（26）为标准高斯分布的尾概率函数，且有d=(μ1-μ0)/σ，表示概率空间距离。在等方差条件下，可将先验识别正确概率设为90＆、95＆、99＆，从而得到各自对应的分类方差特征计算结果为3.3σ、3.92σ、5.16σ。通过从表1 得到的数据，可以估计得出待识别信号样本对应的正确分类概率，用Pc表示。

它理论上的概率计算表达式为：

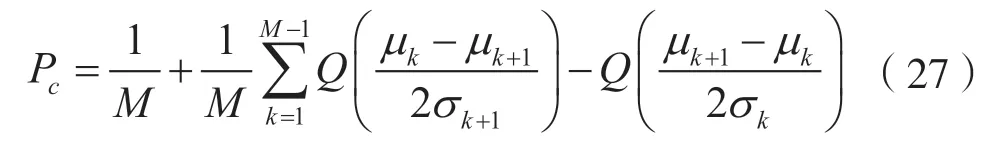
式中，M表示判决的假设条件数量，与待识别的调制信号种类数目相等。

3 仿真分析

设仿真参数如下：接收信号采样率为200 MHz，频率为60 MHz，码元速率为2 Mb/s，样本点数取为8 192，Monte Carlo 仿真次数设为1 000 次，信道噪声为高斯白噪声。图3 为不同信噪比情况下的理论概率Pc曲线示意图，其中横轴表示信噪比（单 位dB），纵轴表示分类概率。

图3 中，N表示接收待识别信号的长度，不同形状的曲线分别对应于N=100、N=250 和N=500 情况下的概率。可以看出，本文方法是一种有效的高阶调制信号分类识别方法，随着样本长度的增加，分类概率达到0.95 所需的信噪比减小，识别性能越来越好。对传统基于谱特征的识别算法和本文中设计的算法进行性能对比仿真，横轴为信噪比，纵轴为平均识别正确率，结果如图4 所示。

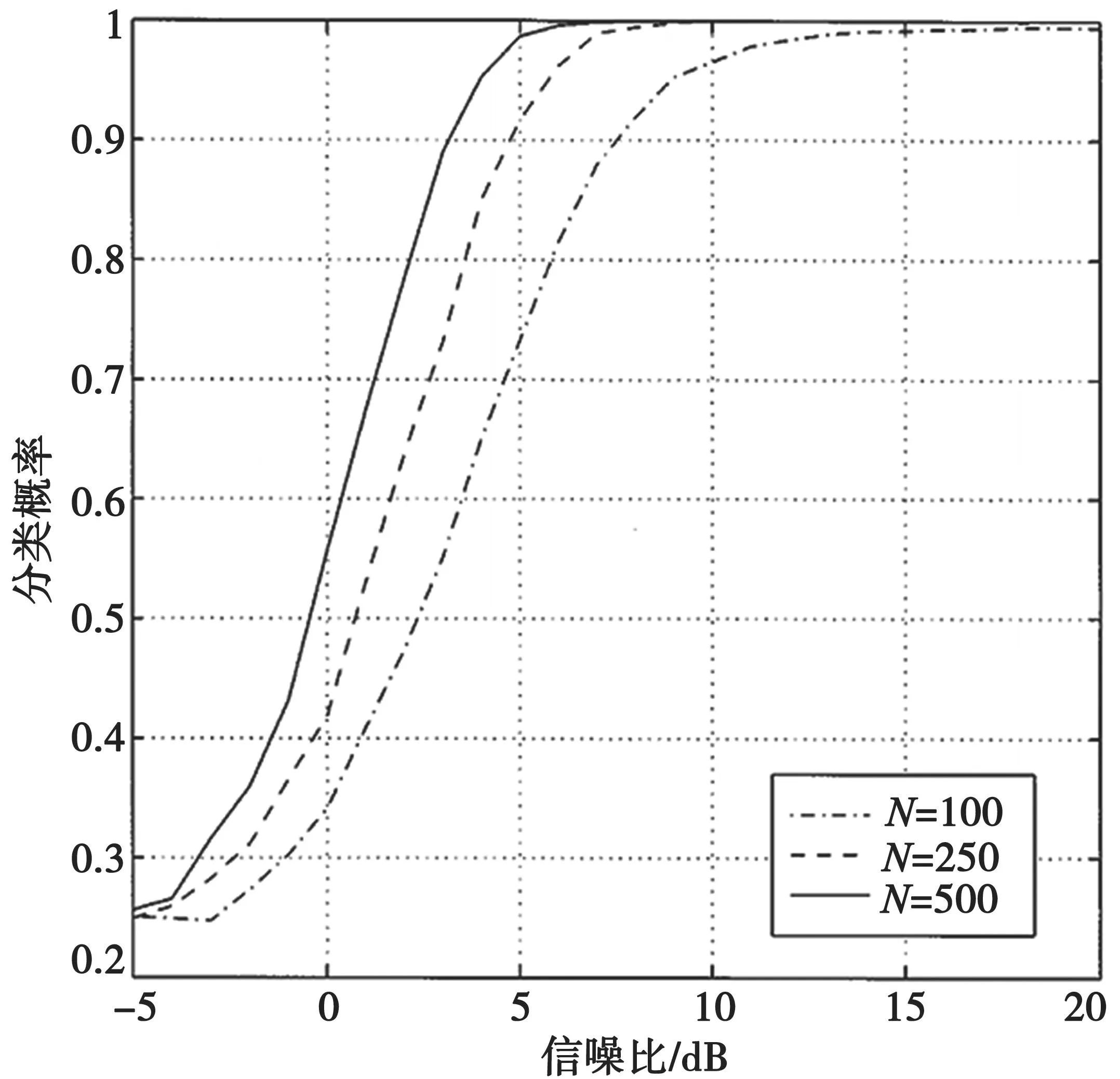
图3 新方法对调制样式的识别率仿真曲线

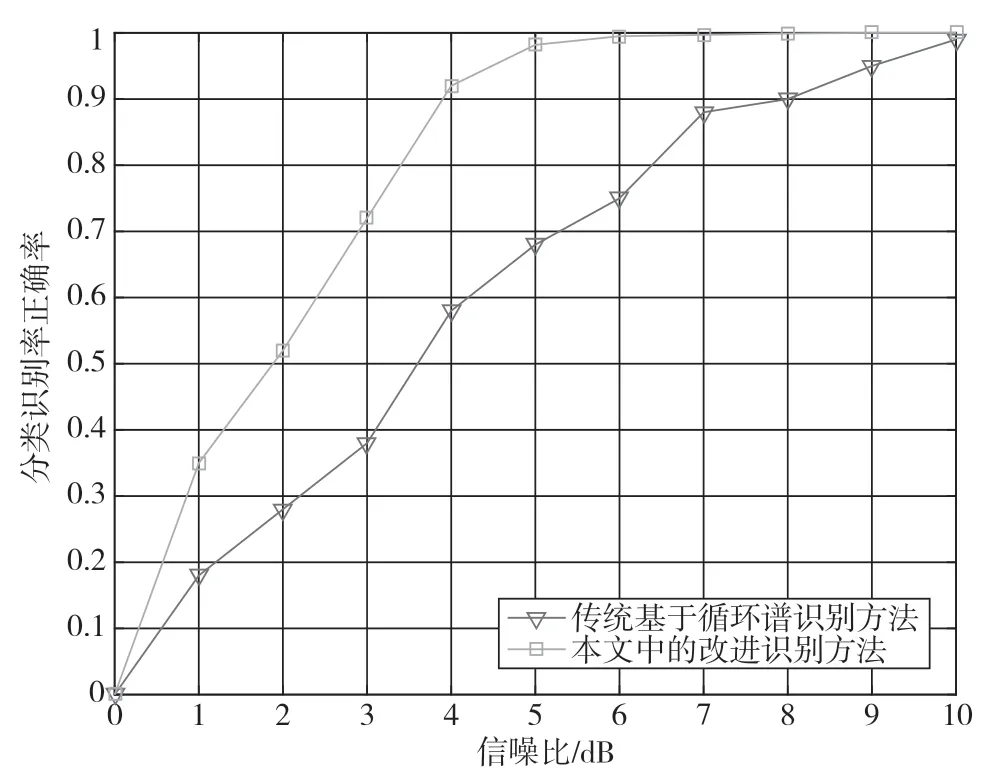
图4 新改进识别方法与传统方法性能仿真曲线

由图4 可得出，新算法相比过去一些调制分类识别方法性能更优。综合前述设计分析，本文中的算法鲁棒性较好，在复杂电磁环境中适用于对PSK和QAM 调制信号的识别。

4 结语

通信技术的进步带来了信号调制类型的更加多样化，分类识别面临的电磁环境也更复杂，因此需要研究和设计新的调制自动识别分类方法以应对目前的挑战，不断改善识别算法的效果。本文提出了一种基于混合高阶累积量和决策树等思路结合的调制分类识别方法。仿真结果表明，该方法识别性能较好，可为解决调制自动识别问题提供一种更有效途径。