基于特征融合的小样本个体识别算法*

王姗姗，王厚钧，程石磊，杨海芬，王小青

（1.中国电子科技集团公司第三十研究所，四川 成都 610000；2.电子科技大学，四川 成都 610054）

0 引言

个体识别技术又称为辐射源“指纹”识别技术，是通过对接收到的信号进行特征提取，然后根据已有的先验信息确定接收到的信号是由哪一个个体产生的。目前，个体识别技术主要有两种——基于人工特征识别和基于神经网络识别。基于人工特征识别主要是人为提取信号载频、脉冲宽度以及杂散特征等人工特征来进行个体识别。这种方式对于不同的个体需要寻找特定的人为特征才能达到较好的准确率，泛化性差，效率较低。基于神经网络识别是运用神经网络自动提取特征并进行识别分类的过程，相比于人工特征，能通过不断训练提取样本特征得到数据丰富的本质信息[1]，拥有更好的泛化性和更高的准确率，因此在个体识别领域得到了广泛应用。

神经网络的训练与学习需要大量有标签数据，如大型数据集ImageNet[2]。但是，在实际应用中，获得的数据集往往难以满足要求，有标签样本数量较少，导致小样本情况下深度神经网络的训练与更新效果不理想[3]。研究小样本条件下的个体识别得到了越来越多研究者的关注，如文献[4]比较了高阶谱加主分量分析降维方法[5]、杂散成分方法[6]及高阶谱稀疏表示方法[7]在小样本情况下的表现，但均不能令人满意。

特征融合能够综合利用多种特征，实现各个特征的优势互补，以获得更加鲁棒与准确的识别结果[8]。文献[9]将双谱融合的准确率与不融合的准确率进行比较，发现融合后准确率有一定程度的提升。

在以上文献研究的基础上，本文将神经网络学习得到的特征与人工提取的特征进行融合，将得到的新特征用于小样本个体识别，并最终仿真验证了提出算法的有效性。

1 系统模型

本文研究的个体识别指通信辐射源个体识别。系统模型如图1 所示。

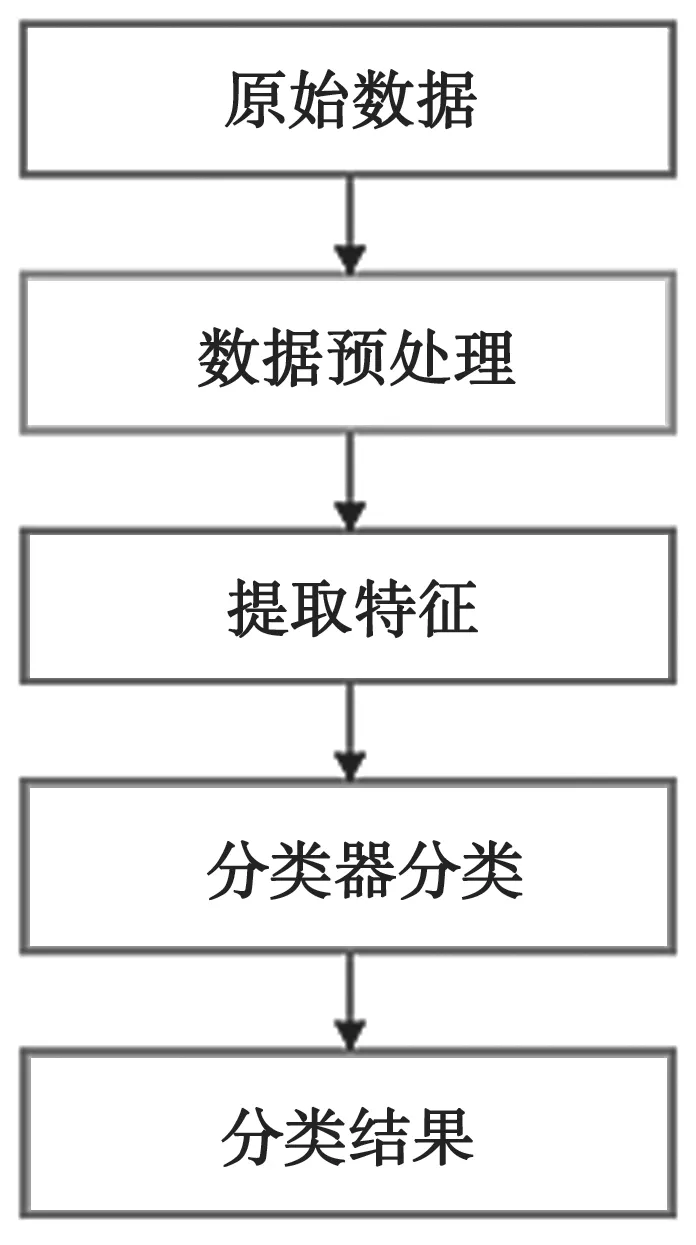
图1 个体识别系统模型

假定有N个个体，原始数据经过预处理提取特征后得到的训练数据集为X={X1,X2,…,XN}，其中Xi是指第i(i=1,2,…,N)类个体的训练数据集。测试数据集为T={T1,T2,…,TN}，其中Ti是指第i(i=1,2,…,N) 类个体的测试数据集。每一类个体均有标签l(xij)=i，其中xij表示第i类个体的第j个数据。训练时使用X训练初始化的分类器，然后将测试集T输入到训练好的分类器模型中得到分类结果。

2 Alexnet 网络

Alexnet 网络的出现极大地推动了深度学习在各领域的应用[10-13]，网络结构如图2 所示。Alexnet模型有8 层需要训练参数，包括5 层卷积层和3 层全连接层。模型中，卷积层是网络提取信号特征的关键结构。信号经过的卷积层越多，提取出的特征越复杂、越有效。全连接层的作用是将经过多层卷积层与池化层后得到的特征图进行处理，将特征图中的特征进行整合，映射成一个特征向量。这个特征向量包含了输入特征的组合信息，保留了特征图中最具有特点的特征。最后，输出层使用softmax函数实现输出。

图2 Alexnet 网络结构

Alexnet 模型拥有更多的卷积层与卷积核数量，能够发现与提取数据更加细微的特征，更好地解释数据，分类效果优于Lenet。同时，由于使用了多块GPU 并行处理，Alexnet 在速度上明显优于VGG[11]、GoogleNet[12]等模型。

3 基于特征融合的个体识别算法

3.1 信息维数

分形理论具有统计意义上的自相似性，可以有效提取信号的细微特征，已经被广泛应用于个体识别领域。分形维数是分形理论的中心概念，可以定量描述分行集的不规则度和复杂度[14]，常用的有Hausdorff 维数、盒维数与信息维数等[15]。信息维数可以反映信号在平面空间上分布的疏密程度，且计算比较简单。本文采用信息维数作为个体识别特征。

设X为Rn中任意一个集合，Xk(k=1,2,…,n)是集合X的一个有限ε方格覆盖。Pk表示X中元素落入Xk中的概率，那么有：

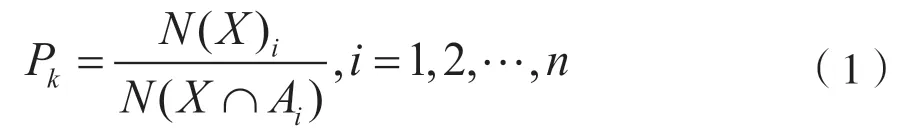
式中，N(Xi)与N(X∩Ai)分别表示元素的个数。于是，信息熵为：

若信息熵满足关系：

那么，信息维数可以表示为：

在实际操作中，采用如下步骤求解包络信息 维数：

AMAROS试验中将1 425例肿瘤直径≤5 cm，且前哨淋巴结有1～2枚转移的病人随机分为行腋窝淋巴结清扫组和行腋窝放疗组[10]，结果发现，两组间无病生存率及总生存率差异无统计学意义(P>0.05)。AMAROS试验表明两种治疗策略均能够提供很好的局部控制效果，但是并没有指出哪部分前哨淋巴结阳性的患者需要进一步处理。

（1）提取通信信号的包络并进行采样，得到信号包络序列s(t)(t=1,2,…,M)，这里M为信号序列的长度；

（2）将包络序列s(t)分段，每段长度为N，分别对每段求信息维数DI；

（3）将信号包络序列按照以下方法进行重构，以减弱部分带内噪声的影响，同时便于计算信息 维数：

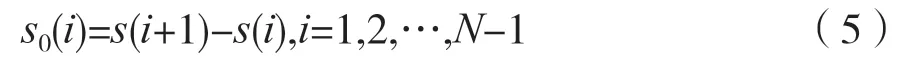
（4）利用重构后的信号包络序列计算信息维数，令：

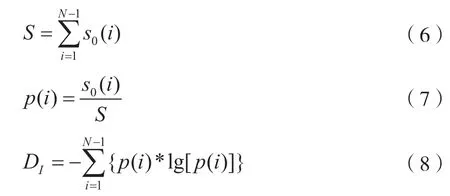
3.2 算法流程

本文提出的基于特征融合的小样本个体识别算法流程如图3 所示。

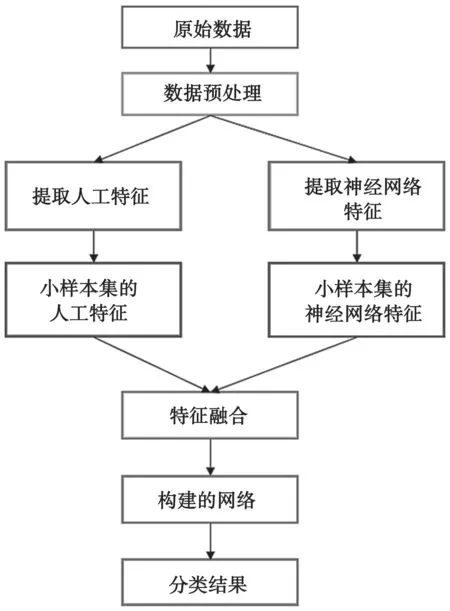
图3 小样本个体识别算法流程

具体实现步骤如下。

（1）对采集的数据做下采样，过滤掉数据中的空白部分。

（2）对得到的信号进行短时傅里叶变换（Short-Term Fourier Transform，STFT），得到信号的功率谱密度P与经过变换后的信号Y。

（3）对Y求希尔伯特变换得到包络，然后根据式（5）～式（8）得到信号的信息维数矩阵D。

（4）从数据中随机选取一部分作为小样本数据集A，将A中数据对应的功率谱密度PA进行归一化。

（5）将PA作为特征导入到Alexnet 模型中进行训练，提取模型中第一个全连接层的输出作为神经网络特征MA。

（6）将A 对应的信息维数矩阵DA与式（5）中得到的MA进行拼接，得到新的特征矩阵Z。

（7）将新的特征矩阵Z归一化后，导入到构建的神经网络中进行分类。

构建的网络模型Net1 结构如图4 所示。Net1包括两个二维卷积层，每个卷积层的卷积核尺寸均为（5，5），在每个卷积层后有一个最大池化层，池化核尺寸为（2，2）。每个池化层后有一个Dropout 层来减少过拟合，Dropout 率设为0.25。

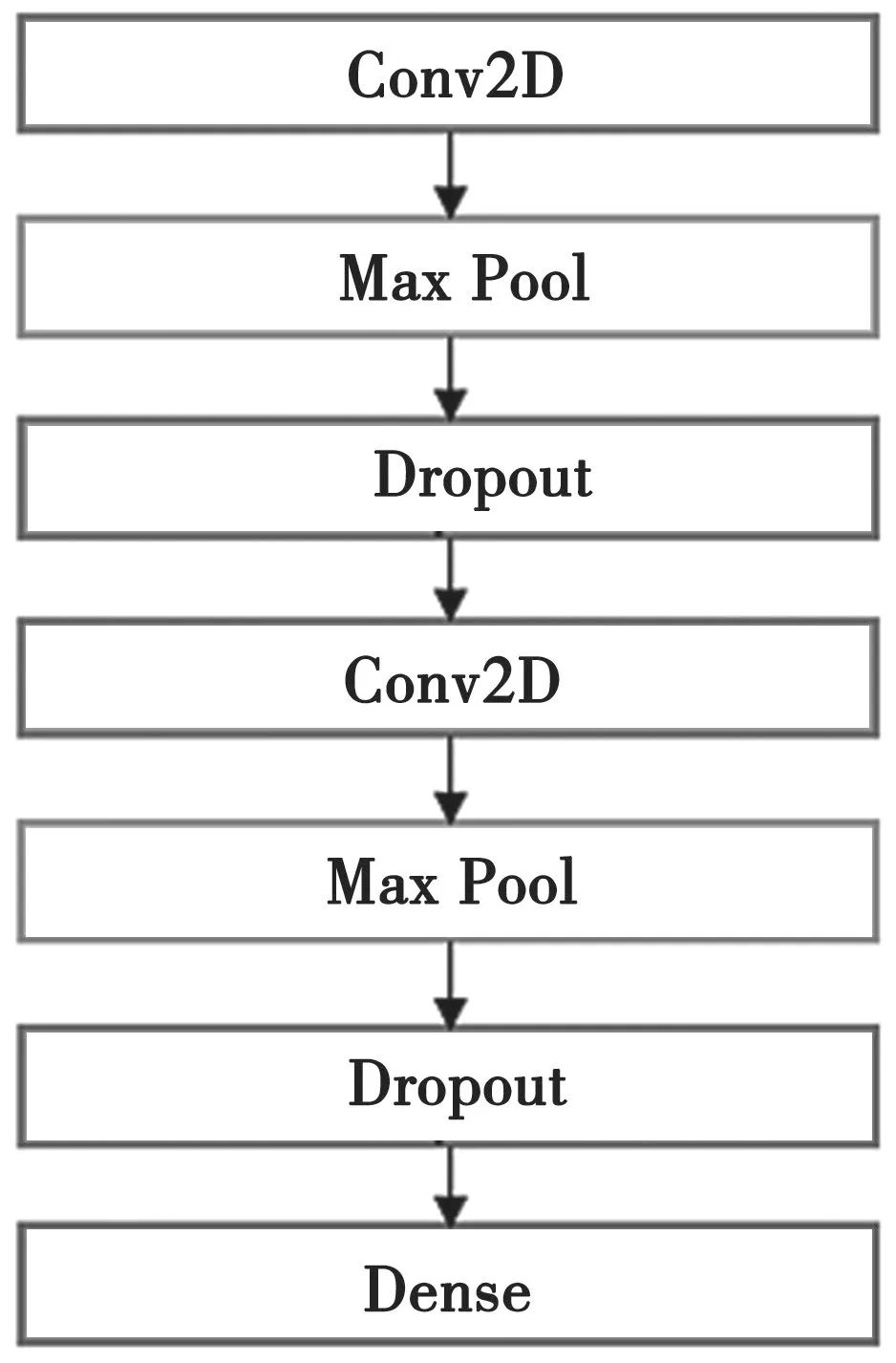
图4 Net1 结构

4 仿真结果

本文采用10 台相同型号的辐射源来产生实验数据，从实验数据中分别随机选取6＆、8＆、10＆、20＆、40＆的数据作为小样本数据集，并使用Alexnet 模型、使用信息维数以及本文提出的算法的准确率进行比较，比较结果如图5 所示。

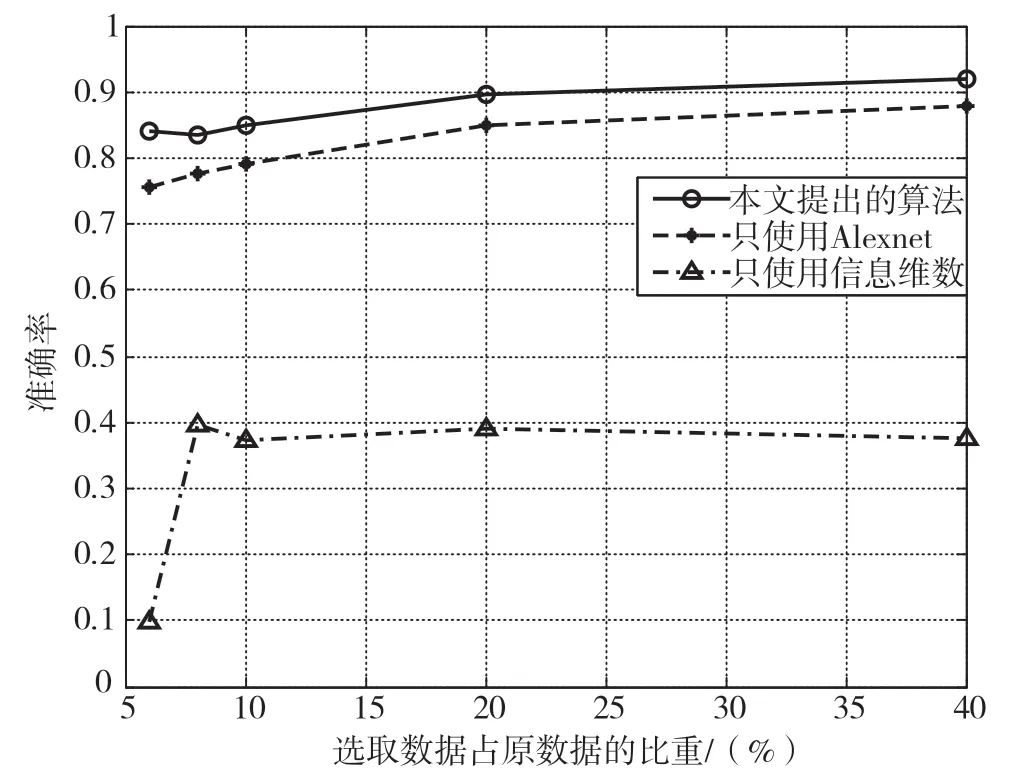
图5 选取不同占比数据3 种方法准确率

通过图5 可以看出，随着选取数据占原数据比重的增大，Alexnet 算法与本文提出算法的识别准确率均逐渐增大，而信息维数算法则会产生波动。当只选取6＆数据做样本时，Alexnet 只有75.7＆的准确率，而提出的算法能将准确率提升到84.1＆。在小样本情况下，只使用信息维数无法正确分类；只使用Alexnet 会导致网络无法进行充分的训练，且准确率不高。本文提出的算法相比Alexnet 至少能提高5＆的准确率，相比只使用信息维数能提高50＆，且在选取原数据20＆的情况下准确率接近90＆，选取原数据40＆的时候准确率超过90＆，能有效识别个体。

实验过程中，当选取40＆数据做小样本集时出现了过拟合现象，混淆矩阵如图6 所示。

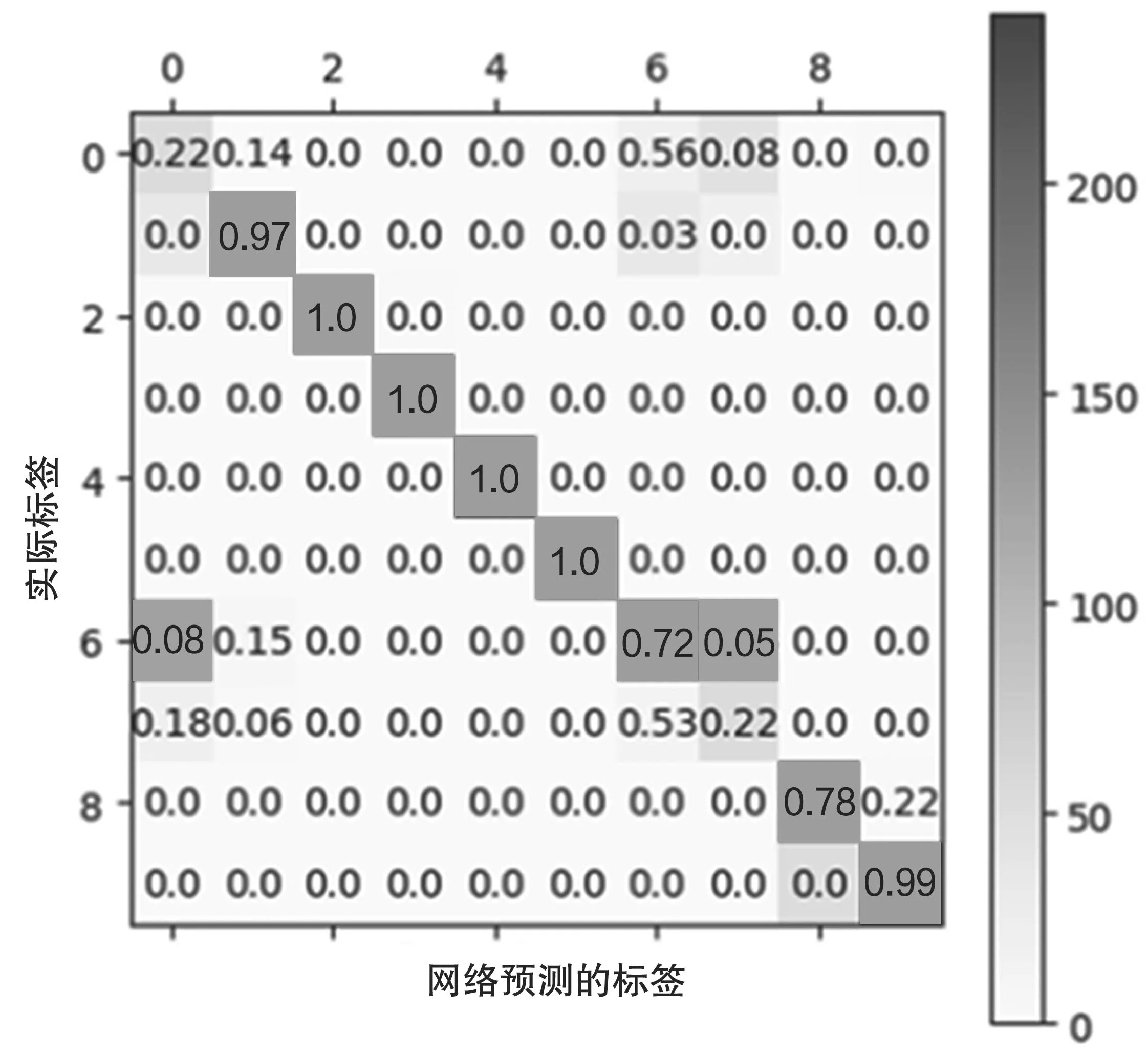
图6 40＆数据的过拟合混淆矩阵

从图6 中可以看出，至少有50＆的第1 类与第8 类的个体被识别为第7 类，有22＆的第9 类个体被识别为第10 类。这是由于第1 类、第7 类与第8 类的信号比较相像，第9 类与第10 类的信号比较相似。由于训练数据不足，导致网络在学习与训练的过程中以牺牲第1 类、第8 类与第10 类的正确率为代价，提高第7 类与第10 类的准确率，产生了过拟合，平均正确率只有79＆，相比于正常情况下降7＆。

对于过拟合的情况，使用本文提出的算法得到的混淆矩阵如图7 所示。

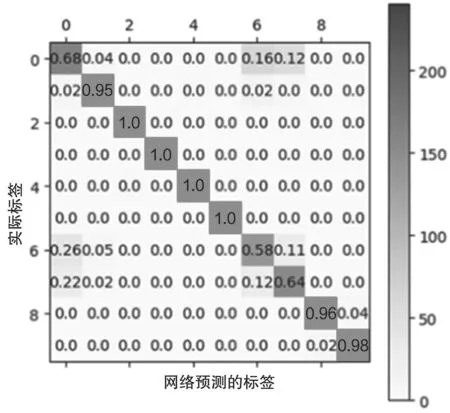
图7 过拟合时采用本文提出算法的混淆矩阵

从图7 可以看出，相比于图6，本文提出的算法能将第1 类与第8 类的准确率提升50＆以上，同时也能将第9 类的识别率提升至96＆。10 项分类的平均准确率能达到87.9＆，相比于Alexnet 能提升8.9＆，说明本文提出的算法能有效恢复因为过拟合而下降的准确率。

5 结语

针对小样本情况下，采用神经网络会因为训练不足而导致准确率下降，且由于训练数据不足可能导致过拟合问题，提出将神经网络提取的特征与人工提取的特征进行融合，将得到的新特征导入构建的网络中进行训练与分类。仿真结果表明，在小样本情况下，本文提出的算法相比只使用Alexnet 能至少提高5＆准确率，且在因训练数据不足发生过拟合时能将准确率恢复到未发生过拟合的情况，充分证明了本文所提算法在小样本情况下的有效性。