舒适服装压及其与织物力学性能相关性研究进展

张宇飞，魏小红，王越平，肖 红

(1.北京服装学院 材料设计与工程学院，北京 100029； 2.军事科学院系统工程研究院 军需工程技术研究所，北京 100010)

人体穿着服装后，无论是静止还是运动状态，都会因服装的压力作用给人体带来舒适或不舒适的服装穿着主观感受，其受到人体生理、心理和服装号型、尺寸及材料等多因素的影响。在实际使用中，一方面，可以通过测量获得人体特定部位或者是特定类型服装的服装压；另一方面，在服装款式、尺寸、应用场景明确条件下，服装压主要来自于织物的物理机械性能，包括弹性模量、拉伸应变及应力等。探明舒适服装压和织物力学性能的相关性，对织物开发及服装设计至关重要。

本文从服装压的定义及分类出发，分析服装压的影响因素，介绍人体不同性别、不同部位和不同类型服装的舒适服装压范围；综述并分析服装压和织物力学性能相关性的理论公式、实际测试等方面的研究进展。提出舒适服装压及织物力学性能相关性的研究方向。

1 服装压及舒适服装压范围

1.1 服装压的概念

服装压指人体穿着服装后，服装对人体表面垂直施加的压力，主要由集束压、面压以及质量压3部分组成[1]。质量压是服装自身质量给予人体的压力，在秋冬季、极地等服装中表现明显。集束压是由于服装宽松量设计较小、系扣绳带或弹性带而产生的压力，这种压力的代表性服装有紧身胸衣、紧身衣裤等。面压是着装者带动服装产生一定的形变导致的内应力，包括剪切应力、弯曲应力、拉伸和收缩应力[2]。人体所受的服装压通常是上述多个力共同作用的结果，实验研究的服装压一般也是三者的统一。

服装压是一个可以量化的数据，常用单位为kPa。服装压的客观评价方法包括直接测量法和间接测量法。直接测量法是在人体和服装之间放置内置空气的橡胶球或气囊，通过内部空气的压缩流动测量服装压[3-4]；或者通过各类压阻/电容/应变/压电/光纤类压力传感器[4-6]，获得特定部位的服装压。为了消除人的主观影响，人们也会使用间接测量法，采用软体假人代替真人进行测试[7-9]。结合实际测量，进一步通过三维人体建模模拟，也可以获得具有一定普适性的人体服装压计算公式[10-11]。

如果穿着的服装能够使得着装者自由运动，减少对肢体的束缚，保持着装者运动舒适，则称该服装具有服装压舒适性，此时的服装压就被称为舒适服装压[12]。通常，舒适服装压并不是一个具体数据，而是一个范围。除了心理、神经生理和生理的人体因素外，人体各部位的物理机械属性及服装性能是关键影响因素。

1.2 不同性别和部位的舒适服装压

影响服装压舒适性的人体客观物理因素主要包括人体各部位的身体曲率、弹性模量、软组织结构、脂肪含量及运动幅度等方面的差异[13-14]。相关研究已经取得了很大的进展，男性女性在人体不同部位的舒适服装压范围[15]见表1。人体不同部位的服装压通常由主观评价法与服装压客观测量法综合得出，统计主观评价为舒适的服装压数值，归纳整理后得出舒适服装压范围。

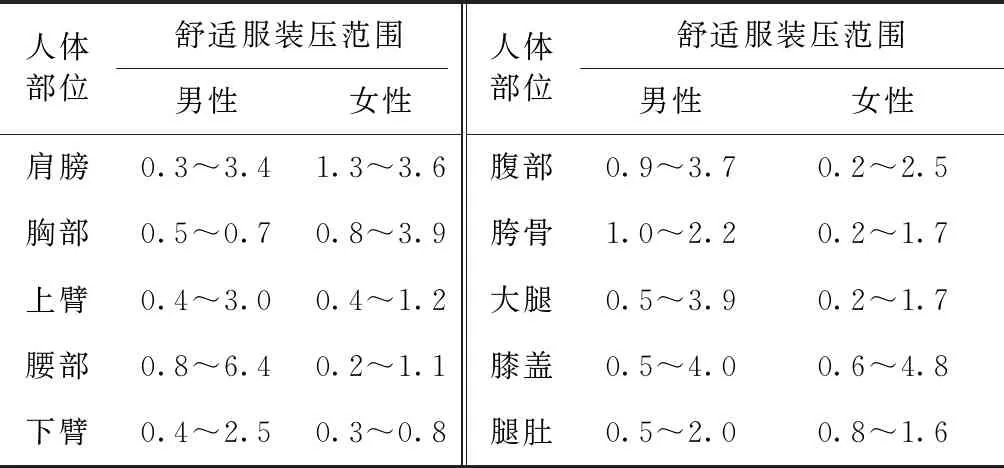
表1 人体不同部位的舒适服装压范围 kPa

由表1可知，在人体多个部位，男性女性相同部位下舒适服装压的范围和最大值均是男性大于女性，比如上臂、腰部、下臂等。但在个别部位，由于男性女性在该部位的曲率半径、表面弹性系数有显著差异，导致舒适服装压有较大差别。一般情况下，曲率半径越小、表面弹性系数越高的部位，其服装压越大[16]。最为典型的部位就是胸部，女性胸部的表面弹性系数更高，曲率半径更小，所以承受的服装压更大，拥有更高的舒适服装压。

1.3 不同服装类型的舒适服装压

影响舒适服装压大小的服装因素主要包括服装尺寸、款式、服装适用对象及场合、构成服装的织物性能等。尺寸越小、款式越紧身，人体感受到的服装压越大。尺寸和款式在服装设计中，通过号型等设置可以调节的服装压，使其处于舒适服装压范畴。

通常根据服装的适用对象及场合，对服装进行分类，对不同类型服装的舒适服装压阈值进行研究，用以指导服装设计。从文献归纳出的不同服装类型对应的舒适服装压范围或阈值见表2。

值得注意的是，表2中的文献获得舒适服装压的方法、具体环境或对象存在差异，本文只是用来说明不同服装类型有不同的舒适服装压范围。研究特定类型服装的舒适服装压，需要针对性的测量和分析。一般情况下，用于治疗增生性瘢痕、血管类疾病的医用长袜的舒适服装压范围略大于用于塑形美体的紧身胸衣、束裤类紧身服装，其服装压均远大于日常穿着的服装。

2 服装压与织物力学性能相关性

对于特定的人体部位，特定的服装款式及尺寸，织物的物理机械性能是影响服装压最关键的因素。根据前人的研究[19, 25-26]可知，有多种织物物理特性都会对服装压产生或多或少的影响，包括织物的拉伸性能、弹性模量、剪切性能、弯曲性能、柔软度以及织物摩擦因数等，其中最为关键的是织物弹性模量及拉伸性能。

表2 不同服装类型对应的舒适服装压范围或阈值 kPa

2.1 理论研究

2.1.1 基于拉普拉斯方程的服装压预测模型

为了探索服装压与织物性能的关系，文献[27]借鉴用于计算固体圆筒容器或弹性容器装满液体后的表面张力的拉普拉斯定律，构建服装压预测模型见式(1)。如Troynikov等[28]通过使包覆圆柱体的织物产生特定的拉力，而后用拉普拉斯定律来预测织物对圆柱体(半径已知)施加的服装压的大小。Maecintyre等[29]进一步验证了拉普拉斯定律的有效性，并证明其在预测曲率半径较小处的服装压时准确程度较低。

P=T/R

(1)

式中：P为圆柱面压力，Pa；T为每米织物的张力,N/m；R为圆柱面的曲率半径,m。

1966年，Kirk等[30]对人体膝盖处的曲率半径和此处的织物拉伸应力进行了测量，提出了织物拉伸应力、身体部位的曲率半径与服装压之间的函数关系式：

P=TH/rH+TV/rV

(2)

式中：P为服装压,Pa；T为拉伸应力,N/m；r为身体部位的曲率半径,m；角标H代表纬向；V代表经向。

在特定情况下，式(2)可以简化为式(3)，进一步说明了服装压与拉伸应力成正比，与身体受压部位的曲率半径成反比[30]：

P=KT/r+C

(3)

式中：P为服装压,Pa；T为拉伸应力,N/m；r为曲率半径,m；K、C为常数。

早期的研究者们基于拉普拉斯方程所构建的服装压预测模型整体较为简单，考虑因素较少，准确程度有待提高。2001年，Ng等[31]在拉普拉斯定律基础上考虑了织物的刚度因素，推导出了服装宽裕量与服装压之间的关系：

(4)

式中：Re为服装宽裕量,%；EI为织物刚度(单位长度的织物张力/织物伸长率),gf/cm；CF为压缩因子；Chuman为人体某部位的周长,cm；P为服装压,mmHg。其中CF是为了使不规则的人体表面与理想圆柱体具有相同的服装压，而使二者织物具有不同尺寸周长所用的转换因子，即压缩因子。

2001年，Ng等[32]研究了管状弹性织物的长宽比对压力服中服装压大小的影响，并发现在给定的弹性织物下，织物施加的服装压与((AR0)/W0-(AR1)/W1)成正比。

(5)

式中：P为服装压,Pa；EI为织物刚度,N/m2；AR0为针织面料拉伸前的长宽比；AR1为针织面料拉伸后的长宽比；W0为针织面料拉伸前的宽度与单位长度的比值；W1为针织面料拉伸后的宽度与单位长度的比值。

Liu等[33]还构建出一种理论模型，该模型可以预测多层的、每层都具有不同拉伸特性的管状弹性织物穿着在圆柱管上时所产生的服装压。当组成多层管状织物的每个织物层的厚度都很小，并且具有相似的应力应变行为时，该模型准确度相对较高。

(6)

式中：P为服装压,Pa；ε为轴向应变,%；C为针织物周长,mm；N为针织物层数；hi为第i层针织物的厚度,mm；Ei为第i层针织物的弹性模量,N/m2。

2.1.2 其他服装压预测模型

1983年，田中道一等[34]考虑到人体和服装间的摩擦因数，提出了公式(7)，描述的是将圆筒状弹性织物包覆在弯曲的肘部或膝部，使弯曲部位产生明显的人体与服装间法向压力。在其余条件相同的情况下，“人体表面—服装”界面摩擦因数越大，所产生的服装压就越小。

(7)

式中：Ps为在任意点S处的服装压, g/cm2；P0为弯曲前的服装压, g/cm2；t0为弯曲处的服装张力,g/cm2；μ为人体表面和服装间的摩擦因数；e为自然对数的底；c、k为常数；s为从弯曲处沿手臂或脚的长度在服装面上测定的距离,cm。

当服装的宽裕量和伸长量小于人体运动状态下的皮肤伸长量时，会引起服装变形拉伸并产生拉伸张力T。2018年，段彩玲[35]提出了理论关系式(8)，建立了服装压与织物的拉伸张力、弹性模量、形变量及人体表面曲率的关系。

F=2Tcosφ=2flcosφ

(8)

式中：F为服装压力,N；T为拉伸张力,N；f为织物弹性模量,N/m2；l为织物形变量,m；φ为织物拉伸张力T与服装压F的夹角。

前述理论公式不约而同的证明了一点：即服装压与织物的力学性能密切相关，存在着定量关系。

2.2 实践研究

2.2.1 定性研究

关于服装压与织物力学性能相关性的定性研究一直在不断发展。Gong等[36]通过测试5种弹性织物伸长率及其不同伸长率下小腿处的服装压，提出织物服装压会随织物伸长率增加而线性增加，并且具有各向异性。Liu等[37]研究了医疗压缩袜(GCSs)的服装压与力学性能之间的关系。服装压较小的GCSs可产生较大的拉伸形变、较低的抗弯刚度和剪切刚度及定负荷拉伸下较好的拉伸性能。而具有更高服装压的GCSs表现出相反的性质。2年后Liu等[38]进一步证明了GCSs的材料性能对服装压的大小及分布有着显著的影响。研究证明了织物的拉伸功(WT)和拉伸应变(EM)与服装压大小呈现明显的负相关性， 剪切刚度(G)和抗弯刚度(B)与服装压大小呈正相关。王伶俐[39]指出，针织物的初始模量、蠕变率、应力松弛率、拉伸伸长率、定伸长力和定伸长功与服装压力呈现显著正相关性，最大弹性伸长率、塑性变形率和定力伸长率与服装压呈现显著负相关性。

可见，进行服装压相关性定性研究的织物力学性能指标，从一开始较为简单的拉伸，逐步加入了剪切、弯曲、弹性等内容，并将初始模量、蠕变率、塑性变形率等也纳入了研究范畴。

2.2.2 定量研究

建立服装压与织物力学性能的定量关系一直是研究者们不懈努力的方向。近些年发展较为迅速的是通过有限元模拟法预测服装压数值。

2011年，Liu等[40]通过有限元模拟法构建了人体胸部的服装压与服装在胸部处的应变、弹性模量之间的关系。首先测量弹性模量、人体穿着弹性运动背心后的服装压，然后构建由皮肤、软组织和骨骼3部分组成的有着标准女性胸部横截面的有限元模型，最后将实测服装压作为载荷代入有限元模拟中，通过有限元模型获得该服装压下的人体应变值。由此建立服装压、服装胸部应变量和弹性模量，代入获得三者间线性方程。同年，Lin等[41]同样利用有限元模拟法尝试预测身着运动衣的男性腿部的服装压。该项研究不仅构建出详细的腿部模型，而且进一步的构建出了具有非线性弹性材料属性的运动服模型。在有限元软件中将运动服模型穿套在腿部模型上，从而模拟出在穿戴该种运动服时的男性腿部的服装压、应变值等。并将模拟值与相同情况下的实际测量值进行比对，证明其具有较高的一致性。

研究者们同时也在不断地完善着经典的主观评价与客观实验相结合的方法。2016年，陈丽华[42]采用“舒适服装压范围→对应的拉伸力范围→对应的拉伸率范围→舒适压力范围内弹性服装的宽裕量”的研究思路，对20种常用不同弹性的弹力针织物及其服装，测量出在定拉伸率下针织物的拉伸力及服装压，并分组构建出相应的线性回归方程。研究表明定伸长力与服装压和拉伸率均为显著的线性相关关系。2017年，胡立娟[22]使用薄膜压力测试系统测试了氨纶弹力网眼织物的服装压，得到服装压与织物的定伸长力、初始模量和拉伸回复率之间的关系；而后以舒适服装压作为标准参照，确定舒适织物的结构参数和拉伸弹性。表明内衣压力与织物的初始模量、定伸长力呈正相关性，而与拉伸回复率的相关性不显著。显然，由舒适服装压得到对应的织物性能参数是可行的。2017年，Liu等[43]采用主观舒适性评价与客观拉伸实验相结合的方法，首先测量样品围带等部位长度，获得定伸长率下的拉伸张力，计算出等效服装压；结合结构参数和张力数据，建立预测围带服装压的方程；根据主观评价确定文胸的舒适服装压的范围。

典型压力服装的服装压与伸长率的相关性见表3。

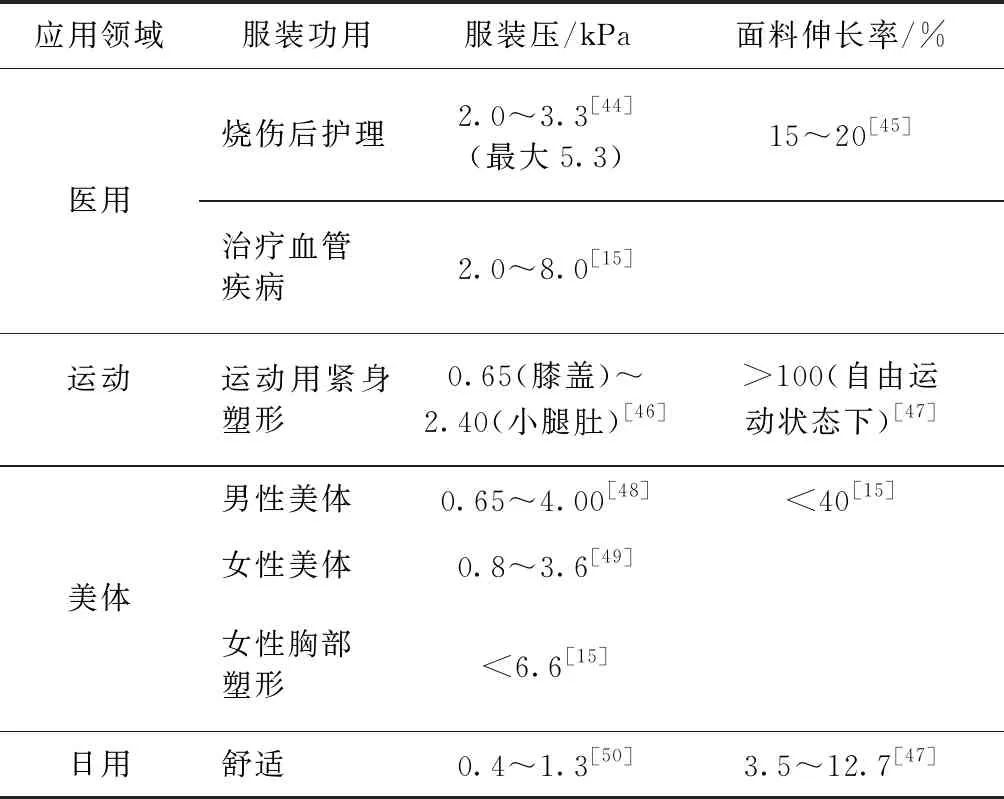
表3 典型压力服装的服装压与伸长率的相关性

3 现有研究存在的问题

现有研究明确了舒适服装压与人体曲率半径和织物力学性能有着明确的相关性，并且可以由舒适服装压反推得到对应织物的性能要求。但是现有的研究仍然存在如下不足：

①无论是理论计算还是有限元法，对于人体模型的处理通常是将其简化为表面光滑平整没有起伏、或具有一定起伏的圆柱体，并且对人物模型赋予其均一的属性。如果需要更加精确的模拟和计算，则应该探索建立更加贴近人体表面形状并具有多种属性的复杂模型。

②典型测量服装压的方法是在服装内衬入电子压力传感器，以此记录该位置点的压力动态变化情况。但是服装舒适性的感受通常是服装面与人体表面相接触感知的。由压力传感器测得的多个点的局部压力与“服装-人体”接触面的服装压舒适度评价，“点-面”之间的相关性仍有不足。

③利用有限元模型模拟服装压的方法尚不成熟。常将服装模型简化为具有一定属性的“壳结构”，或者直接在软件中对人体模型施加已知的载荷。以上的方法均不能有效表现出真实服装穿着过程中，纺织品带来的复杂力学情况。

④现有研究中，对于服装压舒适性的判断方法多采用人体试穿后，试穿者口述此时舒服或者不舒服然后记录此时的服装压是否为舒适服装压。这样的测试结果受试穿者心情、生理状态、环境影响较大，测试结果不稳定，可靠程度较低。目前已有研究者尝试让电脑对服装压数据进行学习，最终实现通过电脑评估虚拟服装穿着的合身性[51]。但是总的来说，目前尚没有一套具有严格限制条件的、完善的舒适服装压判定方法出现。

⑤现有对服装压的研究多局限于泳衣、压力臂套等紧身纺织品，而制服类服装加放量小、塑形性强，活动过程中比休闲类衣服更加容易感受到服装压，目前尚缺少对合体制服类服装压的研究。

⑥目前对于服装压的研究多集中在“瞬时”服装压，即织物或服装在某一刻测出的服装压是多少，然后将其与织物力学性能相联系。较少有人研究服装压在时间、使用次数等条件作用下发生的变化，即服装压的“抗疲劳性”，并将某一过程下变化的服装压与织物力学性能相联系进行分析。

⑦服装压由面压、质量压和集束压3部分组成，现有研究均没有加以区分，统一在服装压下进行研究，但是三者在不同类型服装中的重要程度有显著区别。例如制服类服装以质量压为主，相对应的，纱线线密度等就对服装压的影响甚大；而在泳衣中，集束压占据了主导地位，那么研究织物的弹性模量等力学性能就具有更重要的意义。目前尚没有研究者对此进行归纳整理，并在此基础上进行服装压与织物力学性能相关性的研究。

4 结束语

已有的研究明确了舒适服装压与织物模量、形变量、形变时的应力及人体曲率半径相关，其中与织物相关的3个参数，也正是弹性织物最重要的弹性评价参数。例如大变形量的运动/紧身类服装，需要模量小、易伸长、易回复的弹性织物；小变形量的制服/西服类服装，为了满足适体性的要求，需要模量相对较大、不易伸长、伸长后回复性好的弹性织物。不同服用场景、不同的织物对织物力学性能提出了不同的细致要求。为了开发出穿着理想舒适的服装，需要研究各类服装在使用过程中的舒适服装压及其与织物力学性能的相关性，构建舒适服装压与织物力学性能间的定量关系，进而指导织物的研发。