消极式凸轮开口回综涡簧动态设计与仿真

邱海飞，李春风，党 波，黄鹏飞

(1.西京学院 机械工程学院，陕西 西安 710123； 2.承德石油高等专科学校 工业中心，河北 承德 067000)

消极式凸轮开口被广泛应用于高速宽幅织机，在凸轮轴回转过程中，开口运动需要借助弹簧弹力来实现综框回综[1]。回综弹簧结构型式主要有2种，即直吊式拉压弹簧和涡旋式平卷片簧。在梭口形成过程中，当片综纱线根数较少时，回综弹簧的初张力和初变形也相对较小，2种弹簧均可采用；当片综经密增大时，作用于综框的纱线张力也会随之增大，考虑到开口构件的承载能力，要求回综弹簧刚度不宜过大，因此必须使其产生较大初变形，此时若再采用直吊式回综弹簧，将使提综运动过程中的弹簧伸长量相当之大，难以合理安排综框升降运动的吊综空间[2]。这种情况下，采用平卷涡簧能够有效增大初变形与开口高之比，从而有效解决回综弹簧与机体结构之间的矛盾。

实际工况下，消极式凸轮开口的回综弹簧多以直吊式为主。尽管如此，涡簧回综在某些特定织造工艺条件下亦具有重要应用价值，尤其是在织造宽幅重型织物时，涡簧回综的空间优势和积极作用更是显而易见。本文结合涡簧结构和回综工艺要求，通过理论计算、程序编译和多平台协同设计，实现了一种回综用平卷片簧的动态设计与性能仿真。

1 阿基米德螺旋线

平面涡卷弹簧是由等截面细长材料按照平面螺旋线型绕制而成，其扭矩能量与弹簧卷绕圈数及变形角密切相关。根据相邻圈曲线是否接触，可将平面涡卷弹簧分为接触型和非接触型2类，其中，非接触型平面涡簧常用于产生反作用扭矩，可满足消极式凸轮开口回综弹簧工艺要求。

以阿基米德螺旋线为依据，构建用于绕制非接触型平面回综涡簧的螺旋线型。阿基米德螺旋线亦称等速螺线，其极坐标方程如式(1)所示，在此，令a=35、b=3.5，通过MatLab编程计算和数据可视化，构建如图1所示极坐标下的阿基米德螺旋线，由曲线形态可知，该螺旋线绕中心点共旋绕5圈，旋角范围为0～10π。

r=a+bθ

(1)

式中：r为螺旋线极径，m；θ为螺旋线极角，rad；a、b分别为控制螺旋线的旋转角度和相邻螺旋线间距的实数[3]。

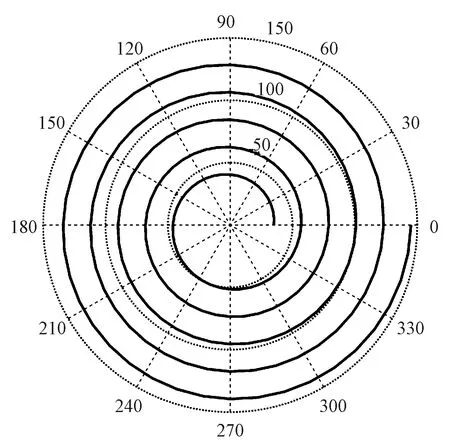
图1 阿基米德螺旋线

2 涡簧设计计算

根据我国机械行业标准JB/T 7366—1994《平面涡卷弹簧设计计算》的规定，对于非接触型平面涡卷弹簧的设计计算，应在已知变形角φ的基础上计算其性能参数。当弹簧圈数n小于3时，由于存在较大误差，应进行试验修正。由已构建的阿基米德螺旋线可知，回综涡簧圈数为5，其变形角φ和刚度T′的计算方法如式(2)(3)所示[4]。

(2)

(3)

式中：φ为涡簧变形角度，rad；T′为涡簧刚度，(N·m)/rad；K1为系数，外端固定时为1，外端回转时为1.25；T为涡簧扭矩，N·m；l为涡簧工作长度，m；E为涡簧材料弹性模量，GPa；b为截面宽度，m；h为截面厚度，m。

JB/T 7366—1994中的平面涡卷弹簧适用于矩形截面材料，其宽度b=5～80 mm，厚度h=0.5～4.0 mm。由文献[2]可知，织造中型棉织物时，回综涡簧变形角φ初始值为4.84 rad，最大值为5.7 rad。根据平面涡簧标准设计规范，选取设计参数b=10 mm、h=2.2 mm；涡簧材料选用弹簧钢50CrVA，其弹性模量E=197 GPa；凸轮提综运动过程中，回综涡簧为外端回转，故选K1=1.25；阿基米德螺旋线工作圈展开长度l=2.83 m。由式(2)可变换得出平面涡簧扭矩计算方法，如式(4)所示，将各设计参数代入式(4)，计算得出回综涡簧初始扭矩为2.39 N·m，最大扭矩为2.82 N·m。将扭矩T和对应变形角φ代入式(3)，计算得出回综涡簧刚度T′≈0.49 (N·m)/rad。

(4)

3 涡簧承载性能分析

3.1 有限元建模

提取MatLab中的阿基米德螺旋线二维坐标向量，通过数据处理将其扩展为三维笛卡尔坐标(X,Y,Z)向量[5]，如图2所示，在此基础上生成基于SolidWorks平台的三维空间螺旋曲线，并由螺旋扫描特征建立涡簧三维CAD实体模型，同时在涡簧起始端和终止端构建用于固定连接的内勾与外勾特征。

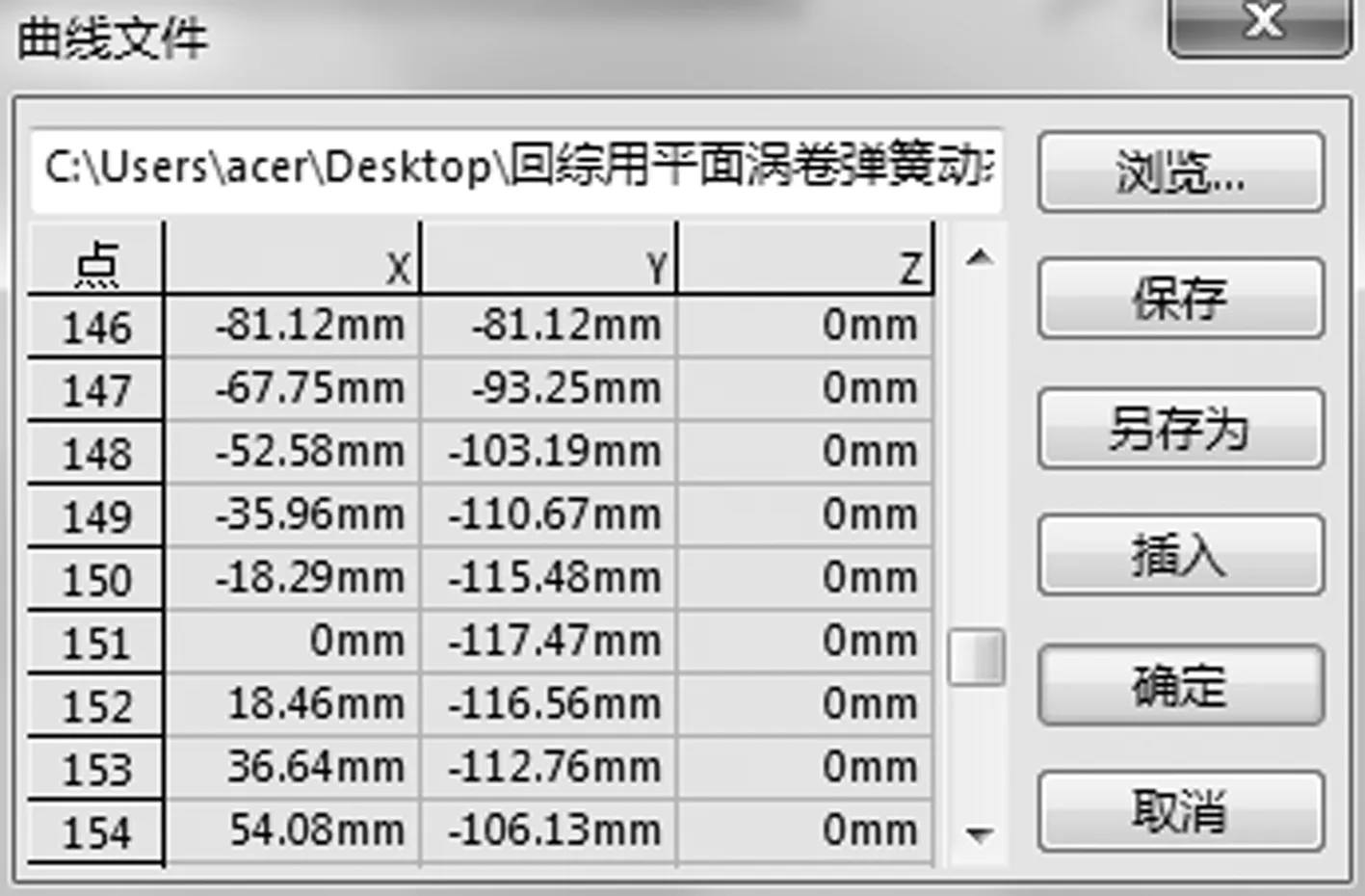
图2 螺旋曲线数据处理

通过数据接口程序将回综涡簧CAD模型导入ANSYS，利用SOLID185单元对涡簧进行网格划分，建立如图3所示有限元模型。根据回综涡簧设计计算结果，将已知扭矩T转化为涡簧外端连接综框位置处的集中力，如图3涡簧外勾处沿Y轴正向的集中载荷F所示。由于回综涡簧工作时内端固定、外端回转[6]，因此在涡簧内勾位置施加固定约束。

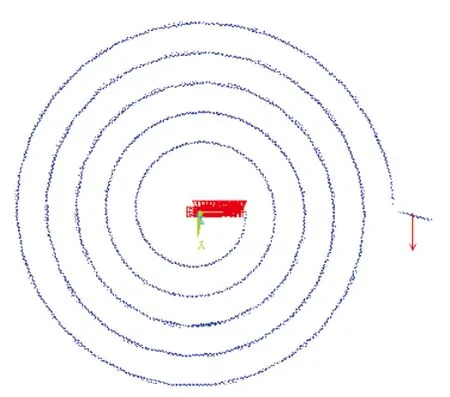
图3 涡簧有限元模型

3.2 形变与应力

为深入研究回综涡簧在卷绕过程中的形变和应力分布，对其进行有限元静力学分析。由图4所示形变状态可以清楚看到，相对于回综涡簧初始形态(图中虚线)，当变形角φ达到最大值5.7 rad时，涡簧外端在集中载荷F作用下沿Y轴正向发生明显位移，此时综框运动至下限位置，使涡簧各圈绕回转中心被卷紧拉伸，并由此产生反向作用扭矩。可见，涡簧的形变特征符合消极式凸轮开口回综工艺要求。

图4 涡簧形变云图

分析图5涡簧应力云图可知，随着回综涡簧被卷紧，应力分布由外圈向内圈逐渐增大，当变形角φ达到最大时，涡簧内端位置最大应力为1.9×108Pa。消极式凸轮开口属于典型高速运动机构，综框升降过程中回综涡簧长期处于反复卷绕拉伸状态，根据JB/T 7366—1994可知，当涡簧反向扭矩作用次数大于105时，其材料许用应力可按式(5)确定，其中σb=1.45×109Pa，在此取[σ]=0.55σb=7.98×108Pa。由此可知，当回综涡簧被卷紧时，最大应力远小于许用应力，满足强度条件设计要求。

[σ]=(0.5～0.6)σb

(5)

式中：[σ]为材料许用应力，Pa；σb为抗拉强度，Pa。

图5 涡簧应力云图

3.3 振动特性

在约束状态下对回综涡簧进行模态分析，提取低阶(1～6阶)自振频率及振型，如图6所示，分析可知，涡簧前6阶自振频率均小于1 Hz。实际工况下，由于凸轮提综和涡簧回综的运行速度很高，使得凸轮轴转速频率和综框升降速度频率远远高于1 Hz，因此消极式凸轮开口不会对回综涡簧振动特性产生不利影响。

图6 涡簧1～6阶自振频率及振型

比较1～6阶振型可知，回综涡簧的1、3、4阶振型相似，均表现为XOY平面内的旋转振动变形，而2、5、6阶振型在出现旋转振动的同时，还发生了不同程度的扭转振动。通过模态振型分析，可有效预测涡簧在各阶自振频率下的振动模式，为其动力学特性评估提供重要依据。

4 涡簧动力学仿真

4.1 柔性化模型

在ADAMS/View环境下创建动力学仿真模型，根据消极式凸轮开口结构原理对回综涡簧施加运动约束，并利用AutoFlex模块对涡簧仿真模型进行柔性化处理。在螺旋线中心端施加一个恒定角速度模拟涡簧转角变形，运行柔性体动力学仿真，如图7所示，为柔性涡簧在卷紧过程中某一瞬时的变化形态，可以清晰地看到，当凸轮提综时，涡簧各圈依次发生卷绕变形，且变形过程中各圈的应力分布明显不同。

图7 涡簧柔性变形

4.2 涡簧特性曲线

回综涡簧转角φ的变化曲线如图8所示，分析可知，随着时间t变化，涡簧逐渐被卷紧，这一过程中转角φ与时间t成正比增长关系，符合非接触型平面涡卷弹簧的结构特性。

涡簧刚度曲线理论上应为一条直线，即刚度曲线的斜率为恒定值，但实际上在涡簧卷紧初期，由于外圈存在空转，其刚度曲线呈线性或近似线性变化[7]，如图9所示，当凸轮提综或涡簧回综使转角φ增大到一定程度时，涡簧各圈均发生卷紧变形，此时刚度曲线斜率在逐渐增加，说明涡簧刚度在随着变形圈数的增加而增大，即刚度曲线变为渐增型，回综涡簧扭矩快速增大，与理论刚度曲线基本一致。

图9 回综涡簧刚度曲线

4.3 涡簧储能密度

由式(6)所示平面涡卷弹簧储能公式可知，回综涡簧在卷紧过程中产生的弹性势能U等于扭矩T与转角φ乘积的一半[8]。根据回综涡簧柔性体动力学仿真结果，在MatLab中编程计算涡簧储能曲线，如图10所示。

图10 回综涡簧储能曲线

十分明显，涡簧从卷绕开始就存储能量，随着涡簧卷紧和转角增加，涡簧存储的能量也相应增大；当转角增大到一定程度时(约0.376 rad)，涡簧储能曲线增幅明显加快，类似于刚度曲线的渐增型变化；当涡簧完全卷紧时(0.870 rad)，其存储的能量U=3.28 N·m·rad。

(6)

将U值代入式(7)，计算得到回综涡簧储能密度ρE=6.75 (N·m·rad)/kg，即涡簧卷紧时单位质量内所存储的能量。储能密度越大，涡簧能够产生的反作用扭矩也就越大，对于掌握和评估涡簧回综承载能力具有重要参考价值。

(7)

式中：U为弹性势能，N·m·rad；T为涡簧扭矩，N·m；φ为涡簧变形角度，rad；ρE为涡簧储能密度， (N·m·rad)/kg；l为涡簧工作长度，m；ρ为涡簧钢材料密度，kg/m3；s为涡簧横截面积，m2。

5 结束语

涡簧回综避免了吊轱辘回综由于皮带伸长所造成的开口不清，不仅便于安排结构空间，而且能够使综框运动更为平稳。通过基于阿基米德螺旋线的回综涡簧设计计算和有限元分析，确定了涡簧的结构特征、应力变形和模态参数，有助于准确理解和掌握回综用平面涡簧的静动态特性；通过柔性体动力学仿真，计算获得了回综涡簧刚度曲线及其储能密度，明确了涡簧卷紧过程中的动态变形和储能特性，为回综涡簧的动力学仿真和可靠性设计提供了重要技术参考。以此为基础，后续研究可考虑将回综涡簧与消极式凸轮开口装配连接，并通过机构动力学仿真进一步评估涡簧的回综性能，为新型涡簧回综装置的设计开发提供了有力支持。