基于声学模态分析的燃气锅炉热声振荡研究

鲁朋朋,潘 登,朱 彤,齐国利,王中伟

(1.同济大学 机械与能源工程学院，上海 201804;2.中国特种设备检测研究院，北京 100029)

近年来国家及各地政府相继出台政策要求工业锅炉必须实现超低氮排放，2015年北京市颁布的锅炉大气污染物排放标准规定[1]：2017年3月31日前的新建锅炉氮氧化物浓度排放限值为80 mg/m3，2017年4月1日后的新建锅炉氮氧化物浓度排放限值为30 mg/m3；2018年上海市颁布地方标准[2]，要求2020年10月1日后，燃气锅炉NOx排放浓度在50 mg/m3(标准)以下。目前燃气锅炉采用的低氮技术主要包括烟气再循环、贫燃预混燃烧、燃料分级和空气分级等[3-7]，但在这些低氮燃烧技术的应用过程中经常出现燃烧不稳定现象[8-9]，表现为炉膛空间大振幅的低频压力脉动(<50 Hz)[10-11]，不仅燃烧噪音大，而且锅炉振动可能导致结构损坏，严重影响锅炉运行安全。因此，燃气锅炉领域的热声振荡研究对于低氮燃烧技术的应用和锅炉安全运行具有重要意义。

热声振荡是燃烧的周期性热释放与燃烧室的本征声学模态耦合而产生的不稳定燃烧现象[12]，涉及声学、流体力学、化学反应动力学、传热和传质学等众多学科，而且涉及的流动和化学反应的空间与时间尺度跨度大。国内近几年关于燃烧热声不稳定的研究逐渐增多，张昊等人[13]对天然气预混燃烧过程中热声耦合振荡现象进行了实验研究，分析不同当量比、热负荷和进出口边界条件下的燃烧动态过程，结果显示振荡频率分布在500 Hz附近并随着当量比的减小有所增加。孙培锋等人[14]采用ANSYS分析了燃用航空煤油的贫预混预蒸发模型燃烧室的前4阶轴向声学模态频率，发现实验中所激励出的振荡燃烧主频144 Hz和第二阶轴向声学模态频率吻合的很好。付虓等人[15]针对模型预混燃烧室的燃烧不稳定性现象进行了实验研究和数值模拟，得到周期性旋涡脱落频率260 Hz以及系统声学模态频率，其中第三阶声学模态频率与实验值基本一致，说明维持不稳定性的机理为周期性涡脱落和燃烧室的第三阶声学模态形成了耦合。王昆[16]运用Comsol模态分析模块求解预混模型燃烧室的模态频率和振型，对预混模型燃烧室进行了声学模态分析，结果表明声学模态分析可以预测热声振荡频率，认为声学模态分析是研究热声振荡问题的强有力工具。虽然热声振荡研究已经取得了较为丰富的研究成果，但大多数研究主要集中在预混燃烧或燃气轮机等领域，燃气锅炉领域热声振荡研究相对较少，尤其是燃气锅炉采用低氮燃烧技术后出现的低频燃烧振荡。

本文选取350 kW扩散燃烧燃气锅炉为研究对象，通过实验获取了不同过量空气系数条件下锅炉燃烧系统的压力波动特征，并采用声学软件Actran求解Helmhotlz方程，耦合CFD模拟结果，对锅炉燃烧系统在实验工况下的声学模态进行分析，研究了不同过量空气系数下燃气锅炉系统的空腔声学固有模态特征。

1 实验设备及研究方法

1.1 实验装置及测量方法

实验台主要设备包括：空气供给设备、天然气供给设备、锅炉本体、燃烧器、换热器和冷却水循环设备及相关的连接管道，实验台系统示意图如图1所示。锅炉本体额定负荷为350 kW的卧式燃气锅炉，炉膛为圆柱形单程直筒结构，直径0.4 m，长2 m，锅炉结构如图2所示。燃烧器采用一体式扩散燃烧器，通过变频器调节风机风量，图3为燃烧器实物图和头部结构的示意图。实验中通过控制锅炉冷却水流量，保证锅炉内水温稳定在90 ℃左右。炉膛后部连接气-气板式换热器，可以通过控制阀门调节冷却空气风量，进而控制排烟温度。

图1 实验台系统图

图2 卧式燃气实验锅炉系统图

图3 燃烧器实物图和头部结构示意图

采用动态压力传感器测量炉膛的压力波动，采用NI9203高速数据采集卡结合LABVIEW数据采集与存储程序，进行动态压力数据的采集与保存，数据采样频率为1 000 Hz。采用涡轮流量计计量燃气流量，采用Testo 350 对尾部烟气的氧含量进行测试，并根据燃气组分和尾部烟气氧含量换算过量空气系数。

实验中保持燃气流量恒定，通过调整风机频率，实现不同过量空气系数工况。实验中天然气流量为29 m3/h(标准)，过量空气系数α的控制范围为1.19～1.59。

1.2 声学模态分析

锅炉炉膛及其连通空间的声学模态与炉膛的几何结构、介质的物性和声学边界有关，将燃气锅炉系统看作一个封闭式声腔，在给定的激励频率范围条件下，通过求解Helmholtz方程，可以得到锅炉炉膛及其连通空间的声学模态。对于锅炉炉膛及其连通空间，由于燃烧和换热等过程导致炉膛、烟管及换热器内温度、密度等分布不均匀，因此在对炉膛及其连通空间进行声学模拟时，需要考虑空间介质的物性分布。在考虑介质物性分布不均条件下，无源的Helmholtz波动方程[17]见式(1)。波动方程中涉及到的介质物性包括密度和声速。

(1)

式中：ρ(x,y,z)为密度分布；p(x,y,z)为声压分布；c(x,y,z)为声速分布；ω为角频率。

本文使用ACTRAN软件的直接频响分析模块，求解声源激励条件下的Helmholtz方程，即锅炉及其连通空间在一定带宽的声源激励条件下的频率响应，基于有限元方法考虑一个具有固壁边界腔体的系统方程见式(2)[18]。

(K+iωC-ω2M)X(ω)=F(ω)

(2)

式中：K，C，M分别为系统的刚度、阻尼与质量矩阵；向量F(ω)代表激励源输入，向量X(ω)代表各有限元节点的声压输出。如上齐次方程具有一组非零解，并对应一组特征值ω=ωi。每个特征值对应一种特定的声压分布φi，称为特征模态，特征值对应的特征频率为fi=ωi/2π。

通过以上方法求解有源条件下的Helmhotz方程，得到炉膛及其连通空间的声学模态。为了得到炉膛及其连通空间的介质物性(密度和声速)分布，首先采用ANSYS FLUENT 计算获得了炉膛及其整体连通空间的温度、密度和声速分布。将计算域中的温度场、密度和声速等分布通过ACTRAN中ICFD模块插值到声学网格中。结合ANSYS FLUENT和ACTRAN模拟炉膛及其连通空间的声学模态的计算流程如图4所示。

图4 声学软件耦合CFD结果进行直接频响分析流程图

锅炉系统连通空间的几何结构如图5所示，包含入口段、扩散燃烧器、炉膛、连接管道、换热器、排烟管。在针对入口段到连接管道的CFD计算中，湍流采用RNGk-ε模型，燃烧化学反应采用组分输运模型中的Eddy Dissipation模型，辐射采用DO模型；空气入口和燃气入口采用速度入口边界条件，排烟出口采用压力出口边界条件，压力为大气压；炉膛壁面采用100 ℃定壁温边界，与实验边界条件一致，换热器以及排烟管道部分给予第三类边界条件。

图5 封闭式声腔计算区域及声学条件设置

对于系统空间声学模拟，所有壁面边界定义为刚性壁面，出口与大气相连，边界条件定义为压力为0，入口占整体模型比例较小且根据燃烧器阻塞比较大，声学边界条件设置为全反射边界。燃烧热释放脉动是炉膛空间声学波动的主要源头，根据CFD模拟结果，燃气喷嘴下游0.3 m处热释放最大，因此在燃气喷嘴下游0.3 m处设置点声源压力脉动激励，激励声源频率范围为0～100 Hz，间隔为0.1 Hz，并于压力测量点处设置声源响应监测点。

2 结果及分析

2.1 炉膛压力振荡分析

在天然气流量为29 m3/h(标准)时，实验测试了不同过量空气系数条件下炉膛内的压力波动，采用快速傅里叶变换(FFT)方法对炉膛的压力波动数据进行分析，每个工况压力波动数据处理时间段为10 s，FFT分析结果如图6所示。压力波动幅值频率主要集中在低频范围(<120 Hz)，其中压力幅值的峰值频率分布在20～30 Hz。压力波动幅值第一峰值频率随着过量空气系数的增加而降低，过量空气系数α由1.19增加至1.59时，压力波动幅值第一峰值频率由25.6 Hz降低至24.3 Hz。热声耦合的燃烧不稳定是火焰的热释放与系统空间声学模态相互作用的结果[14]，燃烧不稳定的压力振荡频率与锅炉系统的声学模态有关，为了分析燃烧不稳定产生的特征频率与空间声学模态的关系，本文模拟了实验工况条件下燃气锅炉系统空腔的固有声学频率。

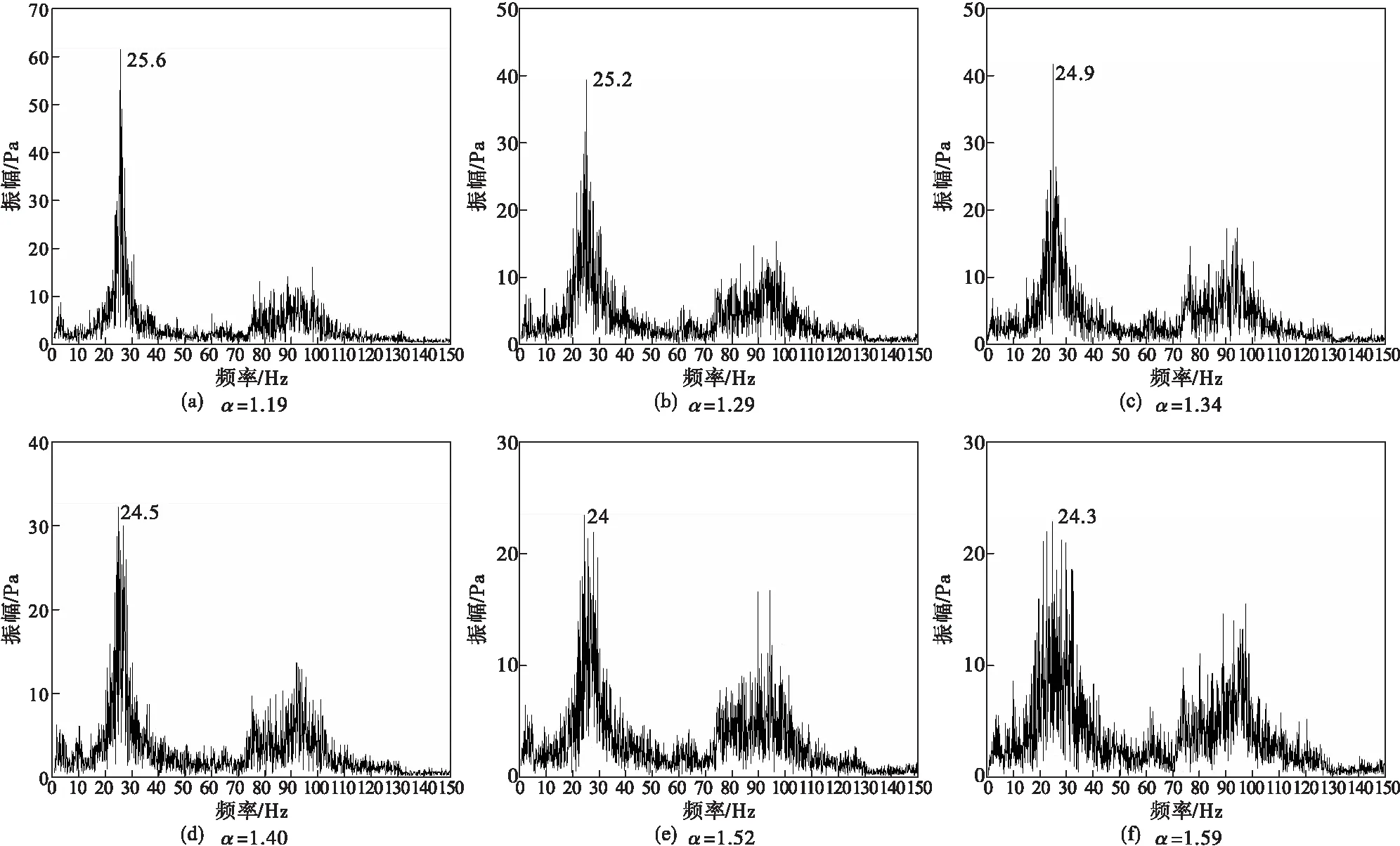
图6 燃气流量29 m3/h(标准)不同过量空气系数α下炉膛压力振荡数据的频谱分析

2.2 声学模态分析结果

通过CFD方法模拟了炉膛及其连通空间整体在不同过量空气系数条件下的温度分布，不同过量空气系数条件下炉膛空间纵截面的温度分布如图7所示。随着过量空气系数增大，火焰长度变短且整体温度降低，温度分布差异明显。

图7 不同过量空气系数α下炉膛空间的纵截面的温度云图

根据理想气体声速计算公式[17](见式(3))，因此同种气体当地声速主要取决于温度。不同过量空气系数条件下炉膛及其连通空间的当地温度分布有明显差异，炉膛出口位置的当地声速最高相差400 K。对于密度分布，锅炉炉膛空间为常压，不同工况条件下炉膛及连通空间的压力一致，因此空间的密度分布也主要受温度分布影响。

(3)

式中：γ为绝热指数；R为气体常数；T为介质温度,K。

将燃烧数值模拟定常计算得到的声速、密度分布插值到声学网格、不同过量空气系数α下炉膛空间的纵截面的声速云图中，见图8。

图8 燃烧数值模拟计算结果插值声学网格后声速密度分布

对图5中的炉膛以及炉膛出口烟管空腔进行直接频响分析，得到不同过量空气系数下的频响曲线见图9，频响曲线对应的峰值为声学固有模态。随过量空气系数的增加，炉膛一阶纵向模态频率从85.5 Hz变化到49.5 Hz，由于炉膛内的平均温度变小，因此相同阶数模态的频率也减少。

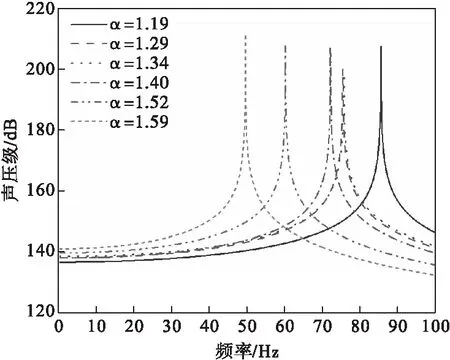
图9 炉膛以及炉膛出口烟管在不同过量空气系数下的频响曲线

对图5中结构整体进行直接频响分析，得到过量空气系数从1.19变化到1.59的六个工况下在100 Hz以内的频响曲线，见图10。不同过量空气系数下，一阶、二阶的声学模态纵波占主导对应的声学模态频率分布集中，其中二阶声学模态频率分布在25 Hz附近，后四阶由于纵波与横波的叠加模态较复杂。

图10 不同过量空气系数的直接频响曲线

以过量空气系数为1.34为例，其二阶声学模态频率为25.4 Hz，在100 Hz以内前六阶声学模态频率声压级云图如图11所示，前二阶声学模态为纵波主导，主频低于研究对象的截止频率，声波以平面波形式传播，后四阶声学模态为横波和纵波叠加较复杂。在模态振型分析中一阶声学模态压力波腹(声压级峰值)出现在换热器位置，二阶声学模态压力波腹出现在换热器位置。

图11 过量空气系数为1.34时前六阶声学模态频率声压级云图

通过以上分析，一方面通过对比有无换热器部件的频响曲线，一阶声学模态频率分布区间从45.5～85.5 Hz变化到1.6～7.3 Hz，在燃烧炉膛出口后的换热器等附件由于温度梯度较大有必要在声学模态分析中予以考虑。另一方面随过量空气系数改变，燃气锅炉系统前二阶声学模态频率分布较集中，不同声学模态频率声压峰值位置不同，其中二阶声学模态频率分布区间为24.2～27.5 Hz，声压峰值在换热器部位，与实验结果进行对比可以看出压力振荡主频与系统的二阶声学模态频率分布区间一致。

3 结 论

针对燃气锅炉的燃烧压力振荡现象进行了实验研究和数值模拟，利用动态压力传感器采集炉膛压力脉动数据，并通过声学软件耦合不同燃烧工况下的CFD定常模拟结果，得出如下结论：

(1)实验中燃烧室在不同过量空气系数都出现了低频压力振荡现象，压力振荡主频分布区间为24.3～25.6 Hz。

(2)对燃气工业锅炉系统，炉膛尾部的换热器和排烟管道空间对锅炉整体声学模态影响较大，在声学模态分析中必须予以考虑。

(3)本文采用声学软件耦合CFD燃烧数值模拟的方法，计算得锅炉系统空腔整体的声学二阶模态频率与实验测试得到相同工况下的压力波动峰值频率一致，说明考虑温度场分布和边界声学特征的声学模态分析可以反映锅炉压力振荡主频，可用于预测燃气锅炉系统热声振荡频率。