数形结合,构建小学数学解题模型
曾令发

【摘要】“模型就是通过对问题现象的分解,利用我们考虑得来的原理吸收一切主要的因素,略去一切不主要的因素,所创造出来的一副图画……”数学图形模型是指利用图形对变量间的关系作分析基础,构建图形将问题直观地表达出来,或将实际问题直接与几何知识、代数知识结合,求解问题。抽象逻辑思维的培养依托于几何图形,同时,也为学生提供具体、形象、直观的解决问题的方法,把最适当的认识方式变为学生所能掌握的形式,不仅提高学生的学习效率,而且培养了浓厚的学习兴趣。
【关键词】模型;数形结合;数学图形
数学是关于模式的科学而不仅仅是关于数的科学。学生的学习过程是一种以主体已有知识的经验为基础的主动建构活动。数学模型是关于部分现实世界和为一种特定目的而作的一个抽象的、简化的数学结构,它能提供处理对象的最优决策。例如,历史上著名的“哥尼斯堡七桥问题”的答案就是一个典型的数学模型。在此,笔者首先给学生讲“植树问题”的过程。
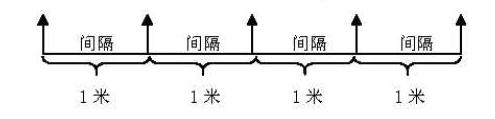
题目:同学们张开手,5个手指人人有,手指之间几个空,请你仔细瞅一瞅。
笔者举起手来,张开五指,学生们模仿着笔者的动作,大声回答说:“四个空。”笔者告诉他们,“空”是俗话,数学上把“空”叫做“间隔”。然后,笔者接着问:“5个手指之间有几个间隔?”学生们齐声答道:“4个间隔。”此举叫做“配个原形”。“手”就是“手指”和“空”所代表的一类事物的数量关系的原形:5-1=4,即“手指数-1=间隔数”。
笔者把这个式子板书出来,接着就又出了下面的题:
题目:(种树)小朋友在一段路旁种了5棵树,这5棵树之间有几个间隔?若每个间隔长1米,这段路有多长?
学生们一下就看出来了:5棵树之间有4个间隔,4个间隔共长4米。
笔者紧接着就引导学生写出下式:5-1=4,即棵数-1=间隔数(两头都种树)。
这实质上就是建构了空间一维直线上的点数和它们的间隔数之间的数量关系。可以看出,这个关系和手的情形是同样的。这种共同数量关系及其表达式就可以作为一种数学模型看待。
然后,笔者继续引导学生扩展考察的范围:题目(钟打点)——小明家的钟会打点报时,5点钟打5下,4秒钟打完。按这样,你知道10点钟打10下需要几秒钟打完吗?
笔者仍然引导学生先画图,打一下,画一个点,这就使学生在不知不觉中把时间观念用图形(线段和点)转化为空间形式来表达了。
由图可见,5个点之间4个间隔,4个间隔是4秒,显然每个(时间)间隔是1秒。“5-1=4”也符合:点数-1=间隔数。进而得出:10-1=9(个间隔),从而得出打10下需要9秒钟打完。此时,笔者借机告诉学生,与前面题目中的“空间间隔”不同,这道题中的间隔叫“时间间隔”。此外,还可以继续扩展这一模型应用到其它的问题上。
题目:1.(锯木头)把一根木头锯成5段要付锯工费用1元。如果把同样的另一根木头锯成13段,应付锯工费多少元?2.(上楼梯)小明家住五楼。他数了数两个楼层之间的楼梯共有10个台阶。他想知道自己从一楼上到五楼要上多少个台阶,你能帮他算出来吗?
把这两题解答完后,师生一起回顾以上各题,找出它们的共同点,即抽象出这类事物中共同的数量关系,仍以“植树问题”为代表,写成:棵数-1=间隔数(两头都有树)。
按照习惯,我们就把这一类问题叫做“植树问题”。通过以上学习,随着年级的升高,学生就可以运用这一模型进一步解决那些更为复杂的问题。如,57辆军车排成一列通过一座桥,前后两辆车之间都保持2米的距离。桥长200米,每辆军车长5米。从第一辆车头到最末一辆车尾共长多少米?
整个教学过程就是设法使学生建构起现代模式论的数学观,这也符合布鲁纳说的“从本质上说,一开始不是学习一种技能,而是学习一个一般观念,然后这个一般观念可以作认识后继问题的基础,这些后继问题是开始所掌握的观念的特例。这种类型的迁移应该是教育过程的核心——用基本的和一般的观念来不断扩大和加深知识”。
出于同样的考虑,当学生学了长方形的面积后,我们就可以把长(下转第23版)(上接第22版)方形作为数学模型来对待,就是对某些数学问题的数量关系,用长方形表示出其几何意义或以某种方式可以与几何图形建立联系,将题目中的条件及数量关系直接反映在几何图形中,然后在构造中寻求原题的结论。
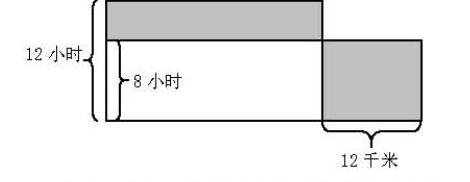
如,一辆汽车从城市开往山区,往返共用20小时,去时的时间是回来的1.5倍,去时的速度比回来的速度慢12千米,汽车往返共行多少千米?
这里用长来表示速度,宽表示时间,构造一个“长方形”,问题就迎刃而解。
触类旁通,只要具有类似计算长方形面积的乘法应用题都可以构造“长方形”模型来求解。在此略举几例,以示佐证。
一是解平均数问题。例如,五(1)班数学期中考试平均分为78分,而男生平均分为75.5分,女生平均分为81分,求男女人数的比。
二是解行程问题。例如,甲乙丙三人,甲每分走50米,乙每分走60米,丙每分走70米。甲乙从东村,丙从西村同时出发。丙遇到乙后2分钟又遇到甲,求东西两村的距离。
根据“速度和×相遇时间=路程”的数量关系,可构建下圖来求解。
三是解测量古井问题。例如,用绳子测量井深,把绳子三折来量,井外余4尺;把绳子4折来量,井外余1尺。求井深和绳子的长。
由于井深就是每折的长度减去余在井外的长度,通过构建下图,假设井深为x米,得:(x+1)×4=(x+4)×3.
四是解盈亏问题。例如,一些人共同分担购买小船的钱,如果其中10人后来决定不参加,余下的人每人要多分担1元。当实际付款时,又有15人退出,最后余下的每人又要多分担2元。求原先是多少人?
这题相对复杂些,但只要抓住所构建图中的“等积”关系列方程,答案就自然有了。
在数学能力竞赛中,许多题目只要注意构造模型,初看无从下手的题目会变得简单、明了。例如,通过构造“极端”模型,从问题的最简单状态或最多的情况入手,探索解题方法。如(1)计算:
(2)某人上楼梯的本事有三种:一步一级、一步两级、一步三级,他要从楼下上到10级台阶的楼上,有多少种不同的方法?这两题都可以从最简单的“极端”去考虑。
另外从数点格求积得到启示,可以构造“网格”模型来解题。如,(1)正六边形ABCDEF的面积为6平方厘米,M、N、P分别是所在边的中点,求三角形MNP的面积。(2)长途公共汽车有甲、乙两个终点站,汽车要用4小时才能驶完全程。从上午6时开始,每隔1小时从甲乙两站同时发出一辆汽车,最后一辆车是在下午4时出发。从甲站出发的汽车司机最多能看到多少辆迎面驶来的从乙站开出的车?最少呢?这两题只要构造下面的“网格”图,题目就显得非常容易了。
从这些鲜活的例证中,我们真正领略到了“数形结合,构建解题模型”的意义和价值,也应证了布鲁纳说的“智力的主要任务就在于为经验的顺序构造易于解释的模型,紧接着的命题就是把最适当的认识变为幼小学童所能掌握的形式……学生一旦熟悉了那个适当形式,便能继续掌握更有效能、更精确的认识和使用知识的形式。”相信通过笔者以上的抛砖引玉,今后的教法在一定程度上实现布鲁纳的期待——“把最适当的认识方式变为幼小学童所能掌握的形式”。
参考文献:
[1]连秀云,刘来福.模型解题法(初中数学)[M].北京大学音像出版社,2010.
[2]史宁中.数学结合与数学模型[M].高等教育出版社,2018.
[3]唐振华,张旭芳.数学结合[M].电子工业出版社,2020.

