基于零部件均衡重要程度的混流装配线排序
刘 畅,原丕业,刘佳楠,张 萌
(青岛理工大学 管理工程学院,山东 青岛 266520)
混流装配线是指在同1条装配线上以流水作业的方式混合连续地完成工艺接近的不同类型、不同数量的产品。合理的产品投放顺序有助于降低成本、提高效率,进而提升企业的竞争力。因此,众多学者针对该问题进行了大量的研究。文献[1-7]分别从不同的角度建立关于混流装配线的排序模型,但并未考虑到生产过程中零部件消耗的均衡化。文献[8-14]虽在建立的混流装配线排序模型中考虑到零部件消耗均衡化的因素,但并未考虑到不同类型零部件的消耗均衡情况对生产装配系统重要程度的差异性。因此,在以零部件消耗均衡化为目标的混流装配线排序过程中考虑零部件均衡化的重要程度是十分必要的。
1 问题描述
混流装配线排序问题是一个短期决策问题,每日甚至每班都需要根据市场需求的变化安排合适的排产计划。由于在混流装配线中生产每种产品所需的零部件类型以及数量各不相同,所以不同的投产排序对各类零部件的消耗都是不同的。若零部件消耗不均衡,则会造成在一段时间内某类零件的需求量激增,而其他零件的需求量较少,为了应对某零件的高峰需求,该零件需要维持在1个较高的安全库存,从而造成不必要的浪费。因此,在混流装配线排序时需要对零部件消耗波动进行均衡。由于传统的零部件消耗均衡是为了达到总体目标的最优,即全部零部件消耗波动函数之和最小化,所以个别类型的零部件消耗波动均衡情况一定没有或者是较小地进行改善。若这类零部件的均衡程度相对生产系统更为重要,则必须采用一定的方法保证这类零部件最大程度地优先进行均衡。
2 数学建模
基于以上描述,为了确保重要零部件最大程度地优先进行均衡,本文根据各类零部件均衡对生产装配系统的重要性,分别赋予各类零部件不同的权重,为了简化运算,在1个最小生产循环内构建基于零部件均衡重要程度的混流装配线排序模型
(1)

(2)
(3)
qms-qm,s-1≤1, ∀s∈I,m∈M,
(4)
qms-qm,s-1≥0, ∀s∈I,m∈M,
(5)
0≤qms≤dm, ∀s∈I,m∈M,
(6)
0≤ωg≤1, ∀g∈p.
(7)
式中:I为1个MPS中需要排序的产品数量;s为排产序列中第s个位置;p为零部件的种类数量;M为产品的种类数量;g为类型g的零部件;m为类型m的产品;dm为类型m的产品数量;ngm为装配产品m所消耗零部件g的数量;qms为前s个位置中产品m的数量;ωg为零部件g均衡化重要程度的权重;xsm为0~1变量,当排产序列中第s个位置的产品是m,则为1,否则为0。
目标函数表示考虑零部件均衡重要程度的零部件消耗均衡情况,其中,括号内第一部分表示零部件的理想消耗量,第二部分表示零部件的实际消耗量;式(2)表示任意1个位置只能安排1个产品;式(3)表示排产序列中安排m产品的数量等于其需求量;式(4)、式(5)表示在任意1个s-1的位置到s位置,产品m的数量只能增加1或保持不变;式(6)表示排序中任意s位置前产品m的数量不能大于1个MPS中产品m的需求量;式(7)表示权重的取值范围。
3 自适应遗传算法的设计
遗传算法是由美国教授Holland在1975年提出的1种效仿达尔文生物进化过程的优化算法,即通过对染色体的评价、选择、交叉以及变异等一系列操作,最终得到最优的目标值。但是,传统的遗传算法中的交叉算子和遗传算子往往采用固定的数值,这种方式的弊端在于若种群中出现占据绝对优势的染色体,极易导致求解的结果陷入局部最优。为了避免出现早熟现象,提高全局搜索最优染色体的能力,文中设计新的自适应遗传算法用于解决混流装配线的排序问题。该算法在遗传算法的基础上通过借鉴文献[15]的自适应机制对交叉和变异算子进行动态地调整,可以使模型在求解过程中有效地避免出现早熟的现象。综合以上的分析,可得到本文设计的自适应遗传算法的流程如图1所示。

图1 自适应遗传算法流程
3.1 编码
针对投产排序问题,由于模型的求解结果只与产品对应编码在染色体上的位置有关,与其大小无关,故本文采用符号编码方式。不同类型的产品用不同的数字表示,如A,B,C,D,E 5种产品分别用1,2,3,4,5进行表示,则染色体11223345解码后可表示为AABBCCDE这样一个序列依次进入装配线。
3.2 初始化种群的产生
为了确保初始解的质量以及多样性,在初始化种群的过程中参考小生境技术先进的思想。首先依据1个MPS中各产品的投产比例,分别确定染色体的长度以及种群的规模,然后任意生成满足种群规模大小条件的若干个种群,挑选出每个种群中适应度值排名前10%的染色体,使其组成1个新的种群,最终形成初始种群。
3.3 选择
为了能够更好地选择和保留优秀的染色体,本文采用精英保留策略和轮盘赌相结合的方法。采用轮盘赌的方法虽然可以使适应度值好的染色体有较大的概率被选中复制到下一代,但是无法保证一定被保留。同理,适应度值较差的染色体无法保证被淘汰。并且由于后续交叉和变异的过程中具有随机性,容易出现遗传退化。因此,为防止出现遗传退化解,确保淘汰最差个体,保留最优染色体,故在轮盘赌的基础上加入精英保留策略。即保存并记录父代种群中的最佳染色体,若子代种群相比父代种群没有出现更优秀的染色体,则用保存的最佳染色体替换子代种群中适应度值最低的染色体,否则,将更新当前保存的最佳染色体。
3.4 自适应交叉算子
交叉概率决定了种群中染色体被选中进行交叉从而产生子代的概率,小的交叉概率能够更好地对种群中出现的优秀个体进行保留,但是容易陷入局部最优。大的交叉概率有利于跳出局部最优从而寻求最优解,但是会损害优秀个体,造成算法退化,为了提高算法对局部最优的突破能力以及全局最优的保存能力,借鉴文献[10]的方法,通过评价当前种群染色体的离散程度对交叉概率进行自适应调整,具体计算如式(8)所示。从选择复制产生的子代种群中按照自适应交叉概率pc选取一定数量的交叉父本,两两父代个体之间进行交叉操作。交叉过程如图2所示:首先从父代1中任取一段基因直接遗传到子代1相应的位置;其次,从父代2中依次剔除所选取片段中含有的基因,并将残留的基因依次遗传到子代1剩余的位置中,从而产生新的子代个体。同理,交换父代的位置可产生子代2。将从原种群中选择的交叉父本分别用新产生的子代个体进行替换,进而形成新的种群。

图2 交叉过程
自适应交叉概率pc的计算公式为
pc=

(8)
式中:pcmax为预设最大交叉概率;pcmin为预设最小交叉概率;fmax为当前种群内个体的最大适应度值;favg为当前种群内各个体的平均适应度值;ξ为fmax-favg的敏感性系数。
3.5 自适应变异算子
变异概率决定了种群中染色体被选中进行变异的概率,对种群多样性的保持有着重要意义。本文通过借鉴文献[10]的方法对变异概率进行自适应调整,具体计算如式(9)所示。变异过程具体如下:首先从种群中按照自适应变异概率抽取一定数量的变异父本,其次如图3所示对变异父本中的染色体随机选取两个需要突变的位置进行交换以完成变异操作。

图3 变异过程
自适应变异概率pm计算公式为
pm=

(9)
式中:pmmax为预设的最大变异概率,pmmin为预设的最小变异概率。
根据式(8)和式(9)可知,fmax与favg的差值越大表示当前种群个体越离散,种群多样性越好,此时需要降低交叉概率pc和变异概率pm,从而加速收敛。fmax与favg的差值越小表示当前种群个体越集中,多样性越差,为防止出现局部收敛等问题,需要增加交叉概率pc和变异概率pm。
4 案例分析
已知某公司混流装配线上A,B,C,D,E 5种产品的日均订单需求量分别为(60,20,40,30,20),根据最小生产循环原理可得到A,B,C,D,E的产品比例为6:2:4:3:2,现阶段公司按照AAAAAABBCCCCDDDEE的顺序在最小生产循环内依次对各类产品进行小批量生产,其中,每种产品消耗零部件的类型和数量如表1所示。
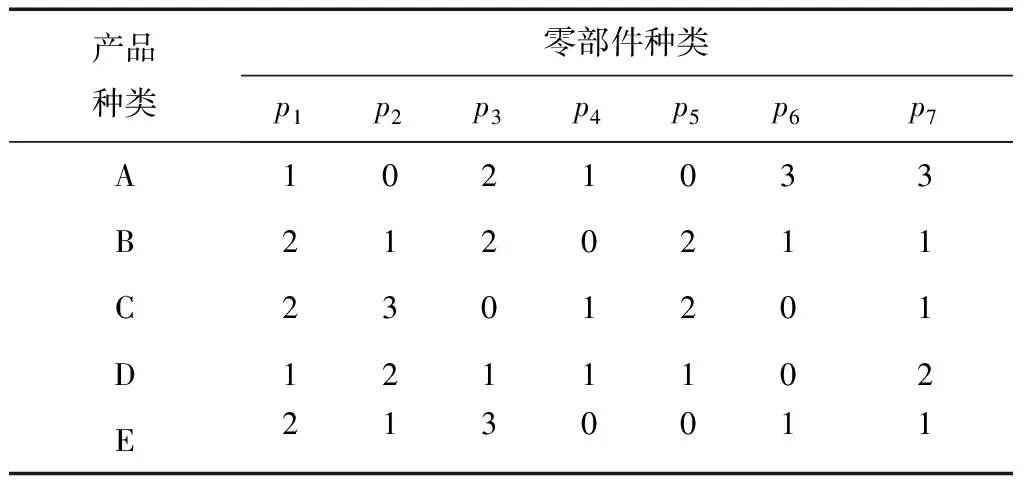
表1 产品-零部件消耗矩阵
本文的算法通过MATLAB R2016a进行编程,计算机处理器参数为Intel(R)Core(TM)i5-8250U CPU@1.6 GHz 1.80 GHz双核处理器,RAM为8 GB,64位Windows10操作系统。经过算法灵敏度计算实验,确定涉及的参数设置如下:种群大小为30,最大交叉概率与最小交叉概率分别为0.9和0.5,最大变异概率与最小变异概率分别为0.1和0.01,迭代代数为100,ξ为10,根据各零部件均衡化重要程度确定权重ωg=[0.4,0.4,0.4,0.4,1,1,0.4]。
4.1 算法对比
利用自适应遗传算法进行求解,得到最终的混流装配线排序方案为DABCAECADACACEBAD,目标函数值为31.282 4。其中,自适应遗传算法收敛曲线如图4所示。

图4 自适应遗传算法收敛曲线
利用标准遗传算法进行求解,得到最终的混流装配线排序方案为DABCAECAEDACDACAB,目标函数值为39.411 8。其中,标准遗传算法收敛曲线如图5所示。
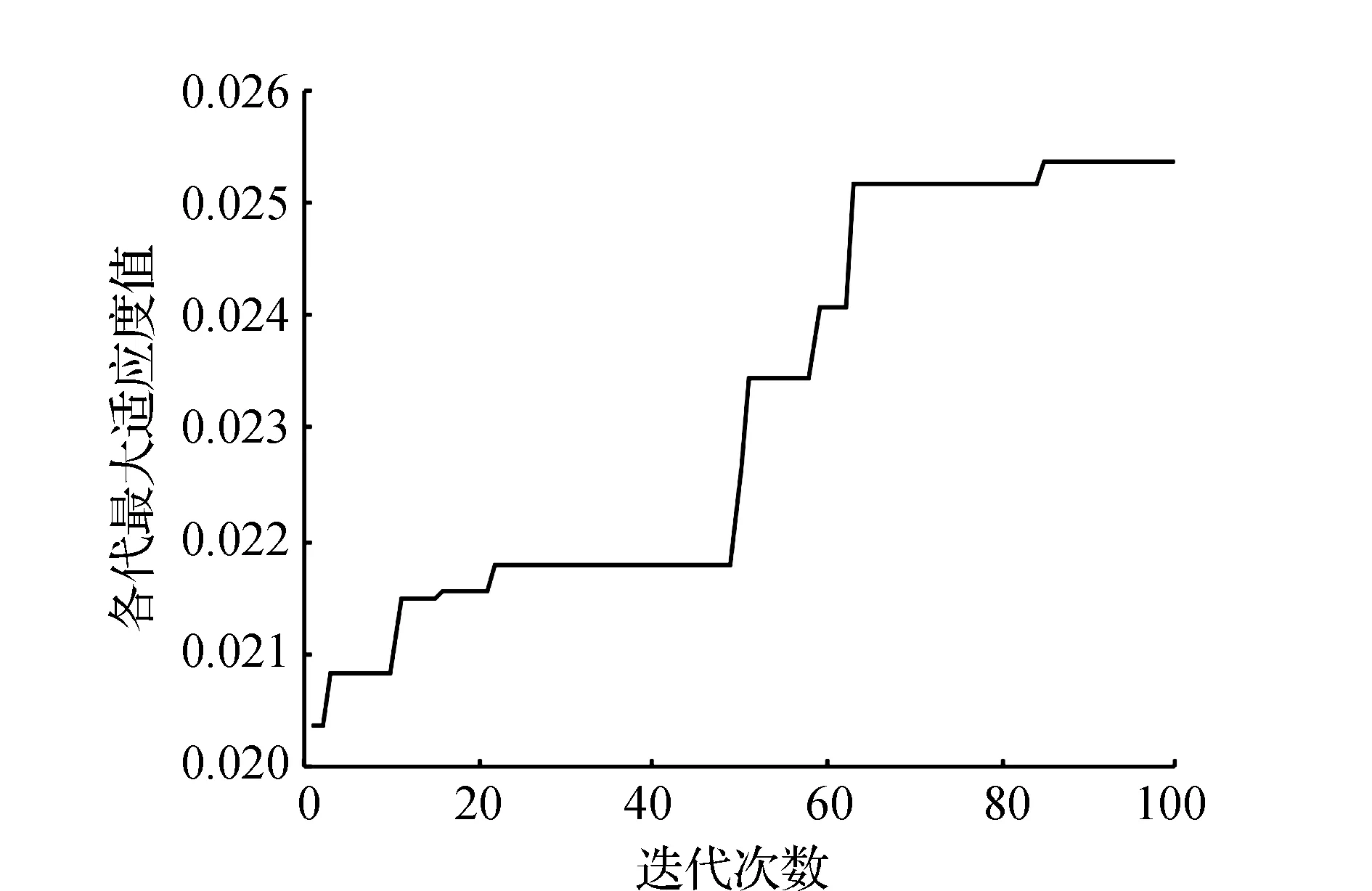
图5 标准遗传算法收敛曲线
通过对比分析两种算法优化性能以及对所构建模型进行求解的最终结果,可以发现,标准遗传算法在迭代85次后收敛,目标函数值为39.411 8。针对同样问题,自适应遗传算法达到稳定状态只需迭代44次,目标函数值为31.282 4,结果表明自适应遗传算法的寻优效果更好,效率更高。
4.2 结果分析
利用本文设计的自适应遗传算法对不考虑零部件均衡重要程度的零部件消耗均衡化模型进行分析,即赋予每种零件相同的权重,可得到对应最优的混流装配线排序方案为DABCAECDACEACABD。比较公司优化前的排序方案以及有无考虑零部件均衡重要程度两种情况优化后的混流装配线排序方案,可得到各零部件的消耗方差值,如表2所示。
由表2可见,相比公司现有的投产顺序,无论采用哪种方式进行优化,都可大幅度降低各类零部件的消耗方差值,可见,使用零部件消耗均衡化模型确定的投产顺序和零部件消耗均衡情况相较于公司现有的投产顺序都会有较大的提升。另外,相比不考虑零部件均衡重要程度的情况,在考虑零部件均衡重要程度的情况下,p5和p6的消耗方差值分别由8.941 2降至6.117 6、12.588 2降至10.764 7,均衡效果分别提升31.578 9%和14.486%,p5,p6二者消耗方差之和由21.529 4降至16.882 3,重要零部件的总体均衡效果提升了21.584 7%。由此可知,基于零部件均衡重要程度的零部件消耗均衡化模型能够优化混流装配线的投产排序顺序,并且可以对生产系统影响程度更为重要的零部件实现更好地均衡,从而优化生产系统,在生产制造过程中实现企业精益生产的目的。

表2 不同排序方案下各零部件的消耗方差值
除此之外,为了最大限度地实现更为重要零件的均衡,造成各类零部件的总体消耗方差之和有所增加,由47.117 6增加至52.882 4。根据制造业的实际生产要求,以牺牲较小的总体消耗波动换取对生产系统影响更为重要的零部件最大限度地均衡是必要且可取的。
4.3 实验分析
为了明确重要零部件消耗均衡与总体波动的关系,以确定对混流装配线所需零部件总体的实质影响,本文根据不同情境设置不同的权重配比方案进行实验分析,如表3所示。

表3 不同的权重配比方案
方案1与方案5对应不考虑零部件均衡重要程度和考虑零部件均衡重要程度两种情境下的解上文已求得,故只需对方案2、方案3和方案4的混流装配线排序进行求解,得到对应的排产顺序分别为DABCAECADACBADEAC、DABCAECADACBAEDCA、DABCAECADBADACECA。根据方案1~5的排产顺序可得到对应的零部件总体消耗方差值分别为47.117 6、49.941 8、50.647 1、51.411 8、52.882 4,其中,重要零部件p5和p6的消耗方差之和分别为21.529 4、20.882 4、20.235 3、18.882 4、16.882 4。通过对方案1~5的总体零部件以及重要零部件消耗方差值进行分析,可以得到不同权重配比方案下各因素的变化曲线,如图6所示。从图中可以看出,自方案1至方案5,随着重要零部件相对重要程度的增强,重要零部件消耗方差和逐渐减少,而总体消耗方差和逐渐增加。由此可以说明,重要零部件消耗均衡化与总体消耗均衡的目标相冲突,更好地均衡重要零部件的消耗是以增加生产系统总体消耗波动为代价的。因此,企业管理者在生产过程中应权衡考虑重要零部件的均衡与总体波动之间的关系,适时为企业管理提供合理决策。
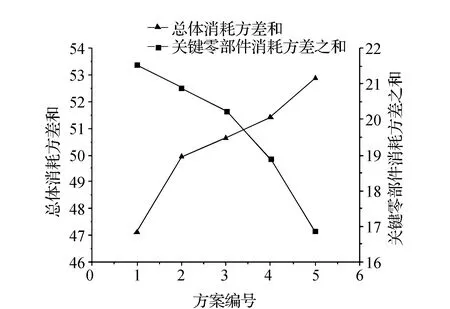
图6 不同权重配比方案下各因素的变化曲线
5 结束语
本文在传统的零部件消耗均衡模型的基础上进行改进,构建了基于零部件均衡重要程度的混流装配线排序模型。根据所建模型,设计了自适应遗传算法,并与标准遗传算法进行对比,结果证明自适应遗传算法的寻优效果更好,效率更高。通过案例的对比分析,证明在各类零部件的总体消耗波动不会显著增加的情况下,基于零部件均衡重要程度的混流装配线排序能够对生产系统影响更大的零部件均衡情况有较大程度地改善。除此之外,通过对重要零部件配比不同的权重方案,证实重要零部件消耗均衡与总体波动之间的关系,对企业管理者合理决策具有借鉴意义。

