博弈模型:体育合作学习发展策略研究

吴本连，吴宗仁，蔡 理

合作学习是我国当前体育课程改革中积极倡导的一种新型学习方式。比较其他学科而言，体育学科的教学更需要合作才能完成的特殊性，决定了合作学习方式在体育教学中的必要性和独特性。因此，体育合作学习方式在体育教学中得到了广泛运用，并且产生了诸多积极效果。但是，由于学界对体育合作学习的学理研究相对不足，不仅导致其形式主义现象的出现，并且出现了一些亟需解决的实际问题，从而制约了体育教学实践发展。

针对存在的实际问题，该研究重点分析体育合作学习中存在的“免费搭车”和“责任扩散”问题，拟从博弈论的角度提出解决对策，以促进体育合作学习的进一步推广和应用。

1 体育合作学习概述

1.1 体育合作学习内涵

体育合作学习是指:在体育教师的组织指导下，学生通过责任分工与密切配合、相互帮助与小组评价等练习策略，实现体育学习目标的一种体育学习方式。体育合作学习对提高学生的学业成绩，心理素质和社会适应能力等有着重要作用。因此，在体育课程论领域，培养学生体育合作学习能力被作为一项重要的课程目标；在体育教学论领域，被视为一种重要的体育教学方法；在体育学习论领域，被看成是一种高水平的体育学习方式。需要说明的是，在体育合作学习过程中，小组奖励、个人责任和成功机会均等是保证体育合作学习产生积极效果的重要前提，体育合作小组中的每位学生都有责任为体育学习任务的完成做出自己的努力。

1.2 体育合作学习研究现状

我国的体育合作学习研究始于1994 年[1]，然而直至2001 年我国新体育课程改革正式启动后，才逐渐增多。代表性研究主要有:李京诚[1]对体育合作学习定义和方法特征进行研究，具有很高的理论价值；潘绍伟[2]强调异质编组形式；毛振明、赖天德[3]揭示了体育自主学习和合作学习的关系；萨出日乐图[4]提出，体育合作学习的教学模式能够促进教学目标高效率达成，有利于学生建立自信心，提高学习效率；陈立伟等人[5]对体育合作学习模式的概念和构建原则进行了剖析等；邱良武[6]通过实验揭示了体育合作学习对提高学生情绪稳定性和课堂满意度的作用，具有较高的借鉴价值。这些研究丰富了体育合作学习的理论体系，对实践具有很好的指导价值。但是，有些观点尚未得到数据验证。张晓健、贾昀昀[7-8]从理论层面对体育合作学习进行了述评，具有一定的参考价值。

国外体育合作学习的研究起步较早于我国，起始于1989 年格里纳斯基[1]对合作性游戏与竞争性游戏效果的比较研究。Dunn S.E[9]指出，进行合作学习，体育教师必须充分了解学生角色与团队，并能制定合理的组织结构。Dyson Ben[10]提出了体育合作学习的五要素，即团队形成、正面影响、个人责任、积极互动和组织处理。为体育合作学习做出了较为详细的分析。Dyson B[11]指出，合作学习在体育教学的过程中具有很大作用，有利于培养学生的创新和实践能力。Dyson Ben[11]指出，教师用任务表指定合作学习的角色，随机选择学生展示他们的能力，通过合作学习发展了个人能力。André Amael[12]进行了残疾人的体育合作学习实验，运动能力得到了提高，产生了积极影响。Victoria A Goodyea[13]指出，体育合作学习能够为学生的学习环境带来积极的变化。

综上而言，体育合作学习在国外近30 年来一直都是学校体育研究中的重要内容之一。比较而言，我国真正兴起的时间晚，发展时间短，侧重理论研究；国外起步早，侧重于实证研究。

1.3 体育合作学习存在的问题

从体育与健康课程目标的四个方面，即运动参与、运动技能、身体健康、心理健康与社会适应来看，体育合作学习能有效促进课程目标的达成。但是，在体育合作学习的实践过程中，经常会出现“免费搭车”和“责任扩散”现象。

由体育合作学习的学理可知:体育合作学习实践中的分组，由于学生个体存在差异，不可避免地会出现组内成员水平参差不齐，因此，会导致在体育学习任务完成的过程中，容易出现由小组中部分甚至个别能力强的学生完成了所有任务，而其他学生却对学习任务漠不关心，这就是“免费搭车”现象。“责任扩散”现象的本意是指，当发生了某种紧急事件时，如果其他人在场，那么在场者所分担的责任就会减小。在进行体育合作学习时，由于有的学生会认为，如果没有完成学习任务的话，一切责任就该由整个小组共同承担，从而导致集体责任泛化分散、相互推诿的消极现象，即“责任扩散”现象。[14]因此，在体育合作学习的教学评价环节，体育教师不仅要客观评价合作小组的学习成果，也要重视评价小组成员在整个合作过程中的个人表现。由于博弈论思想与合作学习具有密切关系，为解决体育合作学习中存在的“免费搭车”和“责任扩散”等问题提供了理论依据。

2 博弈论概述

2.1 “博弈”的提出

博弈一词，如果拆开来看，“博”是指“赌博”，“弈”有对弈，即下棋的意思。下棋在棋局没有完成之前，是遵循一定的对弈规则来决出胜负的。博弈思想历史悠久，早在2500年之前，在《论语·阳货》中，就有“不有博弈者乎”的记载，博，局戏，用“六箸十二棋”；弈，围棋。可见，当时就有“博弈”一说。此外，《孙子兵法》不仅记载过博弈思想，也有许多经典案例，现代博弈思想多受其辩证思维影响。范如国、韩明春在《博弈论》一书中说:博弈是指一些个人、团队或其他组织，面对一定的环境，在一定的约束条件下，依靠所掌握的信息，同时或先后，一次或者多次，从各自可能的行为或策略集合中进行选择并且实施，各自从中取得相应结果或者收益的过程[15]。博弈在英语中与单词“Game”含义相当，Game强调游戏的规则和策略，这与博弈的含义吻合。

2.2 博弈论的发展

博弈论(Game Theor)的发展开始于20 世纪40 年代，代表人物是冯·诺依曼。1994 年，有3 位博弈论专家即数学家纳什(Nash)，经济学家海萨尼(Harsanyi) 和泽尔滕(Selten)，因在博弈论的应用研究上所做出的巨大贡献而获得诺贝尔奖。2005 年，诺伯特·J·奥曼(Robert J.Aumann)和托马斯·C·谢林(Thomas C .Schelling)也因为博弈论的研究而获得诺贝尔奖，他们通过博弈论分析，增加了人们对合作与冲突的深刻理解。现代博弈论的发展，使各个学科领域都发生了翻天覆地的变化，可见，博弈论广泛而深刻地改变了人们的思维方式，有力地促进了多门学科的进步与发展。

3 从博弈论的角度解决“免费搭车”和“责任扩散”现象

3.1 体育合作学习中的“免费搭车”现象

博弈论是研究冲突和对抗条件下对问题提出最优解决策略的理论，是研究竞争的逻辑和规律的理论。通俗地说，博弈论是关于竞争双方或多方的策略选择的学问，又叫对策论。博弈论的许多经典理论都突出了合作的重要性，因此，博弈论与体育合作学习在学理方面密切相关，本研究运用博弈论理论，尝试解决体育合作学习中的”免费搭车”问题是有充分的理论依据的。

1950 年，塔克[16]提出了博弈论经典模型，即囚徒困境。此模型指出，如果每个人都从利己的角度出发，最终结果绝对会对大家都不利，也就是谁也没有占到便宜。纳什在之后提出了又一博弈模型，即“纳什均衡”，纳什均衡是一种策略组合，使得每个参与人的策略是对其他参与人策略的最优反应。如果我们将体育合作学习中的小组学习看成是一种博弈，小组中的每个学生就是一个博弈方。例如，在篮球课的教学或训练中，小组和小组之间进行篮球比赛，各个小组之间就会形成竞争关系。在每个小组内，可能有的学生会想，输赢都是那些能力较强者的事情，与自己关系不大，自己也不会主动参与进来。这种搭便车现象的出现，对于小组的危害和对自己个人的危害都是非常巨大的。

从篮球小组对抗的博弈模型可以看出，小组中篮球技术不好的同学无论是选择出力或者不出力，对于组间对抗的结果似乎影响都不大。输赢的决定因素似乎只在于那些实力较强者。我们可以从表1 看出在组间对抗博弈中的利害关系。[17]

表1 篮球小组对抗下组内成员博弈模型Table 1 The intra-group game model in basketball group match

假设另一小组选择全力以赴，那么在这一小组内，无论弱者选择出力或者不出力，结果都是输或者赢，而强者只要选择不出力，结果就是必输。这样弱者往往选择不出力，将比赛结果交由强者来决定，这也就是现实中体育合作学习出现的免费搭车问题。弱者看似在利害关系中做出了最理性的选择，但是，这种所谓的理性选择对集体是极其不利的。

3.2 博弈论与“免费搭车”问题

在篮球组间对抗的博弈中，体现出了个体理性与群体理性的冲突，即组内每个人在追求个体利益最大化的同时，导致群体利益受损。博弈论中存在着3 种博弈模型，零和博弈、正和博弈和负和博弈。从博弈论的角度来说，搭便车者的这种依附于强者的想法其结果往往会出现负和博弈，个人不受益，小组也失利。在组内往往会出现强者不愿意帮助你，不愿意继续和你合作组成一个小组，而搭便车者也就失去了和别人合作学习的大好机会。可能在小组学习刚开始，强者不论弱者选择合作策略或者不合作策略，强者都会选择与对方合作的策略，那么，在这一阶段，弱者总是选择不合作的策略，会使自己收益最大，弱者肯定想继续留在小组中。但是，对于总是坐享其成的弱者，强者最终肯定会采取不合作策略。可见，弱者的这种选择在合作学习刚开始阶段是成功的，但是，基于这样合作关系的篮球小组，到最后必定是会因为学习效果或比赛成绩不理想，而被淘汰或者更换，当强者被淘汰之后，这个好占强者便宜的“成功者”也必然被淘汰。这就形成了一种“负和博弈”。

在篮球小组学习中，弱者若是一味地不劳而获，强者意识到你的“免费搭车”时，必然会选择和你分道扬镳，喜欢搭便车的弱者一旦暴露身份，强者必然会终止合作关系。不仅导致篮球小组无法获益，也会导致搭便车者再也无法搭到便车。

3.3 体育合作学习中的“责任扩散”现象

“责任扩散”现象是由著名社会心理学家拉塔涅(B.Latane)[16]发现。本意是指，当发生紧急事件时，如果有其他人在场，那么在场者所分担的责任就会减小。李京诚[1]指出，体育合作学习中存在诸多“责任扩散”现象，即学生只对自己的体育学习任务负责，对小组体育学习效果和其他同伴都漠不关心，甚至互相推诿，造成集体责任无人负责的窘境。这是因为，每个学生都认为，一切结果都应由小组所有成员共同承担。例如，在羽毛球教学过程中，运用多球练习法进行小组合作学习时，散落的球会很快布满球场，要求小组成员共同合作，将球全部收拾起来。这时必然出现:有的学生不愿意收球，有的学生处于观望状态，发现别人不收，自己就不收，这样往往会出现两个人甚至多数人相互限制，彼此消极怠工，甚至没有一个人主动收球，必然严重影响学习效果，这就是体育合作学习中经常出现的责任扩散现象。

3.4 博弈论与“责任扩散”问题

羽毛球合作学习中，收球时出现的责任扩散问题，从博弈模型的学理角度来看，体育教师可以选择监督或者不监督，学生可以选择收球或者不收球。假设学生不收球的收益设为D，被体育教师发现不收球而受到处罚设为E，体育教师不监督的收益设为F。那么，体育教师一旦不监督，部分学生选择不收球，那么学生的收益设为D，体育教师的收益就是F-D。当学生选择不收球，体育教师监督发现时，学生可得-E。体育教师可得E.学生收球，体育教师不监督，学生可得0，体育教师可得F，当体育教师监督，学生不收球时，两者收益都为0(见表2)。

表2 羽毛球收球博弈模型Table 2 The game model in badminton receive

在羽毛球合作学习课堂上，部分学生收球还是不收球主要取决于体育教师是否进行监督，体育教师与学生之间相互制约，假定体育教师以P 的概率进行监督，学生以Q 的概率不收球。

对P 进行分析:

当学生选择不收球时，Q=1；当学生选择收球时，Q=0。

Π不收球(1，P)=-E.P+D.(1-P)

Π收球(0.P)=0

如果要让学生收益，也就是不收球也不被体育教师发现，那么我们进行分析:

Π不收球(1，P) >0

即-E.P+D.(1-P) >0

-E.P+D-D.P>0

对Q 进行分析:

当体育教师进行监督时，P=1，当体育教师不监督时P=0。

Π监督(1，Q)=E-E.Q

Π不监督(0，Q)=F-D+D.Q

如果让体育教师收益，即不监督的期望值大于监督的期望值。

即:F-D+D.Q >E-E.Q

我们分析可以发现，体育教师监督的概率P 和学生不收球的概率P 互为函数，即P=Π(Q)，Q=Π(P)，而且当P=，学生都要收球，当，体育教师都要监督。如果两个函数存在一个相交点，也就是两者之间的纳什均衡。

从表2 和图1 可以看出，无论是对P 的分析，还是对Q的分析，都能得出体育教师监督的概率越大，学生不收球的可能性就越小。所以，重点是要增大E 的值，即加大对部分不收球学生的处罚力度。

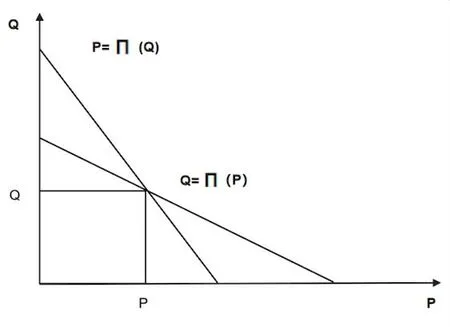
图1 羽毛球收球博弈体育教师和学生的纳什均衡Figure 1 Nash Equilibrium between Physical Education Teachers and Students in Badminton Ball Reception Game

团队合作学习中，对于公共任务的完成，总有些学生试图等待其他人做出行动，自己则坐享其成。在遇到每个参与方都以“等待者”自居时，学习活动将无法继续进行，集体任务也无法顺利完成。对于体育教学中出现的责任扩散现象，体育教师应当及时采取相应措施，向参与方说明这种做法的错误和危害；同时，也应当发挥体育教师的主导作用，要求每个学生都参与到体育学习活动中来，集思广益、群策群力地完成团队任务。例如，在羽毛球的多球合作练习中，体育教师务必及时要求学生在收球时都要积极快速进行，并且一定要对不合作者采取一些惩罚的措施。同时，体育教师要注重提高学生的体育合作技能，在出现责任扩散时，体育教师要及时教育学生，使他们时刻具有完成集体任务的使命感。

4 结语

博弈论的学理价值博大精深，体育合作学习的独特作用毋庸置疑。“免费搭车”和“责任扩散”现象既是体育合作学习中普遍存在的，也是可以运用博弈学理避免的。但是，负和博弈是与体育合作学习背道而驰的。因此，务必运用纳什均衡模型，努力促进正和博弈形成，这也是体育合作学习的最高追求。