求解非线性方程组的Newton 型方法研究

徐 浩 司智勇

(1- 河南理工大学数学与信息科学学院，焦作 454000;2- 燕山大学信息科学与工程学院，秦皇岛 066000)

1 引言

Newton 迭代法是求解非线性方程组的一个重要方法，目前使用的很多其他类型的迭代法都是以Newton 法为基础，在其上延伸与拓展之后得到的.研究Newton 型迭代法对现代非线性方程组的研究具有重要意义[1,2].本文利用文献[3]的思想，结合非线性方程组的数值解法对现有的迭代法进行改进，得到了四类新的Newton 型迭代方法.数值实验表明，这四种迭代算法比Newton 法收敛速度更快.

2 格式的构造

设F(x):D ⊂Rn →Rn，考虑非线性方程组

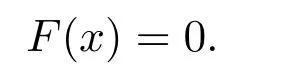
求解此类非线性方程组最基本的方法就是Newton 迭代法，Newton 迭代法是一个既简单又十分重要的方法.它的迭代格式为

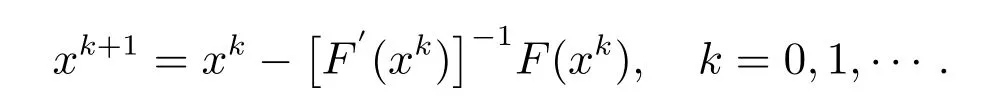
以上为Newton 迭代法的n维迭代格式.

求解非线性方程的Newton 法是

文献[3]中给出了一种求解非线性方程Newton 迭代法的改进，迭代格式为，对r ∈[1/2,1][3,4]：

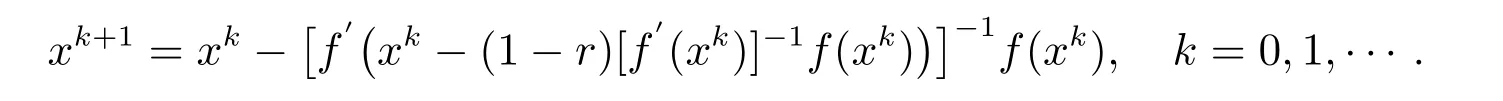
从几何[5]上来看，这种迭代方式是将Newton 法中(xk,f(xk))点的切线改变成了另外一点

的切线，使得收敛速度更快.于是，我们将其直接推广到n维，可以得到以下迭代方式，对r ∈[1/2,1]：

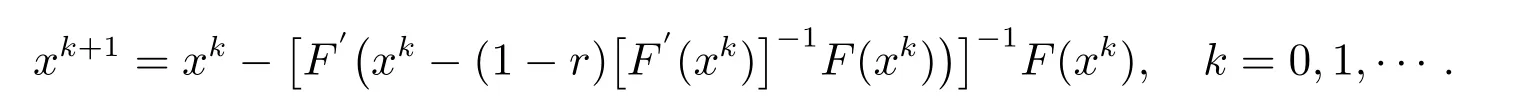
以上则为文中求解非线性方程组的第一种Newton 型迭代格式.此种方法相较于Newton 迭代法而言，每次迭代需要多求一次逆矩阵.虽然能加快收敛速度，但是计算量巨大.这种迭代方法对非线性方程适用，对于求解非线性方程组很可能计算量太大导致无法进行.

简化的牛顿方法[6]又给了我们一种新的思路，就是以F′(x0)来替代F′(xk)，达到简化运算的目的，即除了第一次需要求两次逆矩阵之外，后面迭代都只需要进行一次逆矩阵的计算.迭代效果来说，会相较文中第一种差.这种算法和Newton 迭代法的计算量基本相同，要比Newton 法要快.下面给出文中第二种迭代格式(r ∈[1/2,1])：

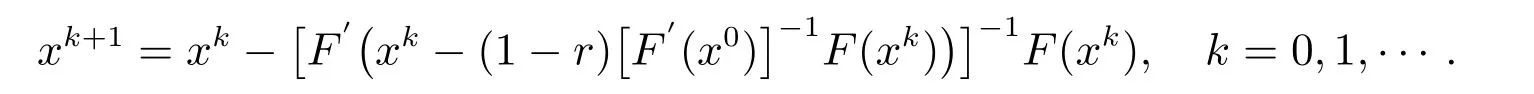
对上文进行总结得出一般式

1)A=[F′(xk)]-1时，为Newton 迭代方法.

2)A=[F′(xk-(1-r)[F′(xk)]-1F(xk))]-1, k=0,1,···为文中第一种方法.

3)A=[F′(xk-(1-r)[F′(x0)]-1F(xk))]-1, k=0,1,···为文中第二种方法.

3 基于修正Newton 法的改进

求解非线性方程组的修正Newton 迭代法为

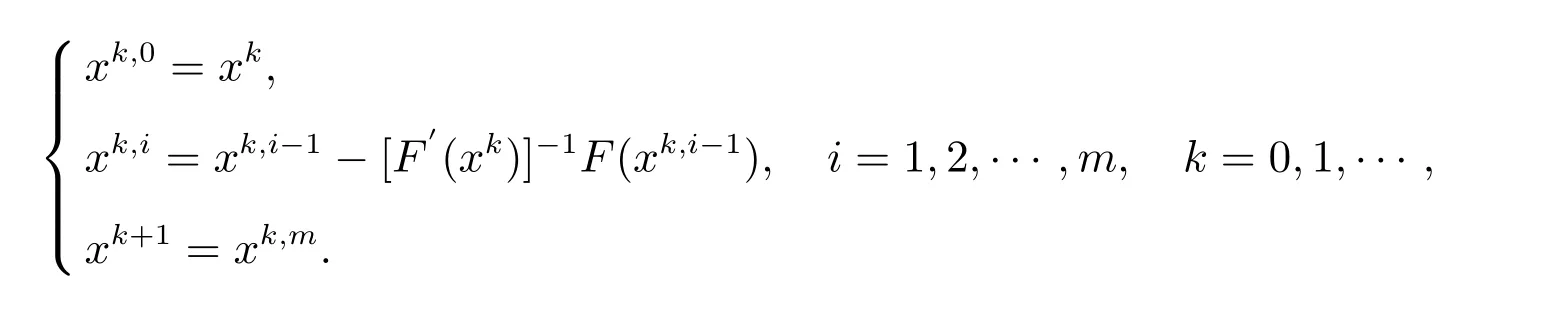
它具有m+1 阶敛速[6].取m=2，则有

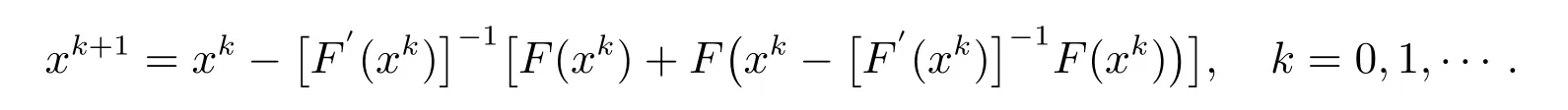
于是，将此法与文中第一种方法结合，即可出现一种新的迭代方式

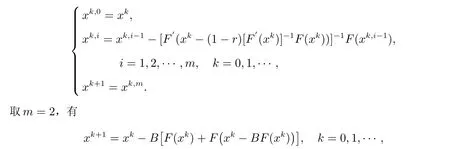
其中B= [F′(xk-(1-r)[F′(xk)]-1F(xk))]-1.相较于修正Newton 法而言，虽然增加了运算量，但收敛速度更快.此为文中第三种迭代方法，得益于简化的牛顿方法.为了减少运算量，我们马上又可以得到文中第四种迭代方式，即将B中[F′(xk)]-1替换为[F′(x0)]-1，即可得到文中第四种迭代方法

综上，得到一般式

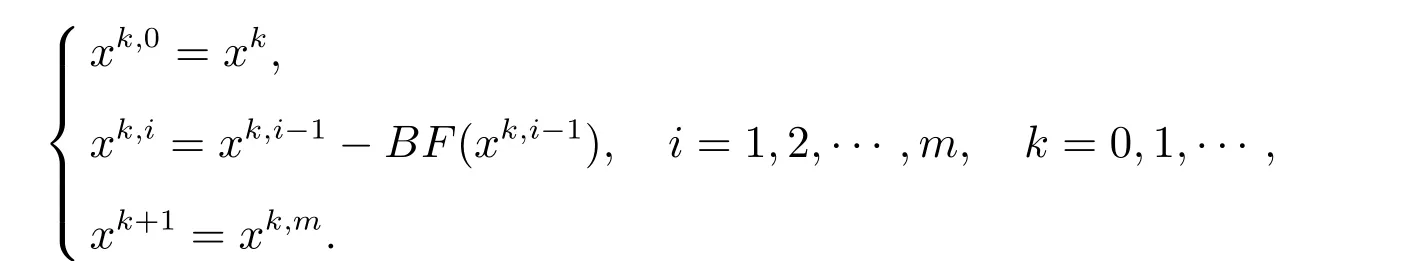
1)B=[F′(xk-(1-r)[F′(xk)]-1F(xk))]-1时：

(a)m=1, r=1，此法即是Newton 法；

(b)m/=1, r=1，此法即为修正Newton 法；

(c)m=1, r/=1，此法即为文中第一种方法；

(d)m/=1, r/=1，此法为文中第三种方法.

2)B=[F′(xk-(1-r)[F′(x0)]-1F(xk))]-1时：

(a)m=1, r=1，此法即是Newton 法；

(b)m/=1, r=1，此法即为修正Newton 法；

(c)m=1, r/=1，此法即为文中第二种方法；

(d)m/=1, r/=1，此法为文中第四种方法.

4 算法分析

定理1(Newton 型迭代法的收敛定理)[6]假定F:D ⊂Rn →Rn在凸集D0⊂D上F可导，且满足

成立，则对任何x,y ∈D0，有

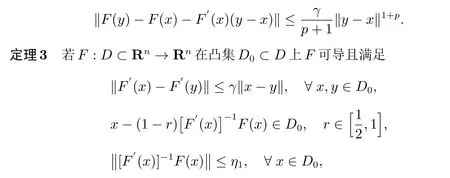
则

对任意的x ∈D0满足

其中μ, δ0, δ1≥0.

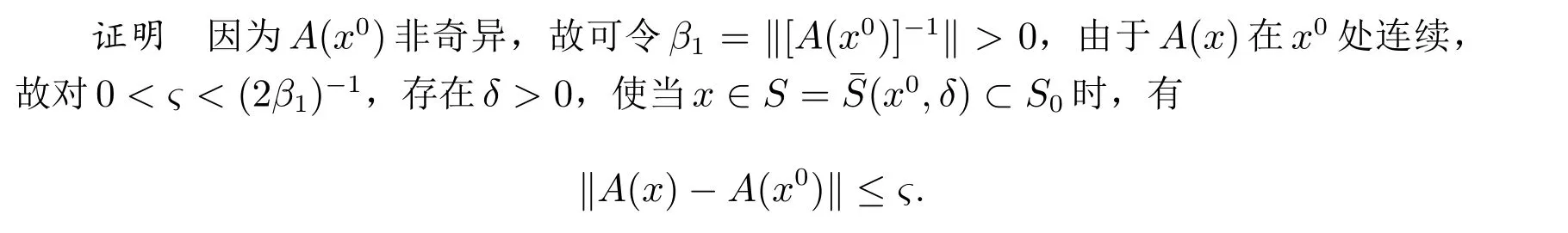
再由F在x0处F可导，故可选充分小的δ ＞0，使对任何x ∈S= ¯S(x0,δ)，有

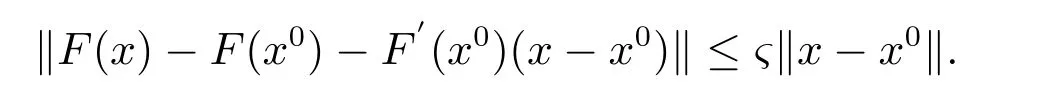
又因为‖F′(x)-F′(x0)‖≤γ‖x-x0‖, ∀x ∈S，所以由定理2 可知

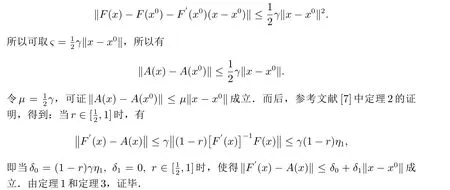
定理4 若F:D ⊂Rn →Rn在凸集D0⊂D上F可导且满足

则

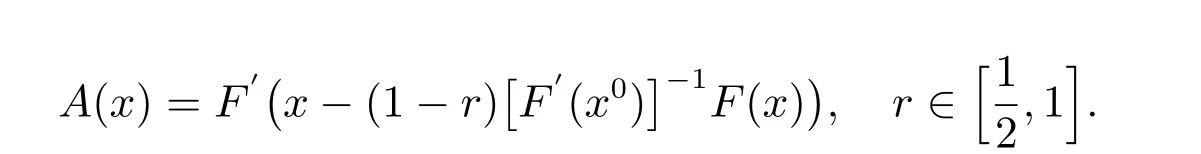
对任意的x ∈D0满足

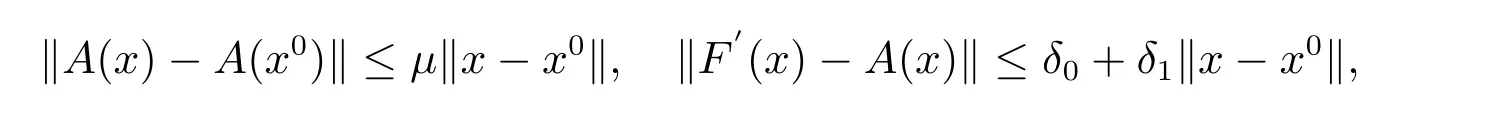
其中μ, δ0, δ1≥0.

证明 因为A(x0)非奇异，故可令β1=‖[A(x0)]-1‖ ＞0，由于A(x)在x0处连续，故对0＜ς ＜(2β1)-1，存在δ ＞0，使当x ∈S= ¯S(x0,δ)⊂S0时，有

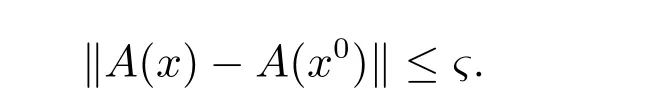
再由F在x0处F可导，故可选充分小的δ ＞0，使对任何x ∈S= ¯S(x0,δ)，有

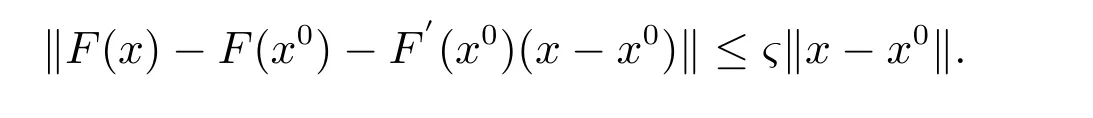
又因为‖F′(x)-F′(x0)‖≤γ‖x-x0‖, ∀x ∈S，所以由定理2 可知

成立，则称序列xk至少p阶收敛.

定理6 假定F:D ⊂Rn →Rn在x*的开邻域S0⊂D上F可导且F′(x*)非奇异，而x*为F(x)=0 的解，则存在闭球S= ¯S(x*,δ)⊂S0(δ ＞0)，使映像

对所有x ∈S有定义，且文中第一种方法生成的序列xk超线性收敛到x*.若还假定

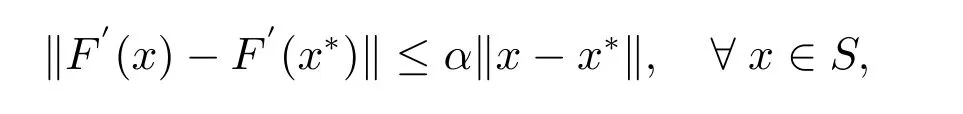
α ＞0 为常数，则文中第一种算法的序列xk至少二阶收敛.

证明 在定理5 中取A(x)=F′(x-(1-r)[F′(x)]-1F(x))，则映像

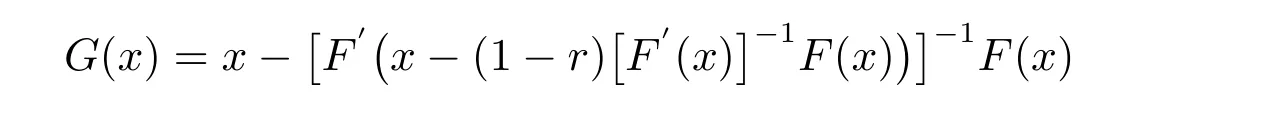
在球S ⊂S0上有定义且

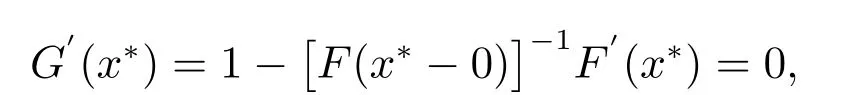
于是ρ(G′(x*))=0＜1.由定理4 知xk收敛到x*且当xk/=x*, k ≥k0时，有

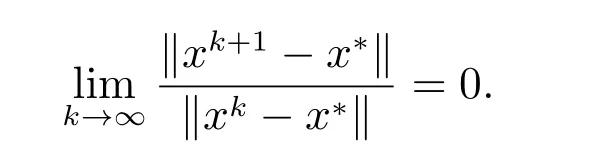
所以，文中第一种Newton 型迭代法是超线性收敛的.由定理2 可知

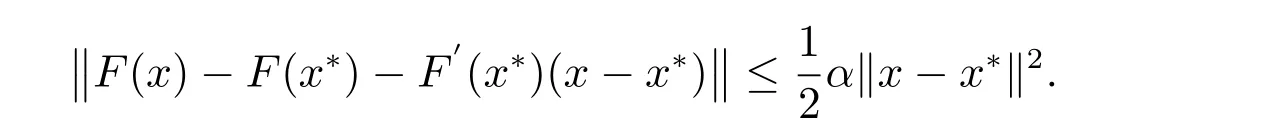
于是有

因为F′(x*)=A(x*)，所以得到以下表达式

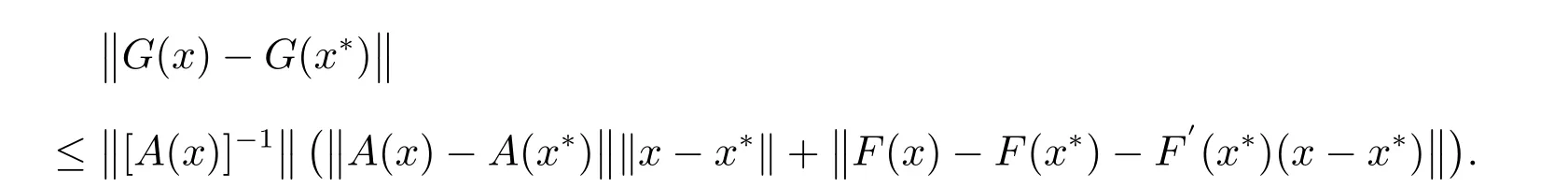
取β=‖[A(x*)]-1‖ ＞0，由于A(x)在x*处连续，故对0＜ς ＜(2β)-1，当x ∈S=¯S(x*,δ)⊂S0时，有‖A(x)-A(x*)‖≤ς，由摄动引理可知对x ∈S,[A(x)]-1存在，且

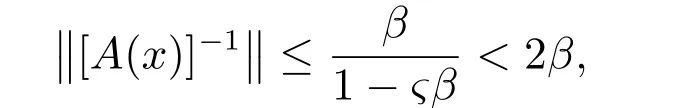
F在x*处F可导，故可选充分小δ ＞0，对任给x ∈S= ¯S(x*,δ)，有

α ＞0 为常数，则文中第二种算法的迭代序列{xk}至少二阶收敛.

证明 在定理5 中取A(x)=F′(x-(1-r)[F′(x0)]-1F(x))，则映像

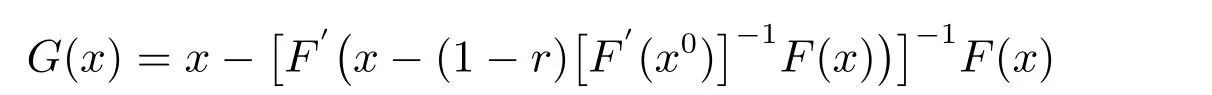
在球S ⊂S0上有定义且

于是ρ(G′(x*))=0＜1.由定理4 知xk收敛到x*且当xk/=x*, k ≥k0时，有

所以，文中第二种Newton 型迭代法也是超线性收敛的.由定理2 可知

于是有

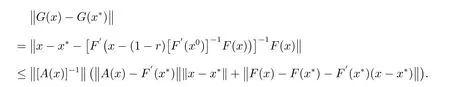
因为F′(x*)=A(x*)，所以得到以下表达式

F在x*处F可导，故可选充分小δ ＞0，对任给x ∈S= ¯S(x*,δ)，有

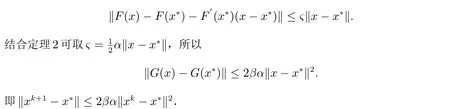
由定义1 可知文中第二种方法收敛阶至少为2.

定理8[6]若序列{xk}⊂Rn超线性收敛于x*，当k ≥k0时，xk/=x*，则

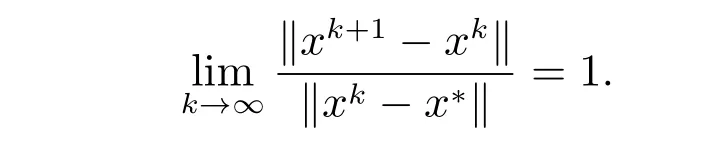
定理9 若F:D ⊂Rn →Rn在x*的邻域S(x*,δ)⊂D上F可微，且F′(x*)非奇异，x*是F(x)=0 的解，再假定对任何x ∈S，存在正常数γ，使

成立，则x*是文中第三种迭代方式生成序列{xk}的吸引点，且

同时，类推可有

证明 由定理6 可知映像

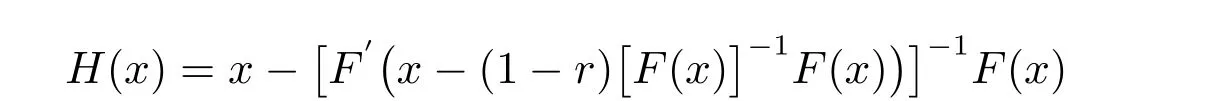
在球S1= ¯S(x*,δ1)⊂S上有定义并满足

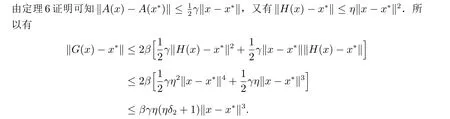
取c1=βγη(ηδ2+1)，它是一个不依赖k的常数，当xk+1=G(xk)时，则有

即文中第三种方法当m= 2 时收敛阶至少为3，类推即可证明文中第三种方法收敛阶至少为m+1.由定理8 可知‖xk,2-x*‖≤c1‖xk-x*‖3，于是

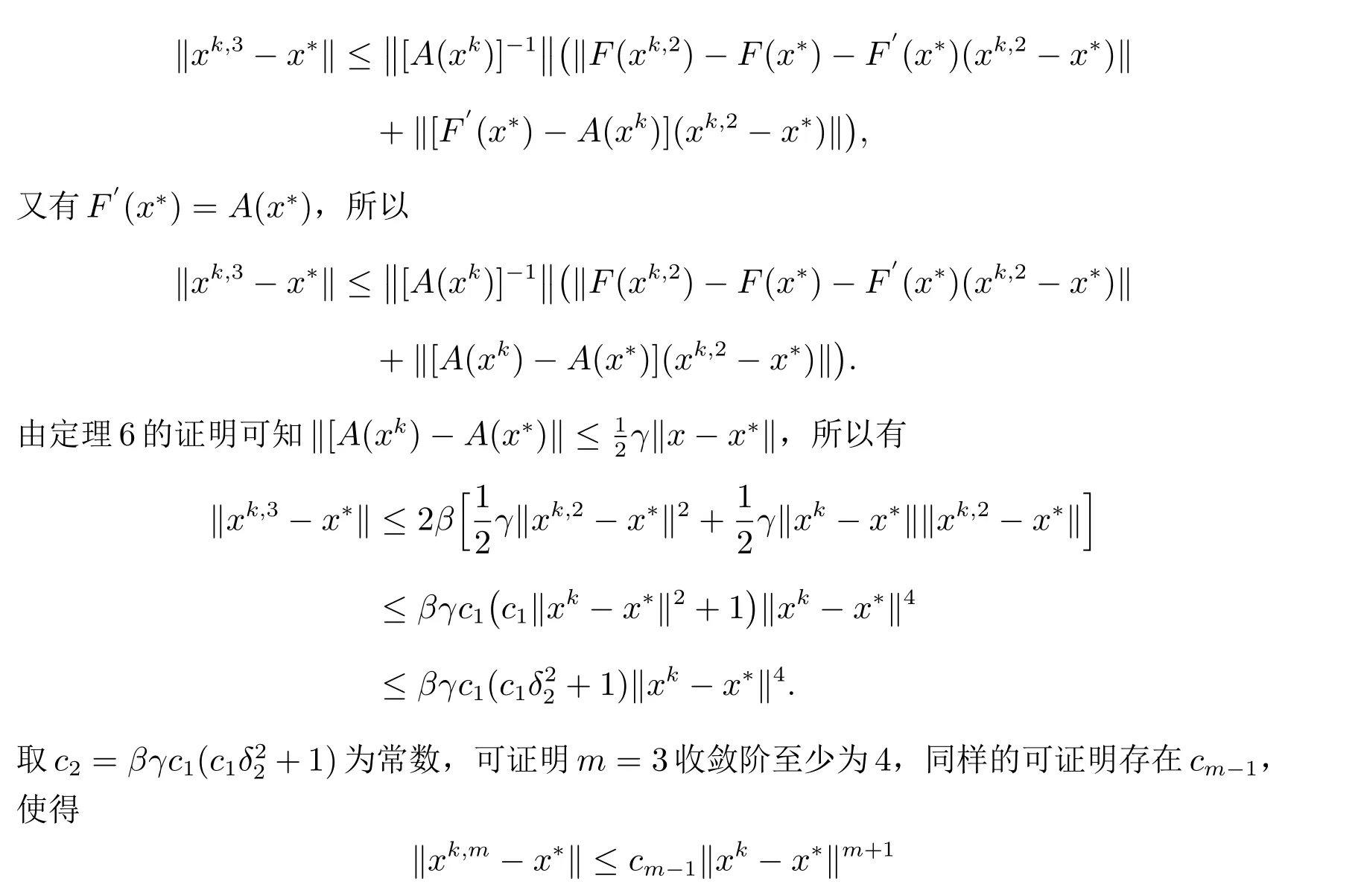
成立，即文中第三种方法至少m+1 阶收敛.

定理10 若F:D ⊂Rn →Rn在x*的邻域S(x*,S)⊂D上F可微，且F′(x*)非奇异，x*是F(x)=0 的解，再假定对任何x ∈S，存在正常数γ，使

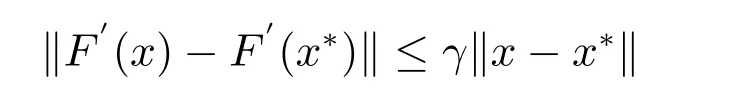
成立，则x*是文中第四种迭代方式生成序列{xk}的吸引点，且

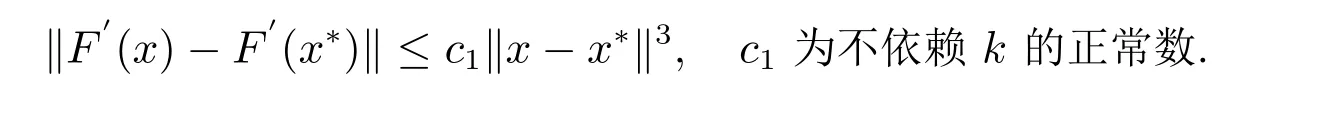
同时，类推可有

证明 由定理7 可知映像

在球S1= ¯S(x*,δ1)⊂S上有定义并满足

取c2=βγη(ηδ2+1)，它是一个不依赖k的常数，当xk+1=G(xk)时，则有

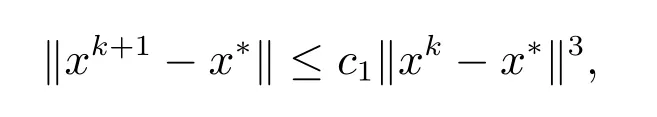
即文中第四种方法当m= 2 时收敛阶至少为3，类推即可证明文中第四种方法收敛阶至少为m+1.由定理8 可知‖xk,2-x*‖≤c1‖xk-x*‖3，于是又有F′(x*)=A(x*)，所以有

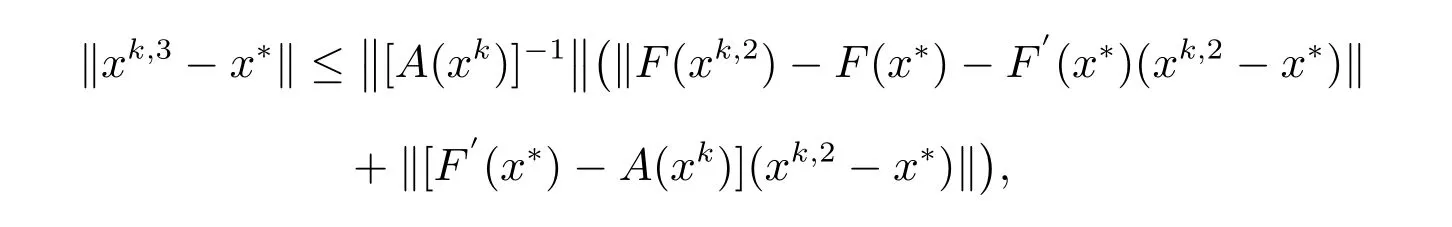
成立.即文中第四种方法至少m+1 阶收敛.

5 数值实验

在本节中，我们给出一些数值实验结果，表明我们的算法的有效性和优点.

例1

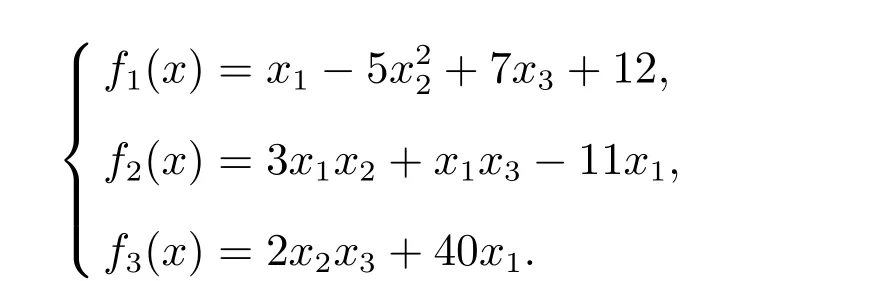
我们取初值x0=(108,109,9)T.几种迭代法的数值实验结果如表1 至表5 所示.

表5 文中第二种方法的数值结果(取r =2/3)

表1 Newton 法的数值结果

表2 文中第一种方法的数值结果(取r =1/2)

表3 文中第一种方法的数值结果(取r =2/3)

表4 文中第二种方法的数值结果(取r =1/2)

由于文中第一、二种方法是在牛顿法基础上进行拓展，所以我们将第一、二两种算法与牛顿法分别进行比较.我们观察表格发现r取值不同，算法迭代收敛的真解也不同，这是因为r影响着算法的收敛速度，会出现初值相同但贴近不同真解的情况.从数值结果中可以发现两种方法相较于牛顿法的36 步迭代步数均要少.同时，我们记录了算法运行的时间，如表6 所示.

表6 几种算法的计算时间

由于文中第一种方法(取r= 2/3)和文中第二种方法(取r= 1/2)的真解与牛顿法真解不同，所以与牛顿法的结果进行比较时无参考价值.我们看其他两种都比牛顿法得出结果速度要快.

将第一种与第二种方法进行比较，选取初值条件x0= (98,99,9)T, r= 1/2.发现文中两种方法与牛顿法有相同真解(-0.4151,2.6039,3.1882)T.

由表7 可以发现，第一种方法较第二种方法迭代步数较少，计算时间较长.第二种方法迭代步数较多，计算时间较短.由此我们发现文中的算法当迭代步数与牛顿法相差较大的时候，文中两种算法得出结果速度较快.而当迭代步数与牛顿法相差不大的时候，文中两种方法得出结果速度与牛顿法持平甚至较牛顿法收敛慢，且文中第一种方法稍慢于文中第二种方法.

表7 r 取1/2 时文中第一、二种方法同Newton 法的迭代步数和计算时间

下面为修正牛顿法及由其拓展得出的文中第三、四种方法：取初值x0=(108,109,9)T，详见表8 至表12.

表12 文中第四种方法数值结果(取r =2/3)

表8 修正Newton 法收敛结果

表9 文中第三种方法数值结果(取r =1/2)

表10 文中第三种方法数值结果(取r =2/3)

表11 文中第四种方法数值结果(取r =1/2)

由于文中第三、四种方法是在修正牛顿法基础上进行拓展，所以我们将第三、四种方法与修正牛顿法分别进行比较.由于r= 1/2 时三种方法真解不同，所以我们取r=2/3 的数据进行比较.表13 为迭代步数及运行时间的对比.

表13 r 取2/3 时文中第三、四种方法与修正牛顿法的迭代步数和计算时间

由表13 我们可以看出，文中第三、四种方法迭代步数和得出结果时间均优于修正牛顿法.我们再取初值条件为x0= (45,96,9)T，进行实验三个算法为相同真解(0,1.5492,0)T，表14 为三个算法对比.

表14 r 取1/2 时文中第三、四种方法与修正牛顿法的迭代步数和计算时间

同样的，我们发现迭代步数相差不大的时候文中第三种方法也较修正牛顿法稍慢，而第四种稍快一点.由此我们得出结论，初值条件离真解较远时，迭代步数较多，用文中第一、三方法更合适.而初值条件离真解较近时，迭代步数相差不多，用文中第二、四方法或者牛顿法与修正牛顿法更合适.下面我们来看看高阶非线性方程组中四种方法的情形.

例2

由表15 我们可以得出类似的结论，即文中第一、三种方法加快了收敛速度，使得迭代步数相较传统的Newton 法与修正Newton 法而言较少.而文中第二、四种方法在一、三方法的基础上，从节省计算量的角度出发，虽然放慢了收敛速度，但同时加快了运行速度.得出真解的速度比传统的Newton 法与修正Newton 法更快.

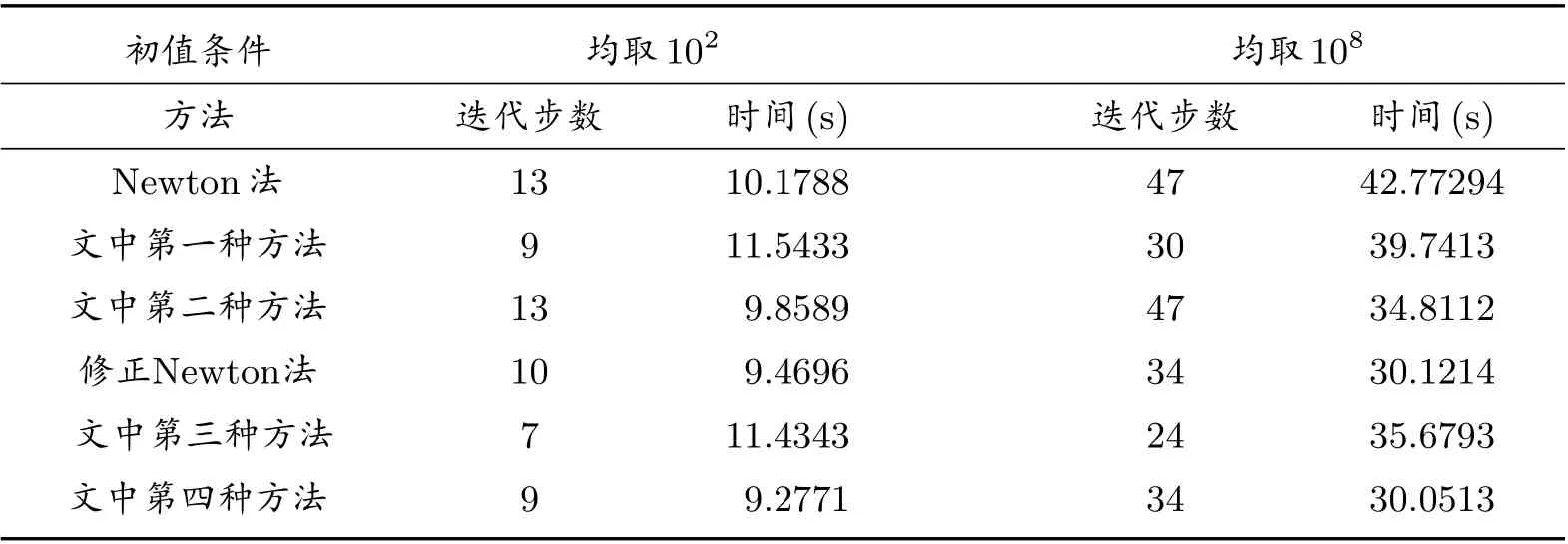
表15 迭代步数和计算时间(文中四种方法r 均取1/2)