缺失数据环境下汇率序列的潜变量Metropolis-Hastings算法及触发式理财产品定价
董 艳
(陕西铁路工程职业技术学院基础部,渭南 714000)
1 引言
在众多行业里,不间断地连续营业是不现实的,金融业亦是如此,从而许多金融数据,常常出现数据缺失现象.图1 给出了2018 年9 月20 日至9 月27 日的欧元兑美元汇率的开盘价,由于周末不开盘,出现了48 小时的数据缺失.符合此情形的案例还有很多,国内上交所和深交所各种股票和指数均在周末和节假日闭盘.
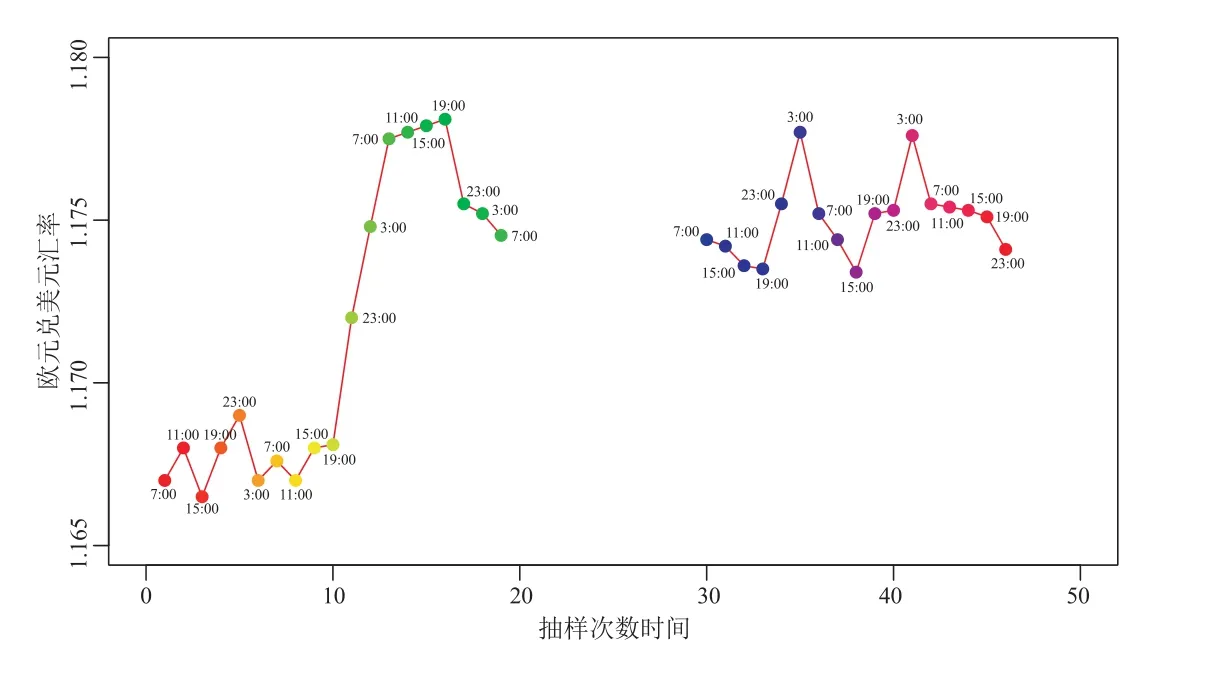
图1 2018 年9 月20 日至9 月27 日的欧元兑美元汇率
数据的缺失不但会影响投资者对市场的判断,还给金融序列的预测增加了难度.虽然一级市场上的金融活动在闭盘期间已经停止,由于次级市场受监管的程度较小,其金融活动仍持续进行,且此部分数据并不能被有效搜集.文献[1,2]已经证实忽略缺失值、仅采用营业时间获取的金融数据进行估计常常会低估波动率.这提示我们必须采用某些缺失值的替补方案进行插值.
当前可用于缺失数据替补的方法有很多,总体来看,主要包括均值替代法[3-5]、聚类分析法[6,7]、关联规则法[8,9]、阀值填补法[10]、回归填补法[11]以及多重插补方法[12].但综合分析这些方法,仍然存在以下几个问题:第一,大多数方法,没能考量填补数据对总体分布的影响,如均值替代法和基于线性回归的填补方法;第二,有些方法对基于特定的分布的样本数据有效,将其推广至时间序列是困难的,例如聚类分析法和关联规则法.
目前,基于贝叶斯的马尔科夫链蒙特卡罗(MCMC)抽样方法的时间序列研究是统计学的热点之一.文献[13]利用二项算子并结合MCMC 模拟研究了一种推广的ARMA 过程.文献[14]采用数据扩充法、切片抽样法以及MCMC 方法,给出了具有稳定分布噪声的ARMA 模型更为简洁、有效的贝叶斯建模方法.文献[15]则用MCMC 模型选择考察了ARMA 模型的阶数问题.在工程实践方面,文献[16]通过收集1994 年第1 季度至2009 年2 月10 日的国际原油Brent 价格的时间序列数据,并对其建立了ARIMA(p,d,q)模型.在ARMA 模型参数估计上,文献[16]在Winbugs 软件平台上运用MCMC 方法进行了参数估值运算,得到Brent 原油季度价格ARIMA(1,1,1)模型的模拟结果.
基于以上分析,本文提出一种潜变量Metropolis-Hastings(M-H)抽样方法、在缺失数据情形下,研究ARMA 汇率模型的参数估计问题,该方法综合考量了填补数据对序列分布、自相关性的影响.模拟结果表明:相比于传统Gibbs 方法,潜变量M-H 方法产生的抽样序列不存在波动聚集现象.
2 汇率模型及假设
本文考察挂钩于汇率的触发式理财产品定价问题.假设汇率过程xt遵循

其中r0表示汇率长期水平,汇率的对数序列yt具有均值为0,且有ARMA 模型形式
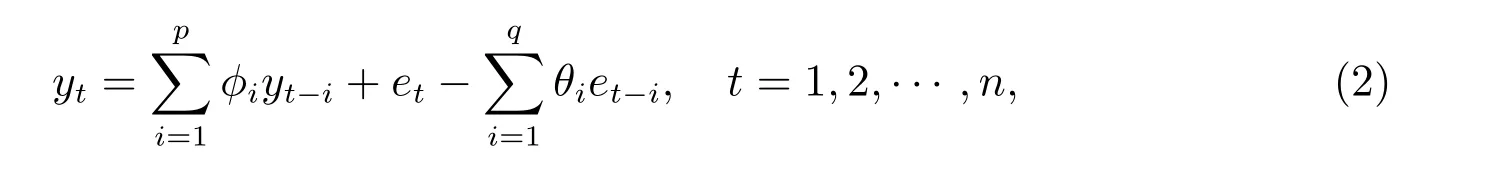

这里m0=m2-m1, m2>m1.考虑时间序列模型的稳定性,假设|φ|<1,并且模型的先验分布设置如下:
1) 假设自回归系数φi(i=1,2,··· ,p)和滑动平均系数θi(i=1,2,··· ,q)服从(-1,1)上的均匀分布,那么它们的密度函数为
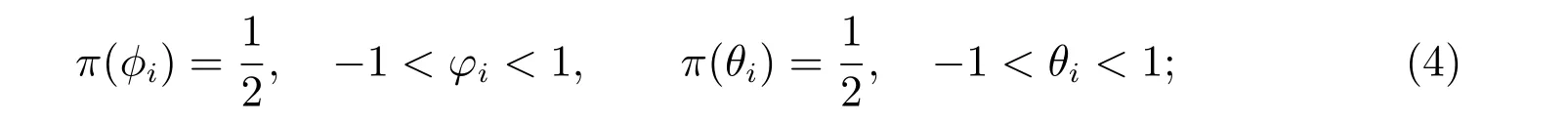
2) 假设随机误差项的方差σ2~IGA(α,β),即σ2服从参数为α和β的逆伽马分布,其密度函数为
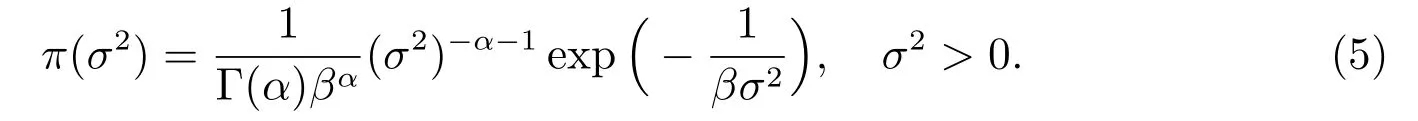
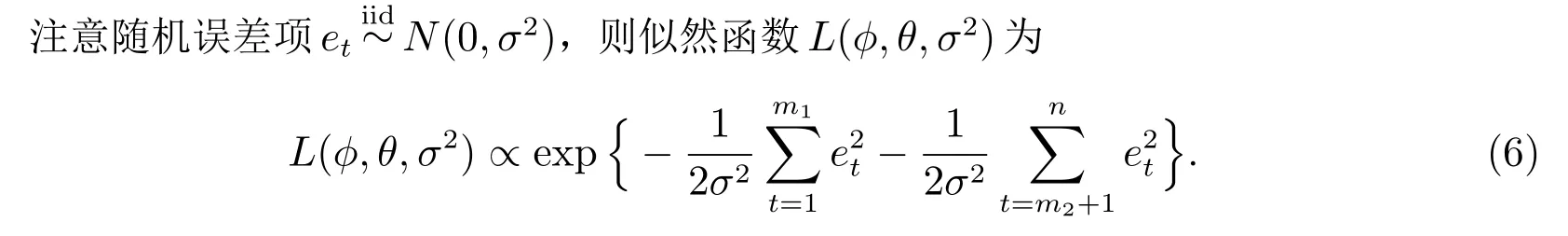
同时,为了方便论述定义随机误差项
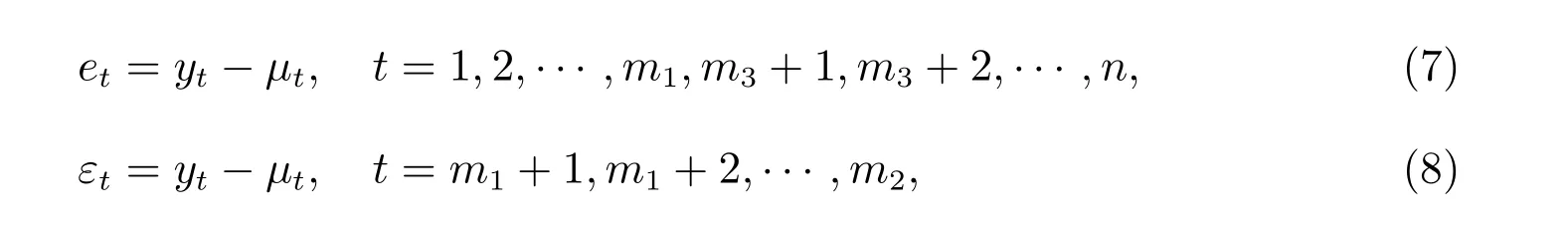
其中
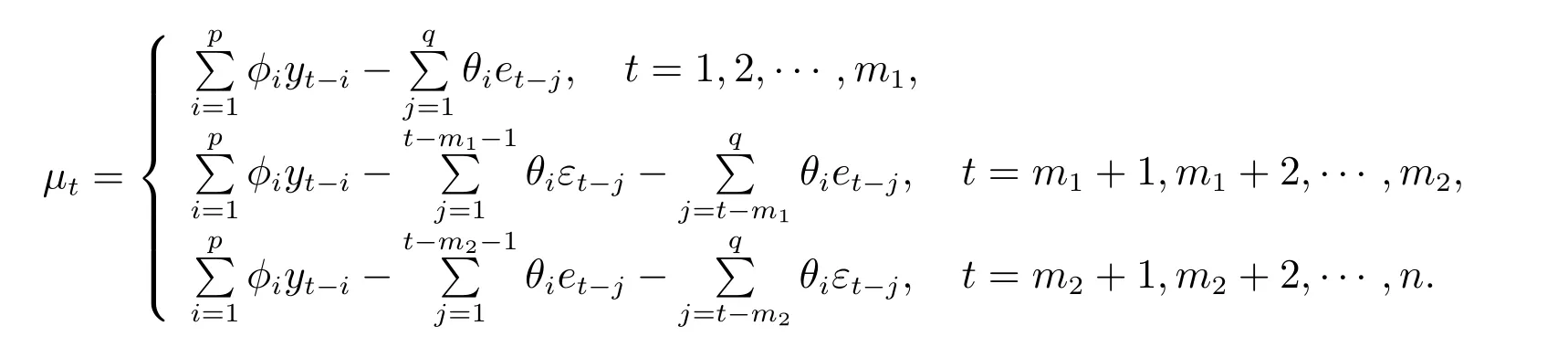
考虑到当t=m1+1,m1+2,··· ,m2时,yt为缺失值,从而在公式(7)—(8)用et和εt区别对待随机误差项.这也意味着中间m0个缺失值ym1+1,··· ,ym2可以采用下面的公式插补
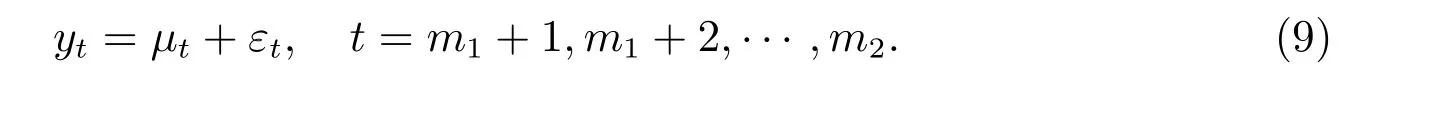
3 数据插补和后验分布
本节在构造一种潜变量数据插补方法之后,分析相应的共轭后验分布,以便之后进行M-H 抽样.注意插补数据的目的并不是预测单个缺失值,而是预测缺失数据所服从的分布.通过数据的插补,既要克服数据缺失带来的不便,同时又不能改变原有的数据分布.据此,本文依据文献[17]构造潜变模型,采用潜变量方法弥补缺失部分对应的随机误差项

则全数据似然函数为
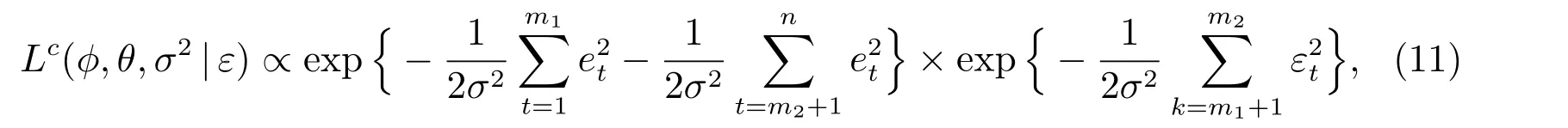
它满足
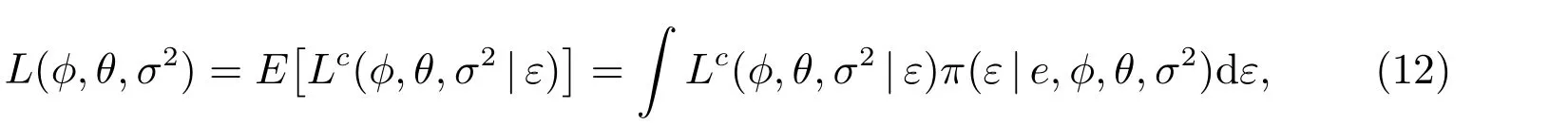
其中
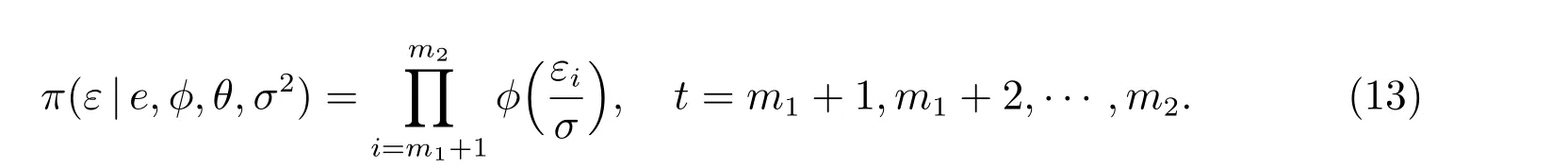
接下来,构造参数φ, θ, σ2的后验分布,并根据此后验分布获取参数的Gibbs 抽样序列.已知时间序列{y-p+1,··· ,y-1,y0,y1,y2,··· ,yn}和各个参数的先验分布后,由贝叶斯定理可得参数的后验分布为
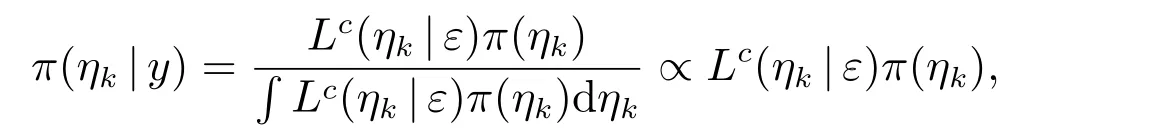
其中ηk表示参数向量η={φ,θ,σ2}中的任一参数.下面不加证明地给出潜变量情形下的几个有关后验分布的结果,其证明过程可以类推不附加潜变量情形的证明[15,17],这里不再赘述.
推论1 设φ-i表示自回归系数向量φ除去φi以外的部分,i=1,2,··· ,p,则其后验条件分布满足
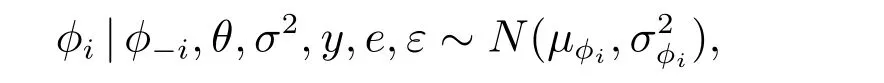
其中
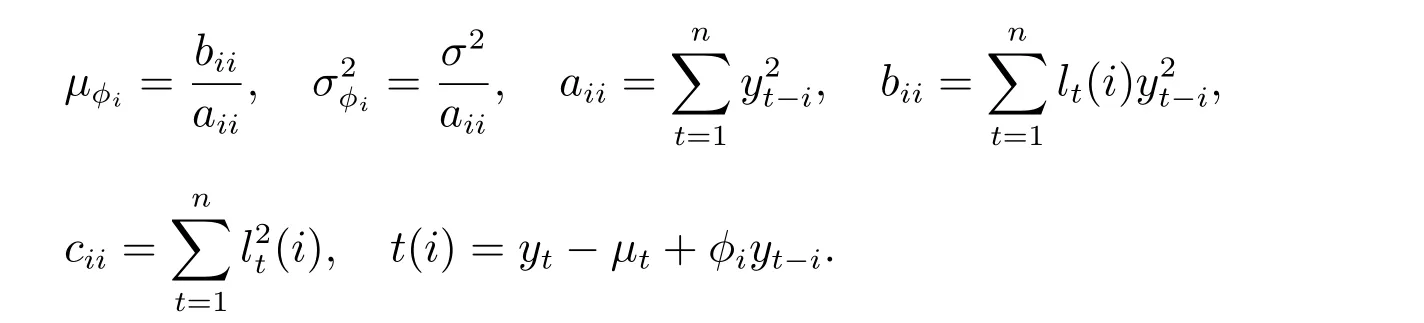
推论2 在假设(5)下,白噪声的方差σ2的先验分布共轭,且
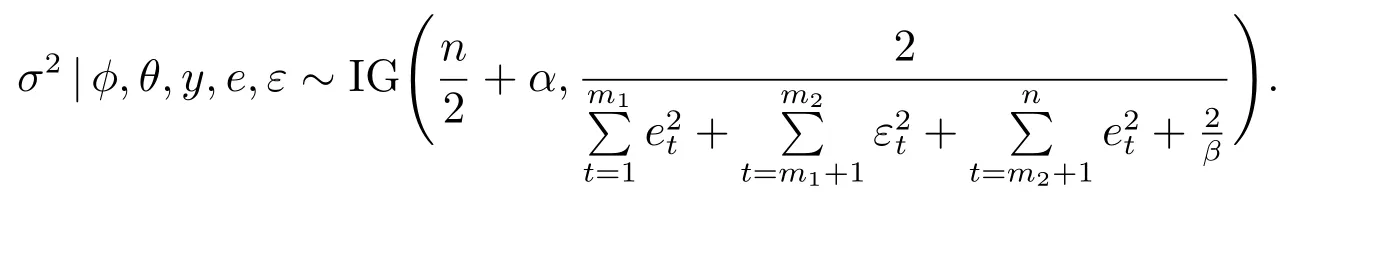
在接下来的章节中,将采用基于潜变量M-H 抽样的MCMC 算法研究汇率序列的参数估计.
4 潜变量M-H 抽样

考察Markov 链抽样序列的平稳性,如果具有转移矩阵P和分布π(φi)的Markov 链对所有的状态θi, θj满足下面的等式
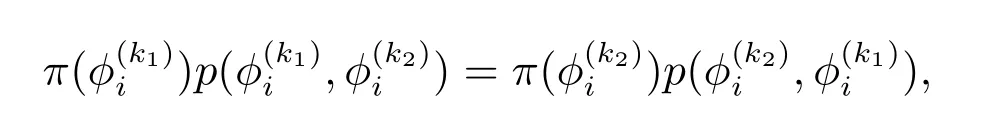
上式称为细致平衡方程,此时该马氏链的分布π(x)是平稳的.

那么
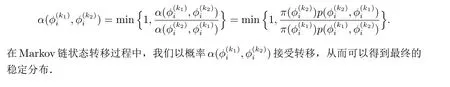
本节采用独立Markov 链,其转移概率与当前状态无关,则
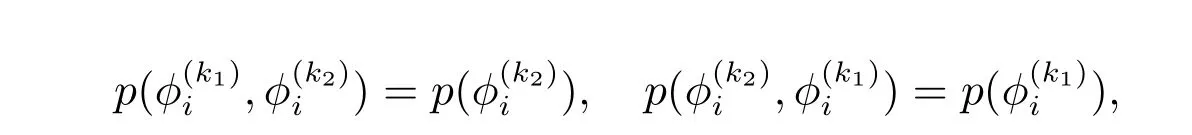
从而自回归系数的MCMC 采样方法分为以下几个步骤:

则公式(2)可以写成
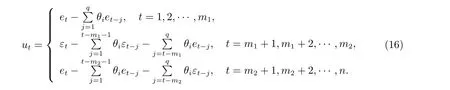
定义序列
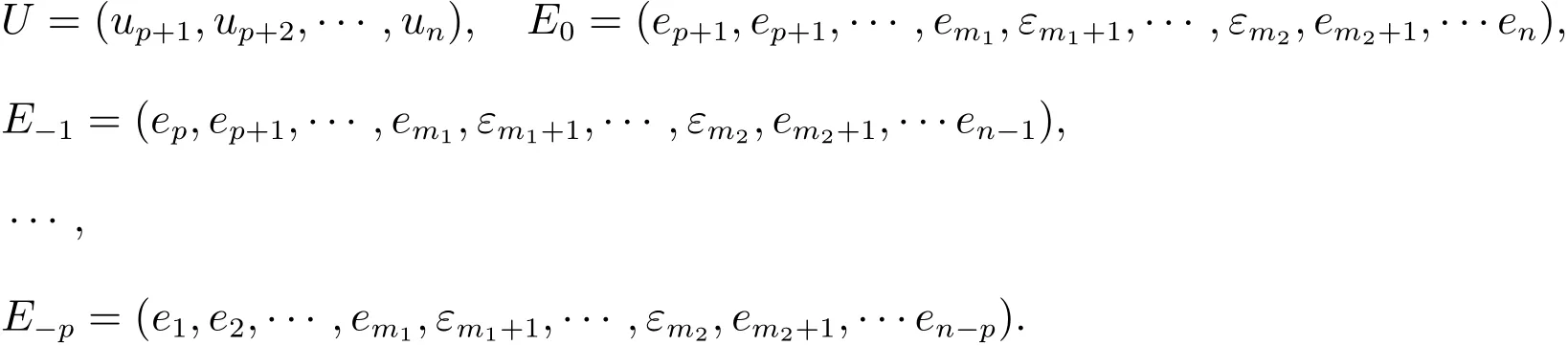
从而,公式(15)可以写成向量形式
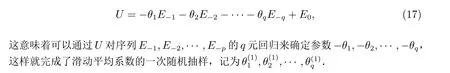

获取先验分布为IG(α,β)的参数的初始值
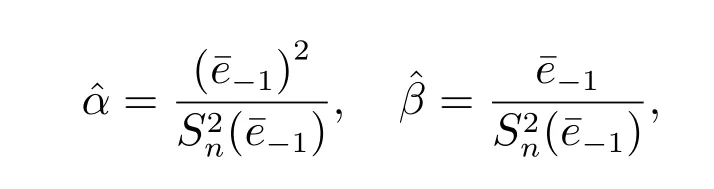
其中ei,-1= 1/e, i= 1,2,··· ,m1,m2,m2+ 1,··· ,n, εi,-1= 1/εi, i=m1,m1+1,··· ,m2.本节以零均值的ARMA(p,q)为例,给出基于M-H 抽样的潜变量MCMC 模拟算法的步骤:
步骤1 采用OLS 估计获取自回归系数、滑动平均系数以及随机误差项的初值
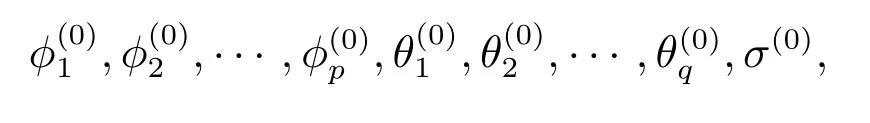
同时,获取一次随机误差项


5 触发式理财产品定价
在金融市场上存在许多理财产品,其中就包括触发式理财产品,例如见表1,其到期日的收益可以归结为如下公式

表1 挂钩于欧元兑美元汇率的触发式理财产品(起购金额:50000 元)
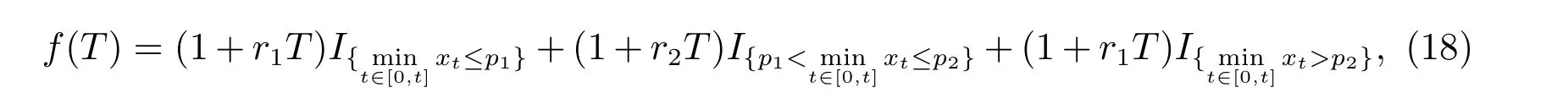
其中随机过程{xt,t ≥0}表示欧元兑美元的汇率,其随机结构见公式(1).
为了实现对理财产品进行价值分析,采用潜变量M-H 抽样方法获取汇率模型(1)的参数之后,对汇率的轨迹进行模拟.假定当前时刻为t时刻,理财产品在T时刻,将触发式理财产品剩余存续期(t,T]进行划分,即
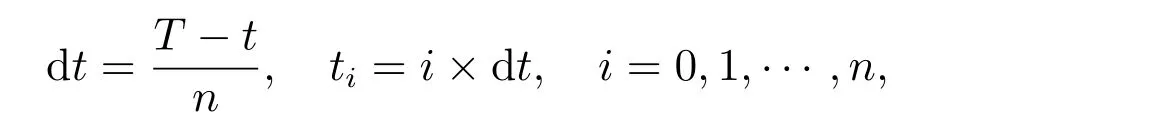
其中dt表示1 天,与图1 中的时间间隔相同,并假设汇率在理财产品存续期内的预测轨迹为
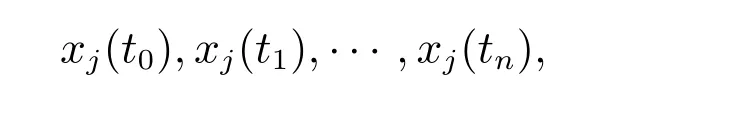
其中下标j表示{xj(ti), i= 1,2,··· ,n}对汇率的第j条轨迹模拟,从而触发式理财产品在到期日的第j次模拟结果表示为
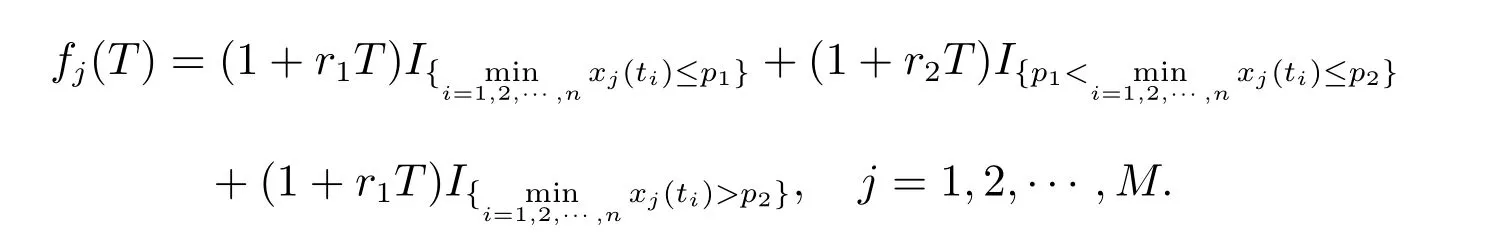
依据风险中性测度定价方法,收益为(18)的触发式理财产品在当前时刻t的价值满足
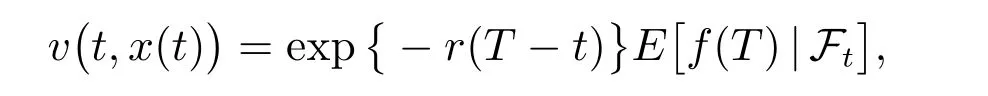
其中r表示银行的无风险利率,E[·|Ft]表示关于当前时刻σ-代数的条件期望.注意t0=t, tn=T,从而当M足够大时,采用矩估计方法可得触发式理财产品的一个估计
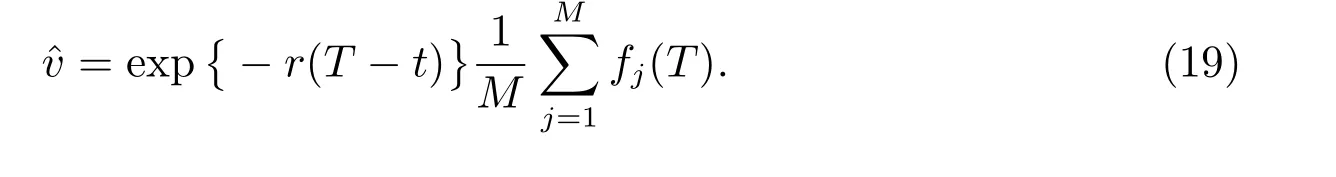
6 仿真分析
为了考察缺失序列MCMC 估计方法的有效性,本节考察ARMA 序列,将MCMC 方法和传统的OLS 方法进行比对分析.实验环境为Windows XP 系统,Intel(R)Core(TM)i7-6700K @4.00GHZ,内存16.0GB.本节的模拟计算采用编程软件R3.4.2.
6.1 数值比对
设定p=q= 1, φ1= 0.8, θ1= 0.5, σ= 0.1, m1= 100, m2= 150, n= 500,在样本数据实验中学者们常常采用Gibbs 抽样完成MCMC 模拟.遗憾的是,金融市场中的序列(例如汇率、股票以及指数的历史数据)往往存在异方差效应,Gibbs 抽样依据这些历史数据的后验分布进行采样,所获取的模拟序列也通常具备波动率聚集现象,这违背了Gibbs 抽样算法关于抽样序列的平稳性假设.为了说明这一问题,我们考察ARMA(1,1)序列,设置模型常数项c= 0,其R 语言模拟的AR(1)序列见图2.将模拟结果的中间去除视为缺失数据,其模拟结果见图3.
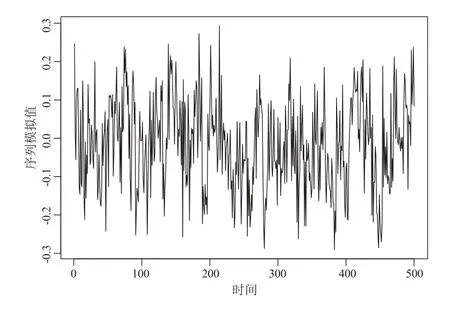
图2 ARMA(1,1)序列
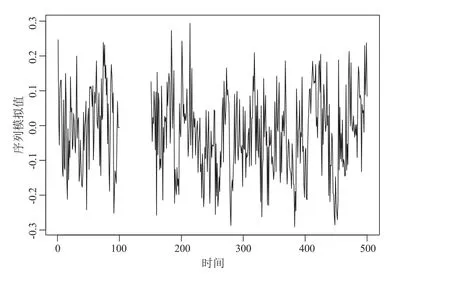
图3 数据缺失情形下ARMA(1,1)序列
考察传统的Gibbs 抽样方法.自回归系数φ1的Gibbs 抽样序列见图4,可以看出抽样序列出现了波动聚集现象.由于MCMC 法要求抽样序列平稳,这显然与MCMC 方法的基本原理不符.
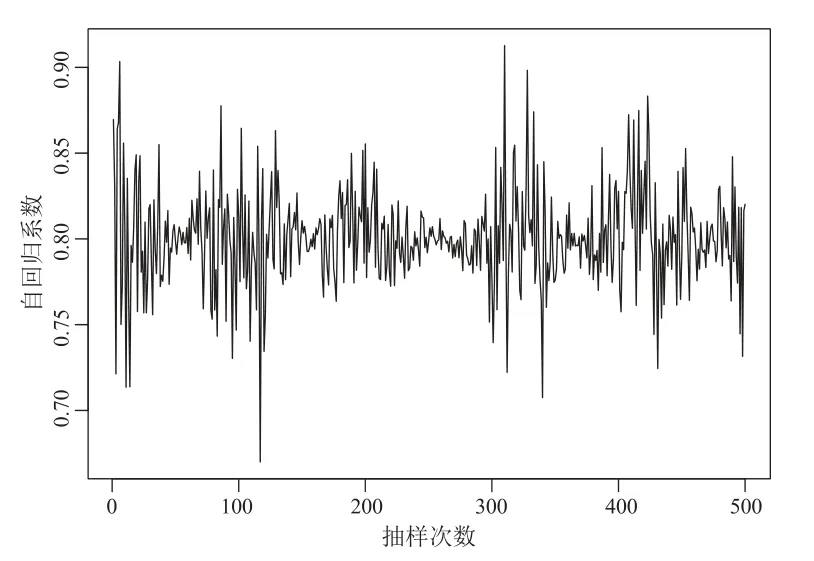
图4 自回归系数φ1 的Gibbs 抽样序列
接下来,考察基于潜变量M-H 抽样的MCMC 算法的模拟效果.注意由于传统的Gibbs 抽样在模拟ARMA 序列时产生了异方差效应,这不符合MCMC 算法的模拟条件,这里主要模拟潜变量M-H 方法的抽样参数序列是平稳的,这意味着针对ARMA 序列潜变量M-H 方法有更好的适应性.同时也比对模拟潜变量M-H 方法比传统的OLS 方法精度有所提高.
采用传统的OLS 方法、Gibbs 抽样方法以及M-H 抽样方法进行AR MA(1,1)序列的参数估计,结果见表2.在M-H 抽样运算中,首先对每个参数进行2500 次的预迭代消除初值对模拟结果的影响.从图5、图6 及图7 可以看出M-H 抽样获取的Markov 链趋于平稳,说明M-H 抽样估计的结果收敛.
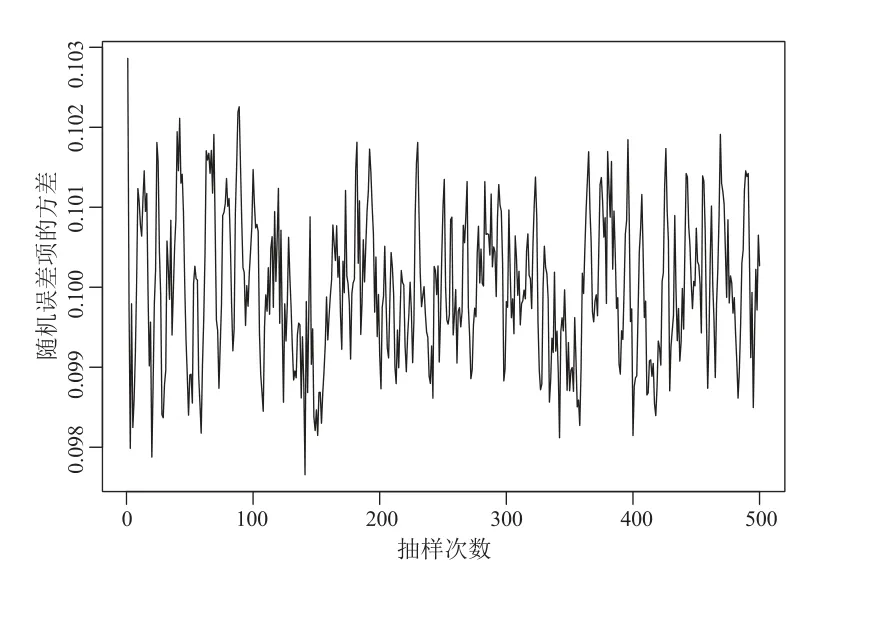
图7 σ 的M-H 抽样序列

图6 滑动平均系数θ1 的M-H 抽样序列
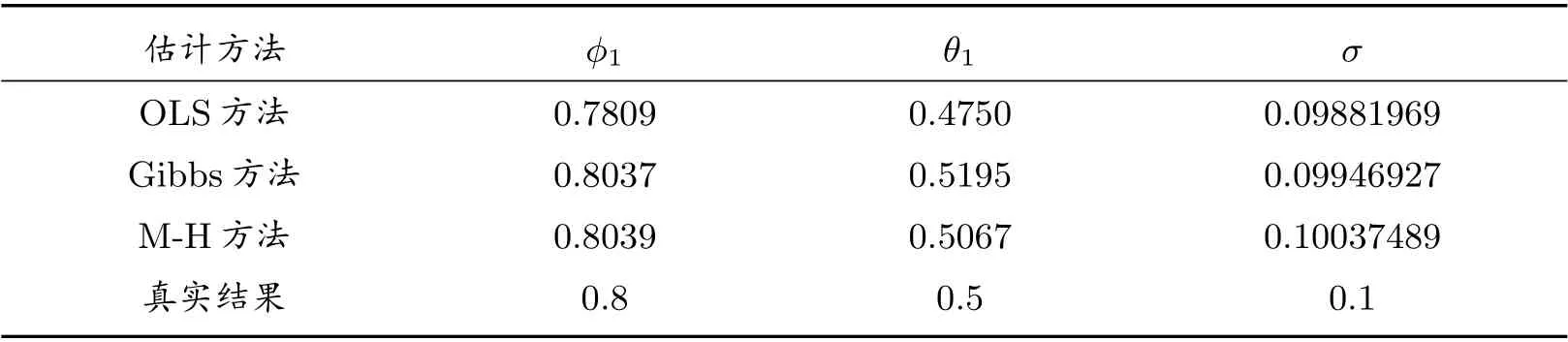
表2 模拟参数设定及估计效果
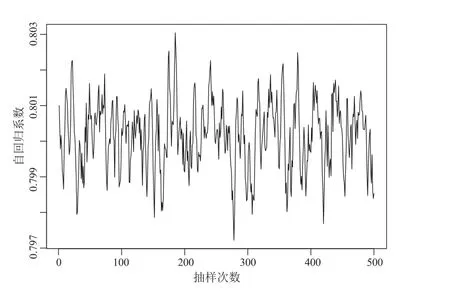
图5 自回归系数φ1 的M-H 抽样序列
之后再进行2500 次迭代,结果见表2,可以看出基于潜变量M-H 抽样的MCMC 方法有更好的模拟结果.连续模拟10000 个轮次,发现:
1) 就自回归系数φ1而言,潜变量M-H 抽样方法优于OLS 方法的次数为9903;
2) 就滑动平均系数θ1而言,潜变量M-H 抽样方法优于OLS 方法的次数为9647;
3) 就随机误差项的标准差σ而言,潜变量M-H 抽样方法优于OLS 方法的次数为9501.
在之后的部分,将利用MCMC 方法获取的汇率序列模型,研究触发式理财产品定价问题.
6.2 实证分析
本节将尝试分析表2 中触发式理财产品的价值,由于它们均挂钩于欧元兑美元的汇率,从而在新浪网财经板块收集了该汇率2018 年9 月20 日至9 月27 日的数据,时间间隔为4 小时,受开盘制度的影响周末的汇率出现了数据缺失,见图1.
根据Eacf 方法、AIC 准则和BIC 准则,确定汇率模型为AR(1),再依据M-H 抽样方法,模型的参数为
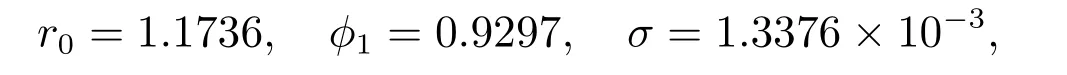
从而汇率模型(1)可以确定为
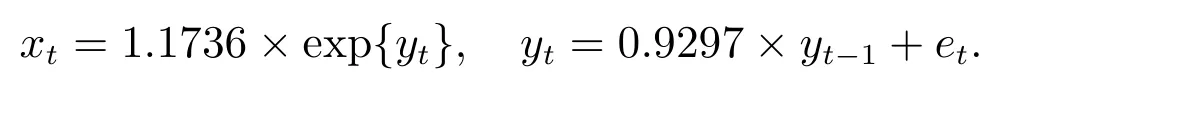
根据2018 年9 月20 日的银行利率信息,选取无风险利率r=0.0435, M=300000,并利用公式(19),获取三款来自农业银行的触发式理财产品的估计价格,其模拟价格情况见表1 最后一列.

