一类食饵具有Allee 效应的捕食-食饵模型的分歧解

曹 倩, 李艳玲

(1- 长安大学理学院，西安 710064; 2- 陕西师范大学数学与统计学院，西安 710119)

1 引言

Allee 效应指的是种群密度低时，种群单位增长率和种群密度之间正相关，该效应是当前反应扩散模型研究中的热点问题.近年来，许多实验表明物种存在双Allee 效应，例如，一种濒临灭绝的物种—岛屿灰狐，它们原产于美国加利福尼亚州海峡群岛的六个岛屿.金雕的捕食是幼年和成年岛屿灰狐的主要威胁.此外，它们在物种密度较低的情况下，雌性繁殖的可能性降低，这是由于雌性怀孕前缺乏配偶以及很难找到新的配偶.因此，岛屿灰狐的生长速度受到双Allee 效应的影响(繁殖困难带来的Allee 效应和捕食驱动的Allee 效应).在海洋生态系统中也存在双Allee 效应[1].然而，形成双Allee 效应的机制有很多，双Allee 效应对生物多样性保护很重要并且给系统带来复杂的动力学行为，因此研究双Allee 效应是十分必要的.本文研究如下食饵带有双Allee 效应的捕食-食饵模型

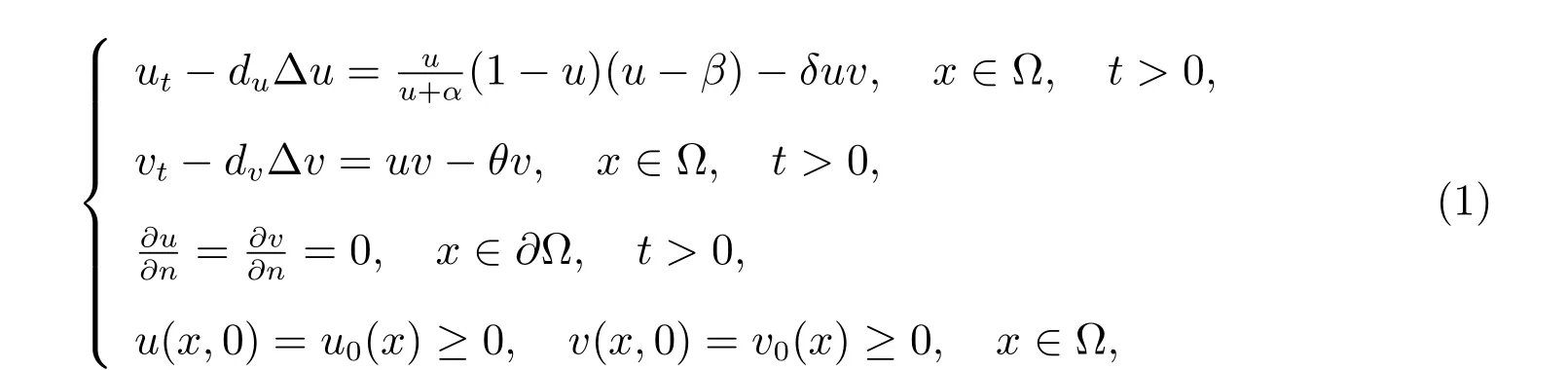
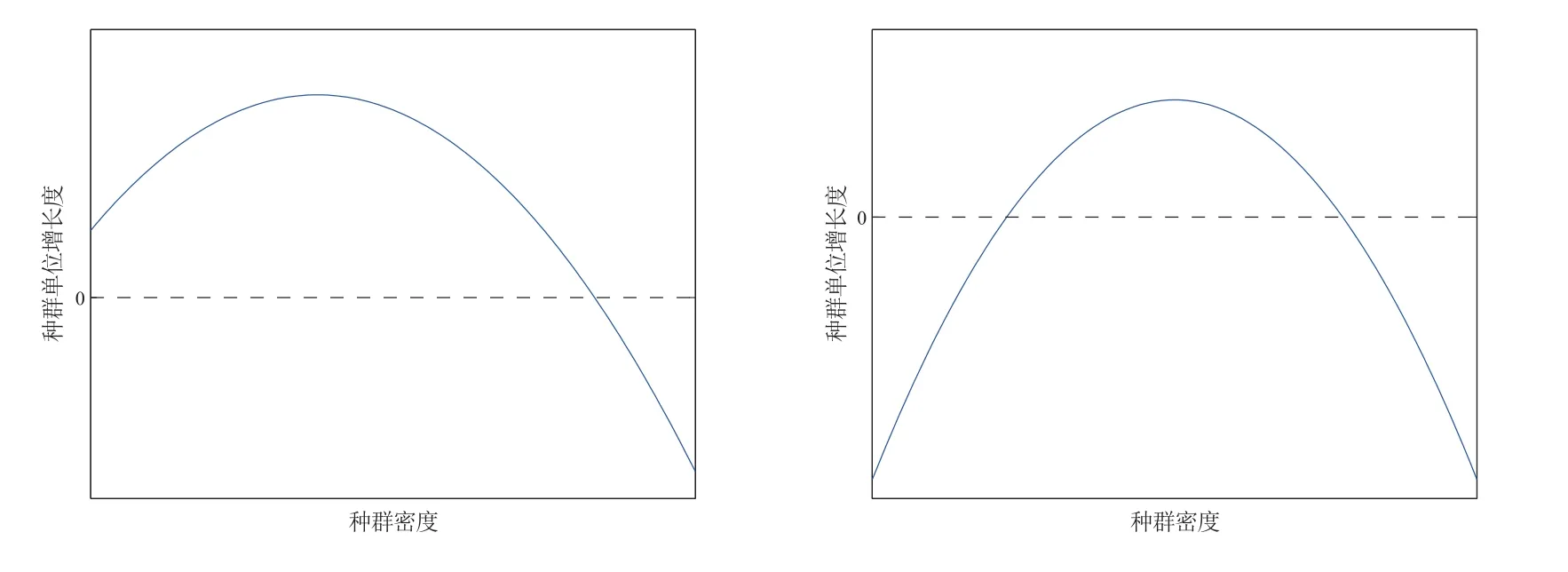
图1 弱Allee 效应和强Allee 效应定义的图示

近几十年来，很多学者已经对捕食-食饵型模型进行了广泛的研究[2–14]，其中文献[2]研究了在齐次Dirichlet 边界条件下一类具有强Allee 效应的捕食-食饵模型共存解的存在性.文献[3]研究了一类具有脉冲扰动的随机捕食-食饵系统的周期解和平稳分布.文献[4,5]分别研究了带有加法Allee 效应和乘法Allee 效应的捕食-食饵模型共存解的惟一性和多解性.然而在齐次Neumann 边界条件下带有双Allee 效应的扩散捕食-食饵模型的研究很少见.因此，本文主要研究系统(1)所对应平衡态系统的分歧解的存在性.下面考虑系统(1)相应的平衡态系统

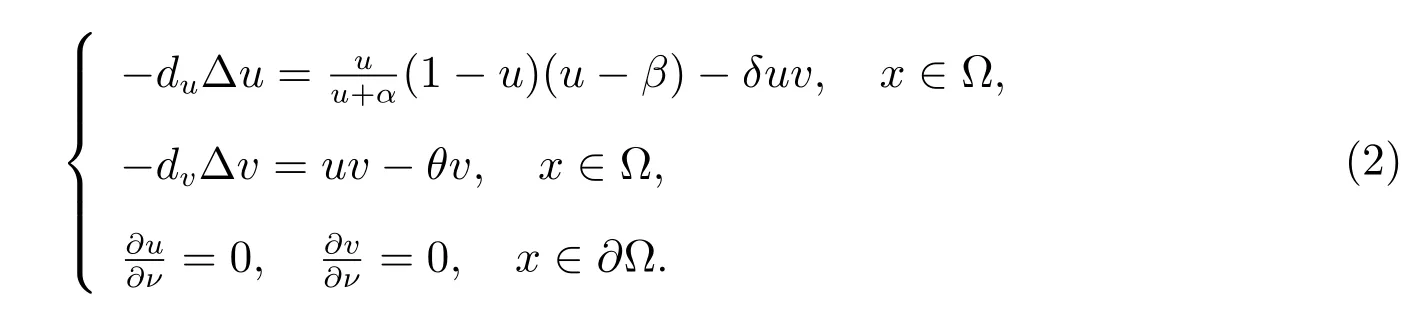
2 稳定性分析

本节利用稳定性理论分别研究强Allee 效应和弱Allee 效应情形下系统(2)常数解的稳定性.这对后面分歧解的研究有着重要作用.

首先，我们研究强Allee 效应(0＜β ＜1)的情形.此时，系统(2)有四个常数解：平凡解(0,0)，半平凡解(1,0)和(β,0)，唯一的正常数解(θ,vθ)，其中

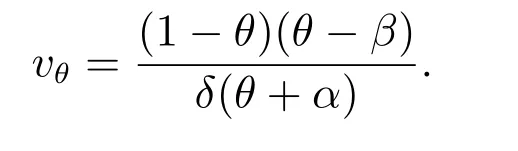
当且仅当β ＜θ ＜1 时，正常数解(θ,vθ)存在.

为了记号简单，我们记u=(u,v)和

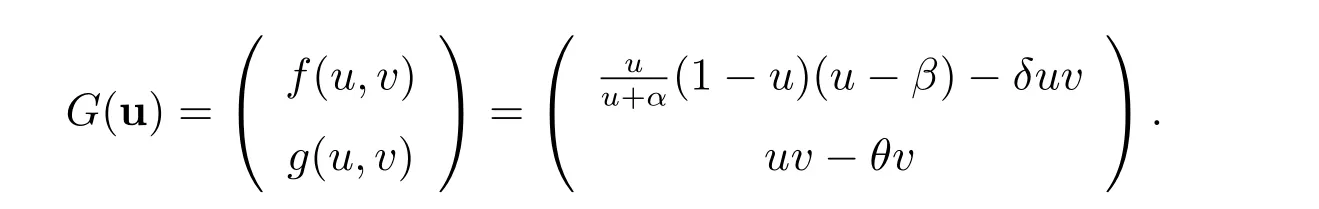
下面我们得到G(u)在u*=(u*,v*)处的线性化

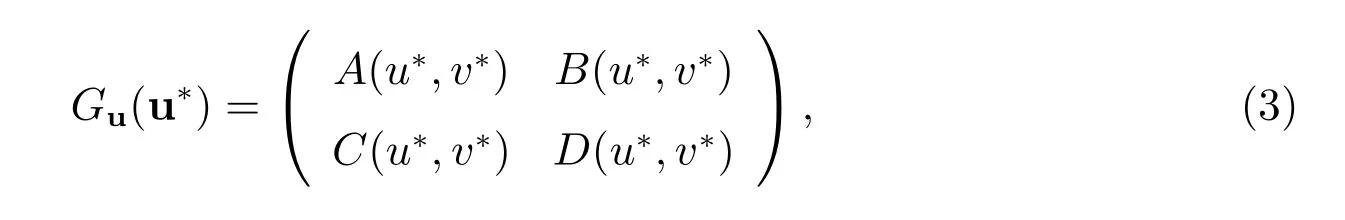
其中

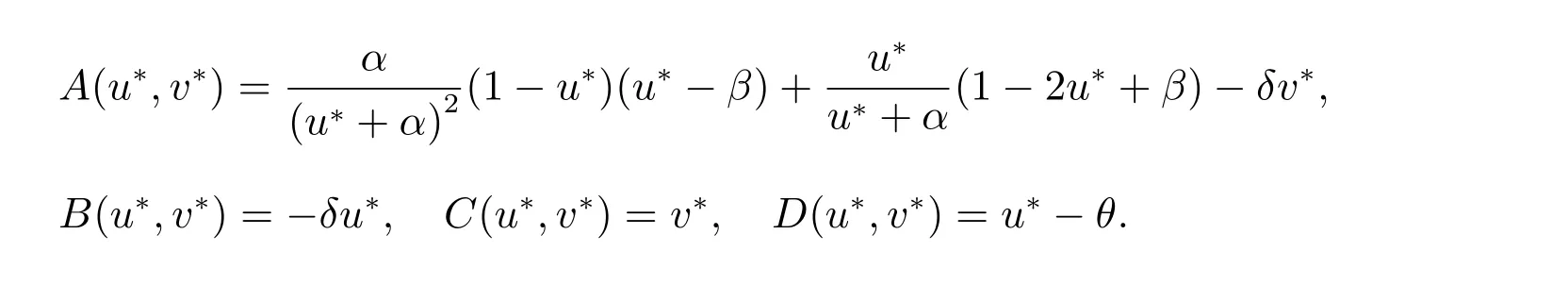
假设{λn}是-Δ 在齐次Neumann 边界条件下的一列可列特征值，满足0 =λ0＜λ1＜λ2＜··· ＜λj ＜···.设mj是λj(j= 0,1,2,···)的代数重数并且φjk(1≤k ≤mj)为λj对应的标准化特征函数.下面定义

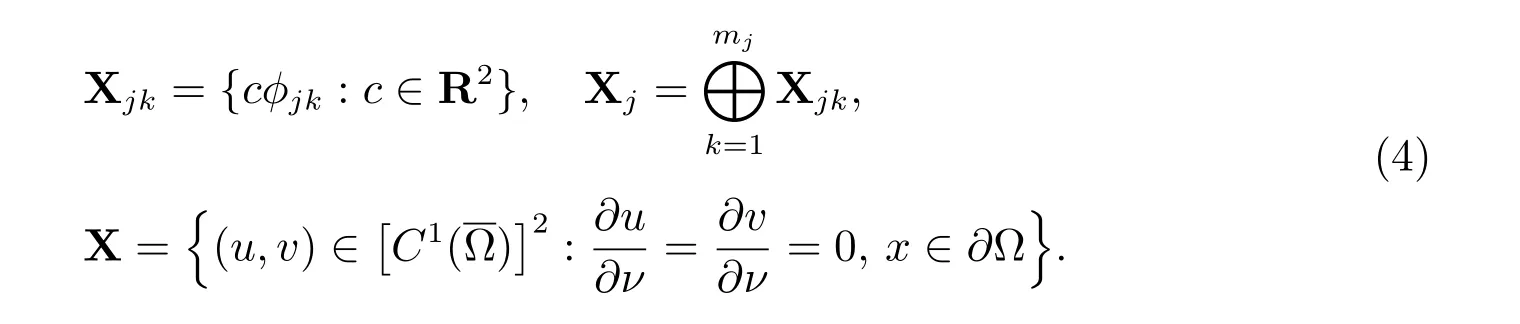
容易得到

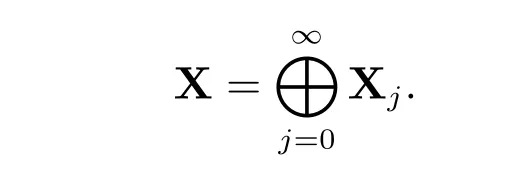
下面将系统(2)在u*处线性化

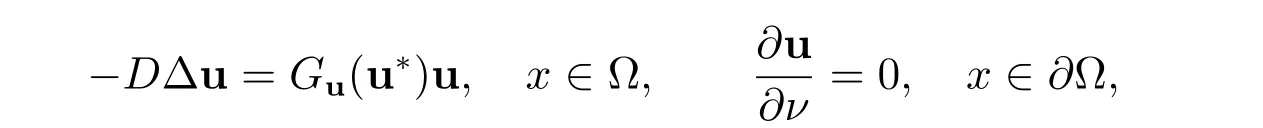
其中

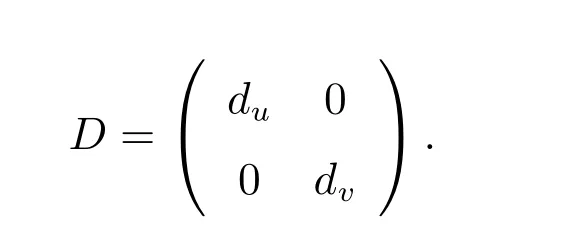
下面记

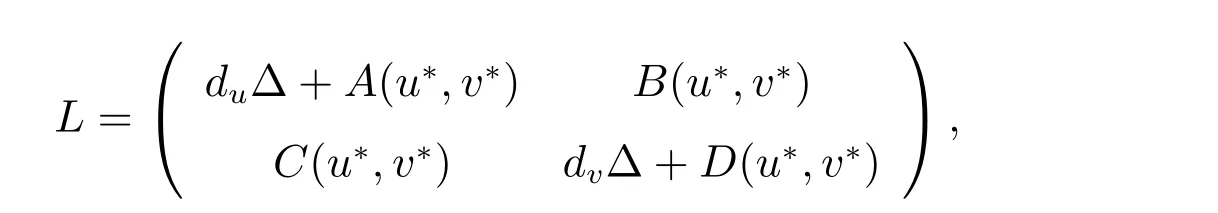
其中A(u*,v*), B(u*,v*), C(u*,v*)和D(u*,v*)如上所述.

假设(Φ(x),Ψ(x))是L算子相应于特征值μ的特征函数.那么有

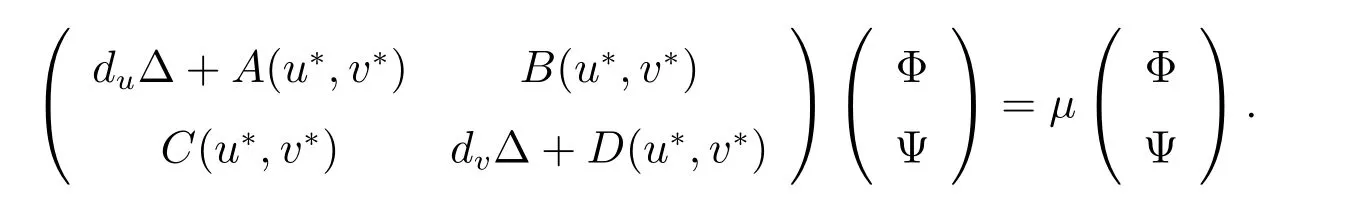
令

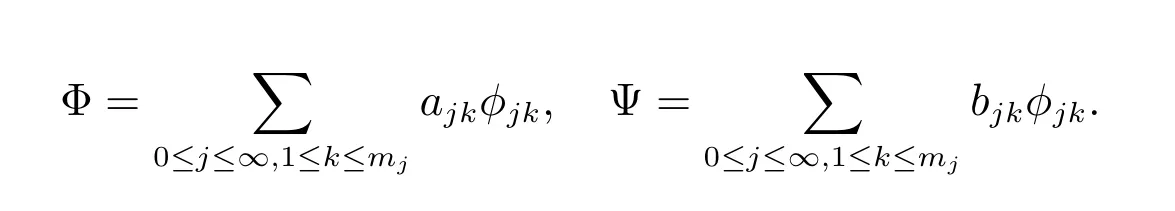
则可得到

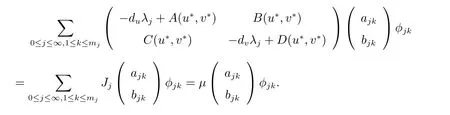
因此，我们知道当且仅当存在某个j ≥0，使得矩阵μI-Jj的行列式等于0，即

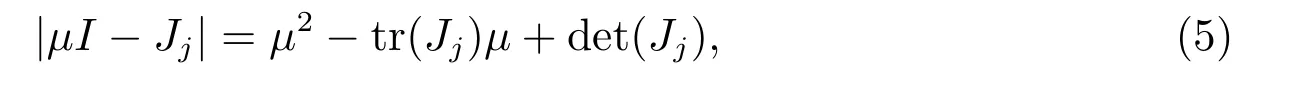
其中

因此，类似于文献[15]，我们有以下结论：

(i)

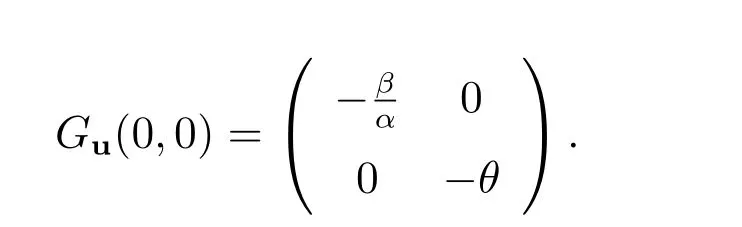
显而易见，(0,0)局部渐近稳定.

(ii)

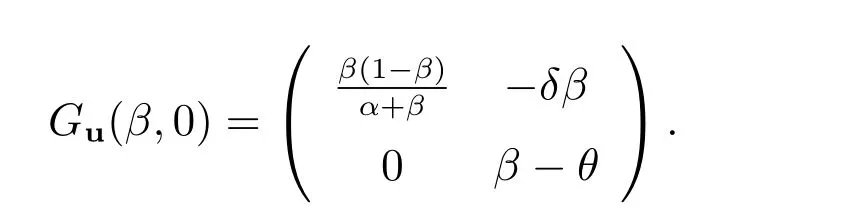
显而易见，(β,0)不稳定.

(iii)

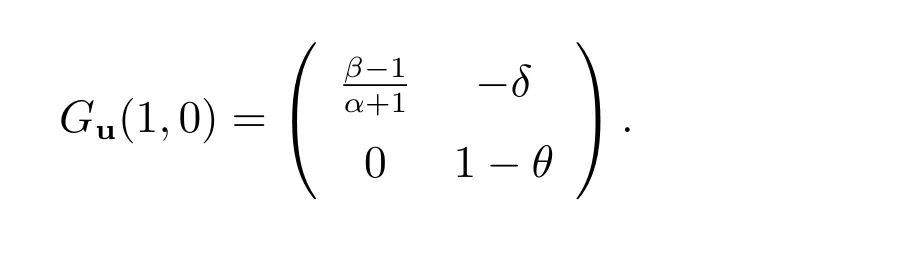
当θ ＞1 时，我们得到tr(Ji)＜0 和det(Ji)＞0(i ≥0).因此，(1,0)局部渐近稳定；

当0＜θ ＜1 时，我们得到

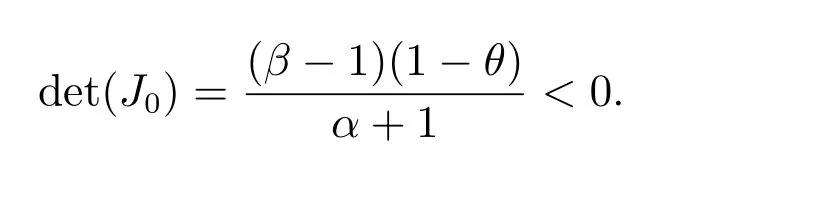
所以(1,0)不稳定.

(iv)

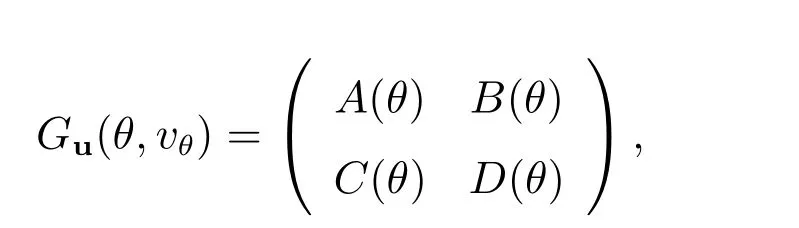
其中

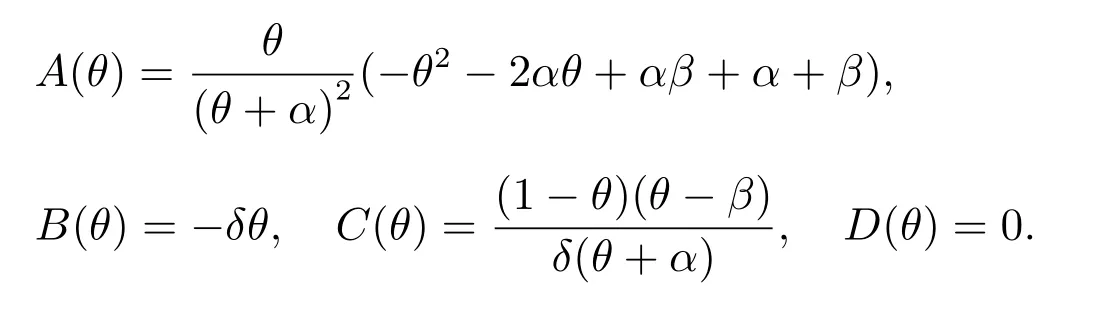
令

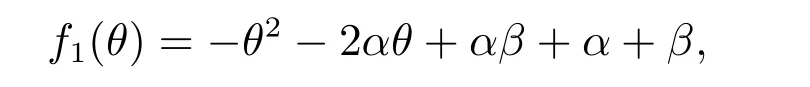
那么A(θ) = 0 等价于f1(θ) = 0.由f1(θ)的表达式知，当θ ∈(-α,+∞)时，f1(θ)单调递减，所以f1(θ)在θ ∈(β,1)⊂(-α,+∞)时单调递减.此外

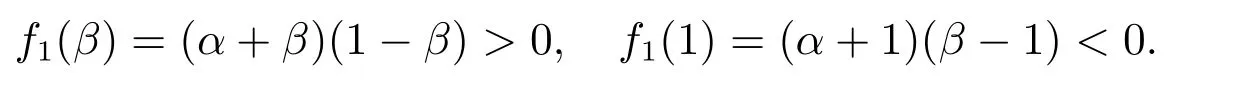
那么存在唯一的

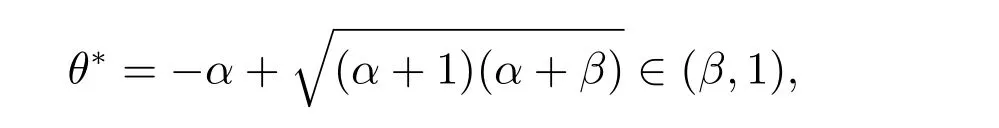
使得

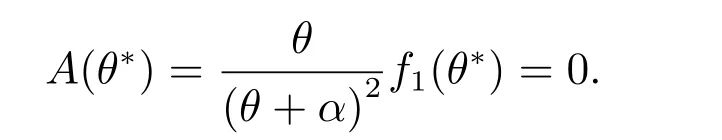
(a) 当β ＜θ*＜θ ＜1 时，我们得到tr(Ji)＜0 和det(Ji)＞0(i ≥0).因此(θ,vθ)局部渐近稳定.

(b) 当β ＜θ ＜θ*＜1 时，我们得到A(θ)＞0.对于i=0，我们有tr(J0)＞0，这说明(5)至少有一个有正实部的根.因此(θ,vθ)不稳定.

综上可得下面的定理，给出强Allee 效应(0＜β ＜1)情形下常数平衡解(0,0),(β,0),(1,0)和(θ,vθ)的稳定性.

定理1 假设du, dv, α, δ ＞0,0＜β ＜1.那么有下列结论：

(i) 当θ ＞0 时，(0,0)局部渐近稳定；

(ii) 当θ ＞0 时，(β,0)不稳定；

(iii) 当θ ＞1 时，(1,0)局部渐近稳定；当0＜θ ＜1 时，(1,0)不稳定；

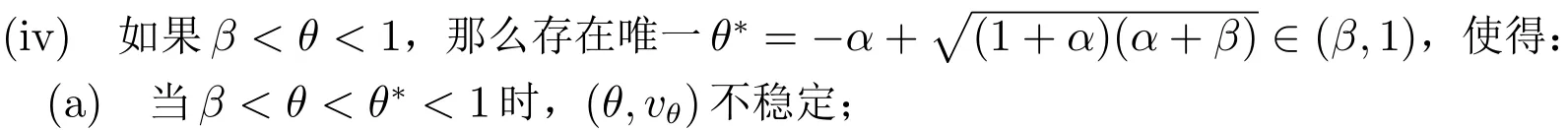
(b) 当β ＜θ*＜θ ＜1 时，(θ,vθ)局部渐近稳定.

接下来，我们考虑弱Allee 效应(-1＜β ＜0)的情形，此时系统(2)有平凡解(0,0)，半平凡解(1,0)和唯一正常数解(θ,vθ)，其中当且仅当0＜λ ＜1 时，(θ,vθ)存在.下面我们研究这些常数解的稳定性，下述稳定性定理证明与定理1 类似，此处定理证明省略.

定理2 假设du, dv, α, δ ＞0,-1＜β ＜0.那么下述结论成立：

(i) 当θ ＞0 时，(0,0)不稳定；

(ii) 当0＜θ ＜1 时，(1,0)不稳定；当θ ＞1 时，(1,0)局部渐近稳定；

(iii) 如果

那么(θ,vθ)局部渐近稳定.

3 分歧解的存在性

这一节，我们分别对强Allee 效应(0＜β ＜1)和弱Allee 效应(-1＜β ＜0)的分歧解进行分析.我们以du为分歧参数，并利用局部分歧理论研究正常数解(θ,vθ)邻域上局部分歧解的结构和性质.当研究Ω=(0,l)时，系统(2)对应的如下椭圆系统

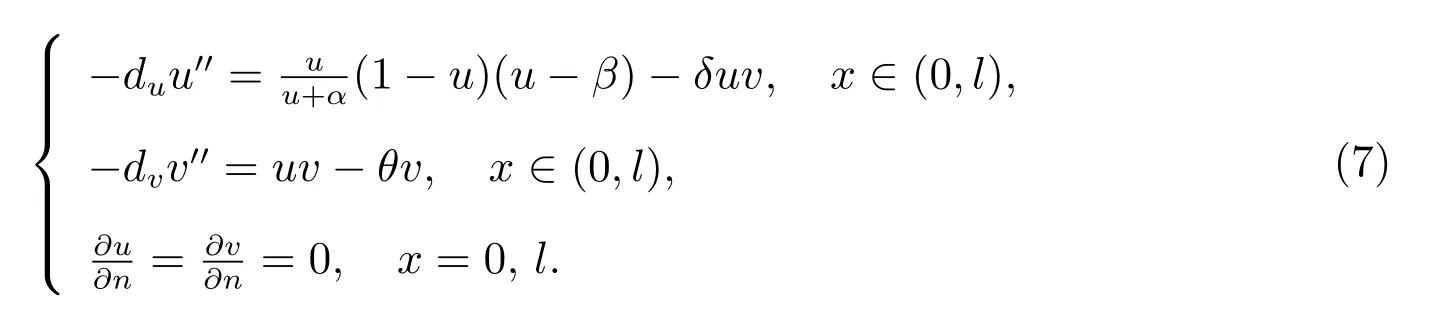
下面，我们考虑特征值问题

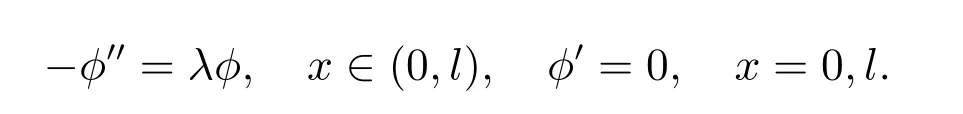
这个特征值问题有一系列简单特征值

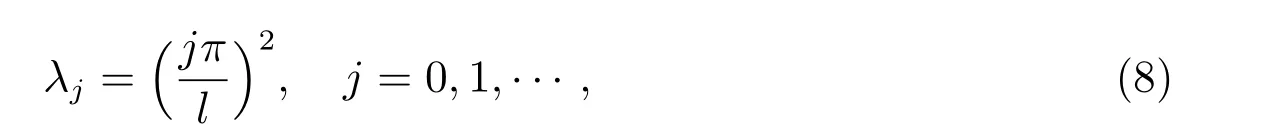
和相应标准化特征函数

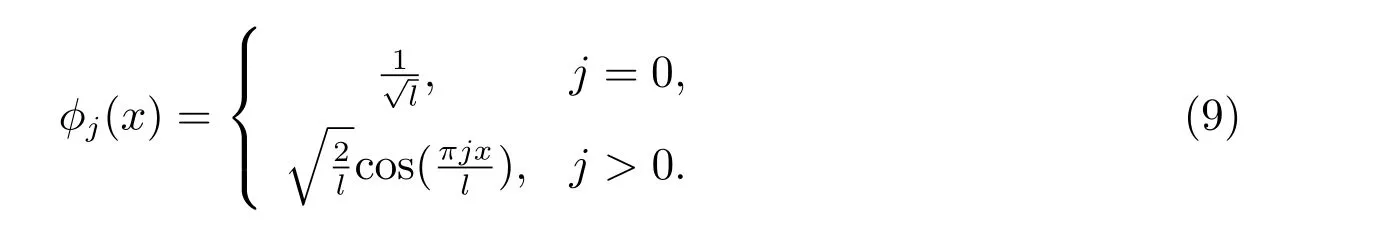
显然，这些特征函数构成L2(0,l)上一组正交基.

并把S看做具有C2(Ω)范数的Banach 空间.易知系统(7)的解是映射ˆF: (0,∞)×S →Y的零点，所以

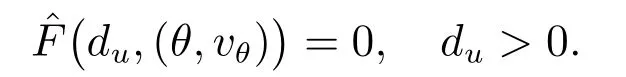
对某个τ ＞0，如果ˆF(τ,(θ,vθ))在(0,∞)×S上的邻域包含不同于(du,(θ,vθ))(du ＞0)的零点，那么(τ,(θ,vθ))为方程ˆF= 0 的分歧点.根据文献[16]的定理1.7，如果下述条件成立，则(τ,(θ,vθ))为方程ˆF=0 的分歧点.

综上，我们得到下述强Allee 效应(0＜β ＜1)情形下的局部分歧结论.

定理3 假设

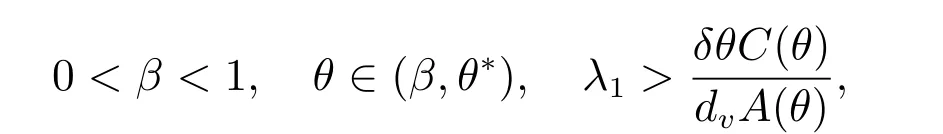
和当k/=j时，dj/=dk，那么(dj,(θ,vθ))是ˆF= 0 的一个分歧点.并且，当|s|足够小时，系统(2)有一个单参数的非常数解Γj(s)=(du(s),u(s),v(s))，其中和du(0)=dj.此外，du(s), u(s), v(s)是关于s连续可微的函数.

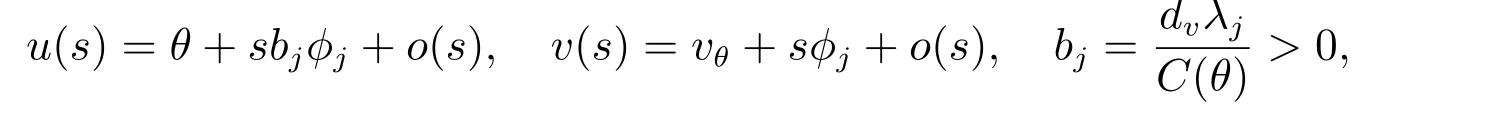
证明 考虑ˆF(du,u)关于u 在正常数解(θ,vθ)处的Fr´echet 导数及ˆFu(du,(θ,vθ))的伴随算子

其中

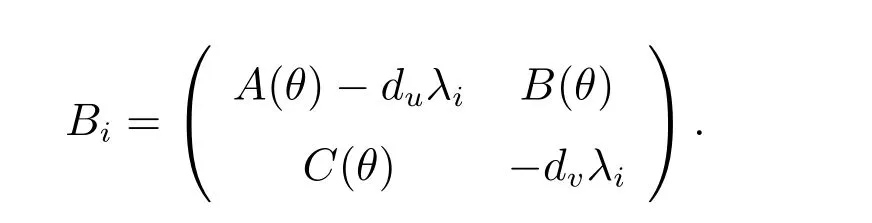
由此可得

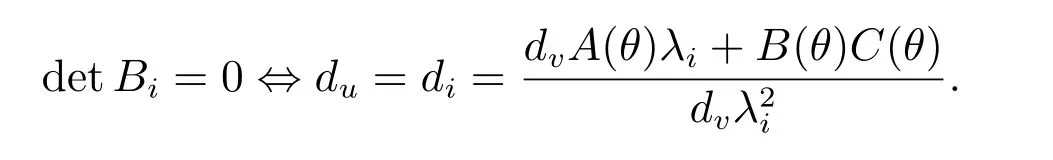
取du=dj，则有

所以，我们得到

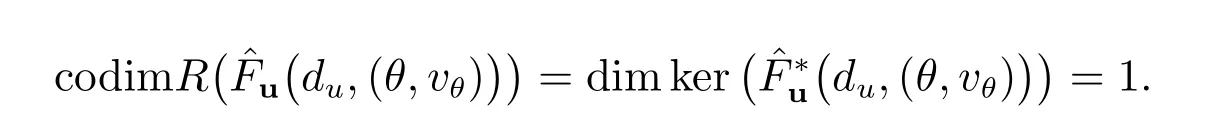
因此条件(b)成立.

最后，因为

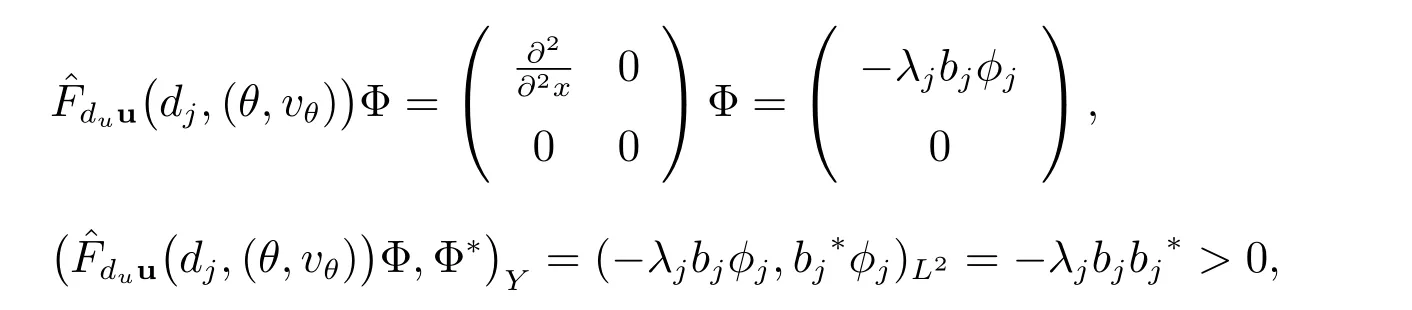
我们得到

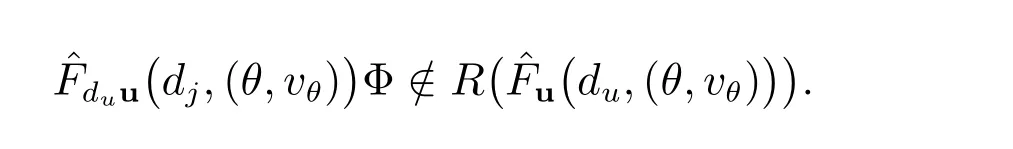
所以条件(c)成立.

类似于定理3 的证明方法，我们可以证明弱Allee 效应(-1＜β ＜0)情形下的局部分歧结论.此处证明过程省略.

定理4 假设

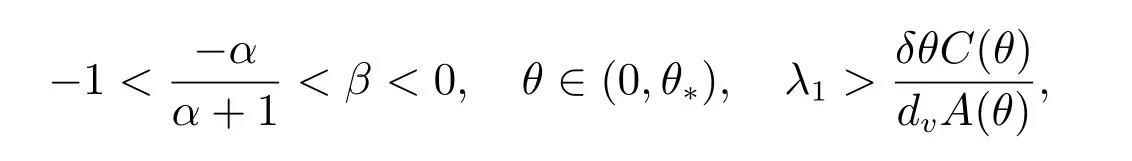
和当k/=j时，dj/=dk，那么(dj,(θ,vθ))是ˆF= 0 的一个分歧点.并且，当|s|足够小时，系统(2)有一个单参数的非常数解Γj(s)=(du(s),u(s),v(s))，其中

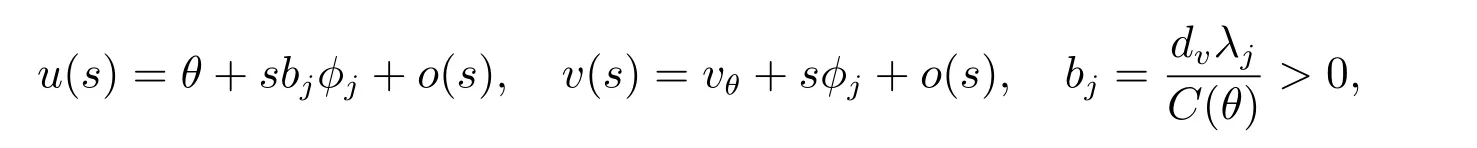
和du(0)=dj.此外，du(s), u(s), v(s)是关于s连续可微的函数.

4 数值模拟

本节利用Matlab 软件进行数值模拟，用以验证前面的理论分析.这里研究强Allee 效应(0＜β ＜1)的情况.弱Allee 效应情形可以用类似的方法研究.

图2 中的参数选取α=1, β=0.2, δ=3, θ=0.4, l=3, t=2000，此时

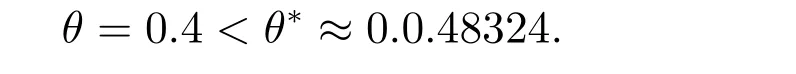
图3 中的参数选取α=1, β=0.2, δ=3, θ=0.8, l=3, t=2000.此时

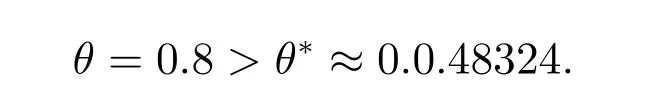
图2 和图3 验证了定理1 和定理3：强Allee 情形下，存在一个临界值θ*，使得当θ ∈(θ*,1)时，(θ,vθ)局部渐近稳定；而当θ ∈(β,θ*)时，(θ,vθ)不稳定，此时系统(2)至少存在一个非常数正解.

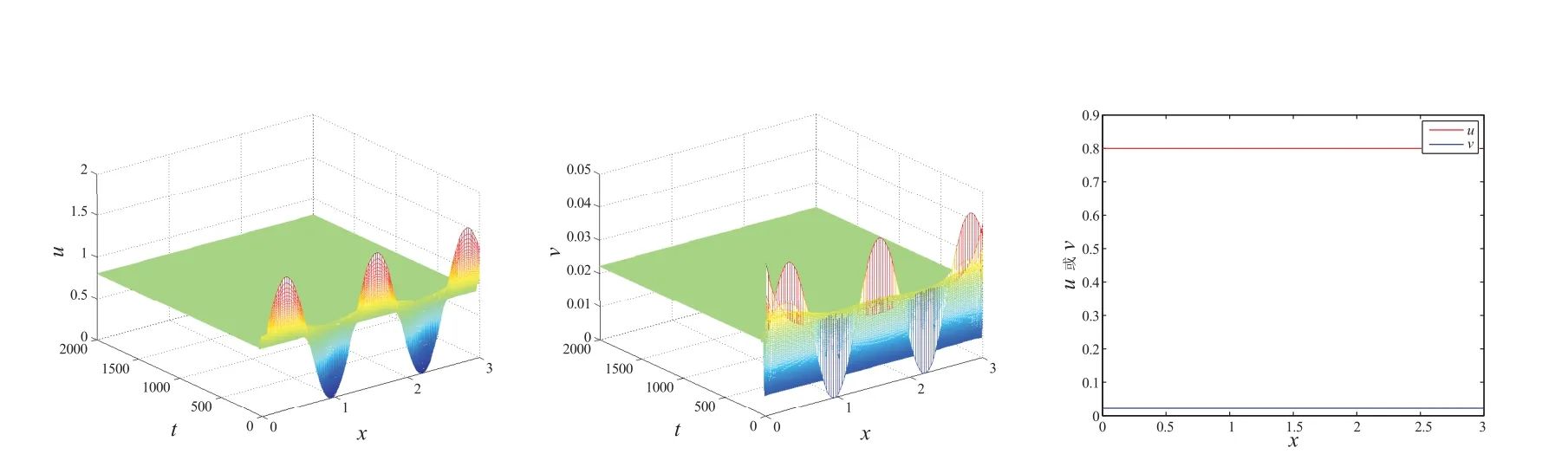
图3 λ ＞λ*时，系统(1)共存解(u,v)的时空图和系统(1)在t=2000 时，共存解(u,v)的空间分布

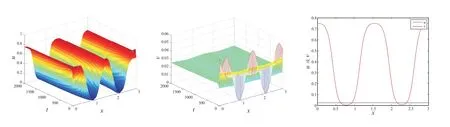
图2 λ ＜λ*时，系统(1)共存解(u,v)的时空图和系统(1)在t=2000 时，共存解(u,v)的空间分布

5 结语

本文主要运用稳定性理论和局部分歧理论研究了一类食饵具有双Allee 效应的捕食-食饵模型，得到了该模型常数解的稳定性、分歧解的存在性和分歧解的性质.结果表明，当

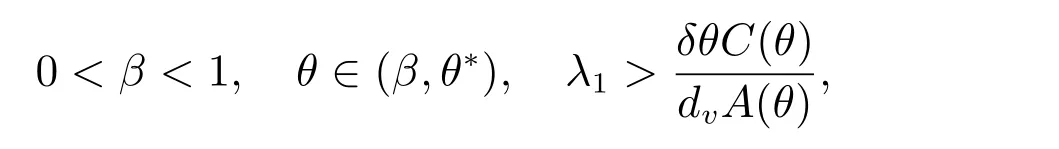
和当k/=j时，dj/=dk，那么(dj,(θ,vθ))是ˆF=0 的一个分歧点；当

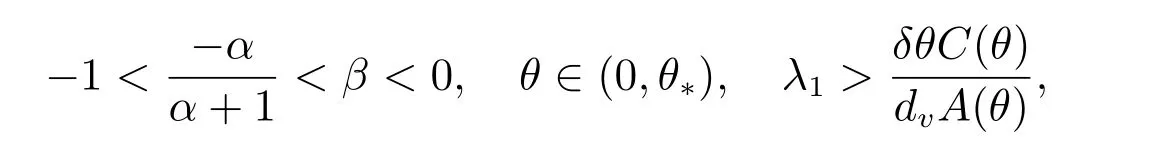
和当k/=j时，dj/=dk，那么(dj,(θ,vθ))是ˆF=0 的一个分歧点.