试验室条件下304SS冲击式涡轮叶片疲劳寿命研究
刘士杰 刘恒 刘继超 梁国柱 张军伟 王慧
试验室条件下304SS冲击式涡轮叶片疲劳寿命研究
刘士杰1刘恒1刘继超2梁国柱3张军伟4王慧1
(1 北京航天动力研究所低温液体推进技术实验室,北京 100076;2 北京机床研究所有限公司,北京 100102;3 北京航空航天大学宇航学院,北京 102206;4 北京航天发射技术研究所,北京 100076)
可重复使用液体火箭发动机对冲击式涡轮叶片疲劳寿命的验证需求越来越强烈,然而,目前叶片疲劳试验以成本高昂的搭载试车为主,且冲击式涡轮叶片尺寸小,试验难度大。为此,本文以某型液体火箭发动机涡轮一级动叶为研究对象,建立了小尺寸液体火箭发动机涡轮叶片疲劳寿命仿真与试验室考核方法,从理论和试验的角度对叶片疲劳寿命实验室考核试验的可行性和合理性进行了论证。本文的研究可以为液体火箭发动机涡轮叶片和其他部件疲劳寿命的评估提供参考。
冲击式涡轮叶片;疲劳试样;电火花加工;可重复使用性;试验验证
0 引言
可重复使用航天运载器是未来航天发展的方向之一,因此,可重复使用液体火箭发动机的研究具有重要的应用价值。涡轮叶片作为液体火箭发动机的关键部件,其疲劳寿命的理论与试验研究对确定发动机的可重复使用性尤为重要。
国内外学者以航天飞机主发动机(Space Shuttle motor Engine,SSME)高压液氢涡轮泵(High-Pressure Fuel Turbopump,HPFTP)为对象,开展了大量的针对涡轮叶片疲劳寿命的相关研究。Cikanek[1]指出,从1978年至1987年,SSMEHPFTP共发生6次故障,其中3次是由涡轮叶片破坏引起的。涡轮叶片故障导致整个涡轮泵彻底破坏,大块碎片飞散,严重毁坏发动机的其他结构件。为提高HPFTP的重复使用能力,1988年,Abdul-Aziz[2]对定向凝固合金MAR-M246和单晶高温合金PWA-1480涡轮叶片材料的非线性热—固耦合问题进行了研究,结果表明两种材料均具有几百次低周热疲劳的承受能力。1996年,Abdul-Aziz[3]又研究了HPFTP第一级涡轮叶片启动、关机、稳态工作阶段的非弹性变形行为,以及疲劳裂纹的扩展问题,指出热应力大约占到总应力的20%,涡轮叶片高应力区发生在第四榫齿处,工作循环使得这些薄弱部位率先出现疲劳损伤。由于涡轮叶片材料力学行为的复杂性和热机械载荷复杂性的影响,开展涡轮叶片热机械疲劳的理论与试验研究,弄清影响涡轮叶片循环寿命的主要因素,对涡轮叶片的可重复使用性的设计分析很有必要。2012年,郁大照[4]等利用有限元方法对燃气涡轮静强度进行了计算分析,得到了温度与转速耦合作用下的变形与应力分布,有效地证明了叶片与轮盘具有足够的强度裕度。2013年,石多奇等[5]利用修正的Chaboche本构模型和Kachanov损伤模型对定向凝固单晶镍基合金的各向异性进行了试验和有限元分析,研究成果对单晶镍基合金的各向异性拉伸特性和蠕变行为的研究有借鉴意义。2013年,王荣桥[6]通过在叶尖部位铸造夹持叶冠,开展了单晶涡轮叶片热机械疲劳的试验研究,对于尺寸较大的单个叶片来说,该设计的最大特点是方便快捷。航天冲击式涡轮叶片一般尺寸较小,且与轮盘采用整体式铸造或铣削加工,叶片试样的制备困难,这使得实验室条件下开展这类叶片的疲劳寿命试验比较困难。为了解决这个问题,2021年,刘士杰等[7]利用电火花加工方法制备了小尺度冲击式航天涡轮叶片疲劳试样,并对叶片试样的几何形貌、表面微结构、叶片受力状态进行了分析。结果表明,制备的叶片试样与实际叶片在整体和局部细节尺寸上一致性较好,满足试验要求。与航空领域相比,我国在航天涡轮叶片疲劳寿命上的研究还不多。十二五、十三五期间,北京航天动力研究所联合北京航空航天大学宇航学院开展了液体火箭发动机可重复使用性的研究,本文在叶片试样制备和材料力学行为研究的基础上,继续以某型液体火箭发动机涡轮一级动叶为对象,对试验室条件下304SS涡轮叶片的疲劳寿命仿真和试验验证方法进行了研究。
1 计算模型
1.1 物理模型
某型液体火箭发动机涡轮动叶是整体加工成形的小尺寸冲击式涡轮叶片,如图1所示。要在试验室条件下开展这类叶片的疲劳试验难度较大,这主要是因为:1)利用切割单个叶片的方法制备疲劳试样会损伤轮盘和围带附近的叶身形貌,造成叶片试样的初始缺陷;2)切割的单个叶片夹持困难,不易开展疲劳试验;3)叶片尺寸小,若仿照航空叶片疲劳试样制备方法,利用焊接方法制备疲劳试样会损伤叶片的主体结构。
鉴于以上原因,应在试验室条件下开展简化叶片(即试样)的疲劳寿命研究,简化原则如下:1)应保证试验段(对应叶身)的几何尺寸与真实叶片叶身一致,以确保二者宏观上具有相同的基本力学性能;2)应保证试样与真实叶片的加工工艺一致,以确保二者加工表面上基本的微观力学特性相同;3)应保证叶片和试样的局部细节(如倒角大小)质量一致,以确保影响二者疲劳寿命的关键因素相同,避免试验结果表现出较大的寿命分散性。
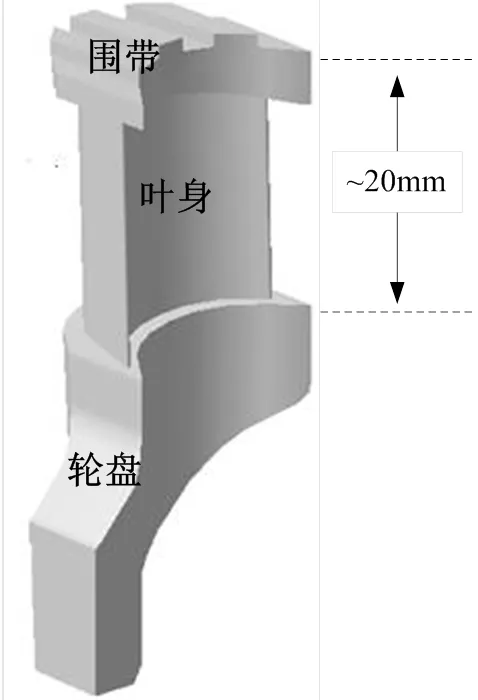
图1 某型液体火箭发动机涡轮叶片模型
本文采用电火花加工方法制备疲劳试样,相关加工参数与结果见文中表格。液体火箭发动机采用膨胀循环后,涡轮入口燃气温度接近常温,为此,本文开展了离心负荷下叶片疲劳寿命的仿真与试验研究。
1.2 疲劳寿命模型
本文利用低周疲劳寿命模型研究叶片寿命。低周疲劳寿命是通过总应变幅、塑性应变幅和弹性应变幅的关系得来的,即Basquin–Manson –Coffin方程
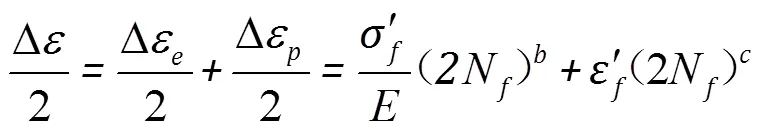
式中,2N表示疲劳试验中应力应变曲线总的反转次数。公式(1)适用于完全对称循环载荷的情形。然而,大多数结构件的工作过程中是存在平均应力与平均应变的,比如航空涡轮叶片在“0—起飞—0”和“0—最大续航—0”的飞行状态下存在平均拉应力。为了在疲劳寿命中考虑平均应力m和平均应变m的影响,Smith、Watson和Topper提出如公式(2)所示的寿命模型


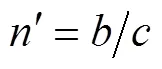

利用公式(6)所示的Pälmgren–Miner线性累计损伤法则计算叶片工作过程中的疲劳损伤

1.3 材料力学本构模型
刘士杰等[9]利用Chaboche混合硬化弹塑性本构模型对304SS的材料力学行为进行了研究,为了获得本文研究条件下叶片的力学状态,选取如表1所示的Chaboche随动硬化模型参数。
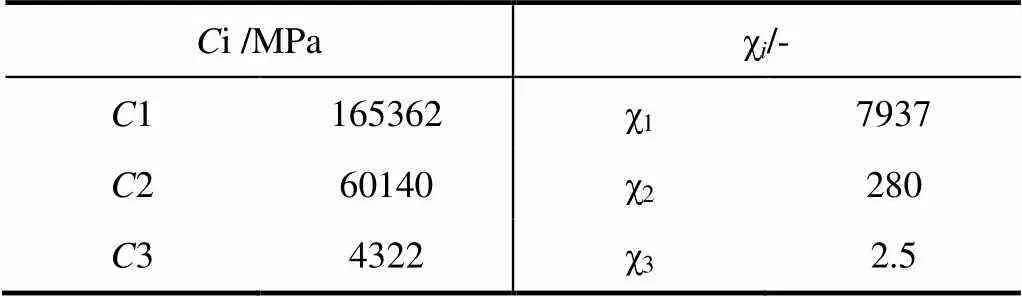
表1 304SS Chaboche随动硬化参数[9]
2 疲劳寿命的仿真与试验
2.1 疲劳试验
为了获取材料疲劳寿命模型参数,本文采用文献[10]中的圆棒疲劳试样,参照美国材料测试协会(ASTM-American Society for Testing and Materials)的规范[11]要求,利用SDS100电液伺服低周疲劳试验机(图2)进行材料疲劳寿命试验。试验中,利用常温引伸计(图3)实现应变的控制和测量。

图2 SDS100电液伺服疲劳试验机
低周疲劳试验的失效判据是:当试件出现明显可见的疲劳裂纹或迟滞回线上拉伸与压缩弹性模量的比值变化到大于等于0.5,认为试棒疲劳失效。表2是试验获取的低周疲劳寿命数据,图4是与表2对应的低周疲劳试验中试样的损伤情况。试样的损伤部位都发生在试样中段位置,这样的结果符合试验规范要求,即从试验效果上来说,所得试验结果是有效的。

图3 常温引伸计
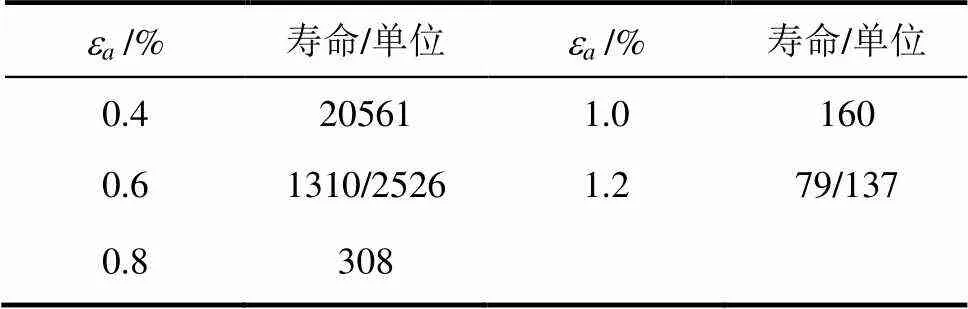
表2 低周疲劳试验数据

图4 试样损伤情况
2.2 疲劳寿命仿真
2.2.1 疲劳寿命模型参数识别
利用弹性应变幅—寿命关系和塑性应变幅—寿命关系,分别对表2所示的试验数据做线性回归分析以获取疲劳寿命模型的参数值。回归分析中的相关系数由公式(7)计算。


表3 304SS低周疲劳寿命参数
图5给出了试验结果以及根据试验结果分析得到的回归曲线。弹性应变—寿命回归曲线和塑性应变—寿命回归曲线的相关系数分别是0.508和0.908。由于试验过程中的影响因素很多,可能会有异常数据掺杂在试验数据当中,所以对试验结果做了进一步的异常数据分析。图6给出了数据残差,图中小圆圈代表数据残差值,过残差值的线条表示置信区间下的误差带,经过观察分析发现2号数据异常。
弹性应变—寿命曲线与塑性应变—寿命曲线的交点处的寿命2称之为过渡寿命,此点一般作为高、低周疲劳的分界点。由图5发现304SS材料的过渡寿命2大约等于5500,用它作为高低周疲劳的分界点不太合理。这种情况可能是由于异常的2号试验数据引起的,将2号试验数据剔除后,重新对有效试验数据进行回归分析,得到的疲劳寿命参数值如表4所示。

图5 试验结果与回归曲线
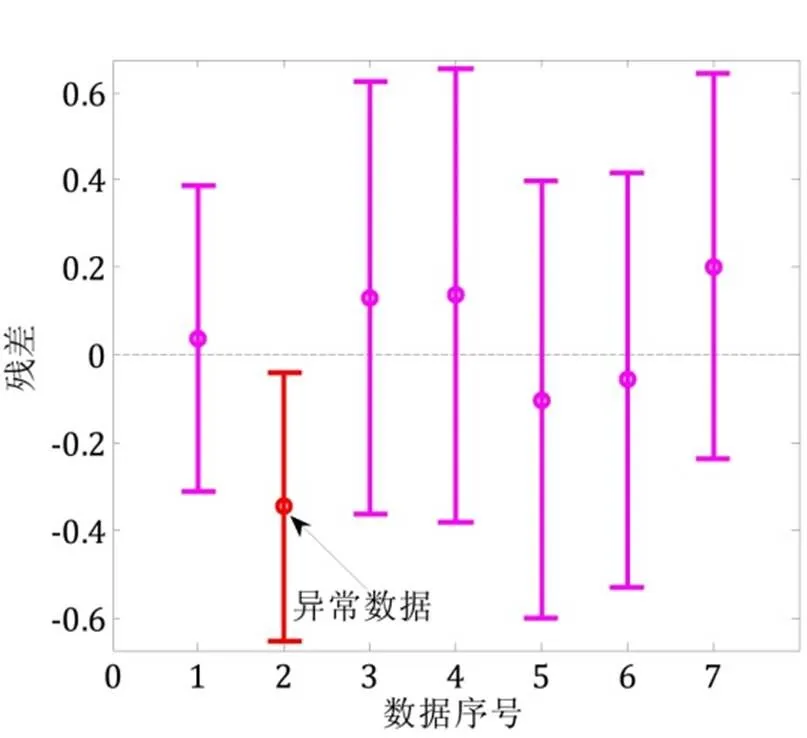
图6 数据残差图

表4 剔除异常数据后的疲劳寿命参数
为了分析剔除异常数据后的计算结果的改善程度,将回归曲线与试验数据绘于图7中。并且对剩余数据再次进行残差分析,发现剩余数据不再表现出异常现象,结果见图8。
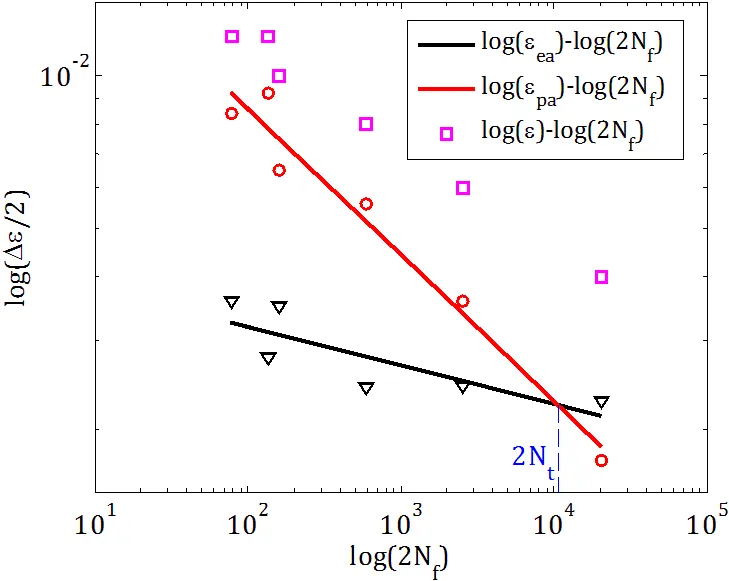
图7 有效数据与新的回归曲线
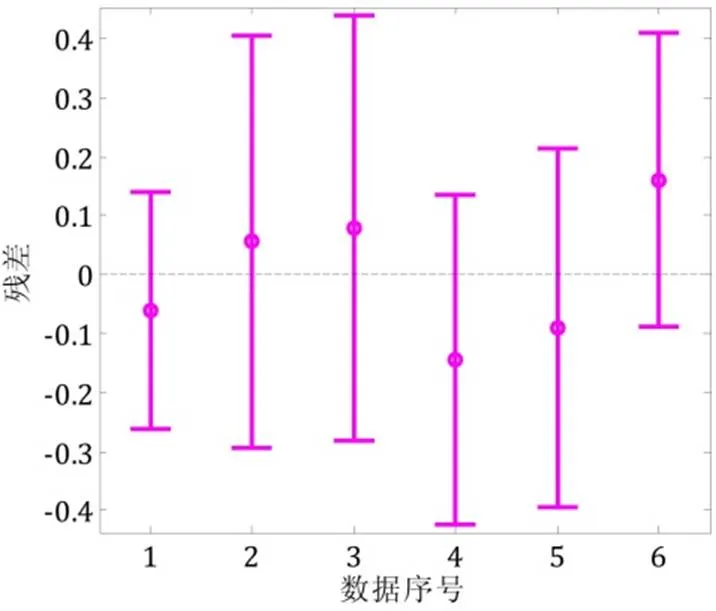
图8 有效数据残差图
剔除2号试验数据后,弹性应变—寿命回归曲线和塑性应变—寿命曲线的相关系数分别为0.670和0.989,这表明曲线对数据的表示能力有了一定的提高。同时,异常数据剔除后过渡寿命2大约为10000,这个结果也在很大程度上得到了改善。目前弹性应变—寿命曲线的相关系数仅有0.670,这可能是由于较少的试验数据引起的,为了提高对高、低周疲劳寿命的预测精度还需开展更广泛的疲劳寿命试验,但鉴于本文的目的是使用304SS来验证叶片疲劳寿命的分析流程,故认为此处的结果是可接受的。
2.2.2 仿真计算
本文所采用的有限元模型和计算边界设置参见文献[7],由文献[7]可知,叶片前缘根部达到最大0.52%的等效塑性应变,为疲劳寿命的关键考核部位。要使试样对应的考核部位达到同等的等效塑性应变,需要在试样夹持段施加大约13407N的机械负荷。利用SWT模型得到试样在应力比为0情况下的疲劳寿命计算结果,如图9所示。
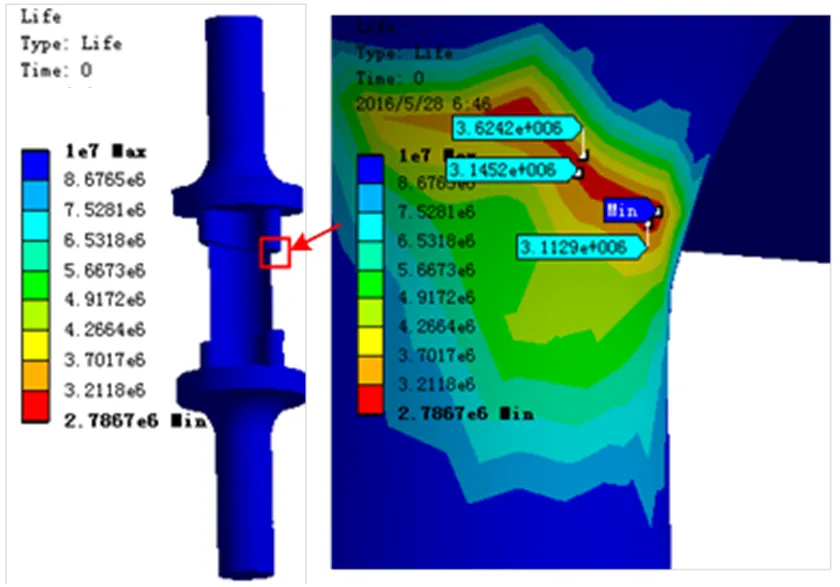
图9 304SS叶片试样寿命分布
由图9可知,叶片试样考核部位的疲劳寿命最少,对应大约2.79´106个工作循环。从理论上来讲,这样高的寿命属于高周疲劳寿命的范畴,但实际涡轮叶片的使用次数远远低于该值。至于该寿命值的准确性与合理性可以通过以下几个方面来分析:
1)疲劳寿命模型参数的准确性。SWT疲劳寿命参数是根据材料疲劳试验数据,利用线性回归分析方法得来的,所以参数值的准确程度受到很多因素的影响,比如试验次数等;
2)考虑到寿命分散性(高周疲劳寿命分散系数达到10)、实际加工状态和使用情况等因素的影响,涡轮叶片的理论疲劳寿命达到如此大的数值是可以接受的。但需要作进一步的疲劳寿命分析以便确定更加合理的疲劳寿命;
3)实际叶片的寿命受高、低周复合疲劳的共同作用,这与一般的低周疲劳表现出来的性质是不同的,它具有更低的疲劳寿命。
2.2.3 试样的疲劳寿命试验
本文开展了304SS叶片试样在离心负荷下的疲劳寿命试验。图10是疲劳试样在疲劳试验机上的夹持状态。根据叶片有限元的计算结果,所开展的负荷控制的疲劳试验条件是:幅值13407N、频率0.25Hz、负荷比为0的三角波。疲劳试验失效判据定义为叶片考核部位出现肉眼明显可见的疲劳裂纹。当试验了10113次循环后,发现叶片前缘根部出现长度约761μm的疲劳裂纹,图11是疲劳裂纹的局部放大图。由图11可知,304SS叶片前缘根部出现761μm的角裂纹,对304SS而言,裂纹的扩展速率低,裂纹扩展至危险裂纹尺寸可能需要一些时间,但如果换成GH4169等高强度合金材料叶片,那么该裂纹的扩展速率将会很快,这在实际应用中是非常危险的。

图10 疲劳试样夹持状态

图11 试样前缘根部裂纹观测结果
对比试验结果与理论计算结果可知,二者相差较大,除了2.2.2节列出的原因,还可能的原因是叶片试样两端施加的负荷是根据有限元仿真计算得到的,叶片前缘根部处于塑性阶段,负荷的较小误差会带来较大的塑性应变误差,故这一负荷的准确性对塑性应变的大小影响很关键,从而对疲劳寿命产生重要的影响。因此,为了尽可能准确地模拟叶片的疲劳寿命,需要在以下几个方面作进一步的深入研究
1)研究带有损伤的材料本构模型,使用仿真的手段直接计算出材料或构件达到的临界裂纹时的疲劳寿命;
2)充分开展材料疲劳寿命试验,通过分析与试验验证的方法提升疲劳寿命模型的预测精度;
3)从理论、试验和经验的角度确定更加合理的寿命分散系数,以使寿命结果涵盖的范围落入包络;
4)要对叶片的设计、加工与使用状态充分了解,这对疲劳寿命的确定与分析也很重要,因为这些资料是确定应力集中因子、疲劳缺口系数、寿命分散系数等的关键;
5)使用应变仪实时准确地测量叶片关键部位的应变值,使试样考核部位的应变值与叶片对应部位的理论应变确实一样,以此来确定合理的试验负荷。
3 结论
本文以某型液体火箭发动机小尺寸冲击式涡轮动叶为对象,从仿真与试验角度建立了叶片疲劳寿命考核方法。首先,利用电液伺服低周疲劳试验机开展了304SS试棒的疲劳寿命试验,在此基础上,利用回归分析的方法对304SS材料的疲劳寿命模型参数进行了识别;然后,利用SWT疲劳寿命模型对叶片离心负荷下的疲劳寿命进行了计算分析,得到考核部位的仿真寿命;最后,结合仿真结果,开展了离心负荷下叶片试样的疲劳寿命考核试验,并对试验结果进行了讨论分析。通过本文的研究主要得出如下结论:
1)利用回归分析得到304SS材料疲劳强度系数'=830.282MPa,疲劳强度指数= -0.076,疲劳延性系数'=0.033,疲劳延性指数= -0.290 ,循环应变硬化系数=2029.434MPa,循环应变硬化指数'= 0.262,塑性应变—寿命曲线的相关系数为0.989,弹性应变—寿命曲线的相关系数为0.670;
2)在13407N拉伸负荷下,叶片试样考核部位与叶片考核部位的等效塑性应变相等同为0.52%,在负荷比0,不考虑疲劳缺口系数条件下,利用SWT模型计算得到的叶片仿真寿命为2.79´106个工作循环;
3)在幅值13407N、频率0.25Hz、负荷比0的三角波循环载荷下,试样经受10113个循环后在叶片前缘根部出现761μm的角裂纹,复现了该型叶片的常见故障模式,仿真结果与试验的差异受疲劳寿命试验数据不充足、模型参数预估不够准确,试样加工表面质量、应力集中等引起的疲劳寿命分散性,实际叶片与模型叶片试验条件存在差异等因素的影响。本文的研究可以为液体火箭发动机涡轮叶片和其他部件疲劳寿命的评估提供参考。
[1] H A Cikanek, Characteristics of space shuttle main engine failures[M]. 1987.
[2] A Abdul-Aziz, R L Thompson, Thermal-structural analysis of space shuttle main engine (SSME) hot section components [M]. 1988.
[3] A Abdul-Aziz, Structural evaluation of a space shuttle main engine (SSME) high pressure fuel turbo pump turbine blade[M].1996.
[4] 郁大照, 温德宏, 张浩然. 某型航空发动机燃气涡轮叶片和盘结构静力学分析[J]. 强度与环境, 2012, 39(4): 32-39. [YU Dazhao, WEN Dehong, ZHANG Haoran. Structural static analysis of gas turbine blade and disk of an aeroengine [J].Structure & Environment Engineering, 2012, 39(4): 32-39.]
[5] D Q Shi, C L Dong, X G Yang. Constitutive modeling and failure mechanisms of anisotropic tensile and creep behaviors of nickel-base directionally solidified super-alloy[J]. Materials & Design, 2013, 45: 663-673.
[6] 王荣桥, 荆甫雷, 胡殿印. 单晶涡轮叶片热机械疲劳试验技术[J]. 航空动力学报, 2013, 28(2): 252-258. [WANG Rongqiao, JING Fulei, HU Dianyin. Experimental setup for testing thermo-mechanical fatigue of single crystal turbine blades[J].Journal of Aerospace Power, 2013, 28(2): 252-258.]
[7] S J Liu, G Z Liang, J C Liu, et al. Research on the fatigue of the small impulse turbine blade based on the numerical simulation and experimental tests [J]. International Journal of Aerospace Engineering, 2021: 1-13.
[8] S Maksimovic. Fatigue life analysis of aircraft structural components [J]. Scientific-Technical Review, 2005(1): 15-21.
[9] S J Liu, G Z Liang, Y C Yang. A strategy to fast determine Chaboche elasto-plastic model parameters by considering ratcheting[J]. International Journal of Pressure Vessels and Piping, 2019, 172: 251-260.
[10] S J Liu, G Z Liang. Optimization of Chaboche kinematic hardening parameters by using an algebraic method based on integral equations [J]. Journal of Mechanics of Materials and Structures, 2017, 12(4): 439-455.
[11] ASTM. ASTM E606/ E606M-12, standard test method for strain-controlled fatigue testing, in Book of Standards[M]. West Conshohocken, PA, USA, ASTM International, 2012.
Research on Fatigue of 304SS Impulse Turbine Blade under Laboratory Condition
LIU Shi-jie1LIU Heng1LIU Ji-chao2LIANG Guo-zhu3ZHANG Jun-wei4WANG Hui1
(1 Beijing Aerospace Propulsion Institute Laboratory of Science and Technology on Cryogenic Liquid Propulsion of CASC, 100076, China; 2 Beijing Machine Tool Research Institute Co., Ltd., Beijing 100102, China; 3 School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing, 102206, China; 4 Beijing Institute of Space Launch Technology, Beijing 100076, China)
There is a growing demand for the fatigue life verification of impulse turbine blades in reusable liquid rocket engines. However, at present, the blade fatigue experiment is mainly carried out with the high cost rocket engine test, and the size of impulse turbine blades is small, so the individual test is difficult. Therefore, the first stage rotor blade of a certain type of oxygen turbine is taken as the research object in the current work. The laboratory assessment method for the fatigue life of small-size liquid rocket engine turbine blade is established, and the feasibility and rationality of the blade fatigue life assessment test from the perspective of theory and experiment is demonstrated as well. A reference for the fatigue life assessment of liquid rocket engine turbine blades and other components was provides in this paper.
Impact turbine blade; fatigue specimen; EDM; reusability; test verification
V416.3
A
1006-3919(2021)02-0038-07
10.19447/j.cnki.11-1773/v.2021.02.006
2021-01-21;
2021-02-25
刘士杰(1985—),男,工程师,研究方向: 火箭发动机可重复使用性,材料力学本构建模;(100076)北京市9200信箱11分箱5号.

