基于粒子群—克里金法的筒段应变场重构与载荷位置识别
胡锡涛 曾捷 李艳芬 严桢锋 冯振辉 孙阳阳
基于粒子群—克里金法的筒段应变场重构与载荷位置识别
胡锡涛1曾捷1李艳芬2严桢锋1冯振辉1孙阳阳3
(1 南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016;2 北京强度环境研究所,北京 100076;3 陆军工程大学 国防工程学院,南京 210007)
针对可重复运载器箭体、燃料贮箱以及飞机机身等筒段类结构健康监测需求,本文提出了一种基于高密度弱反射光纤光栅传感器的筒段结构应变场重构与载荷位置辨识方法。借助ABAQUS有限元仿真软件,得到筒段壁面在载荷作用下的应变场分布特性。研究了基于粒子群—克里金法的壁面应变场重构算法,提升了应变场重构精度。构建了筒段壁面应变场分布式光纤监测与重构系统,借助环向粘贴的高密度弱反射光纤光栅传感器获取壁面离散点的应变信息,结合粒子群—克里金法实现圆筒壁面应变场监测和载荷位置识别(平均定位误差为1cm)。研究结果表明,本文所提方法能够为飞行器筒段结构健康监测、剩余寿命预测以及预测性维修提供技术支撑。
应变场重构;克里金法;粒子群算法;高密度弱反射光纤光栅传感器;载荷位置识别
0 引言
可重复运载器箭体、飞机机身以及燃料贮箱等属于典型飞行器筒段结构[1-2],此类结构在服役过程中承受多种载荷作用,如疲劳载荷、外界冲击力等,还有低温、湿度等严苛的外界环境应力载荷。因此,实现针对筒段结构壁面应力、应变等物理参量的实时监测,能够为航空航天器服役安全评估提供技术支撑。基于光频域反射原理(Optical Frequency Domain Reflection,OFDR)的高密度弱反射光纤光栅传感器技术,在保留光纤光栅传感器优点的基础上,能够显著提高系统的复用容量和空间分辨率[3],使得该技术成为航空航天器结构健康监测领域的热点之一。Munzke D等通过内埋分布式光纤传感器,实现对复合材料压力容器的疲劳状态监测和损伤定位[4]。Ciminello M等采用空间分辨率为5mm的分布式光纤传感器采集复合材料加筋板受冲击下的应变特征,实现结构冲击损伤监测[5]。洛克希德—马丁公司在X-33飞行器机身和低温贮箱表面布置分布式光纤传感器,实现结构表面应变分布在线监测[6]。上述研究工作都是针对结构关键位置进行应变监测,不能给出被测结构整个区域的应变场分布、响应以及受载信息,而这些结构承载响应信息对于结构受载情况辨识与疲劳寿命评估具有重要意义。为此本文以典型飞行器筒段结构为对象,采用光频域反射型分布式光纤传感器,提出一种基于粒子群—克里金算法的飞行器筒段结构应变场重构与载荷辨识方法,并开展了相关试验验证。
1 高密度弱反射光栅传感器原理

基于OFDR原理的分布式光纤解调仪能实现全同弱反射光栅波长信息解调和光栅空间位置查询。文中使用的高密度弱反射光纤光栅传感器,其栅区对应中心波长为1550nm,单个栅区反射率为0.05%,相邻两个栅区间隔为6.33mm,涂覆层材料为有机改性陶瓷。
2 粒子群—克里金法重构原理
2.1 克里金法
克里金插值法(Kriging)是依据协方差函数,对随机场进行空间建模和插值(预测)的回归算法[9]。克里金插值法不仅考虑原始数据点和待插值点的相对位置,还考虑原始数据各点之间的相对位置关系,能够实现线性、无偏和最小估计方差的估计。对于二阶平稳的变量,其方差为
协方差为


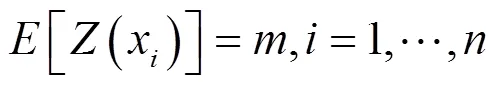
其协方差为
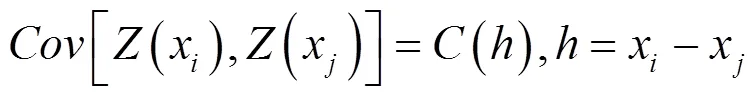
克里金插值的估计公式为[10]


克里金法同时要求误差方差最小,为得到方差最小值,求每个权重的一阶偏导数并使它为0,可得

写成矩阵

2.2 基于粒子群算法的克里金参数优化
本文选用高斯模型作为协方差函数模型,考虑到高密度弱反射光纤光栅传感器在、两个方向传感器密度不同,且反演的是方向的应变场,因此在、两个维度上存在不同的相关性,协方差函数在不同维度上也可能是不同的。设、方向的高斯模型为[11-12]


图2 基于粒子群算法的高斯模型拟合优化流程
3 筒段有限元仿真及重构算法验证
3.1 筒段有限元建模与仿真
以筒段为仿真研究对象,采用ABAQUS仿真分析软件建模,铝合金材质筒段结构高度为1000mm,直径为500mm,壁厚为3mm,上端为开口,底端为封闭,设置材料弹性模量为71GPa,泊松比为0.3,对底面施加固支约束。筒段有限元模型,如图3所示。红色区域尺寸为300mm×300mm,设定为铝合金筒段壁面对应的应变场监测单元。以底面圆心为坐标原点,筒段轴向为轴,建立空间直角坐标系。

图3 筒段有限元模型
假设高密度弱反射光纤光栅传感器沿着壁面环向粘贴,在应变监测单元(红色区域)中共粘贴7行分布式光纤传感器,相邻两行传感器间距50mm,见图4所示。与之相对应,在筒段壁面应变监测单元中设置7条应变提取路径,相邻两条路径间隔50mm,各路径上每隔6.33mm设置一个采样点(对应于高密度弱反射光纤光栅传感器应变测点空间分辨率为6.33mm),共提取48个应变数据。

图4 应变提取路径和加载点位置
集中载荷施加位置可分为两种情况:加载点恰好位于光纤传感器布置路径和位于两行光纤传感器布置路径之间。为此,假设加载点1位于方形监测区域中心,且位于应变提取路径上;加载点2位于两行应变提取路径之间,且与加载点1相距2.5cm,如图4所示。为研究集中载荷作用下,筒段壁面环向应变场的分布情况,先后在加载点1和加载点2位置添加40N集中载荷,方向为径向且指向轴心。当40N载荷作用于不同加载点位置时,对应的仿真应变场结果如图5所示。从图5中可知,在加载点位置存在应变极值,因此可以通过重构筒段壁面受载对应的应变场,计算应变极值点所在位置,进而实现载荷施加位置辨识。

图5 不同加载点位置对应的应变场仿真结果
3.2 基于仿真结果的筒段应变场重构算法验证


图6 载荷对应的群体适应度变化曲线
随着迭代次数增加,群体适应度值快速减小,之后达到种群最优状态。加载点1优化所得相关性系数为(70.3, 1.4),加载点2优化所得相关性系数为(74.4, 1.4)。尽管两个加载点位置不同,但336个应变值组成的样本在两个方向上的空间相关性系数基本不变。7条应变提取路径共包括336个应变值,分别使用粒子群—克里金法和双调和样条法,重构壁面应变监测单元的应变响应分布。为验证两种算法重构精度,提取被监测区域内路径上的应变值,并与数值仿真结果对比,结果如图7、图8所示。
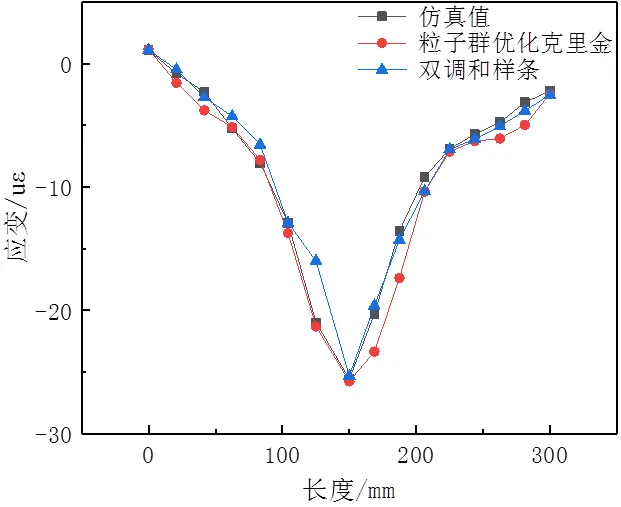
图7 加载点1对应的ab路径重构效果

图8 加载点2对应的ab路径重构效果
从图7和图8中可知,采用7行传感器布局方案时,粒子群—克里金法和双调和样条法重构的应变场均能反映出筒段壁面应变分布特征。对于加载点1,两种算法重构所得应变极值与仿真极值大小一致,且重构路径的极值点所在位置与仿真中载荷施加位置也一致,粒子群—克里金法在应变极值点位置附近重构的应变分布较双调和样条法更加平缓,两种算法在应变极值点附近重构误差增大。对于加载点2,粒子群—克里金法重构所得应变极值大小更加接近仿真所得极值,位置也相吻合。相比之下,双调和样条法重构所得应变极值点在100mm,与实际加载点位置125mm存在稍许差异。两种算法在应变分布平缓位置重构误差较小,越靠近应变极值点位置重构误差越大。由此可知,这两种应变场重构算法也适用于分布压力作用下的筒段壁面应变场重构。对于加载点1,路径上粒子群—克里金法重构应变分布的最大误差为3.8uε,双调和样条法重构应变的最大误差为5.0uε。对于加载点2,路径上粒子群—克里金法重构应变分布的最大误差为2.9uε,双调和样条法重构应变的最大误差为7.3uε。由以上可知,粒子群—克里金法重构效果更优。
4 试验系统构建
为验证基于粒子群—克里金法的应变场重构方法在筒段结构上的可行性,建立如图9所示的筒段壁面应变场重构与载荷位置辨识试验系统。该系统主要由金属筒段、宽带反射镜、OFDR分布式光纤解调仪、电阻应变仪和计算机组成。
在筒段壁面选取一块30cm×30cm的正方形区域定义为应变监测单元,在该区域内布设7行高密度弱反射光栅光纤传感器。每行实际传感长度为30cm,分布48个离散测点,相邻两行光纤传感器间隔5cm。
在第3、4和5行光纤传感器之间等间距设置8个应变测量点,在每个测点粘贴应变片。加载点与应变片的具体位置,如图10所示。在加载点位置施加20N载荷,通过两种应变场重构算法得到路径上的应变分布,将其与应变片实测值进行对比,用以评估两种应变场重构算法的精度。此外,为验证应变场重构算法对载荷施加位置的辨识精度,将整个应变场监测区域划分成31行、11列,共300个长方形网格,每个单元网格几何尺寸为30mm×10mm,如图11所示。

图11 应变监测单元网格划分
以应变场监测单元左下角为坐标原点,建立二维直角坐标系。分别在341个单元网格节点施加20N载荷,通过相关重构算法实现筒段弧形壁面应变场重构。在此基础上,计算该监测单元内应变极值点所在位置坐标,并与实际加载点位置进行对比。
5 试验结果与讨论
5.1 应变场重构效果评估
路径上共有8个应变片测点,这些测点所采集数据反映了该路径上的真实应变分布情况。根据高密度弱反射光栅光纤传感器所测应变数据,分别采用粒子群—克里金法和双调和样条法重构得到路径上应变分布特征,并将其与应变片实测值进行对比,如图12所示。从图12中可以看出,两种算法均能较好反映路径上的应变分布情况,其中粒子群—克里金法重构的应变分布在极值点位置过渡较平缓。当20N载荷作用在加载点时,加载点对应的坐标为160mm,基于粒子群—克里金法重构所得应变极值点对应轴坐标位置为155mm,能够反映出该条路径上的应变分布趋势,而双调和样条法重构所得应变极值点对应轴坐标为150mm。
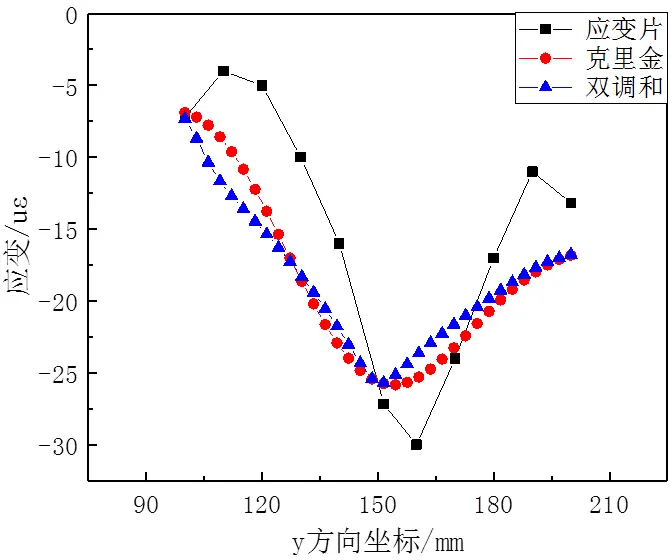
图12 加载点对应两种算法重构误差
以应变片实测数据为参考,两种算法在路径上应变重构的误差结果如表1所示。
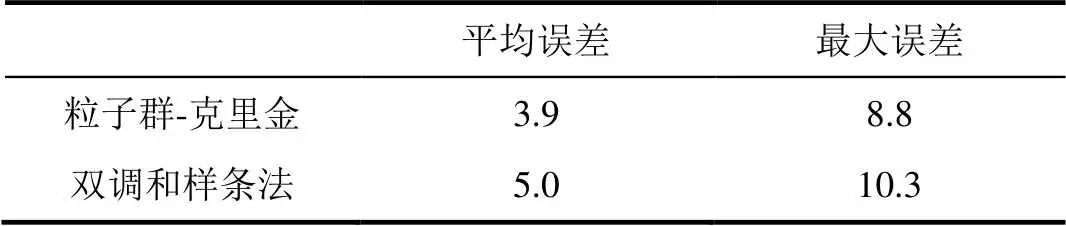
表1 两种重构算法对应的误差对比(uε)
由表1可知,粒子群—克里金法在路径上重构应变的平均误差和最大误差均比双调和样条法小,表明粒子群—克里金法重构效果更优。粒子群—克里金法重构的应变云图如图13所示。
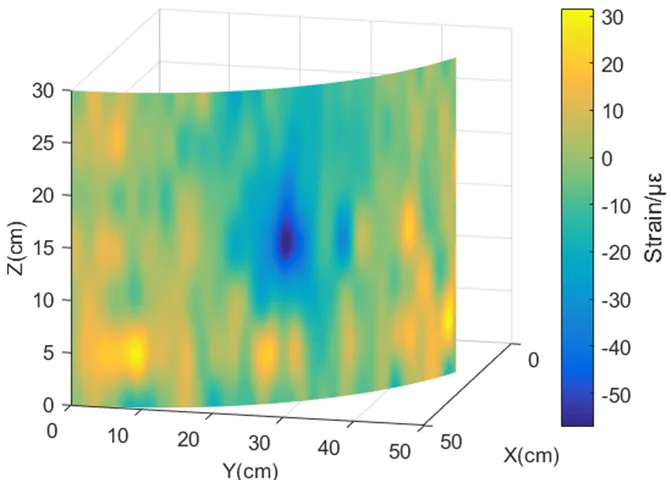
图13 粒子群—克里金法重构所得应变场云图
插值算法中出现的“牛眼”现象是某些偏大或偏小的数据在插值过程中,所形成的以插值点为圆心的圈状现象[14]。从图13中可知,粒子群优化克里金法重构的应变场在竖向上呈条纹状,“牛眼”现象较少,能够反映出加载点位置附近存在应变突变。
5.2 载荷定位效果评估
以基于应变场突变特征辨识获取的载荷施加位置和实际加载位置之间误差幅值为轴变量,以筒段壁面监测单元环向为轴,轴向为轴,将341次模拟加载试验所得定位误差绘制成误差云图,分别如图14和图15所示。

图14 基于粒子群—克里金法的载荷定位误差云图

图15 基于双调和样条法的载荷定位误差云图
从图14和图15可得,当加载位置位于传感器布置路径时,两种算法定位误差均比其它位置小。而随着加载点靠近相邻分布式光纤传感器的中间位置,定位误差逐渐增大。

表2 两种算法对应的载荷定位误差对比/mm
两种算法对于载荷的定位误差对比如表2所示。粒子群—克里金法在整个监测单元上的平均定位误差为10.0mm,双调和样条法定位平均定位误差为12.8mm,两种算法定位误差差异主要来源于粒子群优化克里金法在方向具有更高的辨识精度。
6 结论
本文采用高密度弱反射光纤光栅传感器获取筒段结构应变信息,分别结合粒子群—克里金法与双调和样条法,开展针对筒段壁面应变场重构和载荷位置辨识方法研究,研究结果表明:
1)将高密度弱反射光纤光栅传感器集成于筒段结构,能够提高空间分辨率感知结构受到载荷作用下的应变分布与响应特征;
2)两种应变场重构算法适用于不同应变量级的筒段壁面应变场重构。与双调和样条法相比,粒子群—克里金法重构应变场误差更小。在此基础上,提出了基于应变场突变特征计算的载荷位置识别方法;
3)本文所述方法具有体积小、质量轻、抗电磁干扰等特点,能够为航空航天筒段结构的应变场重构、载荷识别以及结构健康监测提供有益帮助。
[1] 郝鹏. 面向新一代运载火箭的网格加筋柱壳结构优化研究[D].大连理工大学, 2013. [HAO Peng. Research on optimization of grid stiffened cylindrical shell structure for a new generation of launch vehicle[D].Dalian University of Technology, 2013.]
[2] 田智亮, 孙秦. 复合材料加筋筒段压载荷承载能力优化[J]. 航空工程进展, 2014,5(3): 377-382. [TIAN Zhiliang, Sun Qin. Advances in aeronautical science and engineering [J]. Advances in Aeronautical Science and Engineering, 2014, 5(3): 377-382.]
[3] Yuksel K. Complete analysis of multi-reflection and spectral-shadowing cross talks in a Quasi-distributed fiber sensor interrogated by OFDR[J]. IEEE Sensors Journal, 2012, 12(5): 988-995.
[4] Munzke D, Duffner E, René Eisermann, et al. Monitoring of type IV composite pressure vessels with multilayer fully integrated optical fiber based distributed strain sensing[J]. Materials today: proceedings, 2020.
[5] Monica Ciminello, Natalino Daniele Boffa, Antonio Concilio, et al. Damage detection of CFRP stiffened panels by using cross-correlated spatially shifted distributed strain sensors[J]. Applied Sciences, 2020, 10(8).
[6] Schweikhard K A, Richards W L, Theisen J, et al. Flight demonstration of X-33 vehicle health management system components on the F/A-18 Systems Research Aircraft[J]. 2002.
[7] 李政颖, 孙文丰, 王洪海. 基于光频域反射技术的超弱反射光纤光栅传感技术研究[J]. 光学学报, 2015, 35(8): 64-71. [Li ZhengYing, Sun WenFeng, Wang Honghai. Research on ultra-weak reflection fiber grating sensing technology based on optical frequency domain reflection technology [J]. Acta Optica Sinica, 2015, 35(8): 64-71.]
[8] Hideaki Murayama, Hirotaka Igawa, Koji Omichi, et al. Distributed sensing with OFDR and its application to structural health monitoring[P]. Optical Fibre Sensors, 2011.
[9] 周体鹏. 基于克里金插值法的昆明市PM2.5预测[D]. 云南大学, 2016. [Zhou Tipeng. Prediction of PM2.5 in Kunming city based on Kriging inter polation[D]. Yunnan University, 2016.]
[10] 张仁铎. 空间变异理论及应用[M]. 科学出版社, 2005. [Zhang Renduo. Theory and application of spatial variation [M]. Science Press, 2005.]
[11] Søren Nymand Lophaven, Nielsen H B , Jacob Søndergaard. DACE -A MATLAB Kriging Toolbox-Version 2.0[M]. 2002.
[12] 李贵杰, 张晓博, 王璐, 等. 基于Kriging代理模型的失效机会测度算法[J]. 强度与环境, 2020, 47(3):37-42. [LI Guijie, ZHANG Xiaobo, WANG Lu, et al. An efficient algorithm for failure chance measure based on Kriging model[J]. Structure & Environment Engineering, 2020, 47(3): 37-42.]
[13] 刘衍民, 牛奔, 赵庆祯. 多目标优化问题的粒子群算法仿真研究[J]. 计算机应用研究, 2011, 28(2): 458-460. [Liu Y M, Niu B, Zhao Q Z, et al. Particle swarm optimization simulation research on multi-objective optimization problems[J]. Application Research of Computers, 2011, 28(2): 458-460.]
[14] 牛文杰. 基于变异函数的距离加权反比法[J]. 东华大学学报(自然科学版), 2011,37(3): 362-367. [NIU Wenjie. Inverse distance weighting method based on variogram[J]. Journal of Dong hua University (Natural Science), 2011, 37(3): 362-367.]
Reconstruction of Wall Strain Field and Static Load Identification of Tube Section Based on PSO-Kriging
HU Xi-tao1ZENG Jie1LI Yan-fen2YAN Zhen-feng1FENG Zhen-hui1SUN Yang-yang3
(1 State Key Laboratory of mechanical structure mechanics and control, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China; 2 Beijing Institute of Structure & Environment Engineering, Beijing 100076, China; 3 College of National Defense Engineering, Army Engineering University of PLA, Nanjing 210007, China)
In response to the needs of cylinder structure health monitoring, this paper proposes a cylinder structure strain monitoring and strain field reconstruction method based on high-density weak reflection fiber grating sensors. With the aid of ABAQUS finite element simulation software, the strain field distribution characteristics of the wall of the cylinder section under static load are obtained. The wall strain field reconstruction algorithm based on the PSO-Kriging method is studied to improve the accuracy of strain field reconstruction. A distributed optical fiber monitoring system for the strain field on the wall of the cylinder section was constructed, and the strain information of discrete points on the wall was obtained with the aid of a circularly pasted optical fiber sensor. The particle swarm-kriging method is used to monitor the strain field on the cylinder wall and the static load identification. The average positioning error of the static load on the wall is 1cm. The research results show that the method proposed in this paper can provide technical support for aircraft tube structural health monitoring, remaining life prediction and predictive maintenance.
Strain field reconstruction; Kriging; PSO; high density weak reflection fiber grating sensor; load identification
TN913.7; TP212
A
1006-3919(2021)02-0015-07
10.19447/j.cnki.11-1773/v.2021.02.003
2021-02-10;
2021-03-21
航空科学基金(20200009023017)
胡锡涛(1994—),男,硕士研究生,研究方向:新型光纤传感器技术及应用;(210016)南京航空航天大学机械结构力学及控制国家重点实验室.

