高超音速飞行器伸缩机翼的结构设计及稳定性分析

徐晓涵， 刘超

（北京信息科技大学a.光电测试技术北京市重点实验室；b.生物医学检测技术及仪器北京实验室，北京100192）

0 引言

机翼通过变形可以改变翼展、展弦比、浸润面积等几何参数从而影响飞行器的气动参数，使飞行器适应不同的飞行任务[1]。相较于传统固定式机翼，伸缩机翼极大提高了高超音速飞行器的机动性，并有效减小空气波阻力的不利影响，被广泛地应用于巡航类飞机、无人机及其他领域[2-4]。早在1929年，伸缩机翼研究的第一人美国的文森特·加斯特斯·博内利将伸缩机翼的设计理念应用在GX-3飞机上，为提高飞行器的飞行性能提供了新思路[5]。2003年，雷神公司以“战斧”巡航导弹为研究对象提出了伸缩巡航导弹的方案，该研究表明，弹翼展开在导弹巡航时获得了最大升力，俯冲时翼面收缩，导弹的机动性能明显提高[6]。

随着高超音速飞行器进一步高速化和功能多任务化，对可变形机翼的动、静力学性能、气动性能以及环境适应性都提出了更为严苛的要求。伸缩机翼机构的设计正向着结构简单、轻巧的方向发展[1，3-4]，这需要伸缩机构在满足一定的运动、强度和刚度要求的同时，还要尽可能的精简、紧凑。国内外科研人员仍在不断探寻既简单轻巧又能满足飞行器的各种飞行任务的伸缩机翼结构。张伟等[7]设计的伸缩机翼结构以固定机翼为基础，通过丝杆与锥齿轮键连的方式在机翼内部结构上进行改变，探讨了在不同伸缩速度下机翼的振动情况。再如德国航空中心L.F. Campanile等[8]利用可变翼带状肋代替传统翼肋，但在协调带状翼肋的运动上遇到了阻碍。李智、董二宝等[9]将菱形伸缩机构应用到伸缩机翼中，通过对负载状态下的性能进行分析验证了机构设计的可行性。国内外对伸缩机构的设计方案多样，主要有气动伸缩套筒式、钢索拉线式和丝杠带动式[10-12]，这些方案为伸缩机翼设计提供了思路，但不能很好适应高超音速飞行的严苛要求。因此，研究结构简单、稳定可靠的伸缩变形机构是伸缩机翼技术研究的重点内容，同时也极具挑战性。

本文从机构运动学及结构性能方面研究了在高超声速的极端恶劣工作环境中、狭小空间内完成变形的伸缩机翼机构，并分析了其在伸缩变形时的运动学规律、结构的强度，以及各阶模态下的结构变形情况，验证了伸缩机翼机构设计的合理性。

1 伸缩机翼机构设计方案

1.1 技术指标

1）机翼伸缩变形时，机翼面积至少变化50%；2）伸缩机翼设计要满足一定强度和刚度的要求，能够在大承载的环境下保持机翼结构不受损坏；3）在满足强度和刚度和变形要求的基础上，伸缩机翼结构尽可能简单轻巧。

1.2 伸缩机翼设计方案

根据技术指标要求，本文以四连杆机构为基本单元设计了一种伸缩机翼变形结构[13]，通过三维建模软件建立几何模型，其机构运动简图如图1所示、机翼展开时如图2（a）所示、机翼收缩时如图2（b）所示。伸缩机翼变形系统主要由固定翼、前翼肋、后翼肋，以及连杆联动机构这4部分组成。后翼肋CD为原动件（长约470 mm），在电动机的驱动作用下，将推力传递到固定翼的连接杆BC处，然后带动后翼肋AB沿顺时针方向转动，直至前翼肋AB与机架AD（长度约为690 mm）重合，此时机翼由展开状态到达收缩状态，机翼在伸缩过程中机翼面积变形量在70%左右。

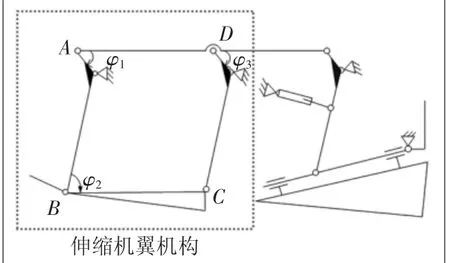
图1 伸缩机翼机构运动简图

图2 伸缩机翼模型伸缩状态图

2 伸缩机翼机构的运动学分析与仿真

2.1 运动学分析

机构某点的轨迹、位移、速度和加速度，以及构件的角位移、角速度和角加速度等运动学参数可以反映整体机构的能效，在机构设计或在机械工作性能分析上有着至关重要的作用。机构运动学分析方法主要有图解法和解析法，图解法形象直观，精度不高。故采用具有较高的精度解析法对伸缩机翼结构进行运动学分析，四连杆机构的矢量封闭模型如图3所示。

根据矢量封闭原则lAB+lBC=lAD+lCD，得出其矢量封闭方程式的复数表达式为

图3 四连杆机构矢量封闭模型

进而得伸缩机翼机构的位移方程为

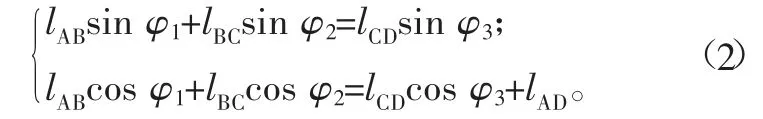
式中：φ1、φ2、φ3分别为前翼肋、固定翼、后翼肋与x轴的夹角（如图1标注所示）。将式（2）对时间t求一阶导，可得伸缩机翼机构的速度方程如式（3）所示。

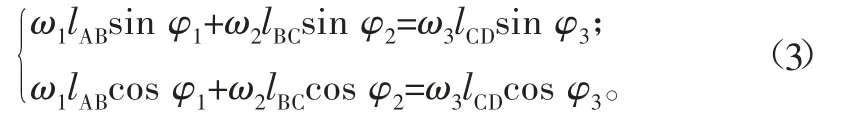
式中，ω1、ω2、ω3分别为各前翼肋、固定翼、后翼肋的角速度。

将式（3）对于时间t求一阶导便可以得到伸缩机翼机构的加速度方程：

式中，α1、α2、α3分别为前翼肋、固定翼、后翼肋的角加速度。

2.2 运动学仿真

采用动力学仿真软件对图2中的伸缩机翼结构进行仿真。图4（a）、图4（b）所示分别为伸缩机翼机构在完成伸缩动作时B点与C点的位移、角速度及角加速度曲线。通过纵向位移变化可以判断B、C两点的位置变化，角速度与角加速度可以反映伸缩机翼机构各部件运动的快慢。仿真可得，当后翼肋CD以360 rad/s的转速运行时，机翼完成收缩用时0.335 s，故伸缩机翼可实现快速变形的要求。

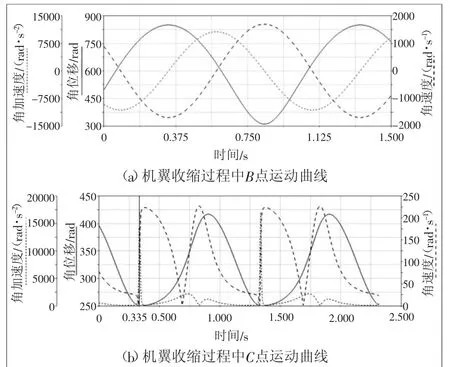
图4 机翼收缩过程中B点与C点运动曲线

3 伸缩机翼机构的性能分析与仿真

3.1 应力分析

在大承载、高超音速的条件下，伸缩机翼翼根处的强度是决定伸缩机翼结构可以稳定工作的重要因素。采用有限元分析软件对伸缩机翼机构进行仿真分析。伸缩机翼机构的材料为铝合金6061，密度ρ=2.7×103kg/m3，弹性模量E=69 GPa，泊松比μ=0.33，屈服强度σ=551 MPa。利用有限元分析软件对伸缩机翼进行静力分析，当温度为150 ℃，负载为1000 N·m时，仿真结果如图4所示，图5（a）、图5（b）分别为前、后翼肋翼根处的等效应力图，由图可见，主要受力部分为翼根处的连接部分，即图2中区域1处，最大等效应力为517.82 MPa，在材料屈服强度以内。综上，伸缩机翼机构符合要求。

图5 区域1处应力分析图

3.2 模态分析

飞行器在飞行过程中不可避免会受到气流冲击的影响，气流的扰动会导致机翼发生扭转变形、弯曲变形或者造成更大程度的损坏[14-15]。任何结构都有其固有频率，当惯性力的激振频率与伸缩机翼的固有频率接近或者相等时，将会使其结构处于不稳定状态。由振动理论可得，伸缩机翼系统的运动微分方程为

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；μ为位移矢量。

本文采用自由振动并忽略阻尼，即阻尼矩阵C可忽略，所以式（5）可以转换为

式中：ω为固有频率，此方程的根为ωi2(i=1,2,3),所对应的特征向量为μi。故无阻尼振动系统的特征方程可以描述为: det=|K-ωM|=0。

结合模态分析理论知识，对变形弹翼各阶模态变形情况进行了仿真，如图6所示，其各阶模态频率如表1所示。由图6可知，在一阶（20.425 Hz）、二阶（52.624 Hz）、三阶（65.731 Hz）振动模态变形条件下，可以看出伸缩机翼主要发生的弯曲变形，距离翼根越远变形程度越大，变形情况主要集中在固定翼BC处，在二阶状态时翼梢处产生变形量最大，变形量的大小与结构的厚度有一定关系，翼肋部分从上到下厚度逐渐减小，变形情况也逐渐加大；四阶（249.920 Hz）、五阶（301.150 Hz）振动模态变形条件下，可以看出伸缩机翼除了发生弯曲变形，还存在一定程度的扭转变形，扭转变形最大的位置在前翼肋AB的顶端，其他部分产生了不同情况的变形。

伸缩机翼的弯曲变形，主要在固定翼及翼肋与固定翼的连接处，轻微的变形在材料可承受范围之内。为了使机构更加稳固，可以增加固定翼的强度及翼肋与固定翼连接处的厚度，如此可以减小轻微的弯曲变形带来的不利影响；伸缩机翼的扭曲变形主要发生在四阶和五阶状态，此时，可以采用增强翼肋结构强度的方法对翼肋进行加固。

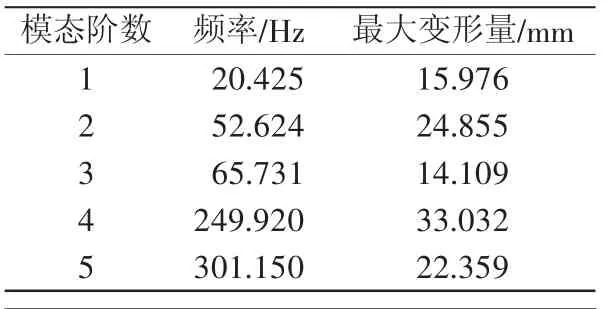
表1 静态条件下的各阶频率

4 结语

本文以平面四连杆机构为基本设计单元，设计了承载大、强度高、机翼面积变形在70%左右的伸缩机翼机构，并从运动学、结构应力和模态的角度对伸缩机翼机构进行了分析，验证了伸缩机翼结构设计的合理性：

1）通过运动学仿真软件对伸缩机翼机构进行分析，得到了 特 征 点B、C 的 位移、速度、加速度等运动学参数，并模拟了在360 rad/s的驱动下伸缩机翼完成收缩动作用时0.335 s，伸缩机翼设计满足快速变形要求。

2）通过有限元分析软件对伸缩机翼的结构进行了仿真，在1000 N·m的负载条件下，伸缩机翼最大等效应力为517.82 MPa，在材料屈服强度以内，伸缩机翼设计符合强度要求。

3）由伸缩机翼机构的各阶模态响应，可得变型翼在不同模态下飞行时的变形情况。另外，伸缩机翼机构在不同模态下的扭转变形情况还与其材料选择有关，材料选择也是值得研究与讨论的问题。

图6 伸缩机翼一至五阶模态图