基于AHP-FCE模型的岩溶地面塌陷灾害易发程度分区评价

李文博，张洪岩，彭 超

(1.深圳市不动产评估中心(深圳市地质环境监测中心)，广东 深圳 518040；2.山东黄金集团有限公司深井开采实验室，山东 莱州 261400)

0 引 言

中国是世界上岩溶最发育的国家之一，近些年随着我国城市化进程的推进，岩溶地面塌陷灾害的发生也呈高发态势，给生产建设活动和群众的生命财产安全带来了重大影响以及损失。岩溶地面塌陷的发育具有隐蔽性、突发性、不均一性以及多因素性等特点[1-2]，因此需要对溶地面塌陷灾害易发程度进行分区评价，并对不同易发程度分区采取相应的措施，防止灾害的发生。

常见的评价方法有专家评议法、灰色系统理论、层次分析法、模糊综合评价法等，每种评价方法都有其优点及适用情况，由于岩溶发育的影响因素较为复杂，因此本文将结合层次分析法(AHP)和模糊综合评价法(FCE)建立岩溶地面塌陷灾害易发程度分区评价模型，并以深圳市东部某学校为例，确定该地区的岩溶地面塌陷灾害易发程度分区。

1 岩溶地面塌陷灾害易发程度分区评价指标

岩溶地面塌陷的形成，通常需要满足3个条件：一是下伏基岩为可溶岩，存在溶蚀的空间(土洞、溶洞)，可以供地下水流动以及塌陷物质的存储；二是上部有一定厚度的盖层，盖层可以是基岩，也可以是土层；三是具有导致岩溶塌陷的作用力。

通过对深圳地区地质环境条件的分析，发现该地区岩溶塌陷主要受基岩条件、地下水条件、盖层条件、构造条件、人为条件和地形地貌条件共6大条件影响，这6大影响条件又是由若干个影响因子共同组成的。本次研究选取6个条件，共计15个因子作为评价因子，见表1。

表1 评价条件层及因子层Table 1 Evaluation condition layer and factor layer

2 岩溶地面塌陷灾害易发程度分区评价的AHP-FCE模型

2.1 层次分析法原理以及权重确定

层次分析法适用于解决存在不确定性和多种评价准则的问题，该方法基于对问题的全面考虑，将定性和定量结合起来，是比较成熟实用的地质灾害易发程度多因素评价方法之一[3-4]。本文将采用层次分析法对岩溶地面塌陷评价的条件层以及因子层进行分析，并得到对应的权重值，实现指标的量化，使评价结果更加客观，然后再使用模糊综合评价法对评价结果进行综合分析，可便捷地评价不同地区岩溶塌陷的易发程度，从而实现岩溶塌陷易发性分区与评价。

通过引入适当的判断标度，将这些判断用数值的形式表示出来，构成判断矩阵，以便比较本层次的各因素与某一因素之间的相对重要性。设B层次中的元素B1、B2、…、Bn与上层次A中的元素Ak有关系，则可以通过判断矩阵表示出来。不同因子间的相互比较结果是利用SATTY[5]提出的1～9标度方法进行打分，不同重要程度分别赋予不同的分值(表2)，可以得到判断矩阵K。

表2 判断矩阵元素Aij的1～9标度方法Table 2 1-9 scaling method of Aij

通过计算得出矩阵K的最大特征根λmax以及对应的特征向量，再进行归一化，可以得到各个评价因素权重集合A={a1,a2,…,an}，同时还要对集合A进行一致性检验，按照式(1)和式(2)进行计算。

(1)

(2)

式中：CI为一致性指标；n为矩阵阶数；CR为随即一致性比率；RI为平均随机性指标，见表3。 当CR<0.1时，则一致性检验通过，否则需要调整矩阵元素取值，直至通过检验。

表3 随机一致性指标Table 3 Random consensus index

2.2 评价条件层及因子层权重计算

由于岩溶塌陷发育受多种因素共同影响，为了更加准确地判断每种因子的影响程度，采用层次分析法分析各因子的权重，为后续分析提供依据。首先计算条件层评判指标的权重，根据1～9标度方法确定B1～B6之间的关系矩阵K见式(3)。

(3)

通过计算可以得到λ0max=6.078 4，CR=0.012 7<0.1，该矩阵满足一致性检验，再计算其对应的特征向量并进行归一化，可以得到式(4)。

AB=[B1,B2,B3,B4,B5,B6]=[0.404 4,0.258 2,0.155 3,0.090 9,0.056 3,0.034 8]

(4)

接下来对因子层指标权重进行计算，以因子层C11为例，C11的判断矩阵K1见式(5)。

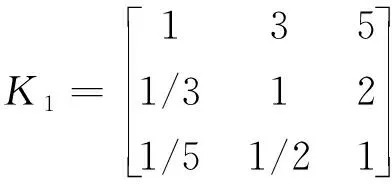
(5)

通过计算可以得到λ1max=3.003 7，CR=0.003 2<0.1，该矩阵满足一致性检验，计算可得式(6)。

ABC=[0.648 3,0.229 7,0.122 0]

(6)

因此，C11单排序权重为AC11=0.648 3，C11的综合权重为A0AC11=0.262 2。

同理，可以计算出所有因子层综合权重，A=[0.262 2，0.092 9，0.049 3，0.139 3，0.076 8，0.042 2，0.095 4，0.041 7，0.018 2，0.060 6，0.030 3，0.037 5，0.018 8，0.023 2，0.011 6]。

2.3 模糊综合评价法原理

模糊综合评价法是一种基于模糊数学的综合评价方法，可以系统性地解决传统方法难以量化的问题，对于非确定性、模糊性的问题有较好的适应性[6-7]。

前文已经得到了所有因子层综合权重集A，为了进行模糊综合评价引入两个集合：①因素集U={u1,u2,u3,…,um}，即评价指标集；②评语集V={v1,v2,v3,…,vn}，即评价结果集。通过对每一个因素ui进行单独评价，可以得到单因素评价集合rij={ri1,ri2,ri3,…,rin}，rij为评语集V的模糊子集。通过对m个因子进行评价可以得到总的单因子评价矩阵R，R=(rij)m×n，可以代表因素集U和评语集V的模糊关系，其中，rij表示因素ui对于评语vj的隶属度。

至此，得到了(U,V,R)模糊综合评价矩阵模型，即可利用最大隶属度原则确定综合评价结果并分类，见式(7)。

B=AR=(b1，b2，b3，…，bn)

(7)

2.4 选取隶属度函数确定模糊关系矩阵

由于本次评价因子层存在连续型指标以及离散型指标，因此对于不同的数据采用了不同类型的函数。对于连续型指标，采用正态型隶属度函数，其表达式见式(8)。

(8)

式中：x为ui的表征指标值；a、c为系数。

在正态分布函数中，一般将研究区域划分n个级别，在给定的分区中点x=a处，u(a)=1，则a是所在区间的平均值；各种评价因子区间端点值处于两种级别之间，对于两种级别的隶属度相同，令其值近似为0.5，见式(9)。

(9)

用a1、a2(其中a1>a2)代表该级别因子的模糊区间端点数值，可以得出式(10)和式(11)。

a=(a1+a2)/2

(10)

c=(a1-a2)/1.66

(11)

本文将岩溶地面塌陷灾害易发程度分为高、中、低三级，分别用Ⅰ、Ⅱ、Ⅲ表示。因此，评语集V={v1,v2,v3,…,vn}={Ⅰ,Ⅱ,Ⅲ}。对于偏小型指标，划分区间为x≤b1，可以认为x取值为[0,b1]，对于偏大型指标，划分x的取值为x>bn-1,此时中点a=bn-1+0.5bn-1。根据式(10)和式(11)以及表4可以计算出因子层隶属度函数系数，见表5。

表4 岩溶地面塌陷评价因子等级划分Table 4 Classification of evaluation factors of karst ground collapse

表5 因子层隶属度函数系数Table 5 Factor layer membership function coefficients

对于中间型指标，要考虑其前后半个区间，如第n-1级别区间[bn-2,bn-1]，可以构建函数见式(12)。

(12)

对于离散型指标(表6)，采用分级的方法来确定隶属度，本次评价指标分为三个等级：高易发级(0.8)、中易发级(0.4)、低易发级(0)。首先根据实际情况给出评定值，再使用梯形隶属度函数，构建隶属度函数见式(13)～式(15)。

表6 离散型评价因子等级划分Table 6 Discrete evaluation factor grade division

(13)

(14)

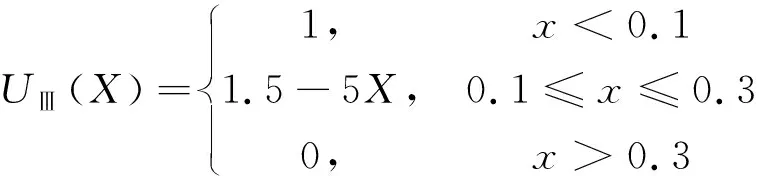
(15)

3 应用实例

深圳市东部地质条件复杂，沿五华深圳断裂北带(企岭吓-九尾岭断裂带)北西盘分布的横岗、坪地、龙岗、坪山、坑梓以及葵涌等第四系盆地底部，有中上石炭统及下石灰统石灰岩(多已变质为大理岩)广泛分布[8]。深圳市可溶岩主要分布在龙岗区、坪山区以及大鹏新区，以深圳东部某学校为例进行计算，该学校周边人行道曾发生一起由于岩溶地质作用以及人为工程活动导致的地面塌陷，岩溶地面塌陷灾害易发程度评价对于保护人民财产安全、开展地质灾害防治工作具有重要意义。

3.1 确定评价指标的隶属度

根据相关资料可以获得评价因子指标，见表7。由表7数据，结合2.4节内容可以得到该处岩溶地面塌陷灾害易发程度分区评价的隶属度矩阵R，见式(16)。

表7 某学校岩溶易发程度分区评价因子指标值Table 7 Index value of the zoning evaluation factor of the karst susceptibility of a school

(16)

3.2 岩溶地面塌陷灾害易发程度分区评价系统

基于本文提出的AHP-FCE模型，采用Python语言，编写开发了岩溶地面塌陷灾害易发程度分区评价系统，并将其嵌入到圳市城市地质三维空间信息平台中，为易发程度分区评价提供计算平台，从而简化了计算过程。

3.3 综合评价

将各因子的取值输入计算模块后，系统会根据AHP-FCE模型中的公式，计算出的所有因子层综合权重A以及隶属度矩阵R，进行岩溶地面塌陷灾害易发程度分区评价。 计算结果为：[0.409 7,0.469 6,0.120 7]。根据隶属度原则，该学校的岩溶地面塌陷灾害易发程度为Ⅱ类(中等易发级)。经实地调查，该评价结果与场地实际情况相符，说明该评价方法合理有效。

4 结 论

1) 本文在研究岩溶发育区影响因素的基础上，基于层次分析法和模糊数学理论，对岩溶地面塌陷灾害易发程度进行评价。通过区分评价因子的类型，确定了连续型和离散型两类因子各自的隶属度函数，实现了定量分析和定性分析的有效结合，从而减少了个人主观判断对评价结果的影响。

2) 建立了AHP-FCE岩溶塌陷灾害易发程度分区评价模型，选取6个条件层共15个影响因子，并确定了各因子的权重：基岩条件>地下水条件>盖层条件>构造条件>人为条件>地形地貌条件。基于上述模型，开发了岩溶地面塌陷灾害易发程度分区评价系统，从而简化了计算过程。

3) 利用AHP-FCE模型，开展深圳东部某学校岩溶地面塌陷灾害易发程度评价，确定该学校的岩溶地面塌陷灾害易发程度为Ⅱ类(中等易发级)，评价结果与现场实际情况相符。表明本文提出的AHP-FCE模型是一种评价岩溶地面塌陷灾害易发程度的实用模型，评价结果准确有效，可以为岩溶地面塌陷灾害的防治提供了依据。