基于自适应Kalman滤波的平面阵列电容成像*

张玉燕 殷东哲 温银堂† 罗小元

1) (燕山大学电气工程学院， 秦皇岛 066004)

2) (燕山大学， 测试计量技术及仪器河北省重点实验室， 秦皇岛 066004)

针对平面阵列电极边缘电场和病态特性严重影响电容图像重建质量的问题， 提出了一种改进的自适应Kalman滤波图像重建算法来同时减小电容及介电常数矩阵的噪声， 在构建引入噪声的平面阵列电容成像状态模型的基础上， 利用极大似然准则来对介电常数矩阵噪声方差阵进行在线估计及实时修正， 并且通过对系统误差协方差矩阵进行动态加权的方法来对此算法的收敛速度进行优化.通过一种复合材料结构件进行缺陷检测实验， 结果表明与LBP， TR正则化及Kalman滤波算法相比， 自适应Kalman滤波算法图像误差最高可降低约20%， 图像相关系数高达0.79， 收敛速度提升约15%， 说明自适应Kalman滤波算法对提升重建图像质量的有效性.此研究对提高平面阵列电容成像的量化精度有着重要意义.

1 引 言

平面阵列电容成像(planar array electrical capacitance imaging)技术是近年来由电容层析成像(electrical capacitance tomography， ECT)技术发展而来的一种新型无损检测技术[1]， 与传统ECT不同， 平面阵列电极传感器是将所有电极排列在同一平面内， 利用电极边缘效应对被测介质敏感， 通过测量电容获得被测空间敏感场介电常数的分布信息， 经过图像重建得到图像灰度值信息.

平面阵列电容成像技术具有灵敏度高、穿透性强、不受被测物几何空间限制等特点[2]， 可以对被测物进行单面检测[3].因此， 该可视化成像技术可适用于陶瓷基复合材料粘接结构的内部粘接层缺陷检测.陶瓷基复合材料在航空航天领域、汽车工业和机械制造领域等具有非常广泛的应用需求， 但由于粘接工艺的原因， 陶瓷基复合材料的粘接胶层会产生一些气泡、孔洞、夹杂等缺陷.这些细小的缺陷可能会造成很严重的安全隐患.而目前还没有成熟的陶瓷基复合材料结构内部粘接层可视化无损检测技术， 因此研究平面电容成像传感技术具有非常重要的意义和实际应用价值.

目前对平面阵列电容成像系统的研究主要包含: 电容传感器的设计[4，5]、3D成像[6，7]及图像重建算法的研究.传统的ECT图像重建算法已经发展得非常成熟， 如: 线性反投影(LBP)[8]、Tikhonov正则化[9]、正交匹配跟踪算法[10]等.虽然传统的ECT图像重建算法有很多地方值得借鉴， 但由于平面阵列电容成像系统“软场”性质更明显， 阵列电极数目和可用数据更少， 因此不适定问题更为严重[11]， 因此高精度的平面阵列电容成像算法对于实现量化检测至关重要.近几年针对平面阵列电容成像算法研究方面， 在文献[12]中， 作者用模糊聚类算法(FCM)直接对电容数据进行聚类处理， 降低了电容数据噪声对图像质量的影响; 在文献[13]中， 作者将Kalman滤波算法应用到平面阵列电容成像中， 通过迭代的方法， 对灰度值和误差协方差矩阵的先验信息不断进行校正， 从而得到最优的灰度值矩阵.在上述两种算法中， 作者均未考虑系统噪声， 但由于平面阵列电极敏感场的“软场”效应，即敏感场的分布是不均匀的， 介电常数矩阵会存在较大噪声， 直接导致图像的伪影非常严重， 影响对缺陷位置及个数的判断.

因此， 为了提高平面阵列电容成像的量化精度， 本文考虑降低平面阵列电极软场性质和不适定问题对图像质量的影响， 提出了一种改进的自适应Kalman滤波图像重建算法来同时降低电容数据及介电常数矩阵的噪声， 并且通过对误差协方差矩阵进行动态加权的方法来对此算法的收敛速度进行优化， 以提高重建图像的精度， 并用模拟复合材料胶层缺陷检测实验验证此算法的有效性.本工作为提升平面阵列电容成像传感技术的量化检测精度提供了强有力的技术依据， 进而推动其在无损检测技术中的可靠应用.

2 平面阵列电容成像原理

平面阵列电容成像系统由电容传感器单元、数据采集单元、图像重建单元三部分组成(见图1).电容阵列传感器单元将被测物场介电常数信息转化为电容的变化值， 数据采集系统采集电容变化值并输入到计算机， 利用图像重建算法在计算机上重建出被测目标的图像[14].

图1 平面阵列电容成像系统Fig.1.Planar array capacitance imaging system.

与传统的ECT不同， 本文所采用平面阵列电容传感器是排列在一个3 × 4的平面阵列中， 共12个电极; 总尺寸为170 mm × 170 mm， 每个电极尺寸为29.8 mm × 40.7 mm， 如图2所示.实验过程中首先激励1号电极， 其余电极作虚地处理，依次测量1—n之间的电容值， 然后激励2号电极，其余电极依然进行虚地处理， 以此类推， 一共可以测得66个电容值.

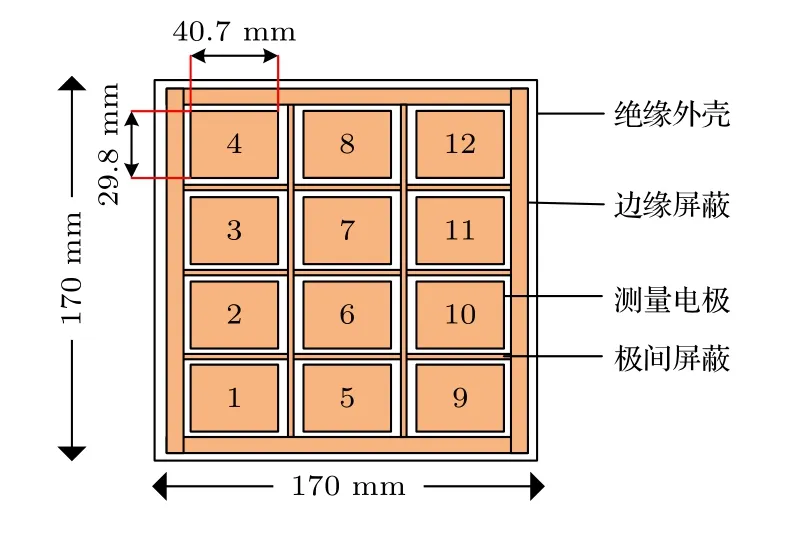
图2 平面阵列电容传感器Fig.2.Planar array capacitance sensor.

平面阵列电容成像方法基于电容的敏感机理，根据麦克斯韦电磁场理论， 在传感器敏感场内的任一点满足(1)式:

式中，D为电位移，ε为介电常数，E为电场强度，B为磁感应强度，ζ为磁导率，H为磁场强度，Je为电流密度，v为电导率.根据Dirichlet边界条件，可以推出平面阵列电容传感器电场微分方程:

其中，ε(x，y) 表 示介电常数，φ(x，y) 表示场域内电势分布.介电常数分布与电容数据的关系为

其中，Г表示电极表面，Q代表电荷，V代表两个电极之间的电位差.对(3)式线性化、离散化和归一化后， 可以简化为下式:

(4)式中，C为归一化后的66 × 1的电容值向量，G为1024 × 1的介电常数矢量， 可看作直接进行图像重建的灰度值;S为66 × 1024的敏感场矩阵， 图像重建问题就是在灵敏度分布矩阵和测量电容数据已知时， 求解(4)式中的G; (4)式中的S反映了介电常数分布不均所导致的电容数据变化率.本文采用有限元的思想来划分电势分布， 从而求得敏感场: 首先将被测场划分为8层， 每层32 ×32个单元， 通过Laplace变换、功率守恒公式及极板表面电荷的分布规律， 可得到i-j电极对在(x，y)处的灵敏度公式:

其中，Vi和Vj为i和j号电极施加的电压激励.Ei(x，y) 与Ej(x，y) 分别表示对i，j号电极施加电压信号时(x，y)处的电场强度;p(x，y) 表示所求解的敏感区域; 然而敏感场的分布是不均匀的， 并受介质分布的影响， 即“软场”性质， 减弱“软场”性质带来的介电常数矩阵噪声是成像的一大难点.

其次， 另一大难点是独立测量的数据C(m=66)要比重建数据的像素值(n= 1024)少很多， 即m≪n， 所以(4)式的逆问题是典型的不适定的、病态的， 求解非常困难.介电常数矩阵噪声及逆问题的病态性会直接导致图像上伪影严重， 甚至会影响判断缺陷的个数， 因此若要提高平面阵列电容成像重建图像的质量， 就必须降低“软场”性质及不适定问题带来的影响.

3 基于自适应Kalman滤波的图像重建算法

3.1 Kalman滤波算法

Kalman滤波算法是一种最优化自回归处理算法， 目前在控制、通信、导航等领域都有着非常广泛的应用.该算法引入状态空间的概念， 充分利用系统的变量初始值、系统噪声等信息， 通过对预测值和测量值不断的迭代， 计算目标的最优估计值，从而得到所需状态向量的最佳拟合值[15].

采用平面阵列电极进行实验时， 由于基于边缘电场工作， 极间电场线较弱， 且易受相互干扰， 测量出的电容变化量数据往往带有很强噪声， 对图像质量有较大的影响.因此需要研究一种既能用于解决平面阵列电容成像的不适定问题， 又能抑制噪声的稳定成像算法.因此Kalman滤波算法能够利用迭代优化解决上述问题.Kalman滤波算法中首先建立该问题的状态空间公式:

假设电极的敏感场分布是均匀的， 只考虑测量时外界因素产生的噪声， 即系统噪声为0， 测量噪声为Vk， 其方差阵为R.Gk为状态估计量， 也就是重建图像的灰度值，Ck表示在k时刻测量后得到的归一化后的电容值;S为敏感场矩阵;Φ表示一个系统矩阵， 其描述了状态向量的演化， 默认为单位矩阵， 所以平面阵列电容成像Kalman滤波模型为

(8)式中，Gk为通过迭代在k时刻得到的灰度值矩阵， 即状态估计值;Pk为在k时刻的协方差矩阵，Kk为k时刻的卡尔曼增益， 整个算法分为预测和校正两大部分， 预测过程是对Gk以及Pk进行先验估计; 校正过程是通过已知预测的先验信息基础上， 对状态矩阵和误差斜方差矩阵进行修正， 并提供反馈， 不断地迭代， 从而得到最优的灰度值状态矩阵[16].

3.2 基于自适应Kalman滤波的图像重建

在上述传统卡尔曼滤波算法中， 为了计算更加简单， 只考虑了测量噪声， 默认该模型中的系统噪声是0， 没有考虑平面阵列电极敏感场“软场”性质带来的影响， 因此会影响成像质量.本文为解决这个问题， 重新考虑系统噪声对灰度值矩阵带来的偏差， 用极大似然准则[17]来估计系统噪声的协方差阵， 并利用新息序列及新息的协方差矩阵对系统噪声协方差矩阵进行实时修正[18]， 依然默认测量电容噪声序列Vk已知， 其方差阵用R表示， 系统噪声序列wk未知， 其噪声方差阵用极大似然法进行估计， 采用Qk表示.整个算法过程如下.

首先建立新的状态空间表达式:

系统的新息序列和新息序列的协方差矩阵分别定义为

其中，vk为新息序列，zk为真实测量值，为测量预测值.若定义为真实灰度值与预测灰度值之差， 则由(9)式和(10)式可得:

灰度值估计误差协方差的一步预测矩阵为

定义α=(Rk，Qk) 为存在噪声的方差阵， 根据极大似然估计准则， 通过新息方差对Qk进行实时的调整[19]， 则目标函数为

由J(α)/∂α可得:

继续分别对(12)式和(14)式中预测参数α求偏导:

当滤波器稳定收敛后， 理论上Pk会趋于常量，并根据Kalman基本关系式[20]可得:

默认电容噪声R的序列已知， 所以令α=R， 将(17)式与(18)式整合后代入到(16)式得:

在整个估计窗内， 若要(19)式成立， 必须满足(20)式的条件[21]:

结合(6)式， 可以推出:

将(21)式代入(20)式可以推导出系统噪声矩阵Qk的自动适应预测估计值:

为了加重新测量的信息在下一迭代过程中的影响， 从而减弱模型对滤波结果的限制， 可使最后一次迭代得到的灰度值最接近理论值， 误差最小，并且在一定程度上抑制滤波发散， 加快收敛速度.实现方法就是对协方差矩阵Pk/k进行动态加权[22]，其基本思想就是随着k时刻Pk/k的不同， 对Pk/k提供不同的加权系数， 实现可变加权， 提高卡尔曼滤波增益的模.系数λk如下:

系数λk逐渐增大并且大于等于1， 当k较小时，a取尽量接近1的值， 当k较大时，a取接近0的值.这样就可以加强对新测量的电容值和灰度值矩阵的修正.

在k=0 时刻， 采用正则化算法得到灰度值G0作为AKF算法迭代的初始值， 根据以往经验， 以及实验验证， 正则化因子为0.1时效果最好.结合(8)式可得动态加权自适应Kalman滤波的平面阵列电容成像公式[23]:

4 实验设计与结果评价

4.1 检测实验设计

本文采用模拟复合材料胶接结构样件中胶层缺陷的检测实验， 验证所提出图像重建算法的有效性.实验材料选取陶瓷基多孔复合材料， 长 × 宽为15 cm × 15 cm、厚度为10 mm， 模拟胶层选取的是16 cm × 16 cm、厚度为3 mm的环氧树脂胶块， 其介电常数与隔热材料相近.测量中电容空场定义为没有胶层的状态(图3)， 满场定义为满胶层的状态(图4)， 传感器单元、数据采集单元和图像重建单元的实物图如图5所示.被测复合材料样件放置在传感器上方， 以非接触方式进行测量.传感电极的电场需要穿透复合材料才能敏感到胶层材料.

图3 无胶层状态Fig.3.Sample without adhesion.

图4 满胶层状态Fig.4.Complete sample.

接下来分别设计4种由简单到较复杂的实验样件， 并分别用LBP算法、Tikhonov正则化算法、传统Kalman滤波算法和自适应Kalman滤波算法来对成像质量进行对比.

样件一为尺寸20 mm × 20 mm的单孔正方形缺陷(图6(a)).样件二为两个尺寸20 mm ×20 mm的斜双孔缺陷(图6(b)).样件三设计为尺寸20 mm×20 mm的上下双孔缺陷(图6(c)).样件四为尺寸20 mm×20 mm的三孔缺陷 (图6(d)).4种样件分别使用传统图像重建算法与自适应Kalman滤波算法得到的重建图为表1所示.图7—图10为归一化后4种样件的测量电容值与满场状态下电容值的差值折线图.

从4种样件的成像效果图来看， LBP和Tikhonov正则化算法生成的图像伪影非常严重， 对于样件四这种较为复杂的缺陷样件， 甚至分辨不出缺陷的个数， 而Kalman滤波算法考虑了外界因素导致的传感器测量的电容误差， 对图像的伪影有些许改善， 但没有考虑系统误差， 图像误差依然很大，样件四的缺陷轮廓较为模糊; 但自适应Kalman滤波算法不仅考虑了电容测量误差， 还用极大似然准则估计了敏感场“软场”性质带来的系统误差， 结果表明对4种样件都有很好的消除伪影的效果， 能清晰地分辨出缺陷的个数， 下文将从重建图像误差、图像相关系数对4种算法生成的图像质量进行对比.

图5 (a)传感器单元; (b)数据采集单元; (c) 图像重建单元实物图Fig.5.(a) Sensor unit; (b) data acquisition unit; (c) physical image of image reconstruction unit.

图6 样件一(a)、二(b)、三(c)、四(d)示意图Fig.6.Schematic diagram of sample I (a)， II (b)， III (c) and IV (d).

图7 样件一电容差值折线图Fig.7.Capacitance difference of sample I.

图8 样件二电容差值折线图Fig.8.Capacitance difference of sample II.

图9 样件三电容差值折线图Fig.9.Capacitance difference of sample III.

图10 样件四电容差值折线图Fig.10.Capacitance difference of sample IV.

表1 不同算法成像效果图Table 1.Imaging effects of different algorithms.

4.2 图像质量评价

在得到重建图像之后， 一般用重建图像误差Ie和图像重建相关系数Ic来对图像的质量进行评价.Ie是指图像重建之前与重建后的灰度值矩阵向量的相对误差值，Ie越小， 图像的质量就越高， 其公式为

其中，G为初始的图像的灰度值矩阵;为重建迭代后的灰度值矩阵.Ic指原始的缺陷图像与经过算法重建后的图像灰度值向量之间的相关度，Ic越大重建后的图像与原始的图像就越接近， 图像质量也就越高， 评价公式为

4种样件分别用上述4种算法得到的图像误差和图像相关系数对比分别如表2和表3所示.

表2 不同算法图像误差对比Table 2.Image error comparison of different algorithms.

表3 不同算法图像相关系数对比Table 3.Comparison of image correlation coefficients of different algorithms.

从表2和表3可以看出， 对于4种样件， AKF算法相比于其他3种算法， 图像相关系数都有较大提升， 图像误差有明显降低， 尤其对于样件四这种较为复杂的缺陷样件， LBP， TR算法的图像相关系数仅仅在0.25左右， 而AKF算法依然可以在0.6以上， 提升近60%， 由此可以说明越是复杂的缺陷， 电场线更容易受到干扰， 敏感场“软场”性质更严重， 所以AKF算法的优势就更明显.

由于真实的工程测量环境要比在实验室更复杂， 电容噪声和敏感场噪声更大， 为了更加贴近实际的工业环境， 我们在电容数据和敏感场矩阵同时被扰动的情况下对KF和AKF两种迭代算法前100次迭代的图像误差进行对比， 从而判断收敛速度.首先定义电容数据噪声水平Ec和敏感场噪声水平Es:

图11 样件一图像误差Fig.11.Image error of sample I.

图12 样件二图像误差Fig.12.Image error of sample II.

图13 样件三图像误差Fig.13.Image error of sample III.

图14 样件四图像误差Fig.14.Image error of sample IV.

对于4种样件， KF算法以及AKF算法完成收敛所需要的迭代次数以及完全收敛后的图像误差如表4所示.通过图11—图14及表4可以分析出， 在电容数据和敏感场矩阵同时被扰动的情况下， AKF算法相比于KF算法， 依然可以用更少的迭代次数完成收敛， 并且收敛后的图像误差有明显降低.从而进一步说明AKF算法在收敛速度和滤波精度上都有较大提升.

表4 不同算法收敛速度对比Table 4.Comparison of convergence speed of different algorithms.

5 结 论

本文提出了一种改进的自适应Kalman滤波图像重建算法来解决平面阵列电容传感技术检测复合材料构件粘接缺陷的成像问题， 并通过复合材料粘接构件进行缺陷检测.实验结果表明， 所提算法对平面阵列电极严重的不适定成像条件有较好的适应性.本文算法采用极大似然法估计平面阵列电容成像模型的噪声方差阵， 有效降低了测量电容噪声及电极敏感场“软场”性质带来的介电常数矩阵噪声， 使图像误差相较于其他几种算法最高可降低20%， 重构图像相关系数高达0.79， 并且通过对误差协方差矩阵进行动态加权的方法来对此算法的收敛速度进行优化， 收敛速度提升近15%.此研究为提高平面阵列电容成像检测的量化精度提供了强有力的技术依据.后续将进一步考虑复杂被测物场条件下的图像重建.