巨梯型四能级里德伯原子系统透射光谱性质的调控*

高小苹 梁景睿 刘堂昆 李宏 刘继兵†

1) (湖北师范大学物理与电子科学学院， 黄石 435002)

2) (湖北师范大学， 光电技术与材料湖北省重点实验室， 黄石 435002)

采用超级原子模型研究了一个巨梯型四能级里德伯原子系统与一个弱光场和两个强控制场的相互作用.利用蒙特卡罗算法， 通过数值求解海森伯-朗之万方程， 讨论了系统的动力学演化， 研究了偶极-偶极相互作用对探测场透射谱和二阶强度关联函数的影响.在有限温度下， 利用洛伦兹分布函数代替麦克斯韦分布函数，得到解析的探测场极化率， 讨论了强场的失谐量对系统出射探测场透射谱对称性质的影响， 最后研究了多普勒效应对探测场透射谱和二阶强度关联函数的影响.结果表明， 在电磁诱导透明条件下， 透明窗口处出射探测场的透射率随着入射探测场强度的增强而减弱， 而当系统入射探测场强度不变时， 通过改变强场的失谐量可以得到非对称的透射谱.此外， 当弱探测场和强场的传播方向一致时， 多普勒效应对系统透射谱和二阶强度关联函数的峰值有很小的影响.当探测场和强场的传播方向不一致时， 多普勒效应对系统透射谱和二阶强度关联函数的影响可以忽略.

1 引 言

偶极-偶极相互作用是极性分子间最普遍的一种相互作用.里德伯原子系统中具有较强的偶极-偶极相互作用， 可用于量子计算中的多量子比特操作， 进而实现复杂的量子操控.因此吸引了大量的科研工作者从事相关研究.比如， 利用偶极-偶极相互作用可以研究不同原子能级之间的纠缠动力学问题[1—4]、实现可控的量子门方案[5]以及量子纠缠[6，7].除此之外， 对原子-分子相干操控[8，9]、慢光控制[10]、可控光栅[11，12]、以及原子系统的光学双稳性[13]、非线性孤立波[14—17]、玻色爱因斯坦凝聚体的结构和磁化率等方面的研究也有促进作用[18—21].里德伯原子之间的偶极-偶极相互作用非常强， 利用电磁诱导透明技术， 可以实现单光子巨克尔效应[22—24].利用超级原子模型理论方法[25—27]求解里德伯原子系综的光学响应问题， 将超级原子模型计算出的透射强度与实验结果[28]进行对照， 结果表明两组结果符合得非常好.利用干涉仪， 在三能级梯型系统中测量了系统的色散特性[29]; 在N型系统中实现了单光子开关[30]; 在倒Y型系统中， 实现了线性电磁诱导透明和非线性电磁诱导透明两窗口的分离， 并且通过调节探测场强度实现了透射光谱由对称向不对称的转换[31]; 在四能级梯型系统中发现， 当系统满足共振条件时， 出现无多普勒中心吸收的现象[32].

在有限的温度下， 利用洛伦兹分布函数， 研究了二能级冷原子系统单光子里德伯激发， 发现原子温度越高， 多普勒展宽可以减小双稳态区域[33]; 对三能级梯型里德伯原子模型进行改进， 讨论了三能级里德伯冷原子系统的相干效应， 结果表明在低温下多普勒展宽会削弱探测光的的非经典性质[34];利用数值计算方法， 讨论了多普勒效应对分子磁体介质中透射光栅的影响[35，36].在四能级Y型系统中， 当探测场的拉比频率增加时， 探测场的电磁诱导透明会转化为电磁诱导吸收[37]; 英国和美国的小组在四能级梯型里德伯原子系统中观察到了电磁诱导透明， 探测光谱呈现亚多普勒特征， 由于交流斯塔克位移补偿了多普勒频移， 可以实现光谱增强[38].国内的研究小组[39]提出了一个实验上可行的方案， 通过三步级联激发控制稳态里德伯态布局， 该方案与传统的双光子电磁诱导透明不同， 稳态里德伯态布局由两个耦合场之间的相对强度决定， 而不取决控制场的绝对值.在此基础上， 本文讨论了不同强度入射探测场对里德伯原子系统的透射谱和二阶强度关联函数的影响， 计算了失谐量对系统对称透射谱影响， 最后给出有限温度下透射谱和二阶强度关联函数随探测失谐量的变化曲线.

2 理论模型

考虑图1所示的巨梯型四能级原子系统[39]，由基态|g〉， 亚激发态|k〉， 激发态|e〉和一个里德伯态|r〉组成.一个频率为ωp的探测场驱动跃迁|g〉到|k〉， 其拉比频率为而两个频率为Ωc1和Ωc2的控制场分别驱动跃迁|k〉到|e〉和|e〉到|r〉， 对 应 的 拉 比 频 率 分 别 为Ωc1=Ec1μke/(2ℏ) 和Ωc2=Ec2μer/(2ℏ).其中Ec1和Ec2分别描述第一个控制场的振幅和第二个控制场的振幅，μxy(xy=g，k，e，r)表示|x〉→|y〉跃迁的电偶极矩，表示探测场的振幅算符，V表示里德伯原子的量子探测体积， 考虑偶极-偶极相互作用， 系统的哈密顿量可以表示为

其中，表示四能级原子的哈密顿量，表示四能级原子与三个场的相互作用哈密顿量，表示范德瓦耳斯偶极-偶极相互作用哈密顿量，表示第i个原子的投影算符，Rij表示i原子和j原子之间的距离.δp=ωp-ωkg表示弱探测场的失谐量，δe=Ωc1-ωek和δr=Ωc2-ωre分别表示两个控制场的失谐量.

图1 里德伯原子系统能级示意图， 一个失谐量为 δp 的弱探测场驱动基态到亚激发态的跃迁， 第一个失谐量为 δe 的强控制场驱动亚激发态到激发态的跃迁， 第二个失谐量为δr 的强控制场驱动激发态到里德伯态的跃迁.实际能级基于铯原子选取Fig.1.General energy level diagram for four levels Rydberg atomic system.A weak probe field， detuned from the intermediate level by δp ， drives transitions from the ground state | g〉 to the intermediate state | k〉.The first strong control field， detuned from the intermediate level by δe ，drives transitions from the intermediate state | k〉 to the excited state | e〉.State | r〉 is a Rydberg state directly coupled to state | e〉 by the second strong control field Ω c2.Real energy levels are shown based on Cs atoms.

假设弱探测光沿着Z轴方向传播，σ^μν(r) 表示处在Z处微小体积 ΔV内的所有的平均值， 利用弱场近似， 可以得到如下海森伯-朗之万方程(令ℏ=1):

式 中Δ1=γgκ+iδp，Δ2=γge+(iδp+iΔe)，Δ3=γgr+(iδp+iδe+iδr) ， 其中γgk，γge，γgr表示相应能级的衰减率.表示由于范德瓦耳斯作用引起的里德伯态|r〉的总位移.在稳态条件下， 假设原子最初状态处在基态|g〉，有采用绝热近似条件消除， 可以得到

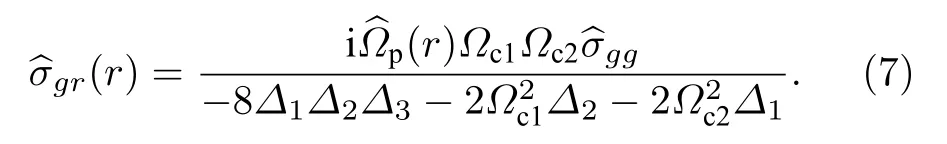
借助超原子概念， 在偶极阻塞机制下， 一个超原子内部只有一个原子被激发到里德伯态|r〉， 每个超原子的体积是偶极阻塞半径[25]， 在这个模型中， 超原子的阻塞半径Rb=超原子之间没有偶极相互作用， 因此原子样品可以看作是由无偶极相互作用的超级原子组成的.假设原子局域密度为ρ(r) ，则单个超原子中含有的平均原子数目nSA=ρ(r)VSA.

根据超级原子的定义， 每个超原子结构中含有很多集体态， 但是每个超原子中最多有一个原子被激发到里德伯态|r〉， 仅用四个集体态就可以很好地描述巨梯型原子系统， 即

则系统中探测场的极化率:

其中α3和α4分别表示梯型和巨梯型原子的极化率， 通过在稳态时求解方程(3)—方程(6)， 可以得到α3和α4的表达式如下:

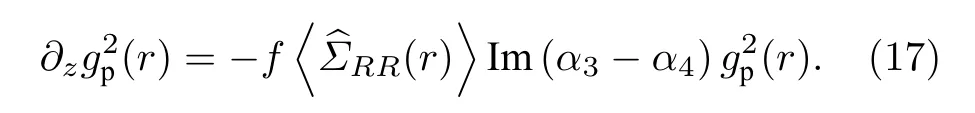
为了了解系统演化的详细信息， 采用蒙特卡罗方法数值求解方程(13)—方程(17).首先在传播方向上求出超级原子的个数L/(2Rb) ，L为原子样品的长度，Rb为超级原子半径.其次， 在每个超级原子处产生一个随机数pz∈[0，1] ， 如果则令表明超级原子内部有一个里德伯原子被激发， 此时系统表现为巨梯型原子系统.反之，系统超级原子内部没有里德伯原子被激发， 表现为普通三能级梯型原子系统.最后， 重复多次这样的独立过程， 然后对所有的数值结果取平均值.数值计算过程中采用Monte-Carlo方法， 可以保证系统状态接近真实的原子随机分布情况， 进而保证数值计算的可信度.

3 理论与数值计算

本文采用真实的超冷Cs原子参数[39]， 具体取值为Ωc2/(2π)=10 MHz， 激光线宽为 0.5MHz.原子的密度遵循分 布， 其中峰值为ρ0=1.32×1 07mm-3且半峰宽度为σz=0.7mm.超级原子模型封锁半径为Rb=4.58 μm，每一个超级原子内含有的原子个数为nSA≈4.7 ，那么100个SA原子组成的介质长度为L=0.9 mm.

图2(a)给出了在不同初始探测光强度下的透射光谱随单光子失谐量δp的变化图， 变化趋势与梯型三能级里德伯原子系统中的结果类似[24].在图2(a)中可以清楚地观察到在δp/(2π)=±5MHz处有两个透明窗口， 在透明窗口处随着探测光场强度的增加， 透射率逐渐降低， 对应的EIT窗口受到抑制，Ip(L)/Ip(0) 最大值在0.3—0.6之间， 表明由于范德瓦耳斯相互作用导致的非线性效应起到主要的作用.图2(b)表明随着探测光强度的增大， 在透明窗口处， 光子的反聚束效应逐渐增大， 当Ωp/(2π)=4MHz 时， 二阶强度关联达到=0.6.有限温度情况下， 考虑多普勒效应对系统透射和二阶强度关联函数的影响.假定原子沿着Z轴传播， 其运动速度分布遵循麦克斯韦分布规律， 在计算时，要做如下更改:δr+κ3v，其 中κ1，κ2，κ3为 对 应 的 波 失， 且κ1=wp/(2π)，κ2=we/(2π)，κ3=wr/(2π).则多普勒效应下系统的极化率可以改写为

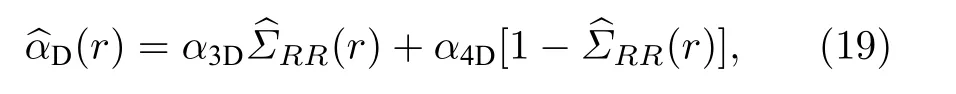
其中α3D和α4D的表达式为

其 中ΔF=iκ1+iκ2，B1=Δ1ΔF+iκ1Δ2和D1=表 达 式 详见附录A.

图2 (a)透 射函数 I p(L)/Ip(0) 随 δ p/(2π) 变化的 曲线， 三条线对应不同的初始探测场 Ω p/(2π)=0.1，2.0，4.0 MHz;(b)对应的探测场的二阶强度关联函数 随δp/(2π) 变 化 的 曲 线， 其 他 参 数 取 值 分 别 为 δ e=δr= 0 ，Ωc1/(2π)=Ωc2/(2π)=10MHzFig.2.(a) Probe field transmission I p(L)/Ip(0) versus detuning δp ， for different input intensities corresponding to Ωp/(2π)=0.1，2.0，4.0MHz; (b) corresponding intensity correlation functions .Other parameters are δe=δr=0 ， Ω c1/(2π)= Ω c2/(2π)=10 MHz.

图3 探 测 光 和 控 制 光 同 向 传 播 时， (a)透 射 函 数Ip(L)/Ip(0) 和(b)光子二阶强度关联函数随 δp 的变化， 其中 δ e=δr=43 MHz， Ω p/(2π)=1.5 MHz，Ωc1/(2π)=Ωc2/(2π)=10 MHz， 实 线 表 示 T =0.3K ， 虚线表示 T =0 KFig.3.When probe and control fields travel in the same direction， (a) the transmission of probe fieldIp(L)/Ip(0)and (b) the corresponding intensity correlation functionsversus the probe detuning δp.Other parameters are selected as δ e=δr=43 MHz，Ωp/(2π)=1.5 MHz， Ω c1/(2π)=Ωc2/(2π)=10 MHz.The solid curve denotes T =0.3 K， and the dashed curve denotes T =0 K.

图4 探 测 光 和 控 制 光 反 向 传 播 时， (a)透 射 函 数Ip(L)/Ip(0) 和(b)光子二阶强度关联函数 随 δp 的变化， 其中 δ e=δr=43 MHz， Ω p/(2π)=1.5 MHz，Ωc1/(2π)=Ωc2/(2π)=10 MHz， 实 线 表 示 T =0.3 K， 虚线表示 T =0 KFig.4.When probe and control fields travel in opposite directions， (a) the transmission of probe fieldIp(L)/Ip(0)and (b) the corresponding intensity correlation functions versus the probe detuning δp.Other parameters are selected as δ e=δr=43 MHz，Ωp/(2π)=1.5 MHz， Ω c1(/2π)=Ωc2/(2π)=10 MHz.The solid curve denotes T =0.3 K， and the dashed curve denotes T =0 K.

光同向传播的条件下， 图3给出了T=0K 和T=0.3K时透射函数和二阶强度关联函数随着单光子失谐量δp的变化图.图3(a)与图2(a)对比可知， 当 调 节 失 谐 量 (δe，δr) 的 值 从0 MHz变 为43 MHz时， 系统的对称透射谱转变为非对称透射谱， 而且透射率相对于图2(a)的透射率略高， 在δp=0MHz 的右侧几乎没有光透过， 造成这一现象的原因是失谐量可以影响范德瓦耳斯力产生的能级移动.当两束控制光反向传播时， 图4给出了T=0K 和T=0.3K 时透射函数和二阶强度关联函数随着δp的变化图.可以看出，T= 0 K和T=0.3 K的两条曲线基本重合， 表明调节控制光的传播反向， 可以有效消除多普勒效应对透射谱和二阶强度关联函数的影响， 原因是当反向传播时， 由于λp，λc1和λc2相差不大， 三光子失谐中-κ1ν+κ2ν相互抵消， 多普勒效应的影响可以被抵消[34].

4 结 论

本文研究了巨梯型四能级超冷里德伯原子系统与三个光场的相互作用， 通过调节两束强光强度和失谐量， 可以有效调节弱探测光场的透射谱和二阶强度关联函数， 随着弱探测场的初始强度的增加， 透明窗口处探测场的透射率减小， 表明里德伯态之间偶偶相互作用导致系统的非线性效应增强且起主要作用.选取合适的控制场强度， 当失谐量由δe=δr=0 ， 改 变 为δe=δr=43MHz 时， 系 统可透射谱由对称变为不对称.最后考虑多普勒效应对系统透射谱的影响， 为了准确评估多普勒效应的影响， 在积分时采用洛伦兹分布函数M(v)=代替克斯韦速度分布函数， 得到了系统解析的探测极化率.研究结果表明， 在低温条件下，当探测光和控制光同向传播方时， 多普勒效应对系统透射的影响主要集中在透明窗口处.当光场异向传播时， 多普勒效应对系统的透射谱和二阶强度关联函数的谱线几乎重合， 即通过控制光的传播方向， 可以有效消除温度对系统的影响.

附录A

K1，K2，K2表达式如下:

对应的B2，C2，E，F，G，E1和E2的表达式如下: