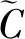非自治Cahn-Hilliard方程的指数吸引子

张晓雨，姜金平

(延安大学 数学与计算机科学学院，陕西 延安 716000)

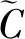
本文受文献[4]和文献[6]的启发，研究了当含有外力项g(x,t)时，如下有界区域上非自治Cahn-Hilliard方程指数吸引子的存在性：

ut+v△2u=△f(u)+g(x,t)，(x,t)∈Ω×(0,∞)，

(1)

u=△u=0，(x,t)∈Ω×(0,∞)，

(2)

u(x,τ)=uτ(x)，t>τ0。

(3)

其中Ω⊂Rn(n≤3)是具有光滑边界的有界区域，g(x,t)是依赖于时间t的外力项，是关于t的几乎周期函数，当g(x,t)=0时，是自治Cahn-Hilliard方程。

非线性项f满足：

f′(u)>-k,F(u)>u，

(4)

存在0<γ≤β≤∞使得

|f′(u)|≤k1(1+|u|β)，

|f″(u)|≤k2(1+|u|γ)。

(5)

1 预备知识

本文用C,C0,C1,C2…表示依赖于Ω和n的常数，令H=L2(Ω)，Lp(Ω)和Hs(Ω)中的范数分别记作|·|p和‖·‖S，特别地，|·|=|·|2，‖·‖=‖·‖2。Cb(Ω×R,X)表示在Ω×R上且取值于X上的有界连续函数的全体，B(X)表示X中的有界集合的全体，

(，·，)表示H的内积，A=-△。

定义1[6]设X是一个度量空间，半群S(t)：X→X，集合M⊂X，如果满足：

1)紧集M⊂X，并有有限分形维数；

2)集合M是正不变集，即S(t)M⊂M；

3)集合M是一个指数吸收集，即存在一个常数l>0，使得对任意有界子集B⊂X，存在一个常数k=k(B)>0，使得dist(S(t)B,M)≤ke-lt。

则M称是半群S(t)的指数吸引子。

定理1[3]设X是一个Banach空间，S(t)是X上的半群，如果满足：

1)S(t)存在一个有界吸收集B⊂X；

∀x∈B,t≥T。

则S(t)存在指数吸引子。

2 指数吸引子的存在性

定理2 设f(u)满足条件(4)和(5)，g(x,t)∈Cb(Ω×R,H)，则方程(1)—(3)存在唯一解U∈V。

定理2的证明详见文献[8]。

定理3 设g(x,t)∈Cb(Ω×R,H)且条件(4)和(5)被满足，半群S(t)在空间V中有有界吸收集，即对中任意的有界集B，存在t1(B)>0,ρ1>0，使得∀u1∈B有：

|u1(t)|2≤ρ12，∀t≥t1。

(6)

证明用u1与方程(1)作内积，可得：

(△f(u),u1)+(g(x,t),u1)。

(7)

又(g(x,t),u1)≤|g‖u1|≤

(8)

再结合式(5)，可以得到：

(9)

对式(9)进行整理得:

(10)

结合Poincare不等式，可得

(11)

利用Gronwall引理，得到

|u1(t)|2≤ρ12，∀t≥t1。

(12)

定理4 设f满足式(2)和式(3)，g∈Cb(Ω×R,H)，那么S(t)在V上存在指数吸引子。

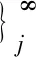
令Vm=span{ω1,ω2，…,ωm}⊆V，Pm:V→Vm是一个正交投影算子，对于任意u∈N，记

u=Pmu+(I-Pm)u=u1+u2。

用-△u2与式(1)作内积，可得

(△f(u),-△u2)+g(x,t),-△u2)。

(13)

因为(△f(u),-△u2)=(▽f(u),▽△u)=

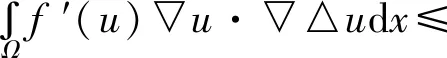
(14)

(15)

把式(14)和式(15)代入(13)可以得到

(16)

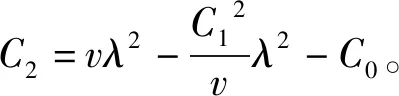
由引理2及Poincare不等式，可以得到：

利用Gronwall引理，则有

当m→∞时，λm→∞。

定理5 设在有界区域上f满足条件(4)和(5)，g∈Cb(Ω×R,X)，那么在满足方程(1)—(3)的条件下，半群S(t)在V上有指数吸引子。