某重载型相控阵天线车稳定性设计
孟庆芹,李伟才,杨春鹏,周含宣
(中国船舶集团有限公司第八研究院,南京211153)
0 引 言
本文以空间力系的平衡方程为理论依据,推导出天线车失稳临界力系平衡方程,用于某重载型相控阵天线车的稳定性计算,并通过仿真手段予以验证。
1 空间力系的平衡方程[3]
根据力学经典理论,如图1所示,当空间各力在三个坐标轴中每一个轴上的投影的和等于零,以及这些力对于每一个坐标轴的矩之和也等于零时,该组力系处于平衡状态。空间任意力系的平衡方程组如下:
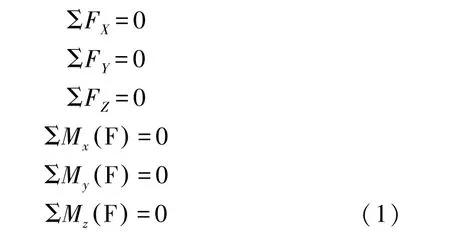
2 天线车失稳临界力系平衡方程
根据天线姿态不同,天线车一般分为运输姿态和工作姿态进行稳定性计算:运输姿态下,天线车各部分质心点是唯一性的,不随车辆行车姿态而变化;工作姿态下,天线的质心点随天线的运动发生变化,天线车的稳定性计算变得复杂。

图1 空间力系示意图
重型天线车一般由牵引车、半挂车、平台总成、平台附件、天线等组成。依据空间任意力系的普遍规律,可以推导出天线车两种姿态下失稳临界点的力系平衡方程。为简化表达,在公式中依次用数字1、2、3、4、5代替天线车各组成。
以天线车失稳着力点为原点建立坐标系,其中重力轴为Y轴(反方向为正),天线车身纵向为X轴(运行反方向为正),Z轴依据右手坐标系规则确定。
运输姿态下天线车因路况坡度变化,重力在各轴的分力不同,处于临界失稳条件下的力系平衡方程表示如下:
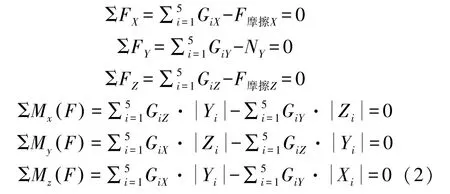
式中,G为重力;X、Y、Z为重力作用至各轴的力臂。
2月16日,国家防汛抗旱总指挥部正式批复《韩江洪水调度方案》,要求珠江防汛抗旱总指挥部和福建、广东两省防汛抗旱指挥部门,认真落实方案中确定的各项任务和措施,做好韩江洪水调度工作,确保韩江流域防洪安全。
工作姿态下牵引车脱开,平台总成处于水平姿态,重力沿Y轴垂直向下,没有另外两个轴的分力,重力作用在Y轴上的力矩为零。天线重力作用于X和Z轴的力矩随方位运动而变化,将天线电轴的水平分量与X轴的夹角α作为变量,推导出工作姿态天线车处于临界失稳条件下的力学方程:
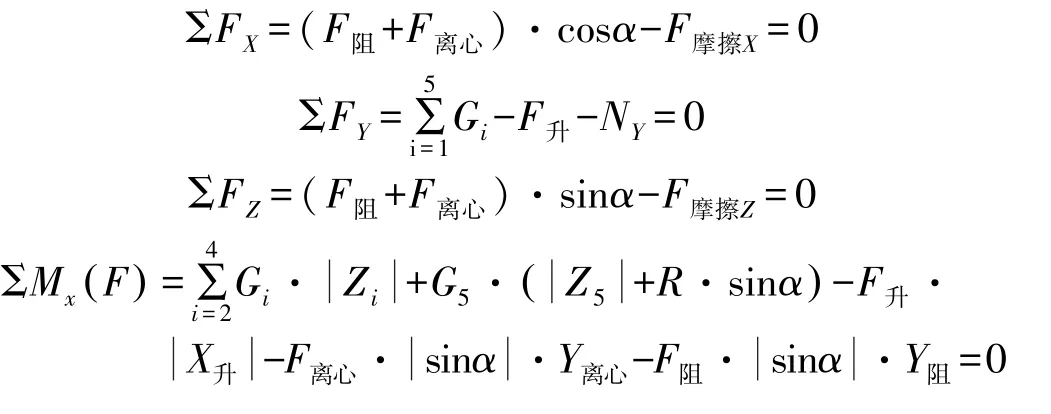
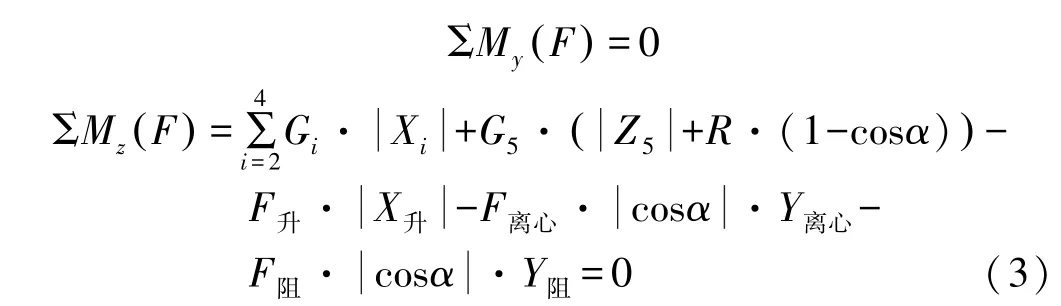
式中,F阻和F升为天线车受风引起的载荷,可由仿真或风洞试验获得;F离心为运动部位离开中心的力;R为天线重心绕方位轴旋转时的力臂。
3 设计计算
3.1 实例分析
某重载型相控阵天线车因天线体量较大,超出普通机动式载车的承载上限,选择重载型牵引车和半挂车作为运输载体。为适应机动性需求,该天线可自动完成折叠展收以及平台总成的架设和撤收,快速实现工作姿态和运输姿态间的转换。工作姿态下,天线可在35 m/s风速下不破坏,天线360°方位旋转,方位速度最大为36°/s,仰角60°~80°可调,仰角调节完毕后固定,方位旋转时俯仰角度不变。
该重载型相控阵天线车由牵引车、半挂车、平台总成、平台附件、天线组成,其运输姿态和工作姿态下各组成的部分的姿态见图2和图3。该重载型相控阵天线车完成其使用性布局设计后,以降低重心高度、控制偏载为准则完成功能性布局,反复校核机动性及稳定性,直至满足使用要求。本实例从运输姿态和工作姿态两种情况进行稳定性计算。

图2 某重载型相控阵天线车运输姿态组成图
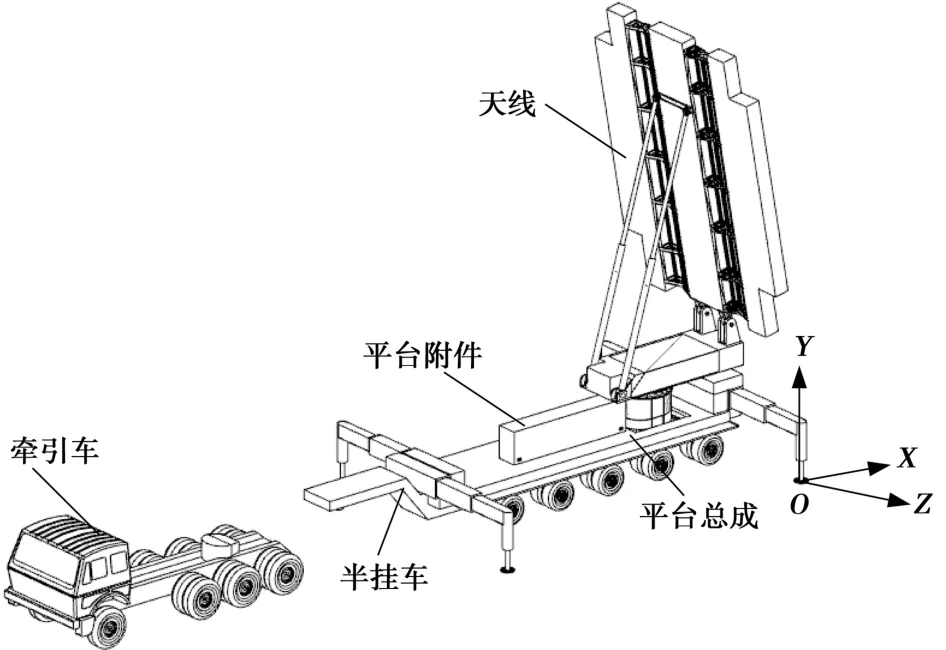
图3 某重载型相控阵天线车工作姿态组成图
3.2 运输姿态稳定性计算
重载型相控阵天线车运输姿态下,在纵坡行车、纵坡停车、侧坡行车和侧坡停车4种条件下存在失稳风险。本实例以方程(2)为理论基础,分别对4种条件进行计算分析。
(1)纵向最大行车坡度α
以上坡为例,天线车在纵坡上行驶时,当前轮受力为0,车辆处于纵翻的临界点,此时的纵向坡度为纵向最大行车坡度。运用天线车运输姿态下失稳临界力系平衡方程(2)中绕Z轴力矩平衡方程可得纵向最大行车坡度:
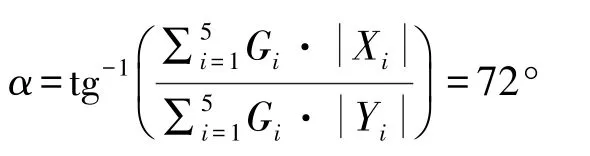

图4 纵坡上行示意图
(2)侧向最大行车坡度γ
天线车在侧坡上行驶时,当左轮受力为0,车辆处于侧翻的临界点,此时的侧向坡度为侧向最大行车坡度。运用天线车运输姿态下失稳临界力系平衡方程(2)中绕X轴力矩平衡方程,可得纵向最大行车坡度:
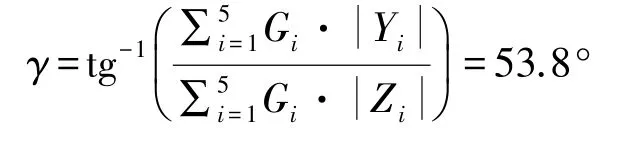
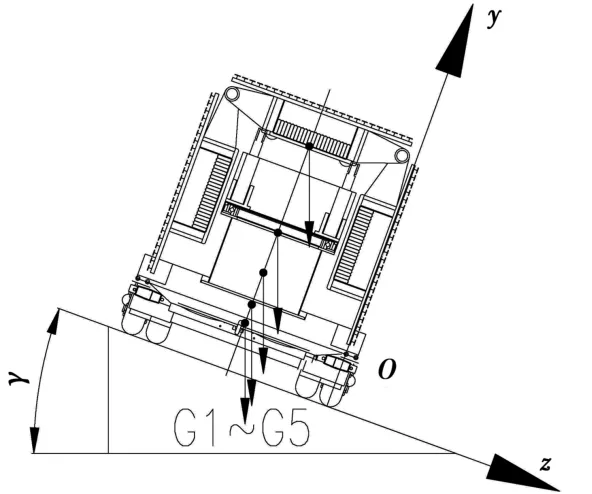
图5 侧坡行驶示意图
(3)纵向最大停车坡度β、侧向最大停车坡度θ
天线车在纵坡或侧坡驻车时,不发生滑动的前提条件是整车的摩擦力F摩擦大于重力沿斜坡的分量,运用天线车运输姿态下失稳临界力系平衡方程(2)中沿X轴或Z轴力平衡方程,可得出下式:

式中,μs为静摩擦系数,干燥的沥青或混凝土路面一般取0.75[4],雨天路面静摩擦系数为0.5~0.75,可采取抛洒碎石等措施获取较高的静摩擦系数。
3.3 工作姿态下稳定性计算
天线车工作姿态下,半挂车与牵引车脱开,半挂车在4条主力支撑腿的助力下将天线车的载荷经支撑腿、垫木传递至地面,保持天线车的工作稳定性。天线车工作姿态下应排除滑移和倾翻两种失稳风险,本实例以方程(3)为理论基础分别对其进行计算分析。
(1)滑移
天线车在工作姿态不发生纵向滑动的前提条件是:整车的摩擦力F摩擦X大于X轴的分力,运用天线车工作姿态下失稳临界力系平衡方程(3)中沿X轴力平衡方程:
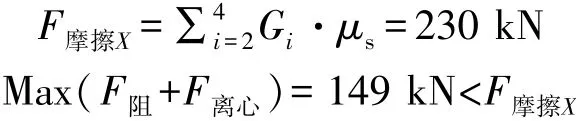
式中μs为静摩擦系数,软木与地面的静摩擦系数为0.6,软木⁃铸铁的静摩擦系数一般取值0.3~0.5[5],滑移发生在天线车支腿与软木接触面上,本文μs取0.4。
由计算可知,该重载型相控阵天线车工作姿态下不会发生滑移现象。
(2)抗倾翻
天线车工作姿态(见图6)下,倾翻的临界点为因受风阻力、升力和离心力的共同作用,某一支撑腿受力为0。因α角度周期变动影响,运用数据分析和处理,可得出α为270°即天线重心靠近坐标原点时外力的相对影响最大,可用下面的绕X轴的力矩平衡方程分析天线车是否倾翻失稳:
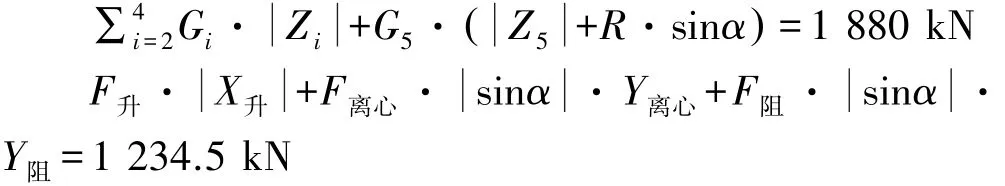
因风阻力、升力和离心力的作用力矩小于重力矩,可知该天线车不会因外力倾翻。

图6 工作姿态示意图
4 仿真校核
运用NX10建模,在“运动仿真”模块内建立运动副,并施加相应载荷,得出各姿态下的时间⁃位移图形,如图7~11所示。在临界角度上,运输姿态在重力载荷作用下,工作姿态在重力和外力载荷作用下,位移为零,未发生滑移或倾翻失稳情况。
通过运动仿真手段模拟本文实例中各临界姿态,验证了计算的正确性。
图7 72°纵坡抗倾翻仿真
图8 36.9°纵坡驻车制动仿真
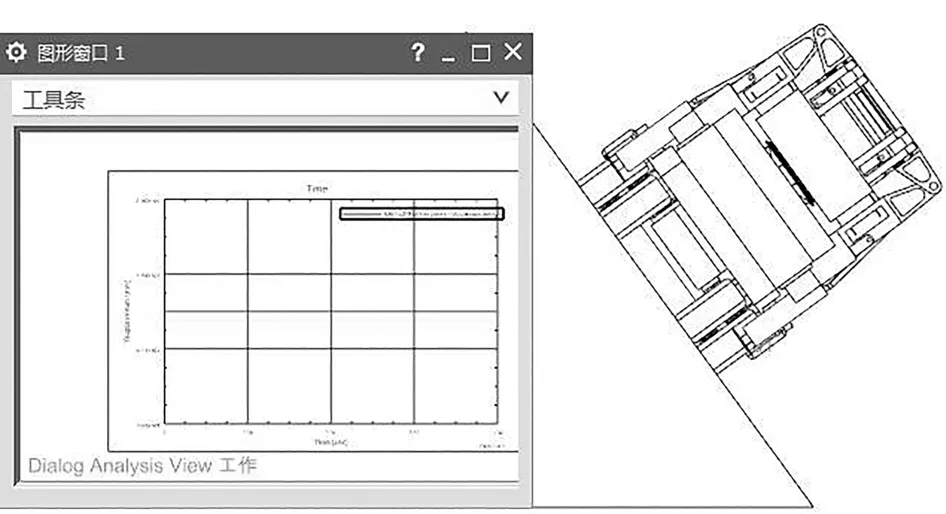
图9 53.8°横坡抗倾翻仿真

图10 36.9°横坡驻车制动仿真
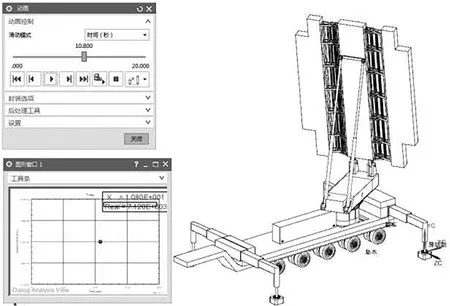
图11 工作姿态运动仿真
5 结束语
本文依托空间力系平衡理论,推导了一种适用于改装车辆稳定性计算的方法。通过计算某重载型相控阵天线车稳定性,并将计算结果作为仿真模型的边界条件,经仿真验证了该方法的合理性。在机动型雷达方案设计时,通过该方法计算天线车的稳定性,可合理配置重心,避免重复修改结构模型,有效减省设计时间,提前释放设计风险。

