一种网络中心战数据传输效率度量方法

肖 鹏，王 岩，于海霞

（空军航空大学 航空作战勤务学院，长春130022）

0 引 言

网络中心战（Network Centric Warfare，NCW）是由平台中心战逐步发展而来的综合一体化打击系统，并集成了全局信息网络、传感器网络和投射器网络。美国海军研究生院的Phillip E.Pace教授对NCW的定义为：在现有传感器信息与网络技术水平条件下，将分散的决策制定人员、武器系统、态势与瞄准传感器和部队广泛地集结在一起，使之成为一个高度自适应的综合军事行为系统，以获得前所未有的作战效能。［1］

NCW并不是简单地将若干种类型的传感器人为地拼接到一起，其为了追求作战效能的最大化，在根据不同的作战任务和环境因素等综合作战需求的前提下，如何最大限度地发挥每个网络节点的效能才是NCW的核心所在。［2⁃3］如果让网络拓扑结构肆意扩大，不仅会给网络信息态势共享带来困难，还会打破节点间协同处理的优势，这对整个NCW来说是灾难性的。为了体现这种作战优势和缜密的战斗序列部署能力，从图1着手对NCW的工作流程进行分析。

传感器网络在空间探测到目标后将态势信息共享到决策和投射器节点，决策系统在整个NCW中占有最高优先权［4］，负责NCW的任务规划和资源调度。决策系统控制投射网络对目标实施跟踪定位，并根据目标的移动轨迹及投射器的战术技术指标对传感器共享的态势信息进行修正，最终将毁伤效果通过传感器网络反馈到决策中心。

通过对典型NCW系统工作流程的描述发现，这种定量的描述语言过于笼统，很难对NCW系统有一个深入分析的切入点。利用接下来的数学模型，可以全面剖析NCW网络拓扑结构的优越性。

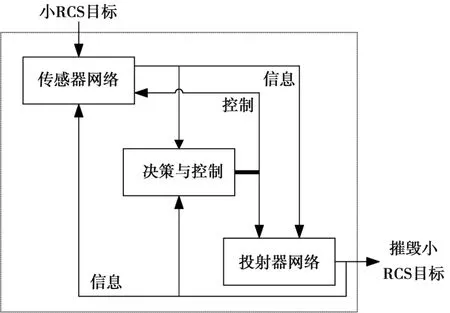
图1 典型NCW系统组成及工作流程

1 广义连接性量度

在以多传感器和武器为平台的作战体系架构中，一个与时间t相关联的广义连接性量度CM被定义为［5］

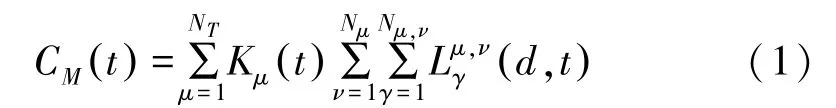
其中，NT表示网络中的节点数目；Nμ是连接到节点μ的所有节点数目；Nμ，ν表示连接节点μ和γ的所有可能路径的数量总和；是节点的能力值，根据节点在网络拓扑中担负的任务不同，Kμ(t)值也不尽相同；是连接节点μ和ν的路线γ的信息流参数，是路径长度d和时间t的函数。

为了简化与路径d以及时间t的函数关系，将分为时间无关量Lμ，ν和时间相关量(t)，且(t)正比于d的ξ次幂。于是式（1）可以简化为

若再考虑一种理想的网络连接状态：假设Kμ(t)是时间无关的，且拓扑结构中的任意两个节点要么是相连的，要么是不相连的（或为1）；对所有路径d，标度量指数ξ＝1，时间无关信息流量参数Lμ，ν＝1。则式（2）可以进一步简化为

由式（3）可以归纳出：连接性与时间无关，即Kμ(t)＝Kμ和其任意两个节点要么是相连的，要么是不相连的。

2 参考连接性量度

参考连接性量度被定义为一个所有网络节点全部双向互联的拓扑结构，且每一个节点的能力值Kμ＝1，参考连接性量度只与节点总数相关：

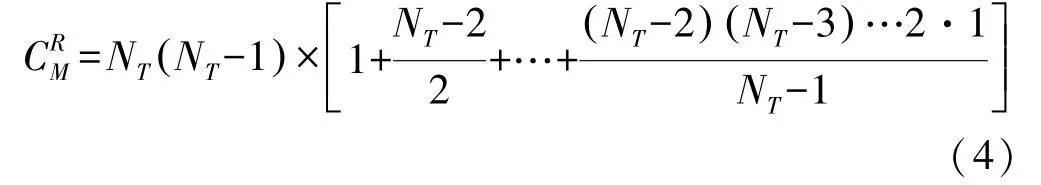
由此可以看出，对于节点数目相同的网络拓扑结构，参考网络具有最高的连接性量度。

3 网络覆盖率

当用对式（3）进行归一化处理时，就得到了网络覆盖率IR的定义：

利用参考网络归一化可以研究网络连接、不同节点（连接）的变化程度。在网络节点发生故障或遭到网络电子攻击时，IR可以全面统计分析这种不利因素对网络性能造成的破坏效果，从而在确保NCW不丢失基本作战效能的前提下，使整体作战效能最大化，并为指挥人员谋划新的作战策略提供支撑。

4 扩展广义连接性量度

当某条路径上一个被横穿节点的能力值较低时，此路径将很难维持全面的传感器信息交互能力。这不仅严重阻碍了该条路径上所有节点效能的发挥，还成为制约整个拓扑网络信息畅通交互的隐性因素。为了彻底排除这种潜在的不利因素，现将关于连接性量度的定义扩展如下：

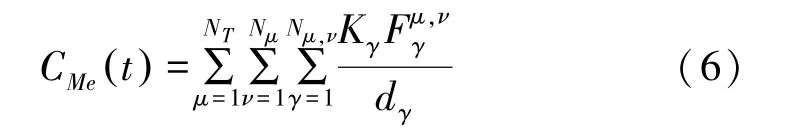
其中，Kγ表示路径γ的最低能力权值Kμ，且Kγ值的选取仅考虑开始节点与交换节点，这是因为许多军事网络的节点只接收数据，而在发射时无等效的信息处理能力。

5 网络中心战联合打击场景模拟

考虑一种场景设置：从“查菲”号驱逐舰（能力值K＝1.0）发射一枚“战斧”式巡航导弹，以摧毁某个恐怖组织的武器系统，如图2所示。为追踪得到摧毁效果报告，一架“捕食者”无人机紧跟着“战斧”式巡航导弹。为了提供情报、监视和侦察能力，还使用了一架“全球鹰”无人机（K＝0.8）。“战斧”式巡航导弹的能力值假定为K＝0.3，这是出于其有限的连接性和信号路由变更的选择（它到“全球鹰”是单向连接），“捕食者”也只有有限的信号路由变更能力，并假定能力值K＝0.5。考虑到每条连接有一个流通量，其值要么是1，要么是0。

图2 NCW作战场景模拟

为了定量分析此次打击行动的NCW作战效能，结合上述分析指标并利用MATLAB构建了图3所示的系统仿真链路图，其中细线代表NCW系统中网络拓扑节点间的连接关系，粗线代表NCW即将攻击的目标链路。最终计算结果如表1所示。

表1中，CM＝10.3333，IR＝0.32。表1分析了图3中每条可能存在的链路的连接情况，并指出了每条链路的贡献值和瓶颈节点，其中第3、12、23、26、27、30号链路对整个网络的贡献值最低（同为0.1），且这几条链路的瓶颈节点同为4号节点（“战斧”式巡航导弹的能力值假定为K＝0.3），这与场景建立过程中的预设条件吻合，说明了这种度量方法的准确性和可行性。为了更全面地分析度量方法的可行性，在下面的场景模拟中，假设将“捕食者”无人机从NCW系统中去除掉，则构建的仿真链路模型如图4所示，计算结果如表2所示。

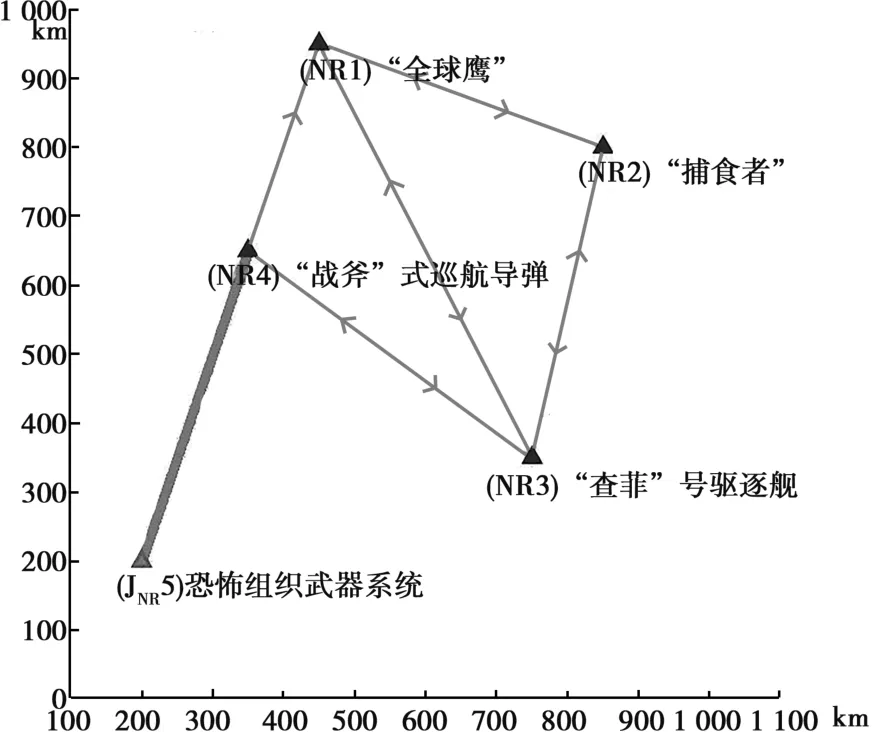
图3 系统仿真链路图

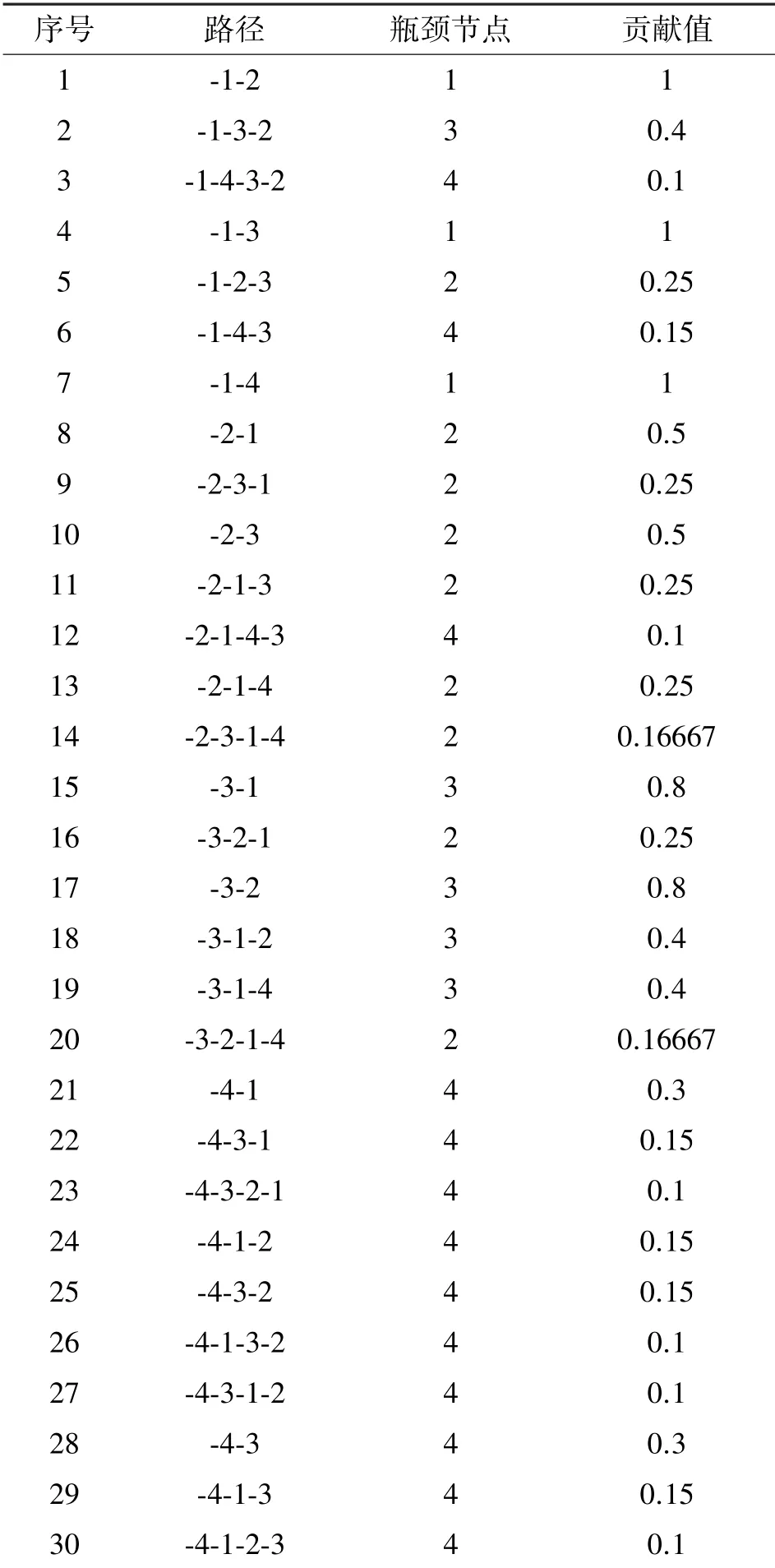
表1 扩展连接性量度计算结果

图4 去除“捕食者”无人机后的仿真链路图

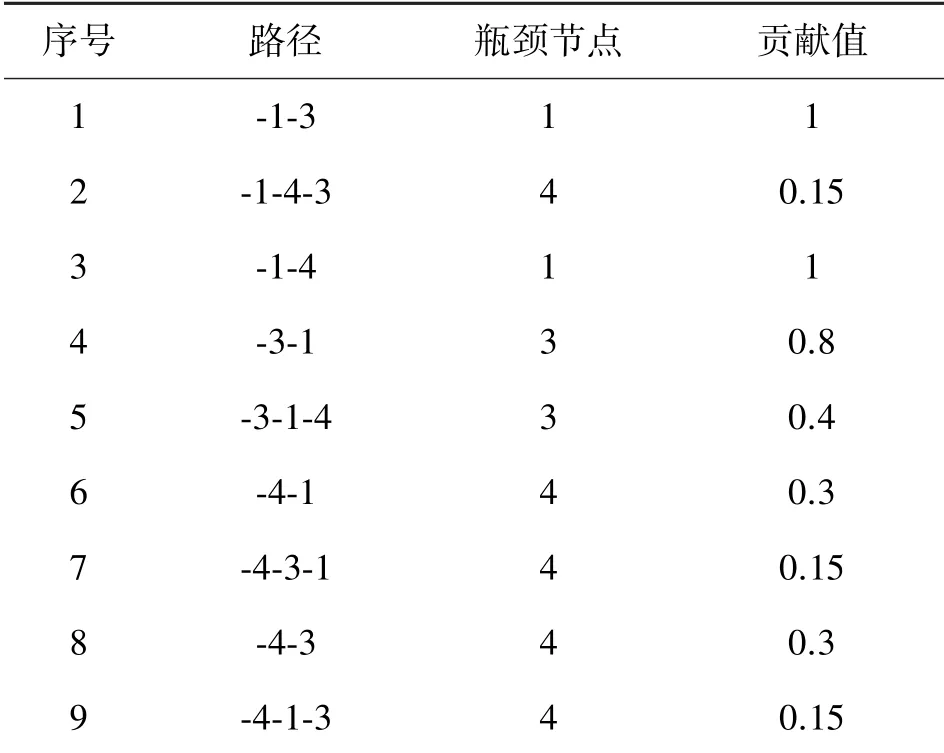
表2 去除“捕食者”无人机的扩展连接性量度计算结果

表2中，CM＝4.25，IR＝0.47。对比表1发现，表2中去除“捕食者”无人机后网络连接性量度下降的同时，网络的覆盖率反而增大了。这是因为图4的NCW在缺少战场毁伤跟踪这一角色后（在图3中由“捕食者”无人机承担），“全球鹰”节点的数据流通量明显增大了，在发挥“全球鹰”潜在能力的同时整个网络的作战效能比图3所示的NCW提升了46.9%。这与“如何最大限度地发挥每个网络节点的效能才是NCW的核心”的思想是相符的，再一次证明了这种度量方法的可行性。

6 结束语

通过获得NCW的连接性量度和网络覆盖率，可以全面分析网络的鲁棒性；通过这些数值的比较，使受到攻击时的实际网络行为现象表现出来。实际上，连通测试量值的变化速率是断开连接和受到攻击节点的数目的函数，为观察传感器网络的鲁棒性提供了一个很好的手段。

随着网络拓扑节点数目的增加，网络复杂性和稳健性逐步提升，节点间的协同响应变得复杂，同时节点对整个网络结构的贡献值变得微弱。为了获得更高效的协同作战体系结构，从本文的仿真结果来看，应尽量减少网络节点的数量，努力将信息优势转化为打击优势，最大限度地展现出网络中心战的作战效能。