3D打印送粉颗粒温度场研究
厉鸿韬,黄延禄,邓鸿信,陈致伊,胡安锴
(华南理工大学 机械与汽车工程学院,广东 广州 510641)
定向能量沉积技术(Directed Energy Deposition, DED)是3D打印的一种典型方法,它利用激光或其他高能束加热粉末颗粒或焊丝至熔化然后冷却并凝固,形成沉积层[1-2],它具有众多优点:1)拥有较快的沉积速率,加工效率高;2)可以通过逐行沉积金属材料在平坦或不平坦的基板上成型任意形状的工件;3)DED设备的系统简洁,因此很容易开发出将DED与不同制造工艺相结合的混合工艺;4)DED系统可以通过连续同时沉积不同的材料来轻松制造具有所需性能的非均匀材料工件[3]。鉴于上述优势[4],近些年来,DED工艺的研究和应用稳步增长。刘昊等[5]针对送粉式定向能量沉积过程中瞬态温度场和熔覆层几何形貌建立了三维数值模型,分析了熔覆过程中的温度场变化和几何形貌特点。李俐群等[6]对超高速定向能量沉积进行了研究,所研究的超高速熔覆技术形成的涂层稀释率更低,拥有更加细致的整体组织,并且具有更优异的耐腐蚀性能。AeroMet公司使用激光成型法通过粉末生产航空航天所需要用到的钛合金零件,降低了生产成本[7]。
DED技术可以通过旁轴送粉和同轴送粉2种方式将粉末输送至熔池中。送粉喷头是实现定向能量沉积技术的重要零部件,其结构决定了粉末的聚焦性能和粉斑尺寸。王方等[8]设计了一种装有倾角显示仪器和同轴引导光的旁轴送粉设备,可以快速引导激光与粉末重合,从而提高粉末利用率。在喷头送出粉末后,激光束与粉末流的相互作用对于工件成型质量也有较大影响。杨永强等[9]通过有限差分法建立了激光束对粉末颗粒的升温模型,计算了不同材料、颗粒粒径以及激光功率情况下粉末颗粒的温度变化曲线。Huang等[10]通过经典光学理论建立了激光束与粉末流相互作用的模型,研究表明当送粉速率增加时,加工基板表面的激光强度以及粉末颗粒温度峰值都会下降。上述多位学者所设计的不同送粉喷头,所输送的粉末颗粒分布存在一定的差异。而目前激光束与粉末颗粒的相互作用模型中,对于粉末颗粒分布较多是采用高斯分布的方法进行计算,这样未必能够显示出不同送粉喷头的送粉特性。
按一定比例从粉末颗粒分布中提取一定数量的颗粒,这些颗粒可以代表整体的粉末颗粒分布。本文基于粉末颗粒具体位置分布,建立了激光束与粉末流相互作用模型,分析了同轴送粉和旁轴送粉2种不同送粉方式下粉末颗粒的温度分布。
1 粉末流浓度分布
本文所用到的新型送粉喷头送粉示意图如图1所示。图1a为同轴送粉示意图,激光束和粉末颗粒同时进入送粉喷头中,粉末颗粒在送粉喷头中逐渐汇聚形成一道粉末流,继而逐渐收缩;图1b为旁轴送粉示意图,右侧的新型送粉喷头结构代替了传统逐渐收窄形状的粉末通道结构进行送粉。

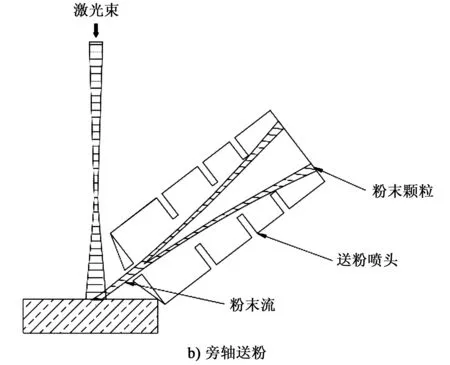
图1 喷头送粉示意图
该种新型送粉喷头与传统送粉喷头在送粉效果上存在一定的差异,通过Fluent软件模拟计算其粉末运动轨迹(见图2),显示了粉末颗粒离开送粉喷头20 mm范围内在xoy平面上的分布。从图2中可以发现,粉末颗粒离开送粉喷头后呈现出逐渐汇聚的状态。

图2 送粉喷头出口20 mm内粉末颗粒分布
粉末颗粒在喷头出口不同位置处yoz平面上的分布如图3所示。图3a和图3b分别为粉末颗粒在距离送粉喷头出口10和20 mm处的分布效果图。可以看出,随着粉末颗粒至喷头距离增加到20 mm,颗粒在yoz平面上的分布半径逐渐变小。
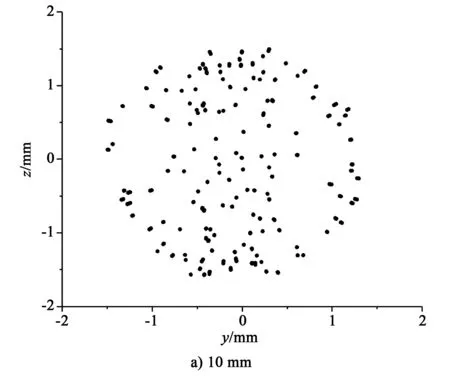
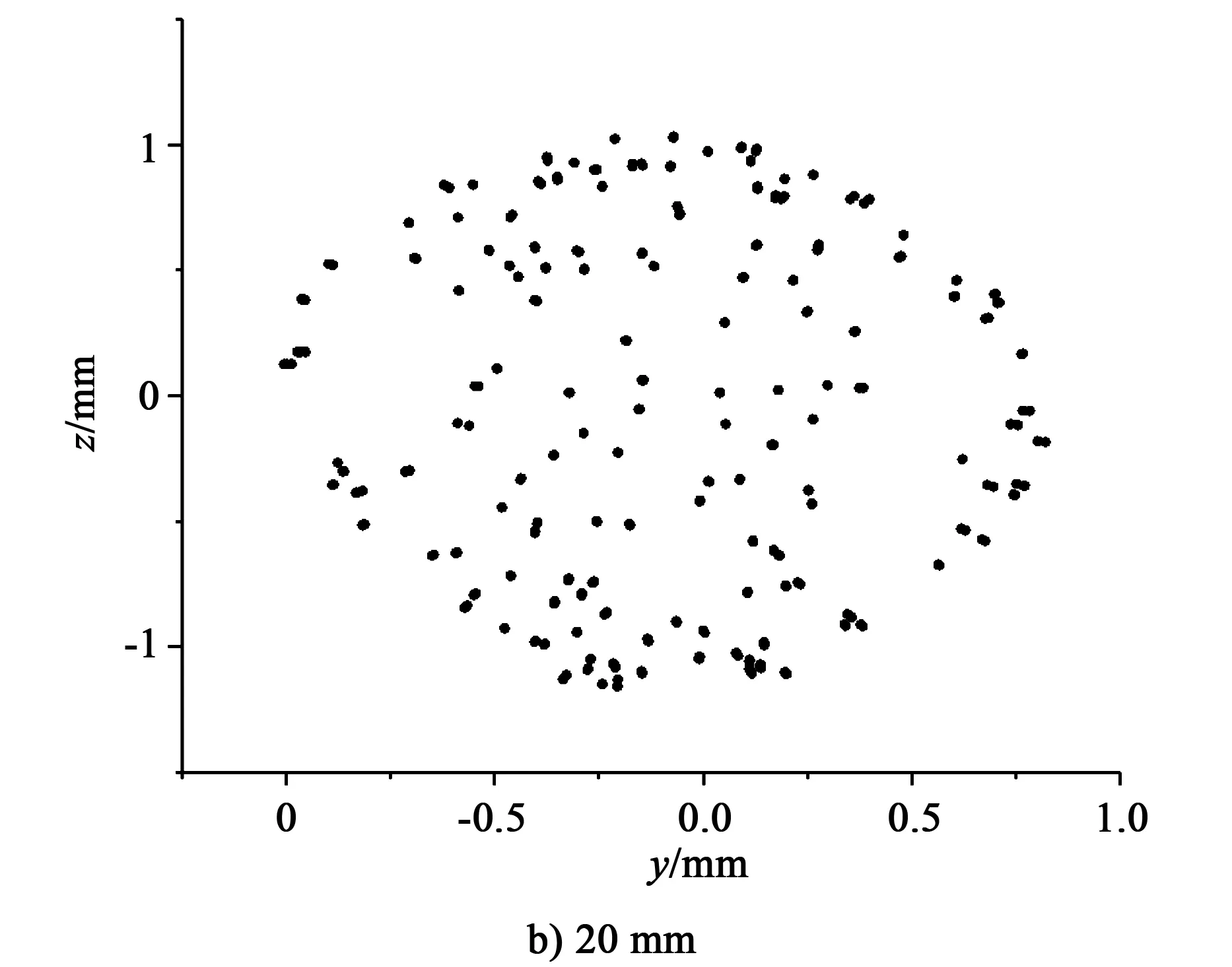
图3 粉末颗粒在喷头出口不同位置处yoz平面上的分布
2 激光束对粉末颗粒的照射升温
2.1 激光束对粉末流的照射升温模型
粉末颗粒在运动过程中会与激光束相遇,粉末流的运动轨迹,以及激光束的能量强度,都会对粉末颗粒的温度产生影响。尤其是在图1a所示的同轴送粉过程中,粉末流会在激光束中运动较长一段距离,温度变化对粉末颗粒影响较大,因此必须对粉末颗粒的温度进行研究,才能确定粉末颗粒进入熔池前的状态以及温度分布。
粉末流与激光汇聚示意图如图4所示。坐标原点O为激光斑点的中心,粉末流基本为收缩的圆锥形,其轴线与水平方向成一倾角I,即送粉角度。当I=90°时,粉末流和激光束的轴线重合,即同轴送粉;当时,粉末流从一侧进入激光束中,即旁轴送粉。坐标原点O与送粉喷嘴的距离为d,d取10~20 mm均可用作加工距离。可以调整送粉速率、送粉角度I和送粉距离d以达到最佳的工艺参数。
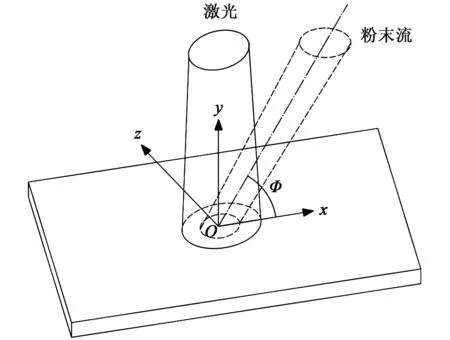
图4 粉末流与激光汇聚示意图
首先对粉末流的有效半径R进行计算,需要注意的是,当粉末流和激光束同轴时,粉末流截面有效半径R为粉末流水平截面的半径;当粉末流侧向送粉,即φ<90°时,粉末流截面为粉末流平行于xoz平面所取的截面,粉末流有效截面的计算式可分为如下几个阶段。
1)当所有粉末颗粒在激光束外,即r>R1时(为激光束半径),激光束无法照射到粉末流,此时粉末流截面有效半径R(x0,y0,z0)=0。
2)当有粉末颗粒进入激光束内,但并非所有粉末流都处于激光束内时,R的表达式为:
422 Senescence-associated secretory phenotype and its complex regulation networks: a review of molecular mechanisms
(1)
式中,坐标(xi,yi,zi)为该层粉末流截面内某颗粒的三维坐标,i=1~n,n为该层粉末流截面内所有距离激光束轴线r≤Ri的粉末颗粒。
3)当所有粉末颗粒进入激光束内(xoz平面内),R的表达式为:
(2)
当确定了送粉角度φ和送粉距离d,那么在喷嘴出口到加工基板这段距离内,粉末流的颗粒浓度分布相对来说就是固定的,通过确定送粉速率、粉末颗粒运动速度、颗粒密度和颗粒尺寸即可计算出这段距离内,以-y为方向的单位长度Δy粉末流内粉末颗粒的总数Nt:
(3)
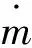
通过对送粉喷嘴出口20 mm范围内颗粒位置数据的分析计算,结合式1~式3,可以写出粉末流内任意一点(x0,y0,z0)处单位体积内粉末颗粒的数量为:
(4)
对激光能量的计算方式可通过如下方式计算得到,激光束在穿过粉末前的激光强l0(x,y,z)度符合高斯分布:
(5)
(6)
根据Lambert-Beer定理,激光束从粉末流中穿过时,激光强度不断衰减,呈现出指数衰减规律:
(7)
式中,激光强度l(x,y,z)是激光束在l0(x,y,z)的初始激光强度条件下,穿过距离为L的粉末流后的透射激光强度;Kp是粉末颗粒的消光系数;l是与粉末流中位置(x,y,z)相关的函数。消光系数Kp由下式表达:
(8)
式中,a=(2πRp)/λ,本文所使用的粉末颗粒平均半径为20 μm,激光波长为10.6 μm,可以计算得到a的值为14.82,算出消光系数Kp=2。
粉末颗粒在激光束中受到照射而导致温度的上升可由下式进行计算:
(9)
式中,等式左端为粉末颗粒从激光束中穿过时,每向下运动一个空间步长Δy所净吸收的能量;cp是颗粒材料的比热容;ΔT是经过一个空间步长Δy颗粒上升的温度;Qp是粉末颗粒从激光束中吸收能量后减去由对流散热和辐射导致的热损失所剩余的能量,可通过下式计算得到:
(10)
式中,l(x,y,z)是某颗粒所处位置(x,y,z)处的激光强度;ap是粉末颗粒的激光吸收率;σ是辐射常数;εp是粉末颗粒的黑度系数;Tf是外界环境温度;T是该粉末在(x,y,z)位置处的温度。
2.2 粉末颗粒温度的计算结果
利用上述计算模型对颗粒温度进行计算,本文以316L粉末颗粒为例进行计算,计算过程中用到的相关参数见表1。

表1 计算中所用到的工艺参数和粉末颗粒材料物性参数
首先对该粉末分布条件下的同轴送粉进行计算,送粉速率为0.9 g/s。图5所示为粉末颗粒在送粉喷头不同位置处熔化占比,从图5中可以发现,随着粉末颗粒在送粉喷头中不断运动,越来越多的粉末颗粒开始熔化,最多时有27%的粉末颗粒被熔化了。观察图5可以发现,当距离>50 mm时,逐渐有粉末颗粒开始熔化,因此在图1a的同轴送粉方式下,送粉喷头的长度应<50 mm,否则会有粉末颗粒在送粉喷头中熔化。
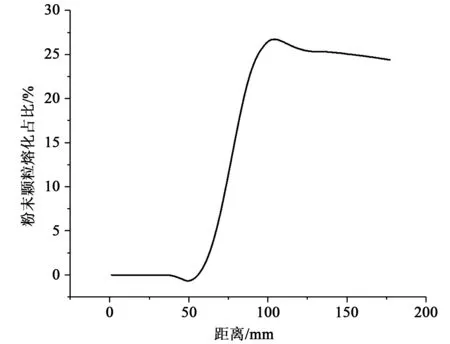
图5 粉末颗粒在送粉喷头不同位置处熔化占比
下述对旁轴送粉时粉末颗粒温度进行计算,计算过程中用到的相关参数见表1。将激光功率提升至2 800 W,对不同送粉角度和不同送粉速率的条件分别进行计算,计算结果如图6所示。
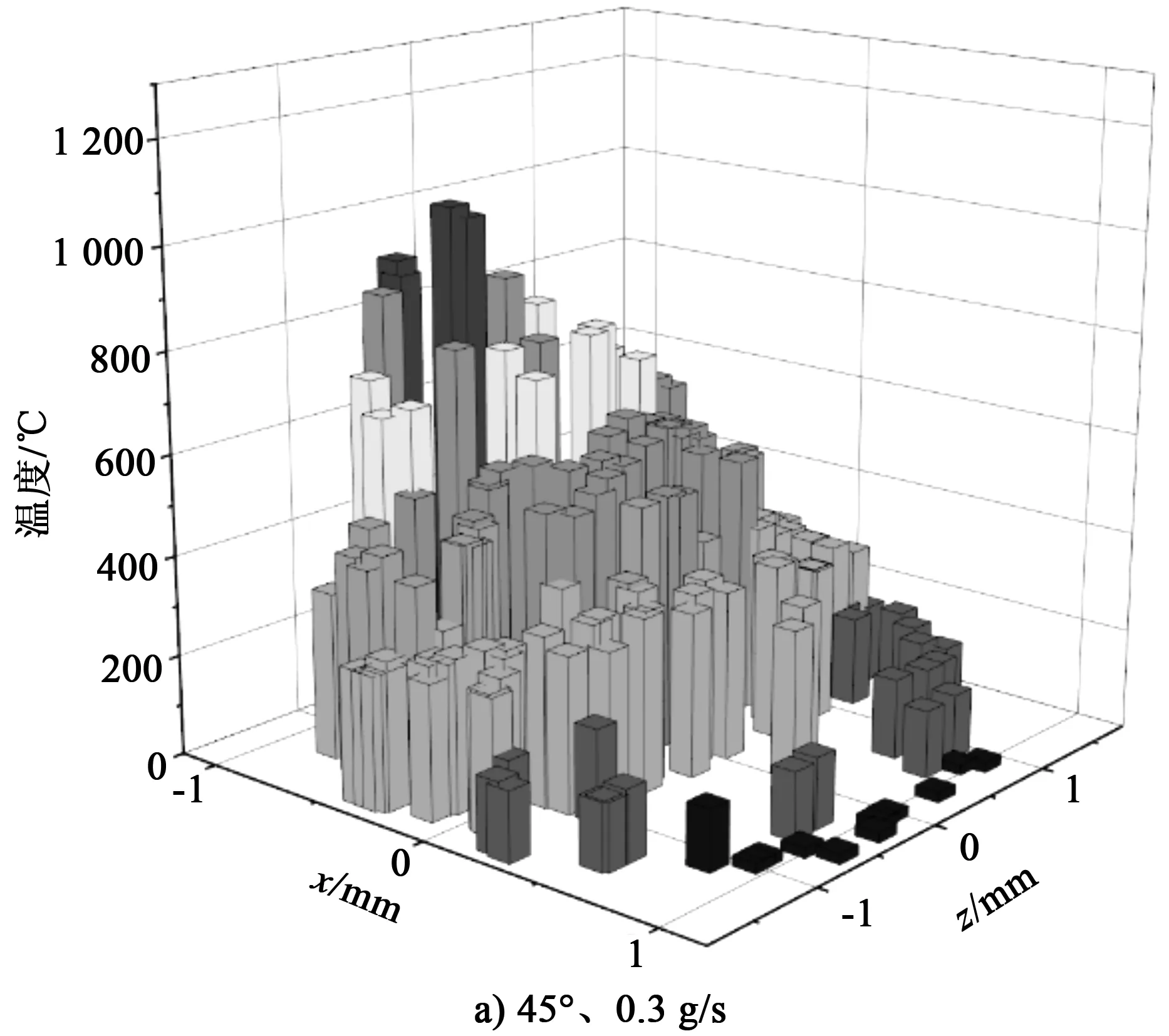
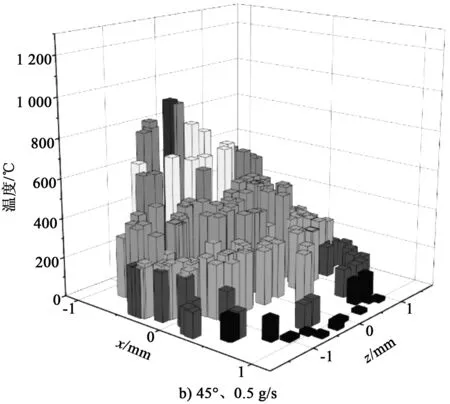
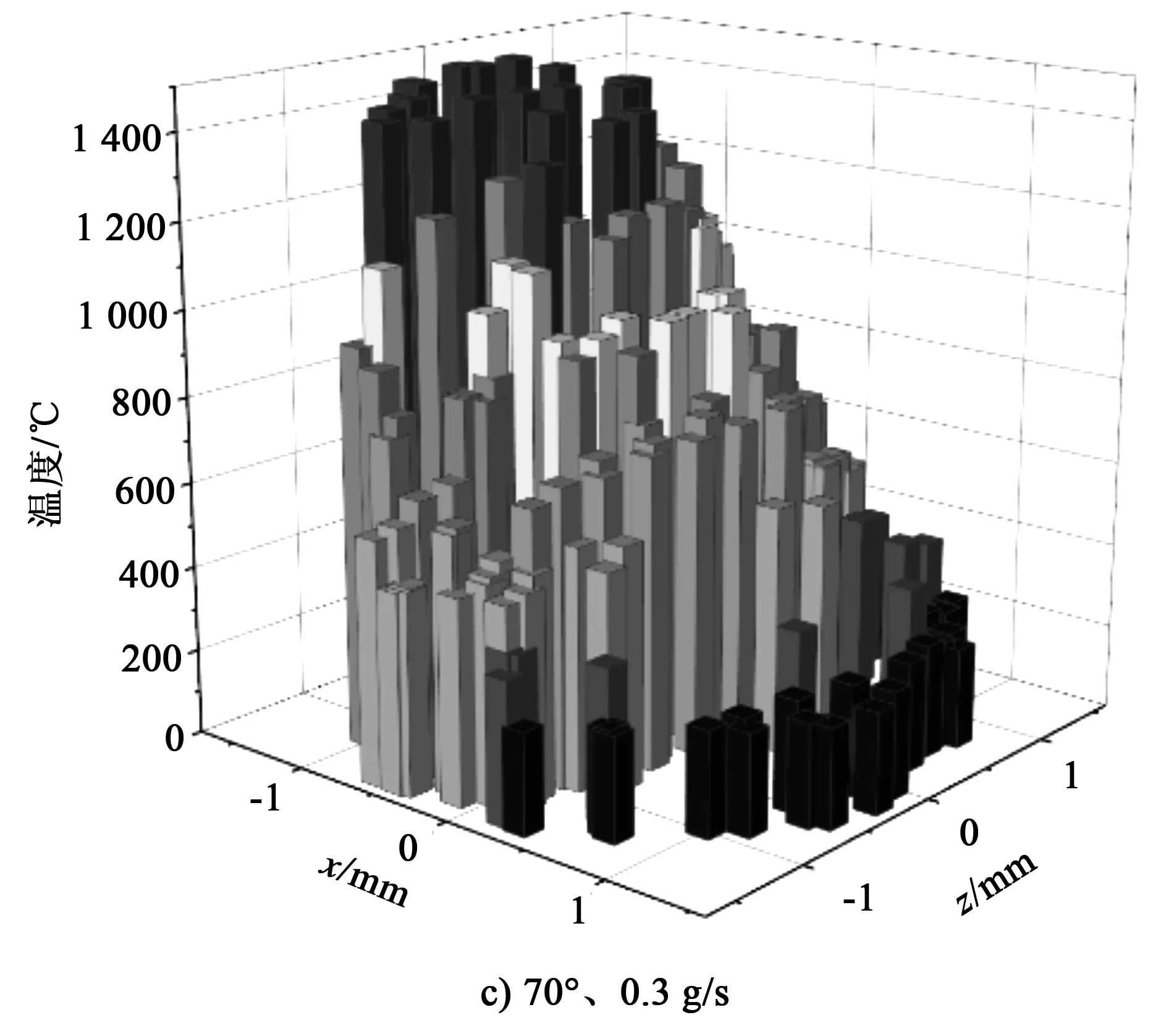
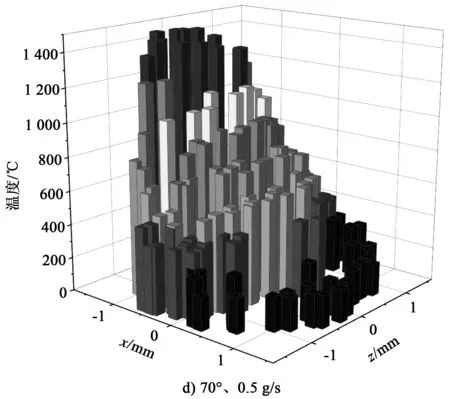
图6 旁轴送粉时粉末颗粒温度分布
图6a为送粉速率为0.3 g/s、送粉角度为45°条件下粉末颗粒的温度分布。可以发现,越靠近z轴中心,x轴负边界,颗粒温度越高,这是因为粉末颗粒从x轴的正方向逐渐穿过激光束(见图4),最终落在了加工表面的左侧。图中最左侧的颗粒在激光束中受到照射时间最长,且处于z轴中心的颗粒经过了激光束中激光强度最高的区域,因此会呈现出从左往右温度逐渐降低的趋势。图6b为送粉速率为0.5 g/s、送粉角度为45°条件下粉末颗粒的温度分布。对比图6a可以发现,粉末颗粒的温度略有降低,这是因为当粉末流浓度上升后,增强了对激光束能量的削减,同时粉末颗粒受到的激光照射强度也降低了。图6c为粉末颗粒在送粉速率为0.3 g/s、送粉角度为70°条件下到达加工基板时的位置和温度分布,与图6a对比可以发现,整体的颗粒温度都上升了不少,这是因为当送粉角度增大时,粉末流更早地进入激光束,导致粉末颗粒温度整体上升。图6a中左侧最高温度的颗粒温差较为明显,而6c中左侧的颗粒温度差距并不明显,通过观察颗粒温度已经达到1 400 ℃以上,达到甚至超过了颗粒材料的熔点,因此熔化潜热吸收了较多的能量,用来作用颗粒温度上升的能量反而较少,这也就导致了粉末颗粒在左侧最高温度的分布较为均匀,这一点在图6d中也有显现。由此可以发现,当送粉角度为70°时,粉末颗粒整体温度高,部分颗粒在进入熔池前开始熔化,这样有利于形成较少颗粒的反弹。
3 结语
通过上述研究可以得出如下结论。
1)建立了基于粉末颗粒具体位置分布的激光束与粉末流相互作用的模型,考虑了粉末流对激光束能量的削减作用,以及颗粒升温时对周围环境的辐射换热和对流换热损失的热量,对于计算此类问题具有适用性。
2)对同轴送粉和旁轴送粉喷头所输送的粉末颗粒进行了温度计算,同轴送粉时粉末颗粒升温迅速,需要缩短喷头长度以避免颗粒在喷头中熔化。旁轴送粉时,增大送粉速率会导致粉末颗粒温度下降,增大送粉角度会导致粉末颗粒温度上升。

