基于ANSYS Workbench的扭转弹簧疲劳寿命分析

时宏森，杨 涛，唐 超，蔡大静，陈 强

(1.贵州航天林泉电机有限公司，贵州 贵阳 550081；2.国家精密微特电机工程技术研究中心，贵州 贵阳 550081)

疲劳寿命试验是一项耗时、耗资的大型试验，时间周期长、子样数量大、数据处理复杂是疲劳寿命试验的主要特点，对机械产品的每一个零件都开展疲劳寿命试验显然是不现实的。根据材料疲劳理论，结合电子计算机及有限元技术的发展，可以通过虚拟仿真试验确定产品零件的疲劳寿命。

弹簧的工作寿命一般在104～105以上，一般来说属于长寿命机械零件，失效模式属于高周疲劳[1]。本文应用ANSYS Workbench软件首先对某扭转弹簧进行强度仿真，得到使用工况下的应力、应变分布结果及应力梯度变化数据，然后应用ANSYS Workbench软件自带的疲劳分析模块，对扭转弹簧的疲劳寿命进行计算分析。同时，结合扭转弹簧实物试验，获得产品真实的疲劳寿命，对仿真计算结果进行修正，从而形成一套实用的疲劳寿命理论计算方法。

1 材料数据

1.1 材料拉伸数据

扭转弹簧材料为60Si2Mn[2-3]，材料弹性模量E为210 GPa，泊松比μ为0.29，屈服强度σ0.2为1 505 MPa,强度极限σb为1 719 MPa。

弹塑性计算用双线性模型，弹塑性数据的切线模量取1 450 MPa，在理想弹塑性下切线模量取0 MPa。

切线模量EG拟合用公式

式中，φ是断面收缩率；δ5是延伸率。

1.2 材料疲劳数据

疲劳计算采用应变-寿命方程，考虑平均应力修正的Morrow方程[4-5]：

材料受循环载荷时，循环应力-应变方程：

循环应力-应变方程和应变-寿命方程中系数的拟合方法参考nCode理论手册，拟合数据见表1。表1中，*号的含义如下：1)当σb/E≤0.003时，φ=1；2)当0.003<σb/E<0.02时，φ=1.375-(125σb/E)；3)当σb/E≥0.02时，φ=0.1。

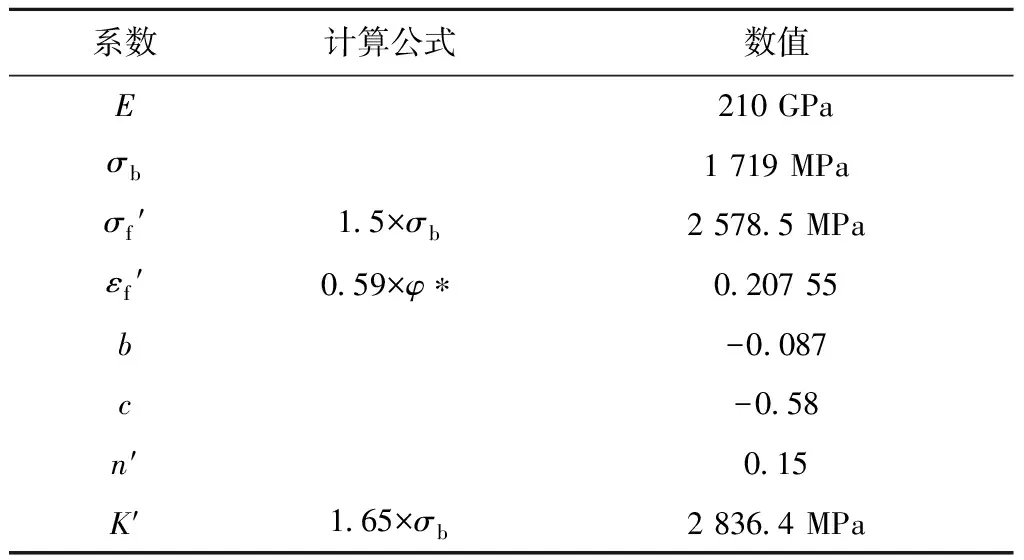
表1 疲劳寿命计算用拟合系数

在应力集中部位，应变-寿命方程预测的寿命通常比实际偏低，需要考虑基于应力梯度的应力修正，计算过程如下。

应力梯度示意图如图1所示。

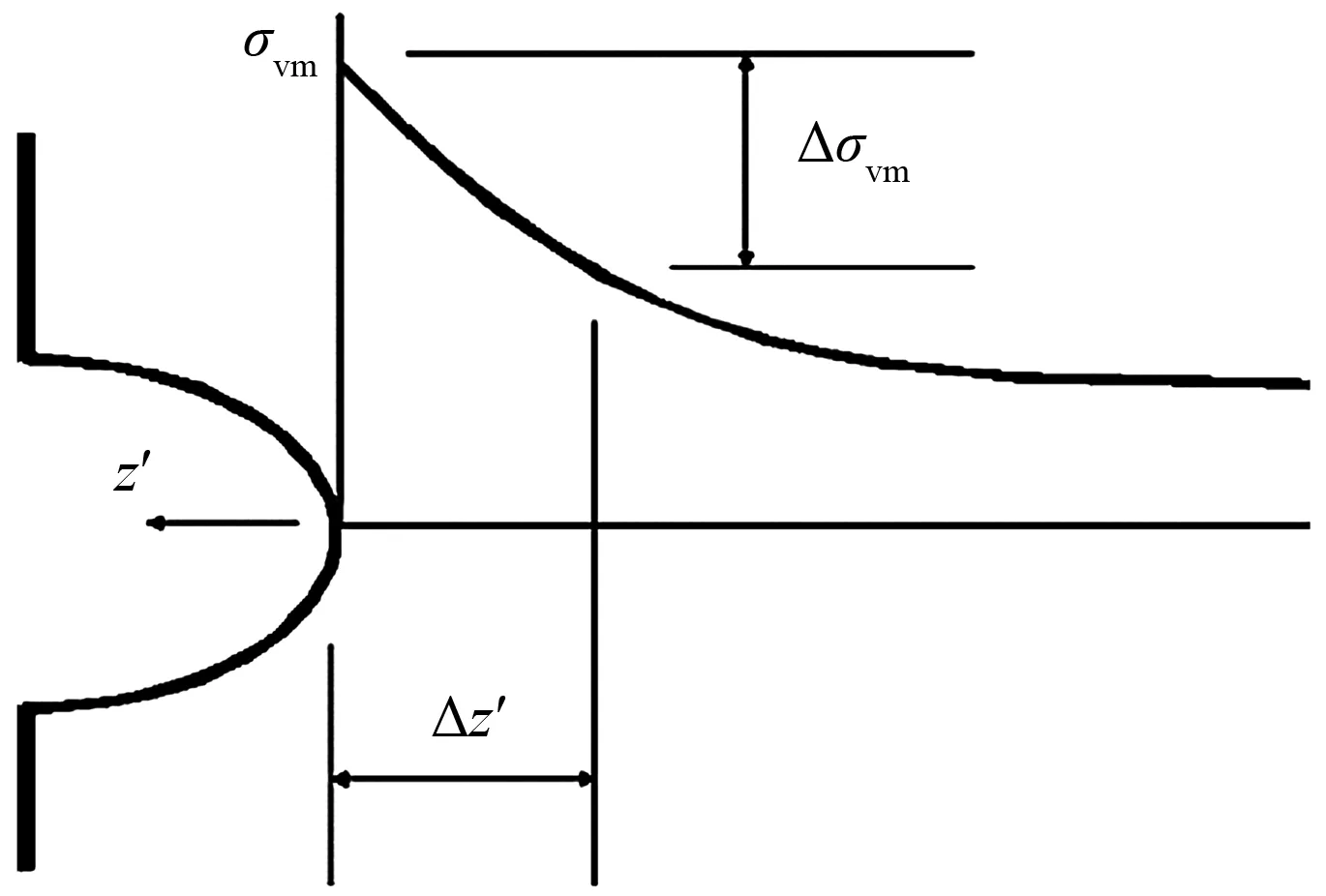
图1 应力梯度计算示意图

基于Mises应力梯度的计算公式如下：

基于应力梯度的应力修正系数nσ计算如下：

当Gσ≤0时，nσ=1

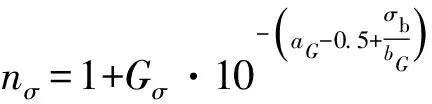
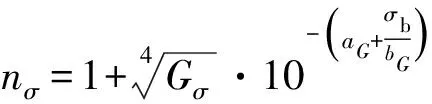
对于60Si2Mn材料，aG和bG分别取0.5和2 700。

2 计算模型和边界条件

2.1 计算模型

扭转弹簧三维装配模型如图2所示。为了简化分析，降低对计算机的性能需求，抓住问题的主要矛盾，取芯轴和扭转弹簧进行有限元仿真分析。扭转弹簧用六面体扫略网格划分，芯轴用四面体网格，网格划分结果如图3所示。扭转弹簧装配时，挡圈先预压39.7°锁住；工作时，压板继续施压，压板转动61°，扭转弹簧最终转动100.7°；然后压板回转，扭转弹簧回弹至挡圈，完成一个工作循环。

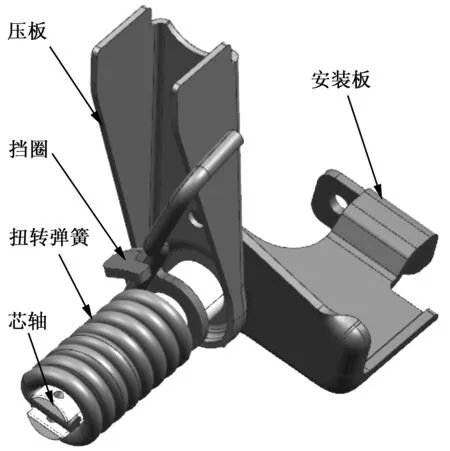
图2 扭转弹簧三维装配模型

图3 有限元网格模型

2.2 有限元分析设置

有限元分析设置如下。

1)扭转弹簧固定端和芯轴槽之间采用绑定约束，弹簧内外环表面与芯轴表面采用摩擦接触，摩擦因数取0.13。

2)压板加载端采用回转运动副简化，回转中心设在芯轴轴线上，约束关系示意图如图4所示。

图4 计算模型约束关系

3)有限元分析设置按实际工况进行，分2步进行加载。第1步：弹簧扭转39.7°；第2步：弹簧扭角61°，第2步结束时弹簧扭转总角度100.7°。

4)计算模型在芯轴与安装板装配位置固定。

5)有限元分析设置中打开大变形，考虑几何非线性效应(100.7°大变形)。

3 静强度计算分析

3.1 线弹性计算

第1步载荷施加弹簧扭转角为39.7°，计算得到的弹簧Mises应力云图如图5所示，最大应力为1 415 MPa，未达到材料的屈服极限，最大应力位于弹簧固定端转角内侧，且弹簧内表面应力明显高于外表面，符合弹簧受力一般规律。

图5 弹簧扭转39.7°时的Mises应力分布

第2步载荷施加弹簧扭转角为61°，此时弹簧总扭转角为100.7°，计算得到的弹簧Mises应力云图如图6所示，最大应力为3 691 MPa，最大应力位于弹簧固定端转角内侧，由于最大应力已经超过屈服强度，但大部分区域仍处于弹性状态，因此只有弹簧内环近表面区域进入屈服(见图7)。

图6 弹簧扭转100.7°时的Mises应力

图7 弹簧扭转100.7°时的屈服面

弹簧扭转39.7°静水应力分布云图如图8所示，弹簧扭转100.7°静水应力分布云图如图9所示。从图8和图9可见，最大应力点位置处静水应力均为负值，代表材料受到压缩，这对疲劳寿命是有益的。

图8 弹簧扭转39.7°时的静水应力

图9 弹簧扭转100.7°时的静水应力

根据反力计算结果，弹簧扭转39.7°时对应的扭矩为10.6 N·m；弹簧扭转100.7°时对应的扭矩为28.6 N·m。

在最大应力部位取计算截面，用于计算名义弯曲应力，计算截面如图10所示，计算得到名义弯曲应力为1 542 MPa(见图11)。

图10 计算截面示意图

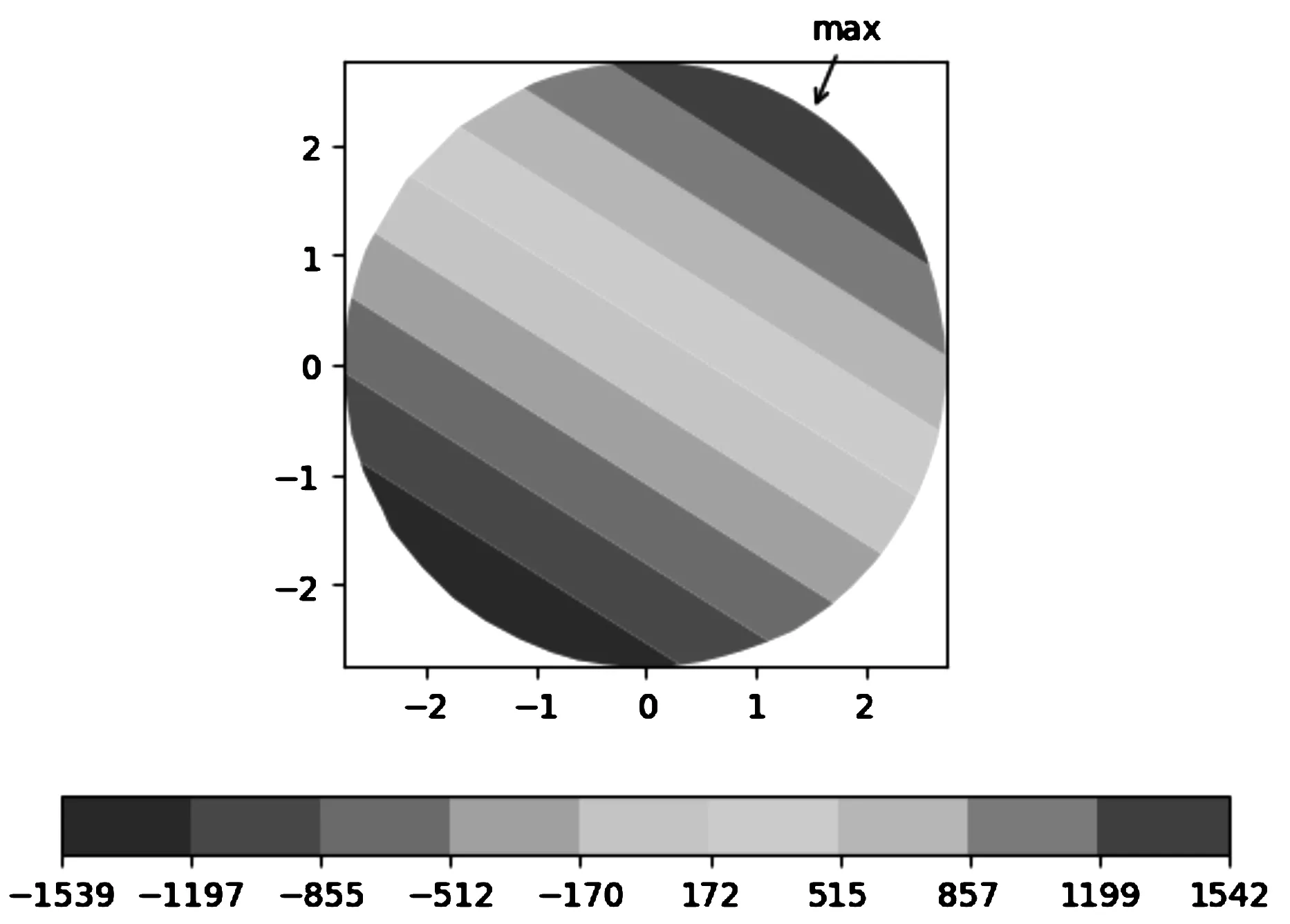
图11 名义弯曲应力

在远离应力集中部位取计算截面，用于计算名义弯曲应力，计算截面如图12所示，计算得到名义弯曲应力为1 443 MPa(见图13)。

图12 计算截面示意图

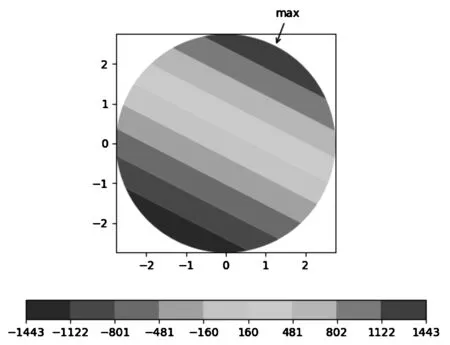
图13 名义弯曲应力

3.2 弹塑性计算

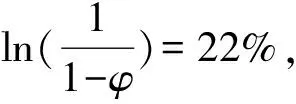
图14 弹簧扭转100.7°时的塑性应变

表2 理想弹塑性计算结果

用带切线模量硬化的弹塑性模型计算，弹簧扭转100.7°时，Mises应力如图15所示，最大应力为1 657 MPa，小于材料的强度极限(1 719 MPa)。

图15 弹簧扭转100.7°时的塑性应力

4 疲劳寿命计算分析

4.1 扭转弹簧疲劳寿命理论计算

沿着最大应力点所在面的法向往里建立路径，路径上应力如图16所示，计算得到最大应力点应力梯度Gσ=0.97 mm-1，应力修正系数nσ=1.072。

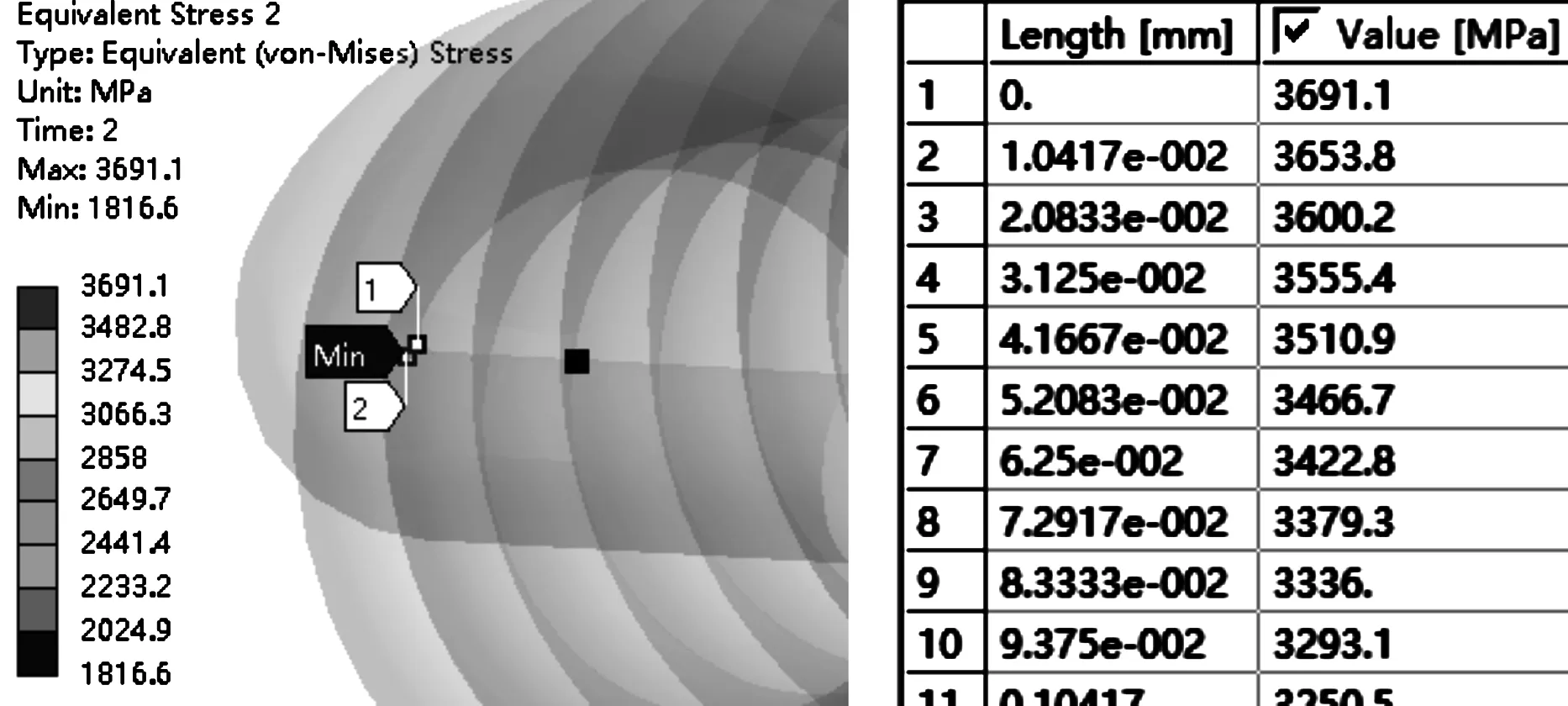
图16 路径应力分布

弹性应力循环范围为-1 415～-3 691 MPa。利用应力梯度修正系数修正应力，利用循环应力应变方程进行弹性应力修正，得到的应力应变迟滞回线如图17所示，最后利用Morrow方程计算得到弹簧的寿命循环数(见图18)，最小寿命循环数为1.06e5，位于弹簧固定端转角内侧。

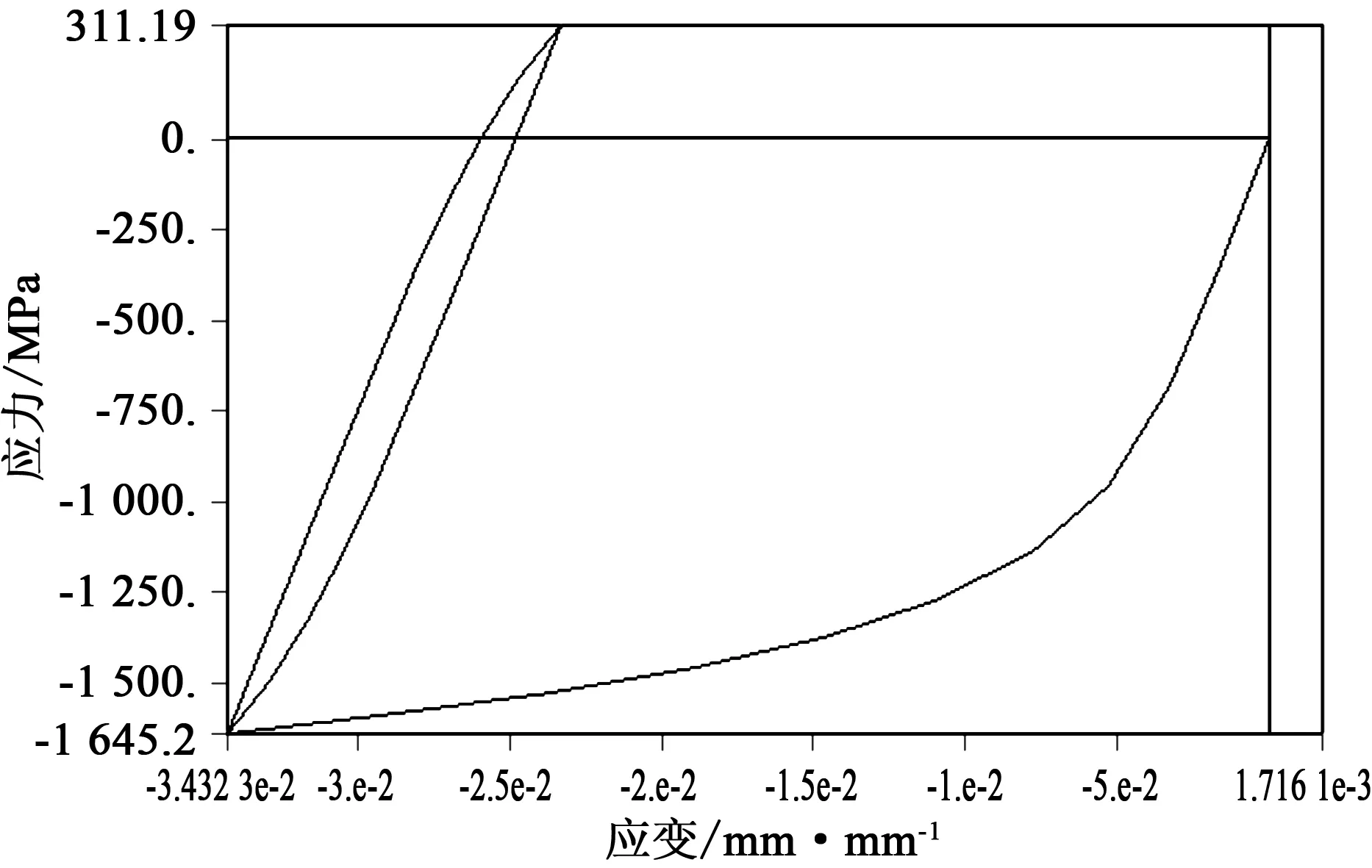
图17 循环应力应变迟滞回线

图18 寿命循环数云图

4.2 扭转弹簧实物循环疲劳试验

扭转弹簧疲劳试验台如图19所示。

图19 扭转弹簧疲劳循环试验台

疲劳试验断裂循环数统计结果见表3，断裂失效模式如图20所示。

表3 断裂循环数统计结果

图20 扭转弹簧断裂位置

4.3 试验结果分析

4.3.1 负载扭矩计算结果与试验结果对比分析

负载扭矩计算结果与试验结果对比分析见表4。从表4可知，材料模型采用线弹性模型和弹塑性模型，负载扭矩计算结果与试验结果均相差很小，弹塑性材料模型计算结果更精确。

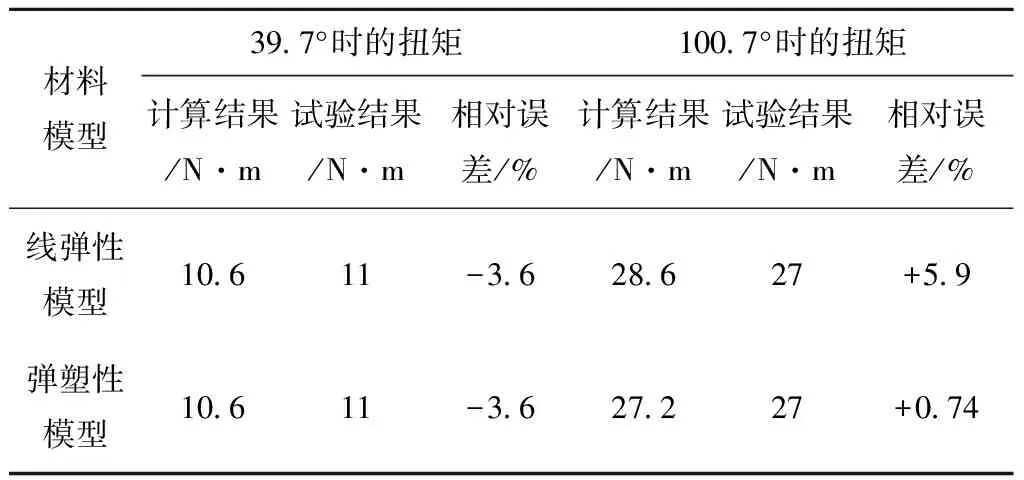
表4 负载扭矩计算结果与试验结果对比分析

从断裂失效模式(见图20)可见，断裂位置与仿真分析最大应力点位置相同，均在扭转弹簧折弯固定处。

4.3.2 断裂循环数计算结果与试验结果对比分析

将7组试验数据按照从小到大的顺序排列，计算均值、方差和标准差(见表5)[6-8]。

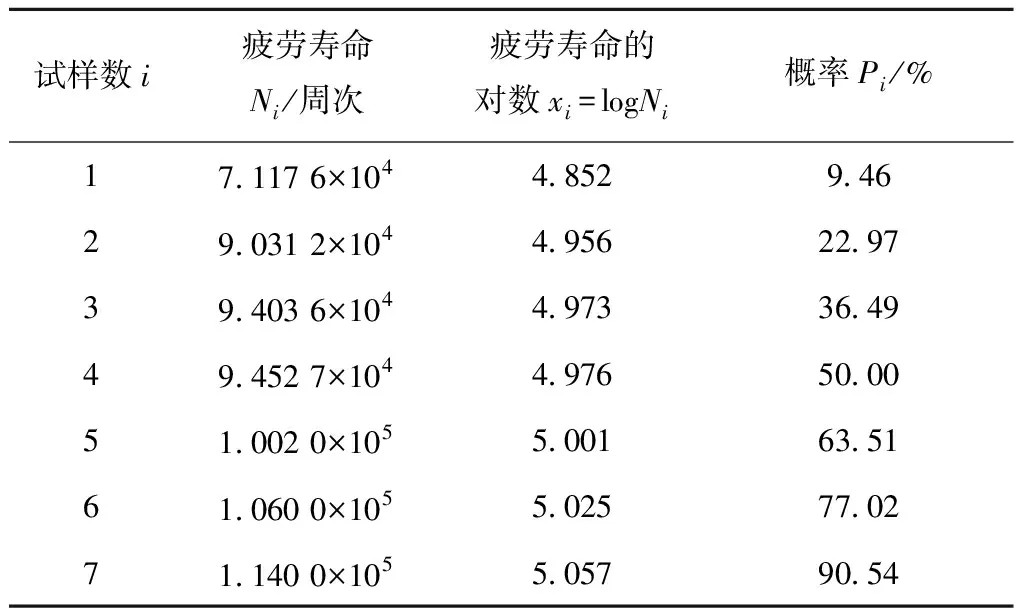
表5 试验数据统计分析

子样均值：

子样方差：

子样标准差：

95%置信度，10%失效概率下的疲劳寿命的下极限根据如下公式来估算：

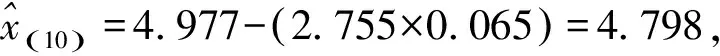
平均寿命：104.977=9.484 2×104cycles

扭转弹簧循环寿命仿真计算值1.06×105cycles，与试验平均寿命的比较如下：

绝对误差：

Δ=1.06×105-9.484 2×104=1.115 8×104

相对误差：

影响疲劳试验结果分散性的因素很多，主要有如下几个方面：1)试验设备的不精确性；2)试验材料的不均匀性，试件从原材料中不同的方位截取；3)试件尺寸和形状的不一致性；4)试件加工过程的不一致性；5)试件热处理过程的不一致性，如试件在热处理炉中所处的位置不同；6)试验环境的偶然变迁。

因此，名义上相同的一组试件的试验结果，总会存在一定的差异。仿真计算结果与试验结果相差11.76%，属于工程上可以接受的范围，计算方法有效。

5 结语

本文应用ANSYS Workbench软件对某扭转弹簧进行工作载荷下的疲劳寿命计算，结合产品实物疲劳试验进行对比分析，仿真计算结果与试验结果相差11.76%，属于工程上可以接受的范围，验证了疲劳寿命计算方法的有效性，为其他机械产品的疲劳寿命的确定提供了一套有效的计算方法。