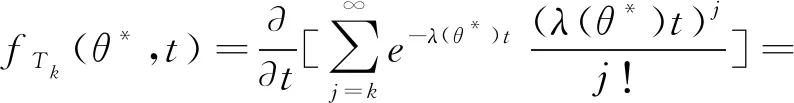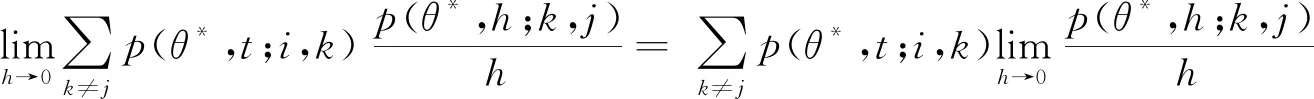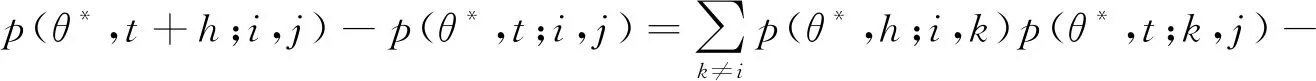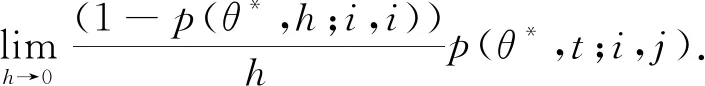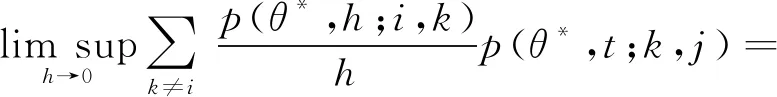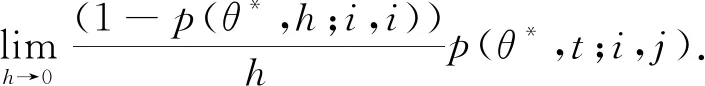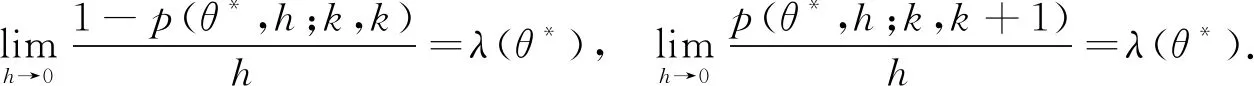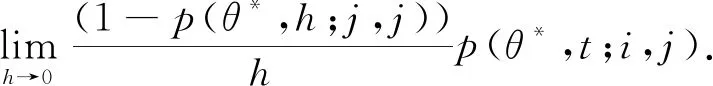随机环境中的泊松过程

单超超，吕 平

(杭州师范大学理学院，浙江 杭州 311121)

20世纪80年代初,Cogburn[1-2]首次将环境因素引入马氏链中,丰富并拓展了经典马氏链的理论体系.其后，得益于Hu[3-4]及其合作者们对随机环境中马尔可夫过程的推广和归纳整理，形成了一套完整的随机环境中马氏过程的理论体系，使得目前对随机环境中随机过程的研究有了较好的理论支撑和依据，其中不乏随机环境中马氏过程的分支.Palau等[5]研究了被布朗运动干扰的随机环境下连续状态分支过程，该过程以随机微分方程的唯一强解来构造，精确地给出其灭绝和爆炸概率，并给出了在非灭绝条件下的迁徙过程. Kuhlbusch[6]用鞅的方法来研究随机环境中的分支过程，推广了随机环境下一般分支过程和加权分支过程的早期研究结果.胡迪鹤[7]引进了随机转移矩阵、随机密度矩阵，进而引进了随机生灭q-矩阵及随机环境中的生灭过程概念，构造性地证明了随机环境中生灭过程的存在性.吕平等[8]引进了随机环境中一致马氏过程，给出随机环境中分枝q-过程存在性和唯一性的充分条件，证明了任意随机分枝转移密度矩阵都是零流入的.本文在前人工作基础上，引进随机环境中的泊松过程模型，推导出其转移概率，讨论了该过程与均匀分布和Γ分布之间的特殊关系，证明了当环境过程为坐标过程时随机环境中泊松过程是一类特殊的随机环境中马氏过程，最后给出该过程的随机Kolmogorov方程.这些对后续研究随机环境中的排队过程、生灭过程都有着重要意义.

1 符号及定义

令X是一个可数集，(Θ,B)是一个抽象的可测空间，R+=[0,∞),N={0,1,2,…},Θ表示环境，B是由Θ生成的σ代数.Θ*是从R+到Θ上的函数集，对每个θ*∈Θ*,s≥0,t>0,θ*[s,s+t)为θ*在[s,s+t)上的局限.

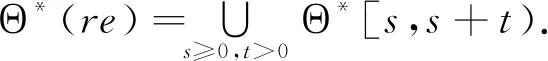
定义1令p(·;·,·)∶Θ*(re)×X ×X→[0,1]，如果

1)任意固定的s≥0,t>0和i,j∈X，p(θ*[s,s+t);i,j)作为θ*[s,s+t)的函数，关于(B[s,s+t))*可测；

3)满足随机Kolmogorov-Chapman方程：∀θ*∈Θ*,s≥0,t>0,u>0,i,j∈X有

则称p为Θ*上的随机转移函数.如果p(θ*[s,s+t);i,j)不依赖于s(对每个θ*∈Θ*,t>0,i,j∈X)，则称随机转移函数p是时齐的.

定义2设X=N，(Θ,B)是任一抽象可测空间，X*={Xt,t∈R+}，ξ*={ξt,t∈R+}是概率空间(Ω,F,P)上分别取值于X和Θ的两个随机过程，p为Θ*上时齐的随机转移函数.如果满足

1)X0=0;Xs≤Xs+t(∀s≥0,t>0);

2)对∀θ*,s≥0,t>0,i,j∈X，有

P(Xs+t-Xs=i,Xs-X0=j|ξ*[0,s+t)=θ*[0,s+t))=

P(Xs+t-Xs=i|θ*[s,s+t))P(Xs-X0=j|θ*[0,s))；

3)当t↓0时，对∀i有

则称X*是一个具有随机环境ξ*的泊松过程.

注1记号λ(θ*(0))首次出现在文[7]，因为随机转移函数关于时间t是时齐的，于是用0时刻的环境来描述，所以该记号在这里是合理的.

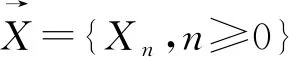
P(Xs+t=y|Xs=x,Xu,u∈[0,s))=p(θ;x,y)，

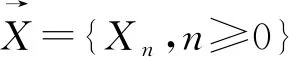
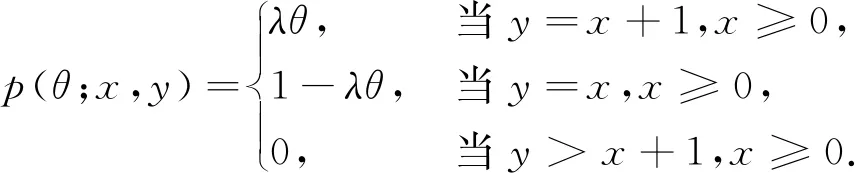
满足定义2的条件，因此现在该排队系统的到达过程为随机环境中的泊松过程.

下面着手推导随机环境中泊松过程的具体转移概率.注意到X0=0, 有

于是

P0(θ*,t+h)=P{Xt+h=0|θ*[0,t+h)}=P{Xt+h-X0|θ*[0,t+h)}=

P{Xt-X0=0,Xt+h-Xt=0|θ*[0,t+h)}=

P{Xt-X0=0|θ*[0,t)}P{Xt+h-Xt=0|θ*[t,t+h)}=

P0(θ*,t)[1-λ(θ*)h+o(h)],

因此

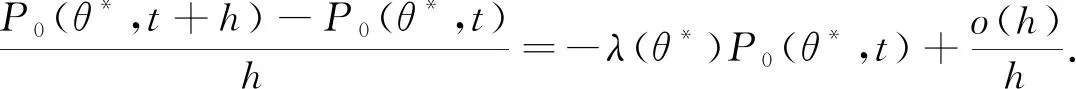
(1)

对式(1)两端取极限，令h→0，得

对t积分得到

P0(θ*,t)=k(θ*)e-λ(θ*)t.

(2)

因为P0(θ*,0)=1,代入式(2)得，对∀θ*∈Θ*有k(θ*)≡1，于是P0(θ*,t)=e-λ(θ*)t.

类似地，当n≥1时，

Pn(θ*,t+h)=P{Xt+h=n|θ*[0,t+h)}=P{Xt+h-X0=n|θ*[0,t+h)}=

P{Xt-X0=n,Xt+h-Xt=0|θ*[0,t+h)}+

P{Xt-X0=n-1,Xt+h-Xt=1|θ*[0,t+h)}+

Pn(θ*,t)P0(θ*,h)+Pn-1(θ*,t)P1(θ*,h)+o(h)=

(1-λ(θ*)h)Pn(θ*,t)+λ(θ*)hPn-1(θ*,t)+o(h),

于是

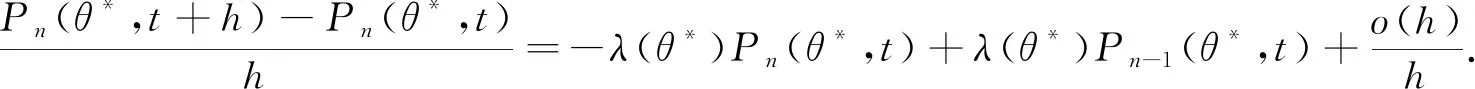
(3)

对式(3)两端取极限，令h→0，得

从而

因此

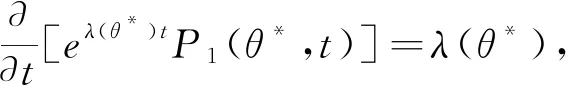
P1(θ*,t)=(λ(θ*)t+c(θ*))e-λ(θ*)t.

(4)

将P1(θ*,0)=0代入式(4)得，对∀θ*∈Θ*有c(θ*)≡0，因此

P1(θ*,t)=λ(θ*)te-λ(θ*)t.

对t积分得

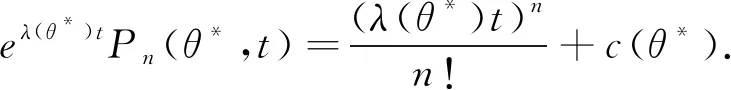
(5)

将Pn(θ*,0)=0代入式(5)得，对∀θ*∈Θ*有c(θ*)≡0，因此

成立，即随机环境中泊松过程的转移概率为

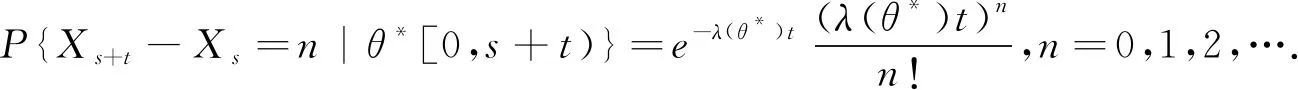
(6)

2 主要结果

本节将根据上文推导出的随机环境中泊松过程的转移概率，进一步讨论随机环境ξ*中的泊松过程X*具有的一些特殊性质.因为经典的泊松过程有平稳独立增量，事件在[0,t]的任何相同长度的子区间内发生的概率都是相等的.那么，在[0,t]内事件A只发生一次的前提下，A发生的时刻在[0,t]上是均匀分布的.由此，可推导出如下命题：

命题1(随机环境中泊松过程与均匀分布的关系) 设X*是一个具有随机环境ξ*的泊松过程，若在时间段[0,t]内只出现一个随机点，记T是其到达的时间，那么对∀ξ*,T～U[0,t].

证明因为[0,t]内只出现一个随机点，所以Xt=1.由式(6)知，对∀θ*∈Θ*，当s

由θ*的任意性知，T服从[0,t]上的均匀分布，对∀ξ*.

通过对泊松过程样本路径的研究，发现它是一条跳跃度为1的阶梯函数.又根据泊松过程的平稳独立增量性，可推导出事件发生的时间间隔服从参数为λ的指数分布.进一步，根据指数分布是特殊的Γ分布及Γ分布的可加性，易得第n次事件发生的时刻服从参数为n和λ的Γ分布.在随机环境下的泊松过程模型中，通过对达到时刻和时间间隔分布函数的研究，得到如下命题：

命题2(随机环境中泊松过程与Γ分布的关系) 设X*是一个具有随机环境ξ*的泊松过程，Tk表示第k个事件的到达时刻，Z1=T1，Zk=Tk-Tk-1(k=2,3,4,…)，则Tk～Γ(k,λ(θ*)),Zk～Γ(1,λ(θ*)),∀θ*∈Θ*.

证明注意到在随机环境θ*下，事件Tk≤t与事件Xt≥k是等价的.因此对∀θ*∈Θ*，t>0，有

由此得到

从而

于是

因此，对∀θ*∈Θ*，随机环境中泊松过程的第k个事件的到达时刻服从参数为k和λ(θ*)的Γ分布.

接着考察随机环境ξ*=θ*下Zk的概率分布.假定Tk-1时刻的观测值是sk-1，于是事件[Zk>t|ξ*=θ*]等价于事件[Tk>Tk-1+t|Tk-1=sk-1,ξ*=θ*]，也等价于事件[Xsk-1+t-Xsk-1=0|ξ*=θ*].因此

P(Zk>t|Tk-1=sk-1,ξ*=θ*)=P(Xsk-1+t-Xsk-1=0|ξ*=θ*)=e-λ(θ*)t,

于是可得随机环境ξ*=θ*下时间间隔Zk的分布函数

因此随机环境中泊松过程的时间间隔长度Zk在ξ*=θ*下服从参数为1和λ(θ*)的Γ分布.

从经典马氏过程的研究看出，如果有一个随机因素干扰原随机过程的转移概率，原过程未必还有经典的马尔可夫性.Hu在文[3]中首次引入随机转移函数p(·;·,·)以及随机环境中的马氏过程模型.将环境因素引入经典的泊松过程，并且假设接下来考虑环境过程为坐标过程，有如下定理：

定理1随机环境中泊松过程是依时的随机环境中的马尔可夫过程(MPTRE).

证明由定义2及MPTRE的定义知，只需证明∀s≥0,t>0,u>0,A∈A,B∈B,有

P(Xs+t∈A,θs+t∈B|Xu,u∈[0,s],θv,v∈(0,s+t))=

P(θ*[s,s+t);Xs,A)P(θs+t∈B|θv,v∈(0,s+t)),a.s..

(7)

设A={j},Xs=i(i≤j)，于是

P(Xs+t∈{j},θs+t∈B|Xu,u∈[0,s],θv,v∈(0,s+t))=

P(Xs+t-Xs=j-i,θs+t∈B|θv,v∈(0,s+t))=

P(Xs+t-Xs=j-i|θv,v∈(0,s+t))P(θs+t∈B|θv,v∈(0,s+t))=

P(θ*[s,s+t);Xs,{j})P(θs+t∈B|θv,v∈(0,s+t)),a.s..

因此，随机环境中的泊松过程是依时的随机环境中的马尔可夫过程.

如果将式(7)替换为

P(Xs+t∈A,θ*[s+t,∞)∈B[s+t,∞)|Xu,u∈[0,s],θv,v∈(0,s+t))=

P(θ*[s,s+t);Xs,A)P(θ*[s+t,∞)∈B[s+t,∞)|θv,v∈(0,s+t)),a.s.,

(8)

其中A∈A,B[s+t,∞)∈B*[s+t,∞),t>0,s,s+t∈[0,∞)，则称(X*,θ*)为依时的一致的随机环境中的马尔可夫过程(UMPTRE).同样的，若随机环境中的泊松过程满足式(8)，则称X*为依时的一致的随机环境ξ*中的泊松过程.

Hu在文[4]中给出了随机环境中马氏过程的Kolmogorov微分方程，随机环境中泊松过程作为一类特殊的随机环境中马氏过程，下文将讨论随机环境中泊松过程的Kolmogorov方程.

定理2(随机Kolmogorov方程) 设X*是一个具有随机环境ξ*的泊松过程，且对任意的θ*∈Θ*,λ(θ*)<∞，则对∀θ*∈Θ*,s≥0,t>0,i,j∈X有

1)随机Kolmogorov向后方程

证明1)根据定义1的3)有

变形得到

(1-p(θ*,h;i,i))p(θ*,t;i,j).

(9)

对式(9)两端取极限，令h→0，得

(10)

考虑到泊松过程状态是无限的，为此首先需要解决极限与求和运算顺序的交换问题.对固定的正整数M∈N，有

根据M的任意性有

又因为

同样地，根据M的任意性有

因此

于是可将式(10)变形得到

(11)

又根据定义2的3)，对∀k∈X有

(12)

代入式(11)有

因此，随机Kolmogorov向后方程得证.

2)类似地，根据定义1的3)有

变形可得

于是有

(13)

又根据假设，式(13)中极限与求和运算顺序可交换，因此式(13)可变为

(14)

最后利用式(12)的结果代入式(14)得到

因此，随机Kolmogorov向前方程得证.

注2因为随机转移函数关于时间t是时齐的，随机转移函数关于t的可导性无特殊要求.