纯粹的破损过程的群体平衡方程的对称及精确解

林府标，张千宏

(贵州财经大学数统学院，贵州 贵阳 550025)

0 引言

1872年奥地利物理学家Boltzmann提出的Boltzmann方程与1916年波兰统计物理学家 Smoluchowski提出的离散和连续型Smoluchowski方程,均是群体平衡方程的经典代表.群体平衡方程不但历史悠久而且应用广泛[1-7],如可用于探索大气物理学中的气溶胶聚并[6-7],研究血液中血小板聚集的动力学行为[3-4]等.实体工程科学应用领域最困难的问题不是如何依据实体粒子的动力学行为建立群体平衡方程模型,而是没有精确求解这些方程的理论和方法途径,故其研究方法大多采用数值实验技术和近似解析逼近方法[1-7].

本研究在前人工作[1-7]的基础上建立和分析不带消沉项仅具有纯粹的破损过程的积分-偏微分方程(群体平衡方程)模型.首先假设F(x,t)代表粒子的平均数量密度函数,t表示时间,x表示粒子的尺寸如体积或质量等.为了研究粒子在任意t时刻种群分布的状态,通常假设函数F(x,t)足够光滑,即关于变量x和t的任意阶偏导数都连续.粒子密度分布函数的一阶矩M1(t)定义为

(1)

(2)

连续累积质量分布函数f(x,t)随着粒子尺寸x的逐渐增大而严格递增,并且对尺寸足够大的粒子满足归一化性质f(∞,t)=1,而对尺寸为零的粒子满足零初始值f(0,t)=0.为了研究粒子密度分布规律F(x,t),从纯数学角度转化为考虑函数f(x,t),利用函数F(x,t)的假设条件和式(2)，函数F(x,t)可以写成

(3)

运用P(x|y)表示尺寸为x的粒子破损成尺寸为y的概率,此概率密度分布函数通常根据实验观察、实践经验或模拟粒子的破损过程而得到.假设P(x|y)与时间t相互独立,且粒子的破损概率分布函数满足正则性条件

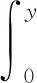
采用v(x,t)表示在t时刻粒子破损的平均数量,其最小值为2,如微生物种群细胞的分裂过程中v(x,t)=2.但因v(x,t)刻画的是粒子实体的平均值,实体工业领域使用时并非一定要为正整数.采用粒子的概率密度分布函数P(x|y)和破损的平均数量函数v(x,t)定义破损部分粒子的体积分数G(x|y)为

(4)

累积体积分布函数(4)满足性质G(0|y)=0,G(y|y)=1.

固体颗粒、种群粒子或微粒的破损或粉碎流程中,尺寸或质量小于等于x的粒子不可能通过破损而消失,但是它们可通过较大粒子的破损而不断形成.因此不含消沉项仅具有纯粹的破损过程的积分-偏微分方程(群体平衡方程)[3-4]可写成

(5)

假设破损频率函数b(x,t)、破损概率函数P(x|y)和粒子平均数量函数v(x,t)均与时间相互独立,破损频率函数b(x,t)关于粒子尺寸既满足齐次性又有幂率性.根据这些函数应该满足的条件和性质及实体工业领域的应用,考虑如下类型的函数：

(6)

其中k、n均为常数且k>0,n∈R.在约束条件(4)和(6)下,积分-偏微分方程(5)可简化成

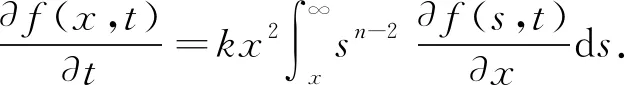
(7)

探究积分-偏微分方程(7)的对称及其精确解在实体工业的应用领域是有意义和重要参考价值的.经典的李群分析方法[8-11]虽然是计算、研究常微分方程和纯偏微分方程的对称及群不变解等的有效工具之一,但不能直接应用于积分-偏微分方程,如群体平衡方程(7).近年来，改进了的李群分析方法[12-13]已被用于群体平衡方程[14]、积分-偏微分方程、时滞微分方程和随机微分方程.采用这一方法探究积分-偏微分方程的对称、群不变解、约化积分-常微分方程及其精确解,最大障碍是写出决定方程和如何求解决定方程.因决定方程仍为积分-偏微分方程,其求解没有普适性的规律和方法可循,而是依赖于该方程本身固有的结构、特征及性质[12-16].

本文首先拟采用伸缩变换群分析方法[14]探寻积分-偏微分方程(7)所接受的伸缩变换群及对称.然后把积分-偏微分方程(7)转化为偏微分方程,利用经典李群分析方法研究此偏微分方程的对称,将偏微分方程所接受的对称结合积分-偏微分方程(7)所接受的伸缩变换群及对称得到积分-偏微分方程(7)所接受的对称、群不变解及约化的积分-常微分方程.采用观察试探函数法[14]发现约化的积分-常微分方程的精确解,最后获得积分-偏微分方程(7)的精确解及其种群粒子累积质量分布函数(3).

1 积分-偏微分方程(7)所接受的伸缩变换群

经典的伸缩变换群分析方法[9-10]常用于常微分方程和纯偏微分方程,目前用于积分-偏微分方程的文献资料极缺乏.困难是从常微分方程和纯偏微分方程到积分-偏微分方程不是类似顺推,因伸缩变换群会改变或者影响积分项的各种类型,故该方法对积分-偏微分方程是否有效,最关键因素之一就是积分项的类型.本文基于文献[14]的研究方法和理论，采用伸缩变换群分析方法探寻积分-偏微分方程(7)所接受的伸缩变换群及对称算子.假设积分-偏微分方程(7)所接受的单参数伸缩变换群为

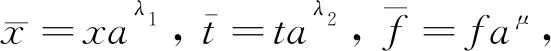
(8)

其中a为群参数,λ1、λ2、μ为任意常数.单参数伸缩变换群(8)对应的无穷小李对称算子为

(9)

(10)

通过计算化简整理得到

(11)

因此,积分-偏微分方程(7)和变换方程(11)给出了参数n、λi(i=1,2)所满足的群不变约束条件

λ2=-nλ1.

(12)

类似上述的推导方法和思路可证明平移变换群

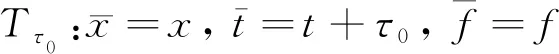
(13)

被积分-偏微分方程(7)所接受,其中τ0为群参数.将群不变约束条件(12)代入算子(9),依据参数λ1、μ的任意性和平移变换群(13)得到积分-偏微分方程(7)所接受的伸缩变换对称算子和平移算子分别为

(14)

2 积分-偏微分方程(7)所接受的李群

利用改进的李群分析方法[12-13]寻找积分-偏微分方程(7)所接受的李群,最主要的困难是求其决定方程的通解.一方面,积分-偏微分方程(7)的决定方程仍为积分-偏微分方程.其次,积分项固有的结构特征是下限为关于粒子尺寸x的变量.探寻其决定方程的通解没有成熟的相关理论方法、数学软件等可直接借鉴和参考.用此方法如何直接找到积分-偏微分方程(7)的对称值得探讨和摸索.

将积分-偏微分方程(7)转化为纯偏微分方程,然后采用经典的李群分析方法[8-11]对此方程进行研究.在积分-偏微分方程(7)两边同时除以x2,再关于粒子的尺寸变量x求导整理得到

L(f)=xfxt(x,t)-2ft(x,t)+kxn+1fx(x,t)=0.

(15)

由于方程(15)是二阶纯偏微分方程,故经典李群分析方法可直接应用.事实上,假设方程(15)所接受的无穷小李对称算子为

ξx=Dx(η)-fxDx(ξ)-ftDx(τ),

τt=Dt(η)-fxDt(ξ)-ftDt(τ),ηxt=Dt(ξx)-fxxDt(ξ)-fxtDt(τ),

其中Dx、Dt分别是关于x、t的全微分算子.通过计算得系数函数ξx、τt、ηxt的表达式分别为：

ξx=ηx+ηffx-fx(ξx+ξffx)-ft(τx+τffx),

τt=ηt+ηfft-fx(ξt+ξfft)-ft(τt+τfft),

ηxt=ηxt+ηxfft+(ηft+ηffft)fx+ηffxt-fxtξx-fx(ξxt+ξxfft)-

ft(τft+τffft)fx-ftτffxt-fxx(ξt+ξfft)-fxt(τt+τfft).

按照经典李群分析框架及算法[8-11],偏微分方程(15)的决定方程为

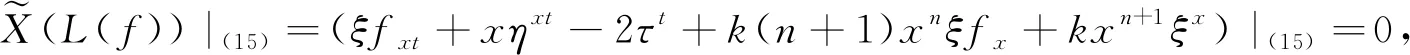
(16)

其中左下角标符号|(15)表示决定方程(16)对方程(15)的任一解均恒成立.利用方程(15)的变形表达式,即将fxt=2x-1ft-kxnfx及系数函数ξx、τt、ηxt分别代入决定方程(16)得到

ξ(2x-1ft-kxnfx)+x[ηxt+ηxfft+(ηft+ηffft)fx+(2x-1ft-kxnfx)(ηf-ξx)-

ft(τxt+τxfft)-fttτffx-ft(τft+τffft)fx-fxx(ξt+ξfft)+

(kxnfx-2x-1ft)(τt+τfft)]-2[ηt+ηfft-fx(ξt+ξfft)-ft(τt+τfft)]+

k(n+1)xnξfx+kxn+1[ηx+ηffx-fx(ξx+ξffx)-ft(τx+τffx)]=0.

(17)

ξft=0,ξff=0,τx=0,τf=0,ξt=0,ξf=0,ηff=0,

2(ξ-xξx)+x2ηxf=0,ηft+knxn-1ξ+kxnτt=0,xηxt-2ηt+kxn+1ηx=0.

由于ηff=0,所以函数η的表达式可写成η(x,t,f)=p(x,t)f+q(x,t),其中p(x,t)、q(x,t)为待决定的任意函数.将η(x,t,f)的表达式代入上面超决定方程,计算化简可得到pxt=0,τtt=0.故进一步可得决定方程(16)的通解为

τ=-c1nt+c2,ξ=c1x+c4x1-n,η=[(2x-n-knt)c4+c3]f+ζ(x,t),

其中ζ=ζ(x,t)为原方程(15)的任一解,ci(i=1,2,3,4)为任意常数.因此偏微分方程(15)的不变群的全体生成元构成一个无穷维李代数,它包含一个4维的子李代数L4=span{X1,X2,X3,X4},并有下列一组基：

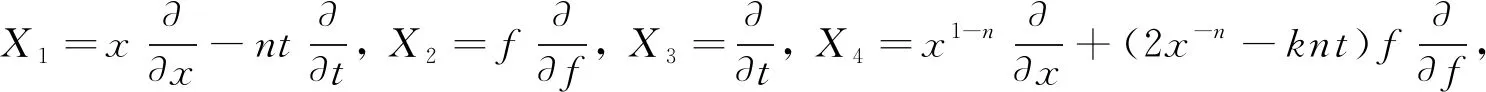
(18)

以及一个无穷维的子李代数L∞=span{Xζ},其无穷小李对称算子为

其中ζ=ζ(x,t)为原方程(15)的任一解.其无穷小李对称算子Xζ对应的李群为

其中b为群参数.采用类似伸缩变换群(8)被积分-偏微分方程(7)所接受的证明思路,将李群变换Tζ代入方程

F(x,t,f)+bF(x,t,ζ).

若n=0,利用算子(14)可知无穷小李对称算子X4=X1+2X2被积分-偏微分方程(7)接受.若n≠0,无穷小李对称算子X4对应的李群为

其中a为群参数.假设积分-偏微分方程(7)接受李群Ta,根据文献[12-13]的定义和算法,李群Ta应将积分-偏微分方程(10)的解变换成积分-偏微分方程(7)的解.但用类似(8)的证明方法,将李群Ta的变换关系式代入积分-偏微分方程(10),发现积分-偏微分方程(7)不接受李群Ta.因此获得定理1.

定理1偏微分方程(15)接受无穷小李对称算子(18)和Xζ,但积分-偏微分方程(7)未必接受全部的无穷小李对称算子(18)和Xζ.

定理2积分-偏微分方程(7)所接受的无穷小李对称算子构成一个3维的李代数L3=span{Y1,Y2,Y3},并有一组基Y1、Y2和Y3,见算子(14).

3 李代数L3的子李代数分类

研究积分-偏微分方程(7)的群不变解、约化积分-常微分方程及显式精确解,特别是探寻满足粒子实体意义的显式精确解,需要采用文[17]中算法构造李代数L3的换位子运算表、最优化子李代数分类系统,其中李代数L3的交换位子运算结果列于表1.

表1 李代数L3的交换位子运算表

采用表1获得相应的内自同构变换群分别为:

其中ai(i=1,2)分别为自同构群Ai(i=1,2)对应的群参数.因此对任意常数α李代数L3的一维、二维、三维最优化子李代数系统分别为：

span{Y2-Y3}, span{Y2+Y3}, span{Y1+αY2}, span{Y2}, span{Y3},

span{Y1+αY2,Y3}, span{Y1,Y2}, span{Y2,Y3}, span{Y1,Y2,Y3}.

4 积分-偏微分方程(7)的群不变解及精确解

运用李代数L3的一维最优化子李代数系统构造积分-偏微分方程(7)的群不变解、显式精确解和约化的积分-常微分方程.因积分-偏微分方程(7)中积分项的收敛性条件,导致一维子李代数系统span{Y2}和span{Y3}所对应的群不变解没有找到.对约化的积分-常微分方程利用观察试凑函数法[14]探寻其精确解,进而获得积分-偏微分方程(7)所对应的粒子的累积质量分布函数.

情形span{Y2∓Y3}算子Y2∓Y3对应的群不变量为J1=x,J2=exp(±t)f.因此可假设积分-偏微分方程(7)的群不变解的表达式为

f(x,t)=exp(∓t)φ(x),

其中函数φ(x)满足约化的积分-常微分方程

(19)

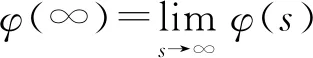
其中c为常数,函数φ(z)满足约化的积分-常微分方程

(20)

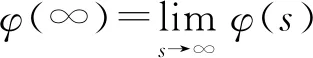
其中λ为积分常数.故利用平移变换群(13)的作用,得积分-偏微分方程(7)的显式精确解为

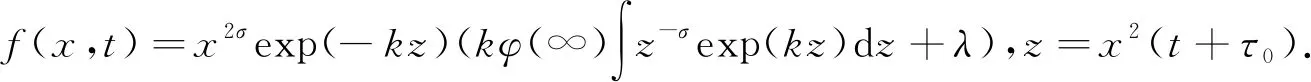
(21)

特别地当n=2时,对任意常数σ,函数φ(z)=zσexp(-kz)满足收敛性条件φ(∞)=0.因此,采用式(21)及粒子累积质量分布函数(2)的性质,得积分-偏微分方程(7)的精确解为

f(x,t)=x2σexp(-kx2(t+τ0))+1.

(22)

精确解(22)满足性质f(∞,t)=1.运用关系式(3)和(22)计算得到粒子的密度分布函数为

F(x,t)=2M1x2σ-2(σ-k(t+τ0)x2)exp(-kx2(t+τ0)).

(23)

精确解(23)满足动力学行为和性质F(x,t)→0,当t→∞或x→∞.这表明解(23)不但是渐进稳定的,而且对尺寸足够大的粒子其对应的种群密度分布函数必然趋于零.当σ=1时,精确解(23)对应的边界条件和柯西问题的初值条件分别为:

F(0,t)=2M1,F(∞,t)=0,F(x,0)=2M1(1-kτ0x2)exp(-kx2τ0).

当σ=1时,矩形区域[0,L]×[0,T]上种群密度分布函数(23)对应的边值条件和初值条件分别为:

F(0,t)=2M1,F(L,t)=2M1(1-k(t+τ0)L2)exp(-kL2(t+τ0)),

F(x,0)=2M1(1-kτ0x2)exp(-kx2τ0).

当σ≠1时,精确解(23)对应的边界条件和柯西问题的初值条件及闭矩形区域情形可类似讨论,为了行文简洁,略去.

选取参数σ=1,k=0.2,τ0=1,M1=0.1,粒子的累积质量分布函数(22)和对应的种群密度分布函数(23)在矩形区域[0,8]×[0,3]上的空间图像分别见图1(a)和(b).

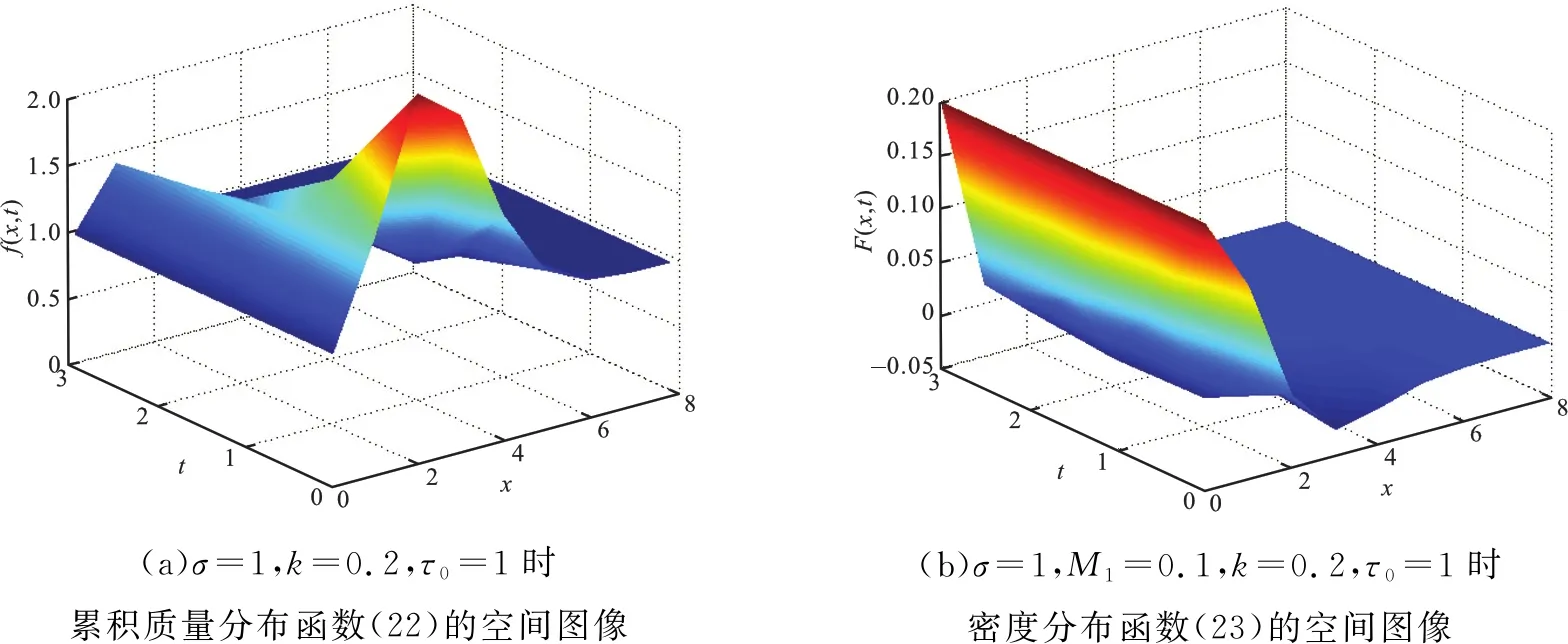
图1 当σ=1时粒子的累积质量和密度分布函数(22)、(23)的空间图像

类似地采用观察试探函数方法[14]探索积分-常微分方程(20),可获得其他类型的精确解,所得结果列于表2.相应的积分-偏微分方程(7)的精确解列于表3.利用方程(3)获得的对应的种群密度分布函数列于表4.

表2 约化积分-常微分方程(20)的显式精确解

表3 积分-偏微分方程(7)的显式精确解

表4 种群密度分布函数(3)的显式表达式

5 结论

经典李群分析方法[8-11]不能直接用于积分-偏微分方程(7).纯偏微分方程(15)所接受的无穷小李对称算子,积分-偏微分方程(7)未必都接受.本文采用经典李群分析方法[8-11]和伸缩变换群分析方法[14]找到了积分-偏微分方程(7)的对称、群不变解、精确解以及种群的密度分布函数.

如何直接利用改进了的李群分析方法[12-13]研究积分-偏微分方程(7)的对称,并构造新的精确求解方法探寻该方程满足实体模型更多的真实精确解,值得在今后的工作研究中探索和深思.