高速列车桥上等速交会时的车-桥耦合振动特性研究

王亚朋，蔺鹏臻，孙加林，李红梅

(1.兰州交通大学 土木工程学院，甘肃 兰州 730070；2.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081； 3.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心, 北京 100081)

两列列车高速交会时，车体表面产生的瞬态压力波将导致横向气动力，造成车体的剧烈晃动，对列车运行平稳性、安全性以及车体结构强度产生重要影响[1-2]。为保证列车的高平稳、高舒适及节约土地资源，高速列车线路大量采用以桥代路的方式。在桥上列车高速交会时，非定常侧向力会对列车稳定性产生重要影响，进而导致原有车辆-桥梁耦合系统动态平衡被打破，重新建立系统平衡状态[2-4]。对于列车交会横向气动效应等横向风荷载对车辆、桥梁系统的影响，国内外学者进行了大量研究，西岡隆等[5]、Diana等[6]、夏禾等[7]最先研究了横风对车-桥系统的影响。李永乐[8]、刘德军[9]、张楠等[10]考虑风、车、桥三者的相互作用，各自提出了风-车-桥系统空间耦合振动分析模型，并编制相应软件对横风下桥上行车问题进行研究。付连著等[11]、熊小慧等[12]、李人宪等[13]对不同线间距下高速列车交会时压力波特性进行了研究。赵晶等[14]对高速列车隧道内等速交会时气动力与速度的关系进行了研究。董亚男[15]对桥上列车交会时车体压力波进行了研究，结果显示桥梁结构会导致车体侧向力矩发生改变，因此桥上会车更加危险。

列车交会时由于车辆相对运动造成的非定常流动现象对列车运行安全性、舒适性产生重要影响，而高速列车交会时气动效应的准确模拟对于解决相关工程实际问题将起到至关重要的作用。本文针对适应更高速度发展的40 m简支梁桥，通过三维流体动力学计算方法准确求解，得出作用在列车上的空气压力波，并利用多体动力学理论建立了车-桥耦合分析模型，将空气动力学计算输出的力和力矩输入到车-桥系统耦合动力学模型中进行仿真分析[1]，建立了考虑列车交会气动效应的车-桥动力相互作用模型，研究桥上列车以更高速度交会时的车-桥耦合系统动力特性，以此提出高速动车组更高速度交会时的安全速度建议值，为进一步完善动车组超高速动态评估技术、大跨度桥梁结构动力设计等提供理论支撑。

1 考虑车辆交会的车-桥耦合动力相互作用分析模型

1.1 桥上列车交会系统模型

交会风-列车-桥梁系统是一个相互作用、相互影响的系统，两列列车相向行驶时，交会产生的气动效应对列车产生脉动响应，改变原有车辆运行状态，使其原有车-桥系统平衡重新构建[1]。基于多体系统动力学理论，车辆子系统与桥梁子系统通过轮轨关系耦合在一起，交会风压荷载作为车-桥系统的外荷载，施加到车-桥系统的车辆子系统运动方程的右端项中，从而建立考虑交会气动风压的车-桥耦合分析模型，如图1所示。

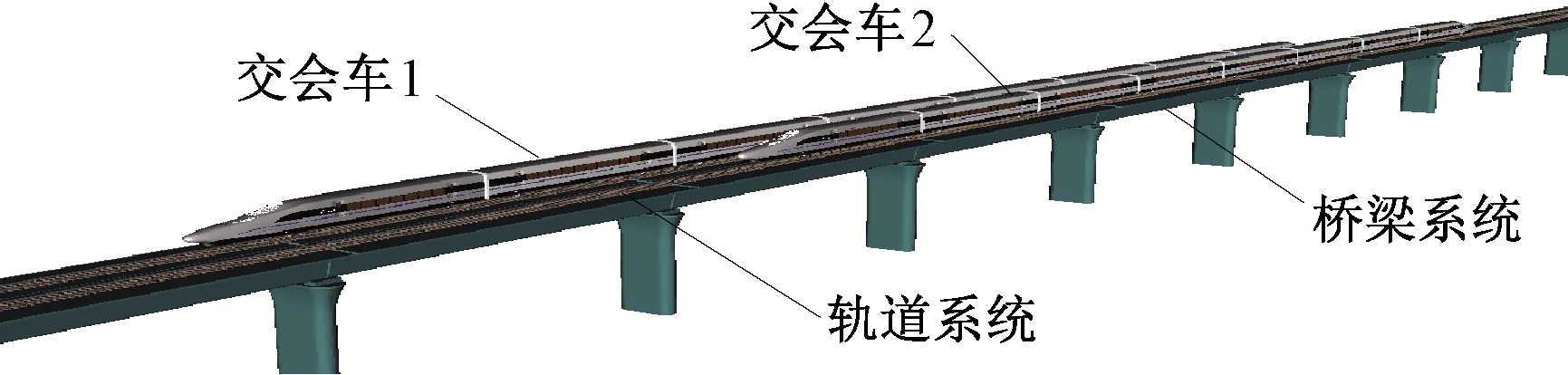
图1 考虑交会气动风压的车-桥耦合系统分析模型

1.2 车辆子系统模型

列车模型考虑轮对等各子部件的空间实际位置，每节车由15个刚体及一、二系悬挂系统组成，各刚体的自由度如表1所示。车辆子系统的运动方程可表示为

表1 车辆动力学模型各刚体自由度

(1)

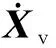
P=Fw+Pv

(2)

其中，Fw为车辆等速交会风压荷载列阵；Pv为轨道不平顺及桥梁各自由度振动状态函数。

1.3 桥梁子系统模型

在车-桥耦合分析模型中，一般认为桥上轨道板、底座板等与桥梁之间没有相互位移，并忽略橡胶垫及扣件变形，即桥梁变形与轨道变形一致[16]。因此，桥梁子系统采用有限元理论建立时，各节点运动方程可用模态表示为

(3)

2 列车交会空气压力波荷载分析

2.1 流场描述方程

两车交会时的车辆周围流场是可压缩、黏性、非稳态湍流流场[1,11]。对于可压缩黏性流体依然遵循物理学中的质量、动量、能量守恒定律，但该控制方程组在湍流状态下是非封闭的，因此对于列车交会这种复杂的流场流动湍流现象需引入湍流模型，因此总体控制微分方程[1]为

(4)

式中:ui(i=1,2,3)或uj(j=1,2,3)为列车周围流场速度；ρ为空气密度；xi(i=1,2,3)或xj(j=1,2,3)为坐标的三分量；p为压力；δij(i，j=1,2,3)为克罗内克符号；μ为空气动力黏度;cv为定容比热；E为总能量；T为热力学温度；τ为热传导系数；R为气体常数；μt为涡黏性系数；k为湍流动能；ε为湍流耗散率；Cu为湍流常数。

2.2 压力波数值模拟与结果验证

为了精确计算两车交会时周围空气流动的湍流现象，采用Fluent建立某高速动车组空气动力学模型，其中车内空气、车体结构均为弹性体，可考虑其变形，如图2所示。计算外域为长度2 453 m，宽200 m，高100 m的长方体。交会动车纵向车头相距1 053 m，线间距为5.0 m，距离计算区域后端500 m，动车组左右对称布置。计算区域采用分区对接网格技术，地面、列车均采用六面体结构化网格离散，各分区之间数据交换通过公共滑移界面进行，计算模型网格总数在1 000万以上。在列车运动方向上定义运动前侧为压力出口边界，后侧为进口边界，在流体与固体区域设置壁面边界，采用标准壁面函数模拟近壁面的流场流动，在列车与列车间、列车与计算区域间设定交互边界，不同区域数据通过交互面进行传递交换。采用Quick格式进行求解。

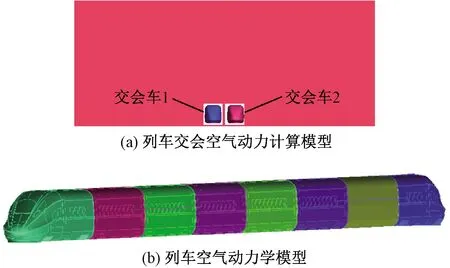
图2 动车组空气动力三维实体模型

为验证交会列车空气动力学模型的正确性，明线列车以速度400 km/h交会时相同测点风压试验与仿真的结果对比如表2、图3所示。由表2、图3可知该空气动力学模型计算结果与实测结果基本吻合，该计算模型结果可作为前述交会风压荷载计算。

表2 动车组明线交会仿真计算和实车试验结果比较(峰峰值)

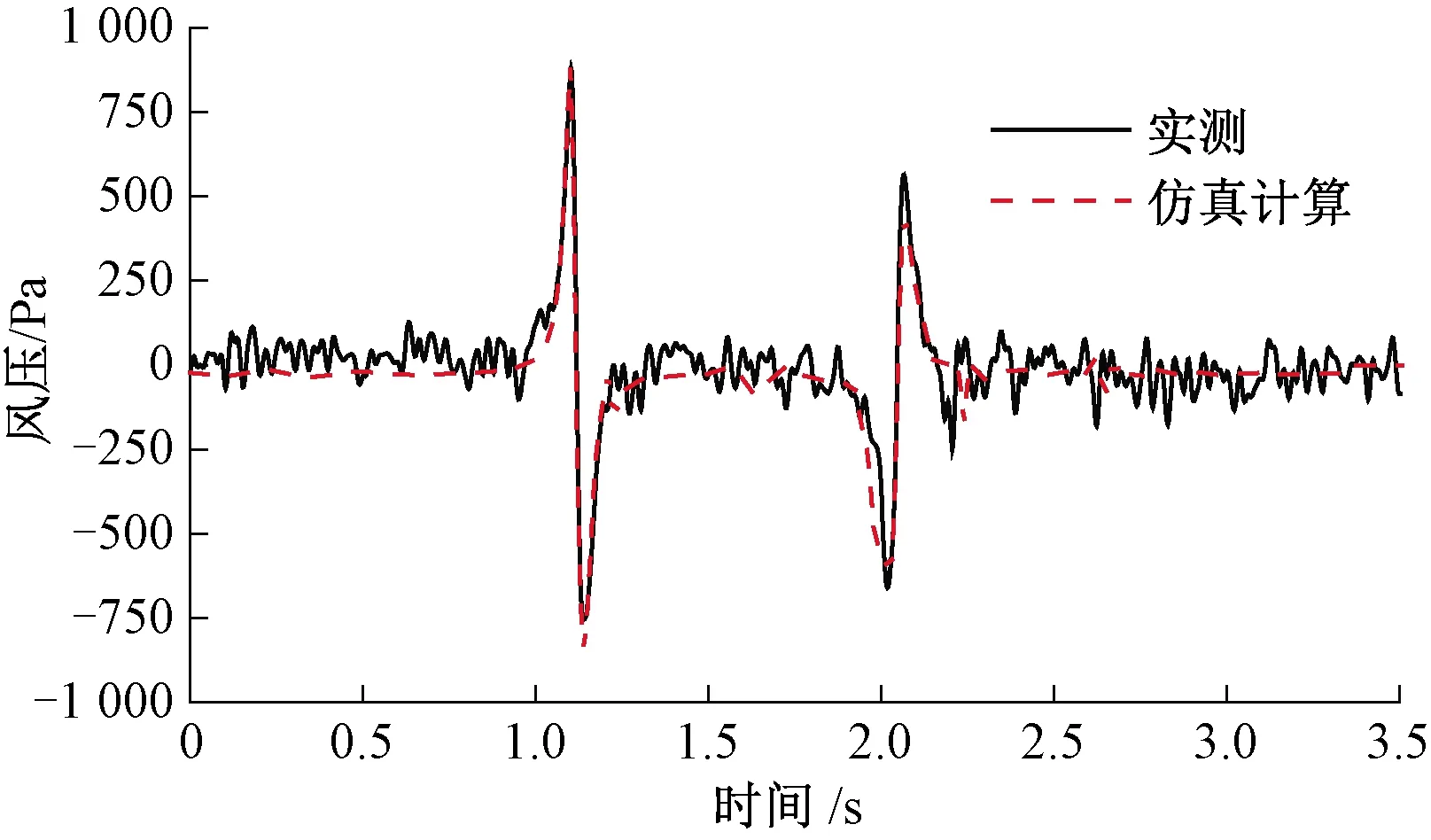
图3 明线交会时车身相同测点气压实测与仿真计算时程曲线

2.3 交会风压计算

车体运动可描述为六个方向的运动，故可将列车交会风压等效为车体质心点处力的时程曲线。因此参考文献[1]，将桥上列车以不同速度交会时产生的气动力以时程荷载形式施加到车辆子系统模型中，作用点位于车体质心处。本分析模型中将其等效为车体横向力、侧滚力矩和摇头力矩等，从而得到式(2)中Fw时程向量。按照上述方法，350 km/h交会时作用在头车上的风压等效荷载如图4所示。

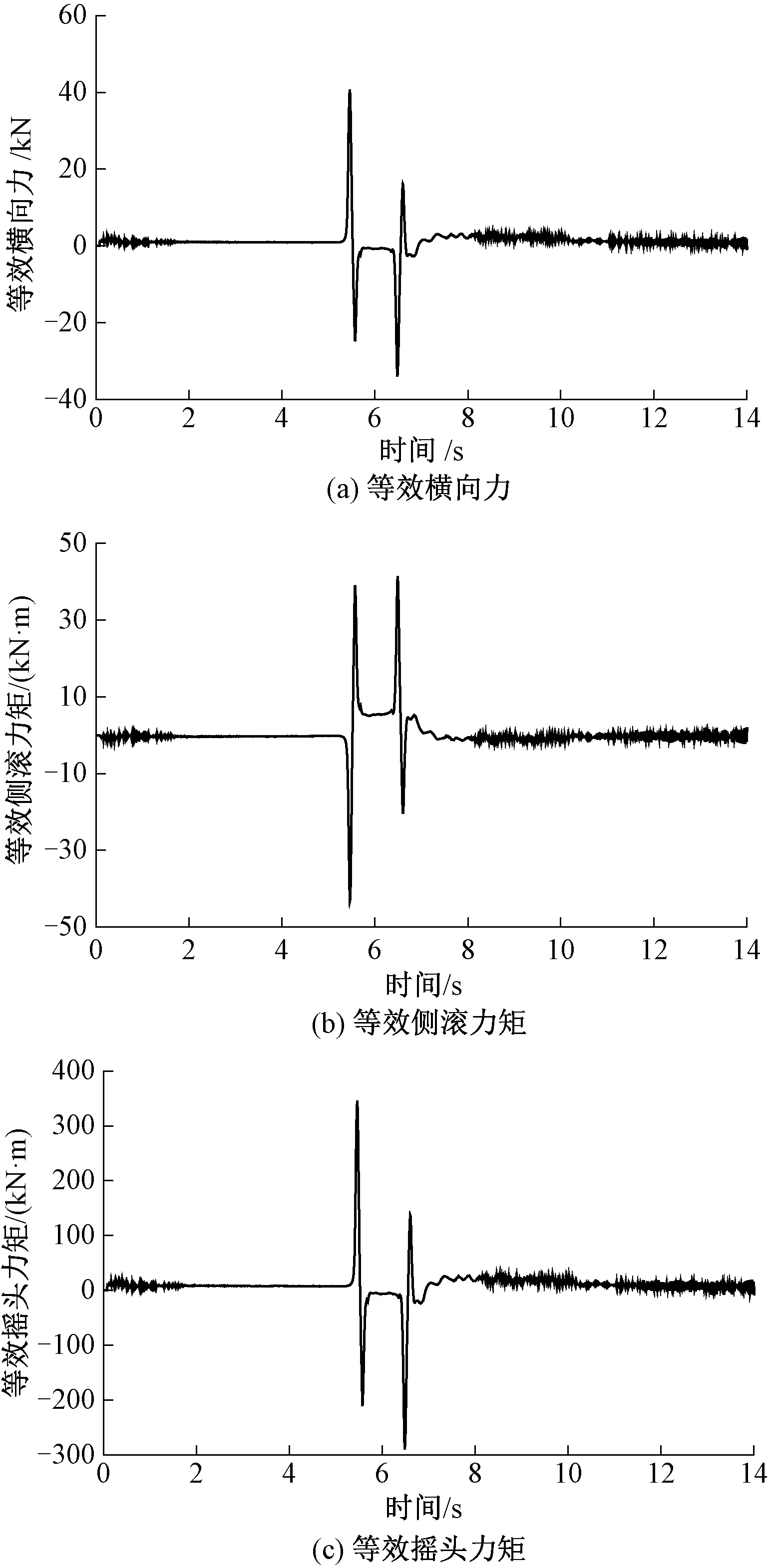
图4 头车等效风压时程曲线

3 桥上列车交会车-桥耦合振动分析

3.1 算例背景

以设计速度350 km/h的高速铁路40 m标准双线简支梁桥为例，分析该类型桥梁适应更高速度运行时双车桥上交会的动力特性。该桥桥面宽度1 260 cm，梁长4 060 cm，计算跨度3 930 cm，横向支座中心距为440 cm，梁高323.5 cm，截面如图5所示。

图5 箱梁1/2跨中-1/2支座截面 (单位:cm)

采用Ansys软件Solid185单元建立桥梁子系统三维实体模型，桥梁线路设备质量及附属设施等二期荷载采用Mass21质量单元模拟，二期荷载按照180 kN/m计算，边界条件按实际简支受力施工模型约束。采用UM软件建立空气动力计算同型号的8编组动车组车辆子系统模型，编组形式为拖+动+拖+动+动+拖+动+拖，车轮踏面为S1002 G型踏面，钢轨型面为中国60钢轨型面，名义滚动圆半径为920 mm，轮轨蠕滑力模型为多点非赫兹接触Kik-Piotrowski模型[17-18]。轨道激励选取中国高速铁路无砟轨道不平顺谱[19]，空间波长取1～30 m，高低、水平、方向、轨距不平顺时域样本曲线如图6所示。系统方程求解采用时间步内迭代法，每个时间步内通过子系统间的相互迭代，最终求得满足运动状态与作用力关系的解。

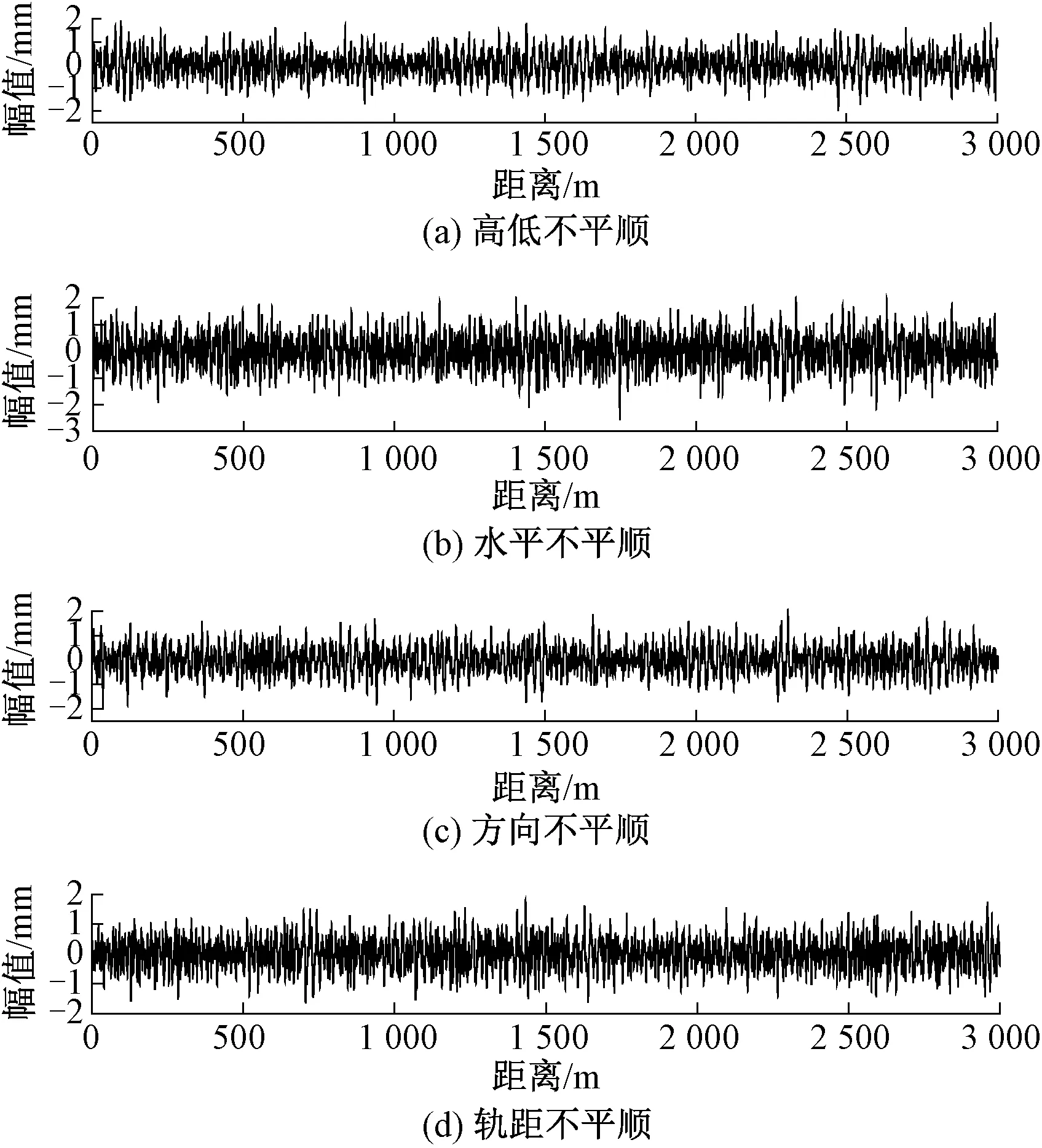
图6 轨道不平顺时域曲线

以速度350 km/h为基准，提高列车速度，对比分析交会车速的影响，各工况见表3。工况1和2对比风荷载对各指标的影响，工况2～5对比车速对各指标的影响。

表3 工况

3.2 列车安全性分析

图7为两列列车以不同工况交会时各安全性指标计算结果最大值对比。

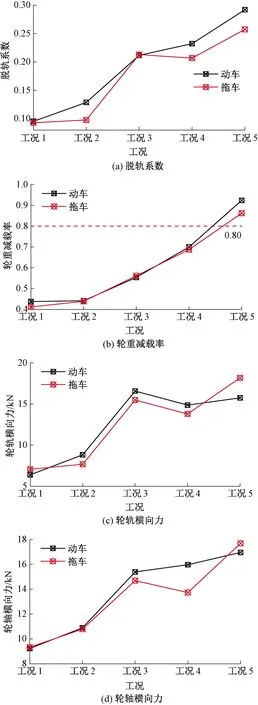
图7 不同工况交会时车辆安全性指标对比

对比分析工况1、2可知，桥上列车高速交会，不会对脱轨系数及轮重减载率产生较大影响，而对轮轨横向力及轮轴横向力影响较大。

对比分析工况2～5可知，列车各安全性指标随着交会车速的增大而逐渐增大，同时交会风压荷载对轮轨横向力及轮轴横向的影响较对脱轨系数及轮重减载率的影响更明显。

由图7(b)可知，在交会车速超过450 km/h后，轮重减载率将超过GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》[20]中0.8的限值要求，但轮重减载率主要是评定轮重因减载过大而引起脱轨的脱轨安全性指标，该指标受轨道几何不平顺状态的影响较大。因此，在现有高速列车及无砟轨道线路条件下，不宜进行450 km/h以上更高速度交会。

3.3 列车平稳性分析

图8为两列列车以不同工况交会时各平稳性指标的计算结果最大值对比。

图8 不同工况交会时车辆平稳性指标对比

对比分析工况1、2可知，桥上列车高速交会时，交会不会对车体竖向加速度、竖向Sperling产生明显影响，但会对车体横向加速度、横向Sperling及车体动态偏移产生较大影响，表明列车交会瞬间增大了车体横向振动加速度及车体横向偏移，同时降低了列车横向平稳性。

对比分析工况2～5可知，列车交会时车辆各平稳性指标随交会车速的增大而逐渐增大，且对拖车的影响较动车更加明显。因此，桥上列车高速交会时将会引发瞬间晃车，降低列车平稳性。

由图8(b)、图8(c)可知，交会车速超过350 km/h时，车体横向加速度将超过GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》[20]中动车组运行品质评定限值2.5 m/s2，交会车速超过450 km/h时车体横向Sperling指标将超过TB 10761—2013《高速铁路工程动态验收技术规范》[21]的限值3.0，因此两车交会时车速应控制在450 km/h以内较为舒适。

3.4 桥梁动位移分析

图9为两列列车以不同工况交会时桥梁不同测点位移计算结果最大值对比。

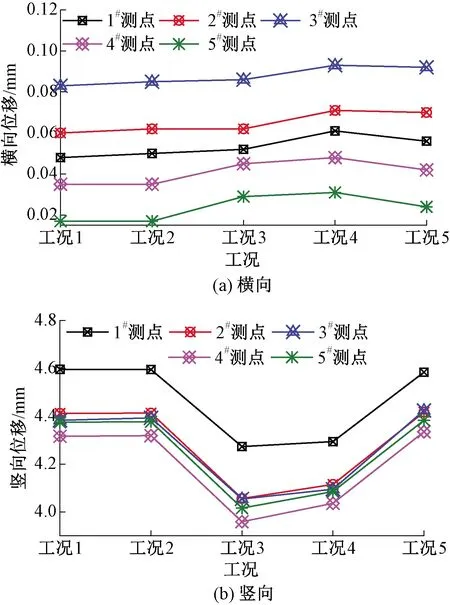
图9 不同工况桥梁跨中截面不同测点动位移对比

对比分析工况1、2可知，桥上列车高速交会时，交会风压对桥梁竖向位移基本没有影响，对横向顶板(1#～3#)位移有较小影响，而对底板(4#～5#)没有影响。

对比分析工况2～5可知，该跨度简支箱梁横向位移随着交会速度的增大呈先增大后减小的趋势，而竖向位移随着速度的增大呈现先减小后增大的趋势，该现象的出现是由作用到桥上的外荷载频率与分析模型的桥梁系统某些频率接近造成。

由图9可知，桥梁横向位移顶板普遍高于底板，且最大横向位移发生在顶板悬臂端处(3#测点)，桥梁竖向位移各测点基本一致，没有太明显的变化，最大竖向位移发生在顶板中心点处(1#测点)。

3.5 桥梁冲击系数分析

图10为两列列车车以不同工况交会时桥梁不同测点冲击系数。

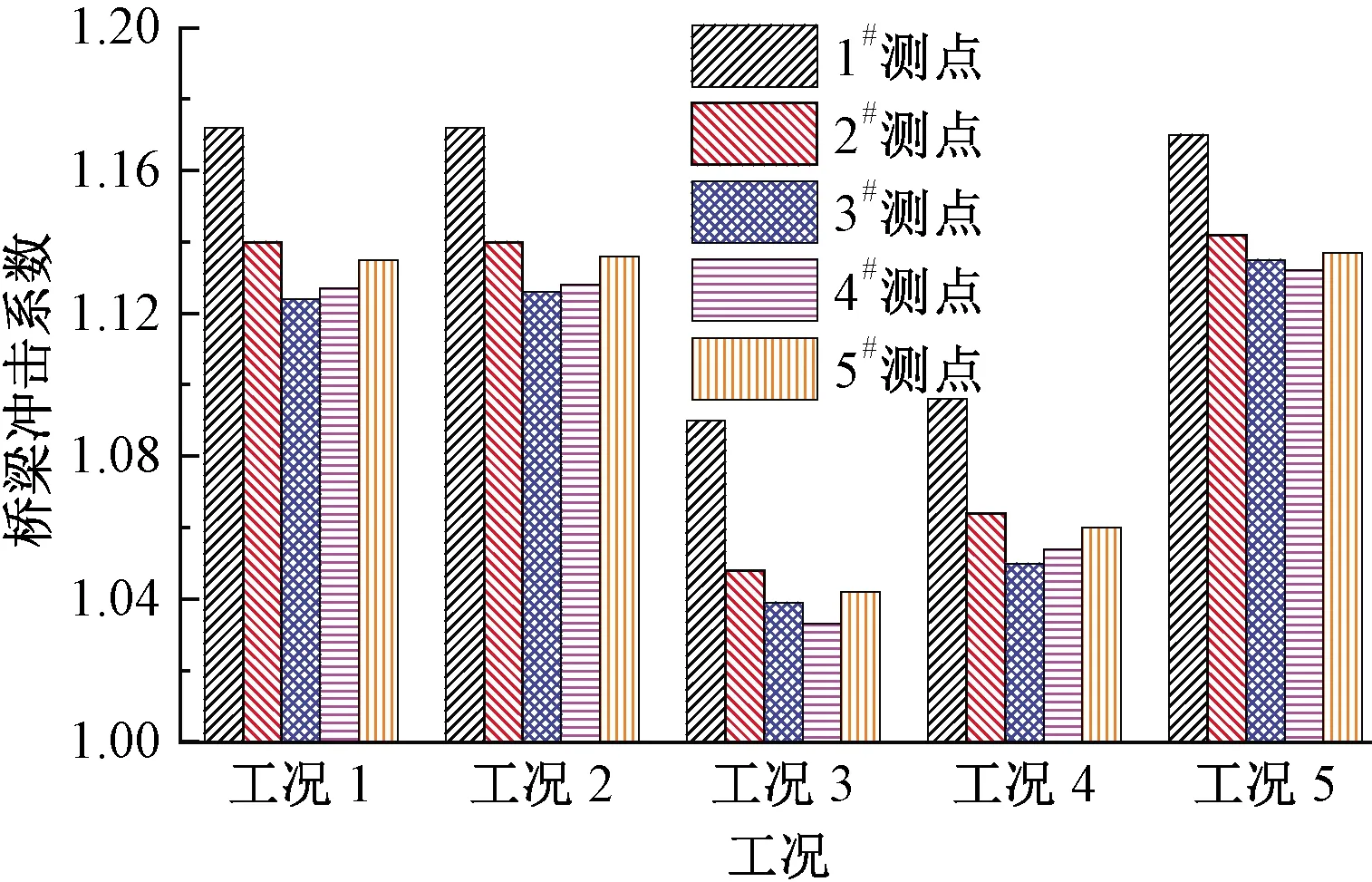
图10 不同工况交会时桥梁跨中冲击系数对比

对比分析工况1、2可知，桥上列车高速交会时，交会风压对桥梁冲击系数基本没有影响。

对比分析工况2～5可知，随着列车交会速度的增大，桥梁各测点的冲击系数会先减小后增大。对本算例40 m标准简支箱梁而言，列车以速度400 km/h交会时箱梁的冲击系数总体最小为1.03。

对本算例而言，箱梁顶板中心部位(1#测点)的冲击系数最大，为1.17，大于由TB 10621—2014《高速铁路设计规范》[22]计算的冲击系数1.06，顶板悬臂板端部(3#测点)的冲击系数最小，为1.13。因此由于箱梁存在空间结构效应，不同测量点的冲击系数不尽相同。

3.6 桥梁加速度分析

图11为两列列车以不同工况交会时桥梁不同测点加速度计算结果最大值对比，表4为桥面板不同测点在20 Hz强迫频率作用下竖向加速度最大值。

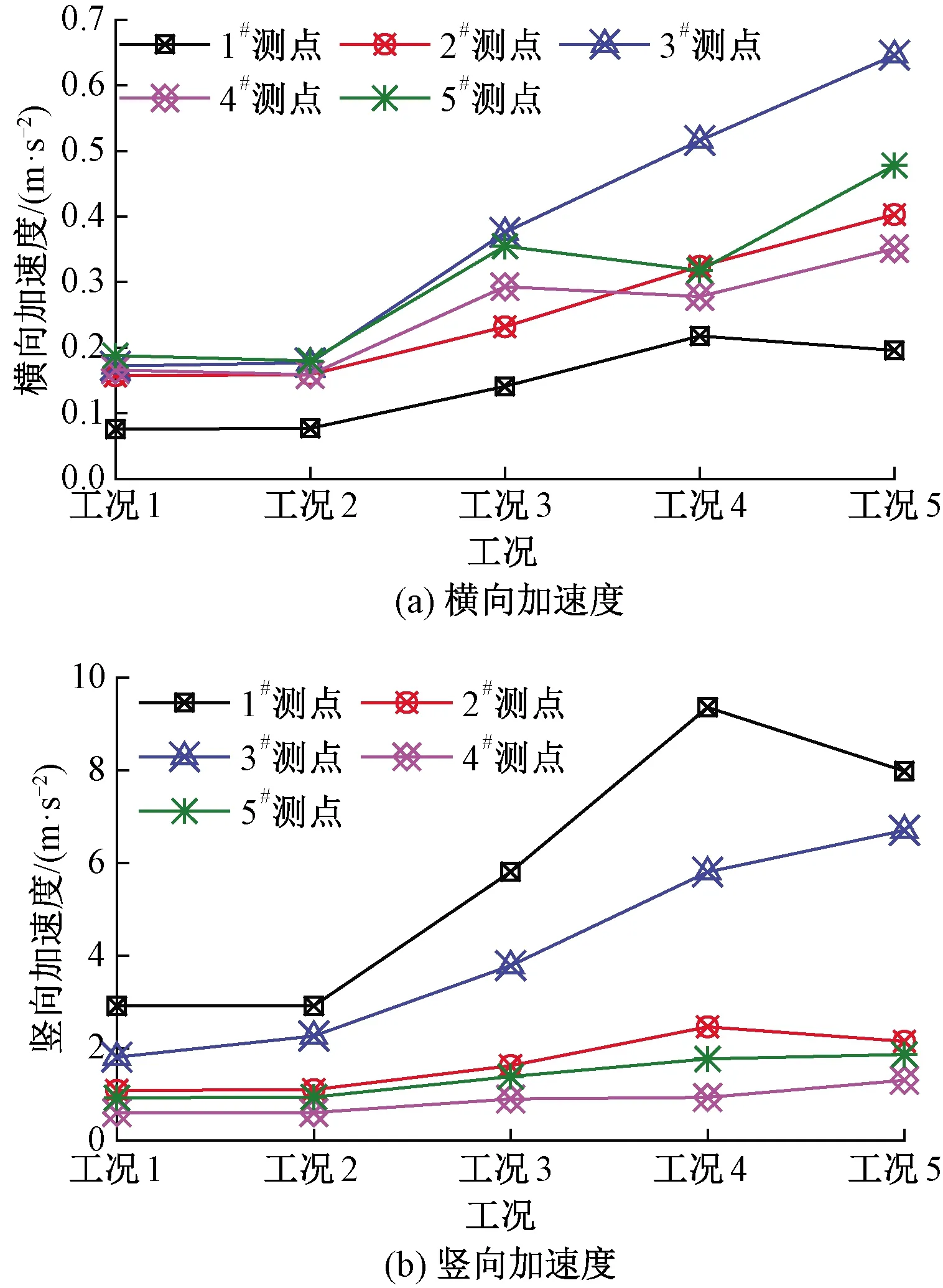
图11 不同速度等级交会时桥梁跨中截面加速度对比

对比分析工况1、2可知，桥上列车高速交会时，交会风压对桥梁横向加速度较竖向加速度影响更明显。

对比分析工况2～5可知，桥梁跨中加速度随着交会车速的增大呈现增大趋势，对竖向加速度而言，顶板中心点处(1#测点)和顶板悬臂端(3#测点)增大更明显。

由表4可知，桥面板各测点在20 Hz及以下强迫频率作用下竖向加速度最大为1.098 m/s2，小于TB 10621—2014《高速铁路设计规范》[22]规定的5.0 m/s2。

表4 桥面板不同测点20 Hz强迫频率作用下竖向加速度 m/s2

4 结论

(1)列车交会风压对列车轮重减载率、车体竖向加速度及竖向Sperling影响较小，而对脱轨系数、轮轨横向力、轮轴横向力、车体横向加速度、横向Sperling及动态偏移影响较大，随着交会车速的增大，车辆各指标呈现增大趋势。

(2)桥上列车交会时，由于交会风压会改变车辆作用频率，对桥梁的位移、冲击系数及加速度有一定影响。

(3)随着交会车速的增大，轮重减载率、车体横向加速度、横向Sperling等将超过现有规范限值。以车体横向加速度及横向Sperling为评判指标，两车交会车速应控制在450 km/h以下较为安全。考虑桥上列车高速交会后，桥梁冲击系数将总体大于现有规范取值，现有规范冲击系数取值方法将不适用。