基于PMFCC-DTW的轨道电路暂态故障诊断

杨 璟，王小敏，张文芳，郑启明，陈 磊

(1.西南交通大学 信息科学与技术学院，四川 成都 611756；2.英国伯明翰大学 伯明翰铁路研究与教育中心， 伯明翰 B15 2TT)

轨道电路是自动完成列车占用状态检查的铁路信号设备，其工作质量直接影响铁路运输的效率，也是列车安全运行的重要保障。轨道电路故障模式复杂，现场处理故障时间较长，严重影响铁路运输秩序，是铁路信号现场维护的难点。因此，探索各种智能诊断方法以缩短故障处理时间，提升轨道电路故障维护效率，正成为人们关注的热点。

目前，已有部分学者对ZPW-2000轨道电路故障智能诊断展开研究，如：基于神经网络算法[1-2]构造轨道电路相关变量与轨道电路相关故障的非线性映射关系，继而实现故障的识别分类；基于粗糙集和模糊认知图[3]对监测数据进行属性约简提取特征参数，构建分类器实现故障诊断；通过组合决策树[4]建立组合网络模型获取诊断规则，逐级压缩诊断范围最终完成多故障识别；利用相空间重构技术[5]对一维分路电流包络信号序列进行重构操作，提取补偿电容的故障特征，从而实现补偿电容故障的检测；基于集中监测系统获取的电压值或电流值[1，3-4]、机车或动检车采集的感应信号[2,5-9]，通过对稳态值进行分析处理，从而对轨道电路故障进行诊断。以上方法虽对故障机理明确或有较多历史故障信息的显性故障诊断精度较高，但在稳态条件下可能忽略正常与故障状态之间的暂歇性波动状态[10]，因其故障信息较少或无故障信息。然而如果只对正常和故障两种状态进行判别，很难满足铁路现场对轨道电路设备的诊断要求，因此对轨道电路暂态故障进行诊断尤为必要。

ZPW-2000轨道电路发生故障，其实质是轨道电路参数的突变，从而引发轨道信号幅值由暂态过渡到稳态[11]。若能基于集中监测系统对采集的轨道电路电压信号进行暂态分析，探究其暂态特性与轨道电路故障的关系，实现故障地面实时检测，则可提高诊断的便利性和时效性。

本文首先通过实地测试模拟故障获取数据，并对轨道电路故障时电压暂态波形进行分析，组合利用梅尔频率谱系数和动态时间规整算法建立轨道电路诊断模型；然后通过该模型利用主成分分析约简特征属性，再融入Fisher准则和K-means聚类选择合适故障模板，最终得到的模板具有清晰明显的特点。测试结果表明，基于集中监测系统与模型的使用，能够对轨道电路设备的多状态进行有效识别，提高诊断效率，为轨道电路的状态监测提供合理补充。

1 ZPW-2000轨道电路故障类别

1.1 ZPW-2000轨道电路组成

ZPW-2000轨道电路由轨面、发送端和接收端组成，其中发送端包括发送器、传输电缆和防雷单元，接收端包括接收器、衰耗器、传输电缆和防雷单元。发送端至接收端轨面等间距分布着补偿电容，相邻轨道电路区间由调谐区实现电气隔离。ZPW-2000轨道电路结构示意见图1。

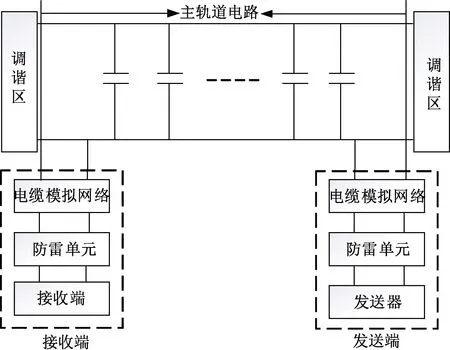
图1 ZPW-2000轨道电路结构示意

在集中监测系统中，反映轨道电路性能状态的主要指标是电压，因此本文采用轨道电路电压数据进行故障诊断，以轨道电路的多故障系统作为研究对象。轨入电压在一段时间内的电压状态曲线见图2，其按照时间的先后顺序可以分成三部分：正常、波动、正常。对于ZPW-2000轨道电路，在不同时间、地点、环境下其电压曲线波动情况会略有不同，但是总体上还是一致的。

图2 轨入电压曲线

1.2 故障类型

为了验证轨道电路暂态理论的合理性，通过分析故障产生的原因[12-13]，查阅现场实际案例的相关资料，并结合现场工作人员的历史经验，在西南交通大学轨道电路试验基地进行了常见故障的测试。故障采集系统包括硬件和软件两部分。硬件部分进行通信、自动切换测试点和采集模拟量等；软件部分进行发送指令、数据采集和存储等。测试的核心板卡选用NI-USB 6251，采样频率可达10 MHz，单点定位输出时序差分数据。针对不同故障的暂态过程进行数据采集，输出的数据具有噪声较小、精确度高等特点。使用LabVIEW中的DAQmx控件做上位机，图形化编写简单。测试系统结构见图3。图3中，主机确认采集点后，由DAQmx控件把采集命令传给采集卡，通过采集卡与室内设备通信，切换单元控件自动选择采集点，并通过采集卡将采集的数据传入计算机中存储。轨道电路故障模式见表1。

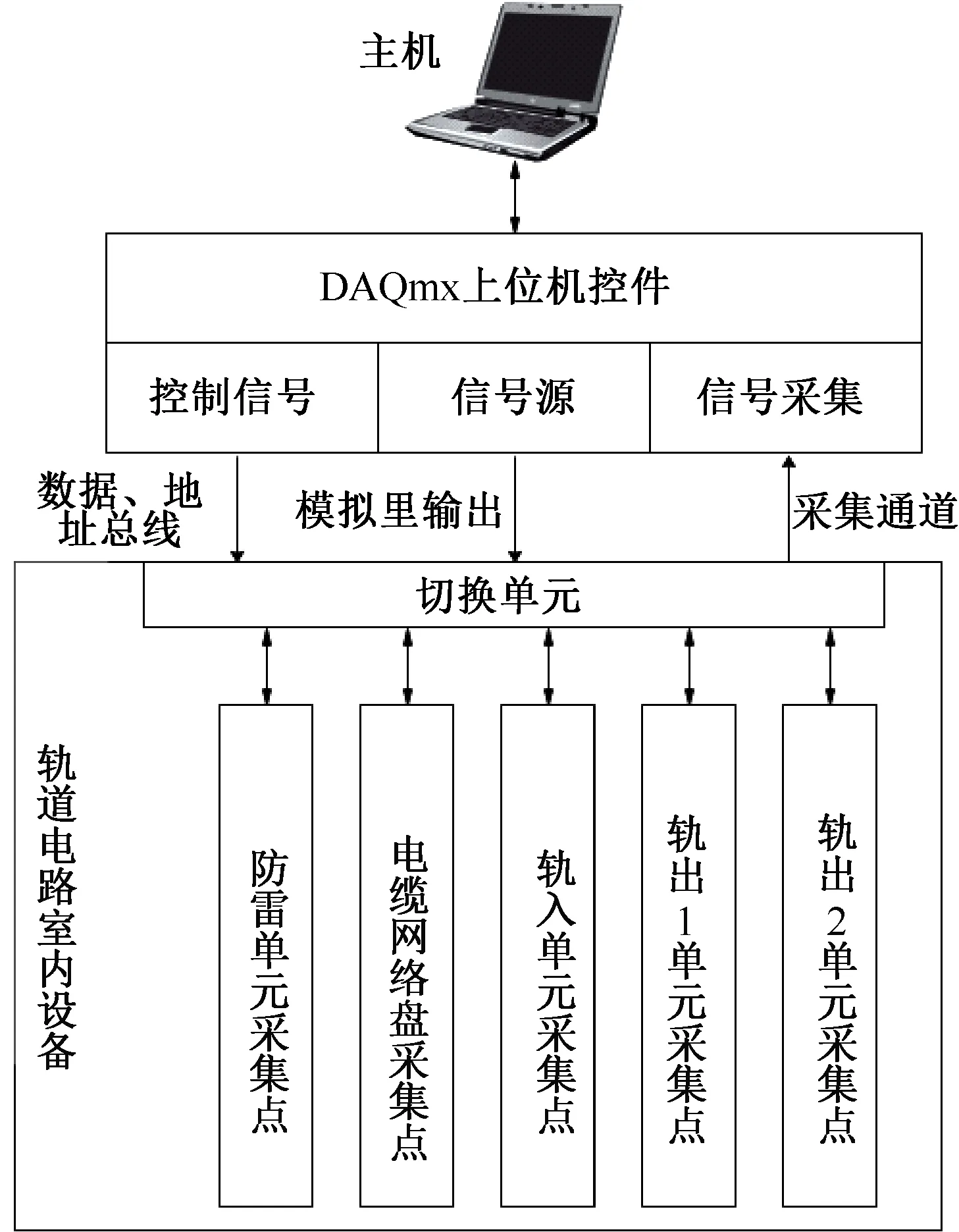
图3 测试系统结构

表1 轨道电路故障模式

对表1中8种故障类型每种随机各选一组提取包络，见图4。由图4可以看出,F1～F8故障的表现形式差异较为明显：F1为发送端故障，轨入电压短暂趋于0；F2为防雷单元故障，设备短时间内电压波动幅度较大；F3为电缆网络模拟故障，设备短时间内电压波动趋于0；F4为空心线圈断线故障，轨出1电压瞬间幅度降低；F5为调谐单元短路故障，轨出2电压瞬间波动幅度较大；F6为主轨故障，轨出2电压短时间波动幅度较大；F7为小轨故障，轨出1电压短时间波动幅度较大；F8为单个补偿电容断线故障，主轨电压瞬间降低。

图4 F1～F8的故障信号包络

图4展示了故障的发生会导致电压值的瞬间波动，工作状态发生跳变，可以较为直观地反映故障信息。但是，实际列车运行条件下设备会受到多方面影响，如天气、人为等因素，使故障波形不能直观精准反映故障位置，难以及时为维修人员提供有效的指导。因此，本文对ZPW-2000轨道电路的多种故障模式进行智能识别，组合使用PMFCC-DTW算法建立轨道电路诊断模型。

2 诊断模型基本原理

2.1 梅尔频率谱系数

梅尔频率倒谱(Mel-Frequency Cepstrum Coefficient, MFCC)在语音处理中表示一个语音的短时功率谱，由对数功率谱在频率的一个非线性梅尔刻度上进行线性余弦转换所得[14]。梅尔频率倒谱fmel与频率f的关系为

(1)

轨道电路在复杂的工况下，暂态故障通常是潜在的故障或早期的微弱故障，具有故障特征不明显、易被噪声影响的特点，使故障难以被发现。MFCC是按临界带宽由密到疏形成一组带通滤波器，对样本信号进行滤波，可以有效抑制非本频带的高频噪声成分。并且通过大量试验发现，当轨道电路发生故障时，不同状态下同一频带的信号频率基本一致，使用MFCC提取得到的不同状态下的特征各不相同，因此可以将MFCC用于轨道电路的故障诊断中。具体诊断过程如下：

Step1滤波输出为

H(z)=1-αz-1

(2)

Step2输出对数能量为

(3)

1≤m≤M

Step3提取梅尔系数为

(4)

式中：n为梅尔系数的数量；Ci(n)为第i帧的第n个MFCC系数；s(m)为对数能量模块的输出；M为Mel滤波器的个数。

由上述过程，依次获取8种故障的总采样点数，分别计算出每帧MFCC参数Sm和差分系数特征集Cn，约简后得到特征矩阵Mmel为

Mmel=|SmCn|

(5)

通过MFCC提取的特征能够精准地捕捉信号变化，但是信号特征维度较高，不利于可视化分析，更会导致诊断时间增长。因此，本文利用主成分分析(Principal Component Analysis，PCA)，对高维数据进行压缩，把可能具有相关性的高维变量合成线性无关的低维变量，新的低维变量集会尽可能保留原始信号的特征。组合MFCC和PCA，寻找和保留最有效、最重要的信号特征，从而降低计算复杂度、减少数据存储量，并且提高信号识别的效率。

2.2 动态时间规整

在模式匹配中，通常选用动态时间规整(Dynamic time warping，DTW)求解衡量不同信号间似然度的测度函数，也可以不要求每条故障数据长度严格对齐，允许在时间轴上的拉伸或压缩[15]。本文通过计算模板库和测试集中对应帧之间的失真距离，得出帧匹配距离矩阵，编制DTW表格。表格中的格点是对应的交汇点，按照距离最短原则搜索格点，反复递推得到组最优解，并将累积距离最小的归为此类故障。

将实测数据分为测试故障和故障模板，分别为X=(x1,x2,…,xm)和Y=(y1,y2,…,yn)，长度分别为m和n。其中xi与yj之间的距离dij采用欧式距离计算

dij=d(xi,yj)=|xi-yj|

(6)

计算得出两序列对应点间的距离矩阵D，并在D中确定出一条路径W=(w1,w2,…,wk)让X与Y匹配程度最大。为了求出有效路径，需要符合的约束条件见表2。

表2 约束条件

计算得出多条路径，其中最优路径为

(7)

综上所述，本模型的基本原理为，首先针对MFCC算法进行优化，然后结合PCA降维的梅尔频率倒谱(以下简称为“PMFCC算法”)，并组合DTW算法诊断出故障类型，简称为“PMFCC-DTW算法”。

3 轨道电路特征参数提取

本文将PMFCC特征提取过程分为两部分：梅尔频率系数和主成分分析。通过梅尔频率系数获取MFCC特征值后利用PCA进行降维处理，最终得到轨道电路特征参数。轨道电路特征提取流程见图5。

图5 轨道电路特征提取流程

选用图4中8种不同故障的信号进行MFCC特征提取，得到24维的MFCC信号特征，再进行PCA降维。通过求得各主成分φk的贡献率μk，计算出降维满意度。假如前k个主成分的累计贡献率δk大于阈值(通常为85%)，则选取前k个主成分作为新的样本主成分进行循环。其中，第k个主成分贡献率为

(8)

通过计算得出符合阈值的特征维数并不唯一，为更好地选出最有效的特征维数，本文利用费舍尔判别准则(Fisher准则)对满足累计贡献率δk>85%的特征参数直接进行二分类求解，其最优参数求解公式为

(9)

式中：Sa为类内散度矩阵；Sb为类间散度矩阵。

设d维度空间的两类样本为X1和X2，且样本个数为N，当d维度空间的样本映射到一维Y空间时得到y=wtx。其中，类内散度矩阵与类间散度矩阵分别为

(10)

(11)

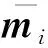
图6 Fisher准则分类正确率

从图6可以看出，8种故障的特征数据在不同维度下分类的正确性有很大不同。计算不同维数分类正确率的平均值，6维为78.54%、8维为87.39%、10维为81.19%、14维为78.22%、18维为74.09%，可以看出8维的分类正确率最高，随着维度增加或减少，特征数据的分类效果降低，差异性变小。因此，本文以8维数据作为信号特征。

进一步对降维后PMFCC算法得到的8维条件下信号特征与MFCC算法的24维信号特征进行比较分析，利用欧氏距离计算不同故障间的相对距离，通过距离的大小分析不同故障间的差异性。选定F1故障作为参考与F2～F8故障进行比较计算，然后归一化处理得到雷达图，见图7。

图7 F1作为参考的雷达图

从图7中可以看出，8维条件下PMFCC算法的特征数据差异性高于24维条件下MFCC算法，并且F1与F2～F8故障的相对距离较为均匀，不易受到外界干扰。同理，将F2～F8分别作为参考，计算得到的结果与图7类似。8维条件下的PMFCC特征数据间差别明显，为后续的模板训练和故障识别，既减少了计算量又降低了模板库的存储量，同时还将特征值进行最优化，不但提高了信号的识别精度也提高了信号的识别效率。

4 故障诊断模型

4.1 故障模板选取

本文利用DTW计算模板信号与测试信号在每一帧的Mel倒谱距离，通过该距离寻求待检测信号与模板信号的最佳匹配路径，从而实现测试信号与模板信号间的时差失真最小、相似特征最大。诊断流程由增量式训练和匹配识别两个阶段组成，见图8。通过历史故障数据训练出最优的故障模板作为匹配依据，然后将实时故障数据提取特征后与故障模板进行匹配，并将结果在人工复合后作为新的历史数据反馈给故障模式库进行训练形成新的故障模板，从而实现自适应效果。

图8 诊断流程

在实际运用中，增量式的故障模板库能够有效更新报告设备故障情况，提高诊断精准度，因此模板库的选取意义重大。本文使用K-means聚类与最小欧式距离结合的方式找出最优的不同故障的模板库，并且根据实时数据与故障模板进行对比后反馈给故障模式库进行训练形成新的各类故障，从而保证算法实际应用的有效性。K-means聚类主要步骤如下：

Step1输入故障集{X}，有n个样本和k个故障模式,分类{Gi，i=1,2,…,K}。

Step2随机选取k个初始聚类中心{c1,c2,…,ck}，依次计算故障集{X}到聚类核心的距离D(xi,cj)，按照最小距离原则形成k个聚类核心，计算式为

Dij=‖xi-cj‖i=1,2,…,nj=1,2,…,k

(12)

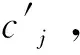
(13)

式中：Nj为第j个聚类中心的样本个数。

Step4利用式(14)～式(15)聚类准则数值E判断聚类结果是否合理，若合理迭代终止，否则重复Step2和Step3。

(14)

|E′-E|<ζ

(15)

4.2 结果分析

从采集的故障文件中随机抽取数据63条，其中发送端数据7条，防雷单元数据5条，电缆网络模拟数据9条，空心线圈断线数据6条，调谐单元短路数据10条，主轨出数据8条，小轨出数据7条，补偿电容断线数据11条。将随机抽取的数据使用K-means聚类得出各故障参考模板，再利用PMFCC-DTW故障诊断把t1～t9测试数据与F1～F8模式库中的参考样本进行匹配，求出部分动态匹配距离，见表3。其中匹配计算得到的数值越小，则距离越近，相似度就越高，并将该测试数据归为此类故障。例如表3中圈出的数据，t1所在列中最小的值是与F6相对应，故t1是F6故障；t4所在列中最小的值是与F1相对应，故t4是F1故障。同理，按此计算也可以得到动态匹配结果。

表3 部分动态匹配距离

为了证明本文采用的PMFCC-DTW算法进行故障诊断的有效性，根据实测ZPW-2000轨道电路的数据建立数据库，选取2 400条数据，做改进效果对比实验分析。其中发送端数据、防雷单元数据、电缆网络模拟数据、空心线圈断线数据、调谐单元短路数据、补偿电容断线数据、主轨出数据和小轨出数据各300条。PMFCC-DTW模型与MFCC-DTW模型的诊断效果对比见表4。对比结果显示，PMFCC-DTW模型单个故障的识别率高达96.67%，而且对每一种故障的识别率都要高于MFCC-DTW模型，正确率有明显提升。

表4 故障识别率 %

另一方面利用混淆矩阵(Confusion Matrix)计算实际样本值和模型诊断值的正确率、精准率和召回率，并统计模型诊断耗时。

正确率为

(16)

精准率为

Precision=TP/(FP+TP)

(17)

召回率为

Recall=TP/(FN+TP)

(18)

式中：TP为样本的真实类别是某类故障，并且模型诊断的结果是同类故障的个数；FN为样本的真实类别是某类故障，但是模型将其诊断成为其他故障的个数；FP为样本的真实类别是正常，但是模型将其诊断成为故障的个数；TN为样本的真实类别是正常，并且模型诊断的结果也是正常的个数。

基于改进效果对比实验的2 400条数据以及1 000条正常数据，仿真了HHT-DBWT算法和SVM算法，并与本文改进的PMFCC-DTW算法进行对比分析，评价结果见表5。

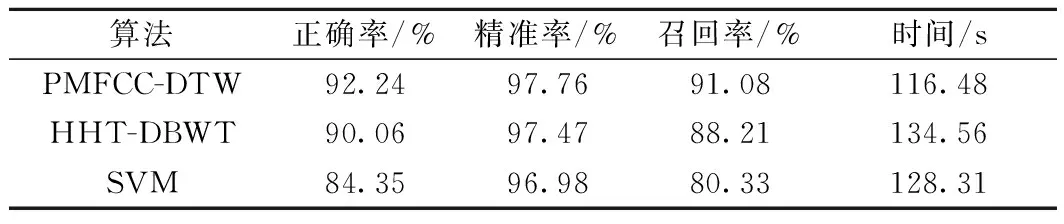
表5 评价结果

由表5可见，PMFCC-DTW算法的正确率较高，而且精准率高达97.76%，表示本模型诊断故障的准确度很高。通过召回率分析出模型诊断故障可信性强，且用时短。

在实际应用中，通过安装轨道电路室内外设备信号采集装置，结合信号集中监测系统获取室内外监测信息，利用本文方法对轨道电路信号实时监控实时诊断，若能获取较完整的监测数据和突发故障数据以便故障模式更深入研究，对提高轨道电路故障诊断及日常维护效率具有重要意义。

5 结论

(1)本文针对高速铁路轨道电路常见的故障，通过实地测试采集到的暂态电压数据按时域、频域进行智能化区段划分，利用MFCC提取出表征轨道电路状态的特征参数，并基于主成分分析进行特征降维，使用Fisher准则选出最优特征集，通过K-means聚类进行故障集训练，得到轨道电路暂态数据的初始模板，形成轨道电路的模板库，最后通过DTW模型计算出测试集与每种模型的匹配距离，从而进行故障诊断。

(2)通过实验以及与其他诊断方法进行对比可以发现，基于PMFCC-DTW的轨道电路故障诊断的识别时间大为缩短，正确率达到90%以上，为轨道电路设备健康状态监测提供了一种新思路。