结构准静态解耦载荷识别方法与结构随机载荷谱

孙晶晶，孙守光，王斌杰，马 爽，张亚禹，李 强

(北京交通大学 机械与电子控制工程学院, 北京 100044)

载荷谱是进行结构可靠性设计和可靠性试验验证的基础。建立载荷谱的前提是获取结构在实际运用条件下的完整载荷历程。工程结构运用载荷历程的获取，一般是通过测量载荷在结构上产生的响应进行反求，称之为载荷识别问题[1]。这方面的研究工作较早始于航空领域[2]，后来逐步扩展至航天、车辆、船舶、海洋平台等研究领域[3-9]。

载荷识别问题属于结构动力学中的反问题，这类问题解决起来通常要比结构动力学中的正问题更为复杂[1,9]。载荷识别方法广义上分为频域法和时域法[10]。经过四十余年的发展，已建立起直接求逆方法、正则化方法、小波分析法、遗传算法、逆虚拟激励法和神经网络算法等多种方法[1,3,11-14]。这些方法总体上还属于探索性的，成功应用于获取工程结构运用载荷历程的案例还有限[1,9-10,15]。

载荷识别问题解决起来更为困难的主要原因在于必须对载荷响应传递矩阵进行求逆运算。识别误差过大常常导致载荷识别失败，其根源在于载荷响应传递矩阵往往具有病态特性，求逆过程中会导致严重的误差放大[16-18]。

本文以转向架构架这一轨道车辆结构中可靠性问题最为突出的典型结构为对象，研究构架在实际运用条件下的载荷识别问题。结合构架实际运用情况下的动态特性分析，针对载荷响应传递矩阵的病态特性控制和矩阵求逆过程中的误差控制问题，探索针对性的解决方案。在此基础上，进一步研究确立构架基本载荷系。结合构架运用载荷历程的获取和构架基本载荷系的确立，可为建立构架随机载荷谱创造充分条件。

1 载荷识别方法的基本原理

对于任一结构的载荷识别问题，载荷与响应之间的传递关系均可以表示为

ε(ω)=H(ω)F(ω)

(1)

式中:ε(ω)为响应向量;F(ω)为载荷向量;H(ω) 为载荷响应传递矩阵;ω为向量和矩阵元素的载荷频率。

在实际测试响应时，总会产生测量误差，由上式求解后，产生的载荷误差可以通过下式估计[16-19]

(2)

式中:‖F‖为载荷向量范数;‖δF‖为载荷误差向量范数;‖ε‖为响应向量范数;‖δε‖为响应误差向量范数;cond(H)为传递矩阵的条件数，可以表示为

(3)

其中，λmax和λmin分别为传递矩阵的最大特征值和最小特征值。显然传递矩阵的条件数不小于1。

综合式(2)和式(3)可知，通过式(1)求解载荷时，产生的载荷相对误差一般会得到放大。实际上，大量的载荷识别案例表明，当传递矩阵条件数很大时，载荷识别会产生无法接受的误差。载荷识别过程中，通常情况下传递矩阵的条件数难于时时把握和控制，这使得载荷识别误差的控制也难以有效，成为导致载荷识别失败的主要原因[1,9-10,15]。如何在载荷识别过程中，可靠控制传递矩阵的条件数不至于过大是保证载荷识别取得成功的关键因素。

对于转向架构架而言，由于置于一系悬挂之上，构架动载荷与动应变响应主要集中在10 Hz以下频段[20-22]，而构架弹性模态的第一阶固有频率通常在30 Hz左右[23-25]；在载荷识别的范畴中，构架动载荷识别基本上属于低频范围。目前大部分的动载荷识别方法基本上是针对中、高频动载荷的，却很难准确识别出低频范围的动载荷[9]。鉴于构架动载荷的低频特征和动载荷识别方法的发展现状，本研究尝试采用准静态标定方法来确定构架传递矩阵，并以构架动应变响应作为测试响应，此时式(1)可以表示为

ε=KP

(4)

式中：ε为构架动应变响应向量；P为构架动载荷向量；K为构架载荷应变传递矩阵，在准静态标定方式下，K为常数矩阵。

为实现对传递矩阵K的条件数的可靠把控，有效抑制载荷识别误差，本研究采用解耦方法标定构架传递矩阵，通过最大限度地消除应变响应中载荷之间的相互影响，使传递矩阵K实现准对角化。当传递矩阵中非对角元素远小于对角元素时，对角线上的元素可以作为传递矩阵K的特征值的可靠估计，进而通过式(3)能够可靠估计传递矩阵K的条件数。因此，当采用解耦方法标定构架传递矩阵时，可以方便地确定传递矩阵的条件数，通过标定方案的适当调整可以实现对于条件数的有效把控，确保传递矩阵具备良好特性，进而有效控制载荷识别误差。此外，传递矩阵求逆过程是载荷识别产生误差的主要环节，当传递矩阵高度实现对角化后，矩阵求逆的大量运算可以省略，这也十分有利于减小载荷识别误差。

综上所述，消除载荷系之间的响应耦合，实现载荷系解耦的原则应包括两点：①载荷响应传递矩阵实现准对角化，即非对角元素远远小于对角元素；②载荷响应传递矩阵的条件数应尽量小。

2 构架载荷传递矩阵的解耦标定

以提速客车209P 转向架构架为研究对象。该构架承受的载荷有18个，分别为轮轨激扰产生的各轴端垂向载荷、横向载荷和纵向载荷(12个)，牵引产生的纵向载荷(2个)，制动时产生的制动吊座垂向载荷(4个)。各载荷作用位置及作用方式见图1。

图1 构架载荷示意图

2.1 构架基本载荷系

在实际运用过程中，转向架构架承受的载荷与构架的基本运动方式和运用方式相适应，以若干组相对独立的方式成组作用于构架，每一载荷组合均以自平衡方式呈现，这些载荷组合称之为构架基本载荷系。构架的基本运动方式主要包括浮沉、侧滚、扭转、横移、菱形等，基本运用方式主要包括牵引、制动等。每种基本运动和运用方式所对应的构架基本载荷系由UIC 515-4—2003[26]和BS EN 13749—2011[27]等国际规范详细描述，分别为浮沉载荷系Fv、侧滚载荷系Fr、扭转载荷系Fw、横向载荷系Ft、菱形载荷系Fo、纵向牵引载荷系Fl和制动载荷系Fb，见图2。

图2 构架各基本载荷系示意

在北京交通大学结构强度实验室多年开展构架载荷测试研究[28-29]的基础上，依据构架的运动特征，构架上还有可能存在现行国际规范中尚不包含的蛇行载荷系Fa，构架蛇行载荷系示意见图3。图3中，py1～py2为蛇行载荷，pRx1～pRx4为蛇行载荷反作用力。本研究将通过测试蛇行载荷系和对比分析由该载荷系产生的损伤情况，来判断是否有必要将该载荷系增加到构架基本载荷系中。

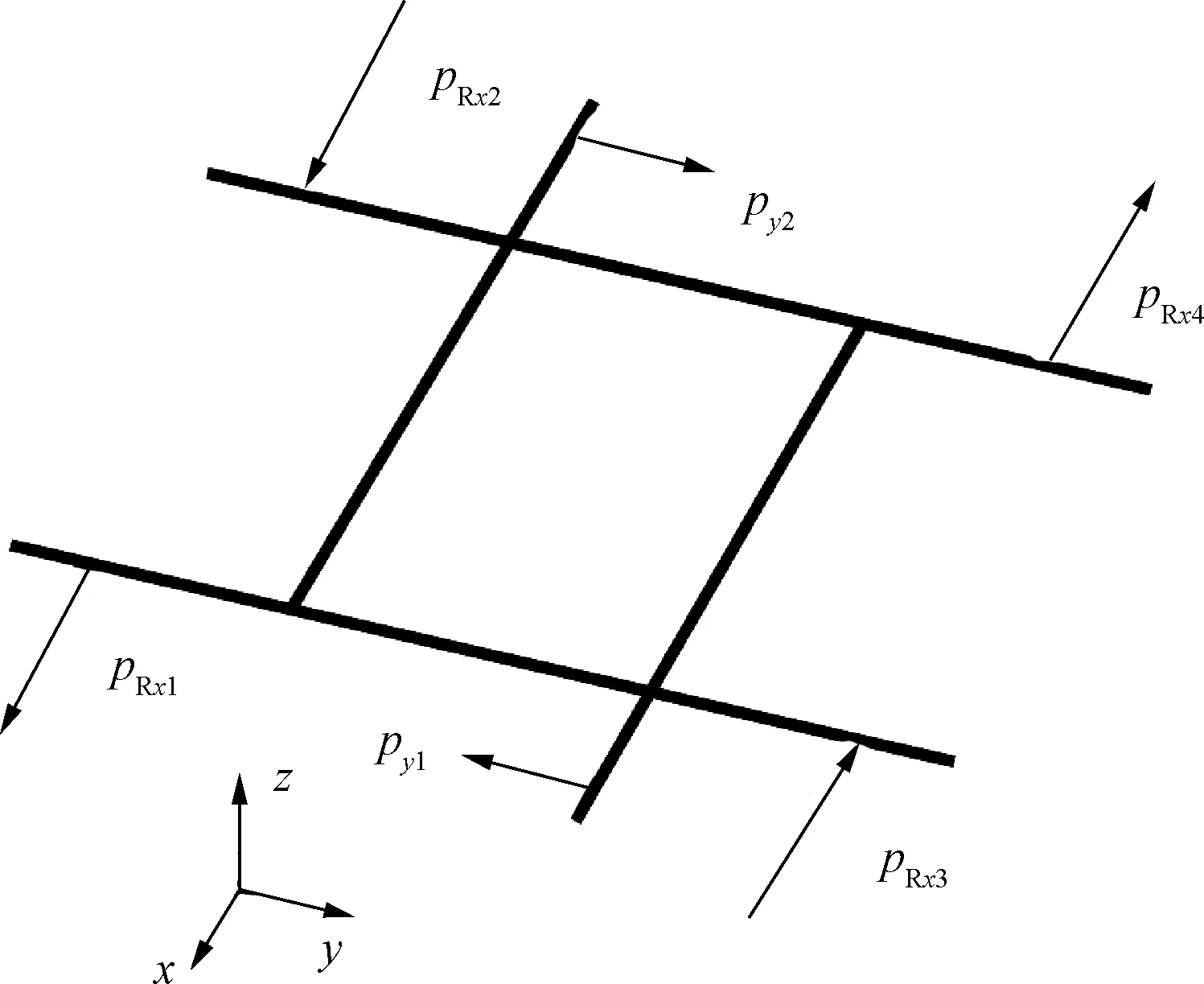
图3 构架蛇行载荷系示意图

2.2 构架基本载荷系的解耦标定

构架载荷以具有自平衡特征的基本载荷系方式成组出现。相应地构架的载荷解耦传递矩阵标定也是以基本载荷系为对象开展的。

在具体标定过程中，将构架基本载荷系分成2组：一组为浮沉载荷系、侧滚载荷系、扭转载荷系、横向载荷系、菱形载荷系和制动载荷系，以构架应变响应作为测试响应，通过构架标定载荷应变传递系数；另一组为纵向牵引载荷系和蛇行载荷系，以牵引拉杆应变响应作为测试响应，通过牵引拉杆标定载荷应变传递系数。

构架基本载荷系的解耦标定是一项十分细腻的工作。首先要对各基本载荷系在构架上产生的应变分布特性进行有限元分析，确定与每一基本载荷系对应的强响应区和弱响应区，并分析其应变分布具有的对称性特征。在确定某一基本载荷系的解耦测量方案时，测点区域选取方面一般优先考虑该基本载荷系对应的强响应区，最好同时又属于其他基本载荷系对应的弱响应区；测点应变组合选取方面则主要利用各基本载荷系产生的应变分布的对称性特征，必要时可进一步利用同一测点相互垂直方向上的应变通常符号相反的特点。构架各基本载荷系之间具有相对独立性，各自产生的应变分布情况和对称性特征差异显著，实践表明按上述方式确定构架基本载荷系的解耦测量方案是可行的。要获得构架基本载荷系之间比较理想的解耦效果，还必须对选定测点区域的测点应变组合进行优化，这需要对测点应变组合进行大量、细致的比选。

在解耦标定过程中，为了有效控制构架基本载荷系传递矩阵可能出现的病态状况，还需要对各基本载荷系对于各自测点应变组合的传递系数进行比较，实时估计传递矩阵的条件数，必要时调整解耦标定方案。

下面介绍2个典型的构架基本载荷系的解耦标定情况，分别是构架浮沉载荷系和菱形载荷系，其中浮沉载荷系的解耦实现相对容易，而菱形载荷系的解耦实现则相对困难。构架浮沉载荷系和菱形载荷系的解耦标定见表1、表2。

表1 构架浮沉载荷系的解耦标定

表2 构架菱形载荷系的解耦标定

由表1和表2可见：对于选定的构架浮沉载荷系优化测点应变组合，与构架浮沉载荷系自身影响相比，其他基本载荷系的影响不超过6%；对于选定的构架菱形载荷系优化测点应变组合，与构架菱形载荷系自身影响相比，其他基本载荷系的影响不超过2%。总体来看，解耦标定后的构架基本载荷系传递矩阵的非对角元素与对角元素相比，在量值上小两个数量级，比较好地实现了构架基本载荷系传递矩阵解耦。

解耦标定后，构架基本载荷系相对于各自测点应变组合的传递系数，居于构架基本载荷系传递矩阵的对角线上，见表3。由于该传递矩阵已实现高度解耦，这些对角线元素可以作为构架基本载荷系传递矩阵特征值的可靠估计。对于采用构架应变作为测试响应的基本载荷系，最大特征值对应菱形载荷系，最小特征值对应制动载荷系，作为相应传递矩阵条件数的良好估值，两者之比仅为3.6，显示出基于构架测试的基本载荷系传递矩阵状态优良。对于采用牵引拉杆应变作为测试响应的基本载荷系，两者对应的特征值相同，条件数估值为1，显示出基于拉杆测试的基本载荷系传递矩阵处于最佳状态。

表3 构架基本载荷系与各自测点应变组合的传递系数 10-6·kN-1

综合上述，本研究比较好地实现了构架基本载荷系传递矩阵解耦，获得的传递矩阵状态优良，能够有效控制传递矩阵求逆产生的误差，为开展构架载荷识别工作奠定了坚实的基础。

3 试验验证

开展构架运用载荷识别的目标是建立构架载荷谱，进而服务于构架定量化可靠性设计、提升和试验验证。要实现这一目标，识别出的构架运用载荷必须能够正确再现构架的运用损伤，这是检验构架载荷识别是否成功的根本标准。构架的运用损伤直接取决于构架在运用过程中所承受的动应力历程，可由对应运用里程的等效动应力来度量，具体计算方法详见文献[30-31]。因此，识别出的构架运用载荷能否正确再现相同运用区段对应的动应力，特别是整个运用过程对应的等效动应力，就成为检验构架载荷识别是否成功的直接标准。要进行上述对比，需要开展两项工作：①在实验室内标定构架基本载荷系与构架关键部位应力(或应变)之间的传递关系;②同时测试构架载荷和这些关键部位的动应力。

3.1 构架载荷应变传递关系

在构架上选取典型测点，①覆盖构架疲劳控制部位，②充分体现与构架所有基本载荷系的关联性。本研究共选取了56个典型测点，其中D1～D24测点为构架侧梁区域，D25～D44测点为构架横侧梁连接区域, D45～D48测点为构架牵引座区, D49～D56测点为构架制动座区，具体见图4。

图4 构架应变典型测点示意

采用类似于构架运用状态的约束方式，按照与构架各基本载荷系对应的加载方式，分别对构架分级施加载荷，在确认构架约束状况和载荷接触区域稳定后，测试构架典型测点的应变，计算出构架基本载荷系与典型测点应变之间的传递系数，具体见表4。

表4 构架基本载荷系与典型测点应变之间的传递系数 10-6·kN-1

3.2 线路试验简介

提速客车209P转向架构架于2015-10-13—2015-10-19，在大连至赤峰区段实际运用条件下进行测试。经运用部门确认，该线路路况较一般线路恶劣，具备典型性，适合于构架运用可靠性考核。测试共包含3个往返，累计运行里程5 826 km，累计运行时长近96 h。

构架测滚载荷系和菱形载荷系的测试情况见图5。构架典型测点的动应力测试情况见图6。限于数据量的庞大，为较清楚地显示工况特征，图中仅展示了时长600 s典型工况的测试结果。

图5 构架基本载荷系典型工况时域图

图6 构架典型测点实测动应力时域图

3.3 构架载荷识别分析评价

前已说明，对于构架载荷识别的效果，应当以能否正确再现构架等效动应力来评价。为此，首先需要采用线路实测获得的构架各基本载荷系的时间历程，借助构架各基本载荷系与构架典型测点应变传递系数，通过叠加各基本载荷系产生的动应力响应，来预测构架典型测点动应力的时间历程。

构架代表性测点实测动应力和载荷预测动应力在典型工况下的时间历程见图7。由图7可见，预测动应力与实测动应力相比，大小相近，变化趋势基本一致。上述测点与一个完整测试往返相对应的实测动应力和预测动应力的频谱图见图8。从图8中可以看出：实测动应力频域响应主要集中在10 Hz以下；采用实测构架载荷预测的动应力与实测动应力的频谱变化趋势基本相同，总体吻合良好。

图7 构架典型测点实测动应力与预测动应力的时域对比情况

图8 构架测点预测动应力与实测动应力频谱图

检验构架载荷识别成效的综合性标准，也是更具根本性的标准，在于实测构架载荷预测的等效动应力与实测等效动应力是否一致。本文中，各类等效动应力均对应于设计寿命里程(全寿命运用里程)，实测载荷预测的动应力和实测动应力均扩展至全寿命运用里程进行等效。对于209P转向架构架，全寿命运用里程取1 200万km。构架关键测点实测载荷预测等效动应力与实测等效动应力之间的比较情况见图9。由图9可见，对于构架上所有的关键测点，预测等效动应力与实测等效动应力的比值均在0.8～1.3之间，误差不超过30%。

图9 构架关键测点载荷预测等效动应力与实测等效动应力之比

为更进一步评价构架实测载荷的效果，图10还给出了构架可靠性设计现行国际规范对应的用于可靠性设计评价的应力幅(等价于本文中的等效动应力)与构架实测等效动应力的比较情况。由图10可见，构架可靠性设计现行国际规范给出的应力幅与实测等效动应力的比值在1.3～4.0 之间，误差可高达400%。按本研究实测构架载荷预测的等效动应力，比国际现行规范给出的等效动应力精度提高一个数量级。

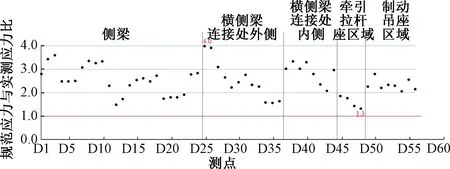
图10 构架现行国际规范等效动应力与实测等效动应力之比

根据文献[30]，运用寿命与等效动应力之间存在如下关系

(5)

式中：Dp为基于实测载荷预测的运用寿命；Dm为基于实测动应力预测的运用寿命；σp为实测载荷预测的等效动应力；σm为实测等效动应力；m为S-N曲线斜率，对于209P转向架焊接构架，m取值为3.5。

根据式(5)可知，本研究基于实测载荷预测的运用寿命与基于实测动应力预测的运用寿命的比值在0.46～2.5倍之间，预测精度基本满足定量预测构架运用寿命需要，可用于既有构架可靠性提升；而基于现行国际规范载荷预测的运用寿命与基于实测动应力预测的运用寿命的比值在2.5～128倍之间，表明构架可靠性设计现行国际规范还处于定性层面，不适合定量预测构架运用寿命。

上述比较显示：对于载荷响应主要集中于低频区域的转向架构架，采用本研究建立的结构准静态解耦载荷识别方法，获得的构架载荷识别结果可以比较好地预测构架运用等效动应力，也即构架运用损伤情况，已能够满足既有构架可靠性提升需要。从适应构架可靠性设计要求这一根本目标来看，本研究开展的构架载荷识别工作是相当成功的。

4 构架随机载荷谱

建立构架随机载荷谱需要两方面条件：①确立构架完备的基本载荷系；②获取构架实际运用条件下各基本载荷系具有代表性的载荷时间历程。

在构架基本载荷系的确立方面，在构架可靠性设计现行国际规范的基础上，补充了蛇行载荷系。构架各测点与蛇行载荷系对应的等效动应力同全部基本载荷系对应等效动应力的对比见图11。由图11可见，在构架牵引拉杆座区域，蛇行载荷系对等效动应力有显著影响；对于其他区域则影响不大；总的来看，增加蛇行载荷系是有意义的。

图11 蛇行载荷系对构架关键测点预测等效动应力的响应比

由图9可知，基于本研究确立的8个构架基本载荷系及其实测运用载荷时间历程，可以比较高的精度预测构架运用等效动应力；一方面表明这8个基本载荷系对于拖车构架具有完备性；另一方面也表明结合这些基本载荷系的运用载荷时间历程，可以直接建立构架随机载荷谱。

随机载荷谱是最接近于实际运用条件的载荷谱，应用时全部基本载荷系同步施加于构架之上，每个基本载荷系对应着各自的载荷时间历程。

当应用于构架可靠性设计或者构架可靠性试验验证时，随机载荷谱还不够方便，对试验设备的要求也往往过高，实际应用时一般还需要在此基础上编制出方便应用的载荷谱。

5 讨论

在应用本研究建立的结构准静态解耦载荷识别方法时，载荷传递矩阵的解耦标定过程至关重要，需要把控好每一个关键细节。由图8可知，在5 Hz以下的低频区域，构架关键测点动应力的载荷预测结果与实测结果还存在较为明显的偏差。具体来看，测点14的预测结果大于实测值，而测点31的预测结果则小于实测值。不仅两者的偏离趋势不同，而且在低频区域偏差更为显著，也与准静态识别方法的基本原理相抵触。经过细致地分析整个测试过程，认为问题的主要原因在于：在标定过程中，对于构架的约束处理还不够到位，特别是在侧滚载荷系和扭转载荷系的标定过程中，垂向约束刚度显著大于构架运用时的垂向在位刚度，这对于构架横侧梁连接区域的载荷响应传递关系可以产生较为明显的影响。

对于城市轨道车辆和高速动车组，构架动应力测试情况显示，构架的1～2个弹性模态可能被有效激发[21,29,32-33]。对于弹性模态能够被有效激发的构架，载荷识别时应在本研究建立的结构准静态解耦载荷识别方法的基础上，进一步考虑弹性模态的动态放大效应。就构架而言，激发出的弹性模态一般呈明显分离状态，可以在某一模态频率附近频段，按单自由度方式识别模态参数，进而计算并消除弹性模态的动态放大效应。

6 结论

本研究在分析结构载荷识别误差产生机理的基础上，针对低频响应结构，建立了结构准静态解耦载荷识别方法，通过确保载荷响应传递矩阵的良性状态和省略传递矩阵主要的求逆运算过程来控制载荷识别误差。采用提速客车转向架构架进行了测试验证，结果表明本研究建立的载荷识别方法可以有效控制长周期服役条件下的载荷识别误差，成功解决了现有结构载荷识别方法不适用于低频响应结构载荷识别的问题。

在构架可靠性设计现行国际规范的基础上，补充确立了蛇行载荷系，完善了拖车构架基本载荷系，进一步结合构架各基本载荷系的实测运用载荷时间历程，可建立构架随机载荷谱。依据实测载荷预测的构架等效动应力与实测等效动应力相比，误差不超过30%，运用寿命预测误差不超过2.5倍；比构架可靠性设计现行国际规范预测的等效动应力精度提高一个数量级，运用寿命预测精度提高2个数量级。运用上述体系建立的载荷谱，适用于对既有构架进行可靠性升级，并具备将现有国际规范由定性层次提升至定量层次的潜力。