考虑低行动力人群的公交线网优化设计

贾庆林，晋民杰，张 涛，孙 帆

(太原科技大学 交通与物流学院，太原 030024)

公交出行对于人们参与社会活动起着非常重要的作用，然而我国很多人由于行动力的原因，无法获得良好的公交出行服务，这些人通常被称为低行动力人群，包括老年人群、残疾人群和低收入人群.他们由于不能自由地选择出发地点、时间以及目的地，而常常被城市公交系统边缘化.

截止到2018年，我国60周岁及以上人口达24 949万人，占总人口的17.9%，随着我国步入老龄化社会，老年人已成为公交出行的重要服务对象.据滴滴公司发布的《2016年老年人出行习惯调查报告》显示，56.36%的被调查者出行主要依靠公交车.中国残疾人联合会发布的数据显示，75%以上的残疾人表示交通不便问题是其不愿意出门的重要原因.据2017年各地城镇就业社会平均工资表显示，目前我国有71%的人口属于低收入人群，受到自身经济条件的约束，低收入人群对交通服务价格的承受能力差(很少使用私家车和出租车)，一般选择公交出行.因此，开展公交线网优化对于低行动力人群的公交出行具有深远的意义.

近年来，国内外相关学者运用遗传算法在公交线网优化设计方面展开了大量的研究.FAN等在公交需求变化时，利用遗传算法系统地研究了公交线网优化设计问题，并通过算例来验证算法的性能[1]；NAYEEM等提出精英遗传算法求解公交网络优化设计模型，并寻求未满足服务和满足服务的总出行时间，用此建立满足模型要求的目标函数[2]；PTERNEA等为优化公交网络系统，提出满足用户成本、运行成本及环境成本的目标函数，并应用遗传算法对所提出的设计模型及函数进行求解[3]；孙志田等提出一种新型的公交线网优化设计模型，并构造满足算法求解应用的一系列前提条件和初始种群[4]；韦尚成提出以乘客最小乘车费用以及公交公司最小运营费用为目标的综合优化设计模型，并应用遗传算法进行求解[5].

基于上述研究成果，本文首先建立一种考虑低行动力人群的公交线网优化设计模型，并在此基础上应用遗传算法进行求解，然后使用MATLAB软件进行编程，最后通过算例研究，来验证该模型和算法的实效性和适用性.

1 公交线网优化设计模型

1.1 问题描述

公交线网优化主要研究城市线路规划和乘客出行成本，但在优化过程中，发现低行动力人群和普通大众之间在公交出行方面存在着博弈关系，为此，需要着重考虑低行动力人群的公交出行需求，就要求建立一种符合实际条件的数学模型.

本文是以某区域的低行动力人群和普通大众需求数据作为依据，以这2个群体所花费的最小出行时间为目标函数，以最大客流量、公交线路总长度为约束条件，并按照遗传算法进行求解.

1.2 模型假设

由于公交行驶环境会受不同路径、不同时段的影响，为使模型更具有适用性，本文做出以下假设[6-7]：

1) 各公交车为同一车型，且每辆公交车的客流量都是额定的、相同的；

2) 每条公交线路的首末站是已知的；

3) 公交资源有限，路段数量是恒定的.

1.3 模型建立

1.3.1 目标函数

模型需要考虑低行动力人群和普通大众公交出行选择权的博弈关系以及公交直达与未满足公交出行的博弈关系，参考REN和FAN的模型算法[8-10]，公交线网优化设计模型的目标函数如公式(1)～(8)所示.

1) 满足公交直达的时间成本：

(1)

(2)

(3)

(4)

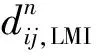
2) 未满足公交服务的时间成本：

(5)

(6)

(7)

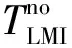
3)公交线网优化设计模型的目标函数：

(8)

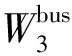
1.3.2 约束条件

在模型建立过程中，需要充分考虑公交线路运行长度以及1辆公交车的最大客流量，这就要求对它们进行约束，其约束条件如公式(9)～(10)所示：

Lmin≤Ln≤Lmax

(9)

(10)

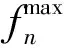
2 遗传算法应用

2.1 编码规则

公交线网可以由若干条公交线路组成，每条公交线路可由一定长度的整数字符串表示，编码规则如表1所示.

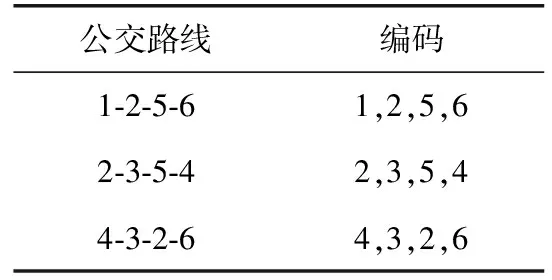
表1 编码规则

2.2 选择算子

根据适应度比例的选用原则，按照每一个种群的目标函数值的大小，来决定其是否保留.也就是说，将所有种群按照目标函数值，进行大小排序，采取一定的比例，把函数值优异的种群留下，去掉适应性较差的种群，选择规则如图1所示.

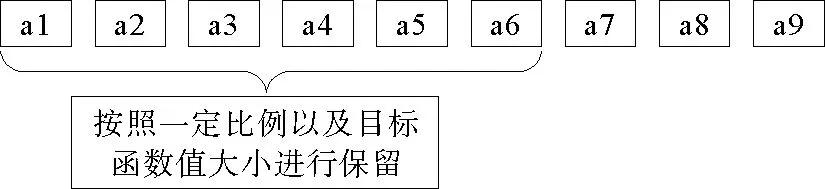
图1 选择算子规则

2.3 交叉算子

交叉算子可以分为整体单点交叉和局部双点交叉.其中，整体单点交叉是将公交线网的所有路径看成一个整体，从2个不同的父代线网方案，通过随机的单点交叉，形成2个不同的子代线网方案；局部双点交叉是对公交线网中的任意2条线路进行双点交叉，要求始末点不能更改以及交叉之后得到的2条子代必须是畅通路径[11]，交叉规则如图2、图3所示.

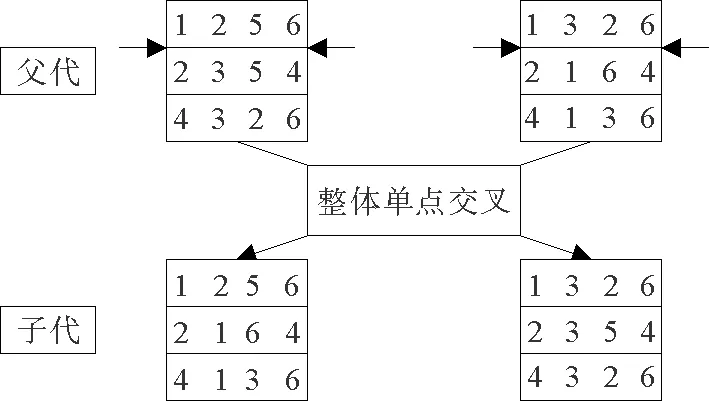
图2 整体单点交叉规则

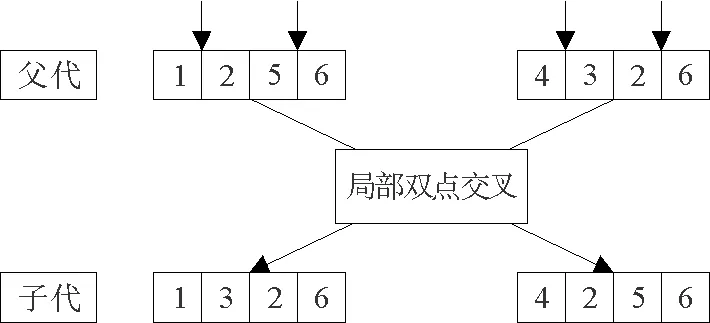
图3 局部双点交叉规则

2.4 变异算子

变异算子是采取一定范围内的随机数进行代替，要求始末点不能变异，变异后的线路必须畅通，变异规则如图4所示.

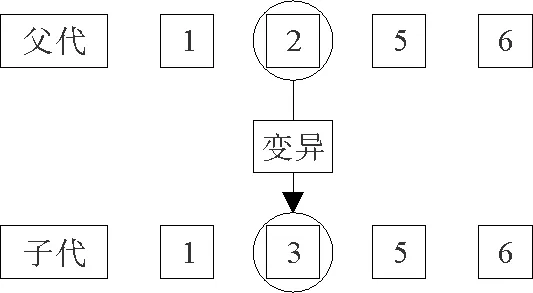
图4 变异规则

2.5 种群更新

种群更新是将3部分种群合并成整体，并按照目标函数值的大小进行排序，选择一定数量且适应性强的种群进行下一步迭代，其中，这3部分种群分别为选择、交叉、变异前的种群，选择、交叉、变异后的种群以及根据线路始末点随机生成的种群，其种群更新规则如图5所示.

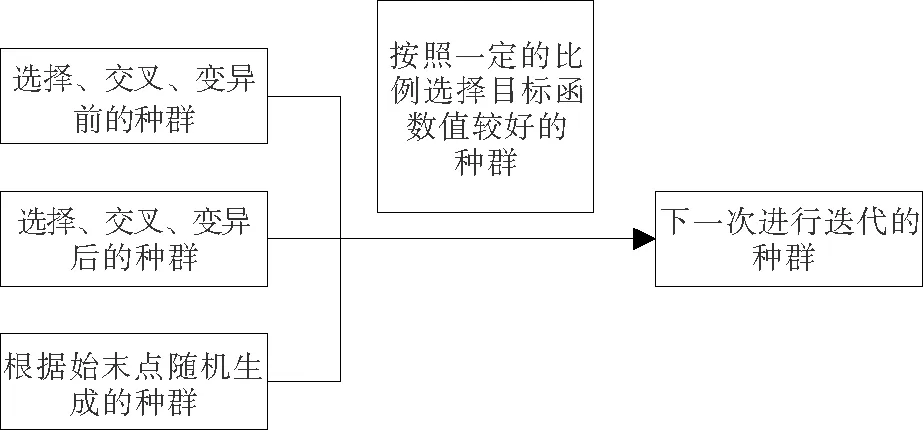
图5 种群更新规则

基于公交线网优化设计模型以及遗传算法应用，得到本文的求解流程，如图6所示.

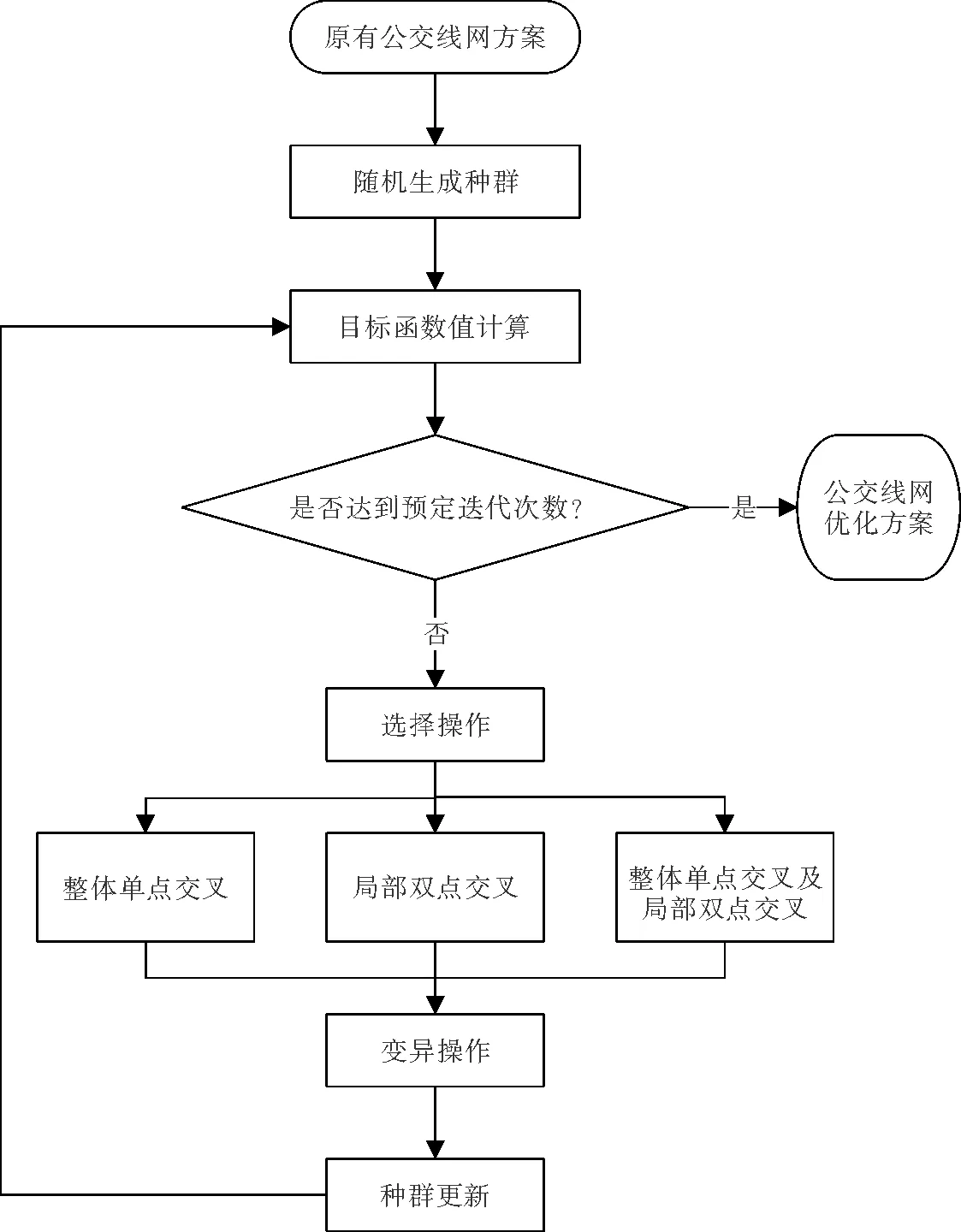
图6 公交线网求解流程

步骤1：根据原有的公交线网方案，可以得到一定数量的种群规模.

步骤2：设置参数，包括种群规模、交叉比率和变异比率，以及OD需求矩阵，站点间距矩阵和一系列求解目标函数值的相关参数.

步骤3：计算目标函数值，对每一个种群进行计算，并得到其适应度以及达到迭代次数后，输出优化后的公交线网方案.

经过该路段交通量数据调查发现在每天上午7～8点，下午4～5点这个时间段车流量较大且易发生交通堵塞，所以建议工程施工人员尽量避免在这个时间段施工作业，防止顶力过大及路基塌陷等事故。

步骤4：选择，按照目标函数值的大小，对所有种群进行排列，去掉适应度差的种群.

步骤5：交叉，选择操作后，将剩下的优异种群进行整体单点交叉和局部双点交叉.

步骤6：变异，对交叉后的种群，进行变异处理.

步骤7：种群更新，将3类种群(选择、交叉、变异前的种群，选择、交叉、变异后的种群以及根据线路始末点随机生成的种群)遵循模型的目标函数值，进行大小排序，选择适应性强的种群，进行下一步迭代，转至步骤3[12-13].

3 算例研究

结合上述公交线网优化设计模型和遗传算法应用，以公交线网为研究对象，进行仿真验证.通过实际公交客流情况和公交跟车调查，得到普通大众和低行动力人群的公交需求数据.该线网有8个节点和15个路段，公交车运行速度为30 km/h，公交线网运行如图7所示，假定的原始公交线路如表2所示.

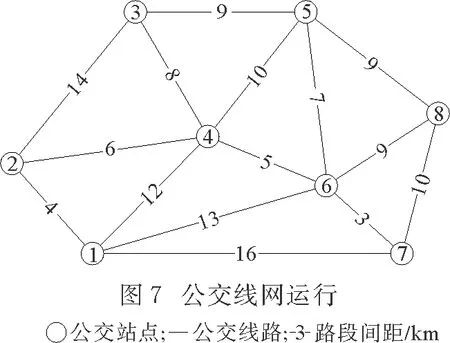
表2 原始公交线路

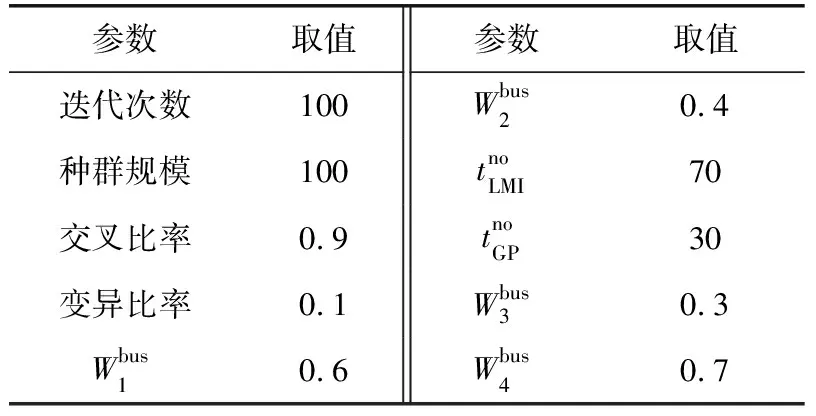
表3 主要参数设定

从表4中可以得知优化后的每条公交线路；表5显示出在公交直达需求方面，低行动力人群出行总时间的优化程度(优化17 h)小于普通大众出行总时间的优化程度(优化46 h)，但是在未满足公交需求方面，低行动力人群出行总时间的优化程度(优化1991 h)远远大于普通大众出行总时间的优化程度(优化1344 h)，综合这2个方面，可以得出低行动力人群的优化程度比普通大众的优化程度多了618 h，另外低行动力人群和普通大众的目标函数值由原来的12 140 h优化为9786 h；图8说明该遗传算法具有良好的收敛性.

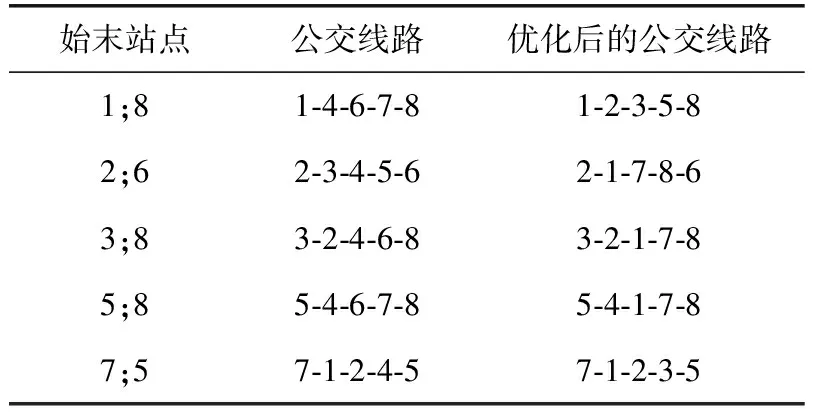
表4 公交线路优化

表5 公交线网优化 h

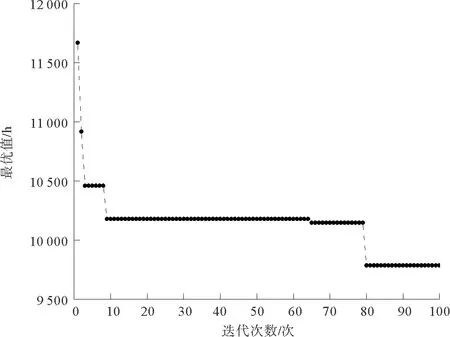
图8 优化过程迭代

4 结论

1) 本文是以公交运行线网为研究对象，运用网络建模理论、遗传算法相关知识以及充分考虑低行动力人群和普通大众在公交出行方面的博弈关系，并在原始公交线路与公交跟车调查的基础上，对公交线网进行优化，并与原始线网作对比.

2) 通过模型建立与遗传算法应用，将低行动力人群的直达需求出行总时间由583 h优化为566 h，未满足公交需求的出行总时间由7952 h优化为5961 h；普通大众的直达需求出行总时间由739 h优化为693 h，未满足公交需求的出行总时间由8825 h优化为7481 h；原始线网的目标函数值由12 140 h优化为9786 h，从中可以得出在公交出行时间成本方面，优化后的公交线网比原始的公交线网更加节约时间，另外低行动力人群的优化程度大于普通大众的优化程度.研究结果与实际公交需求相符，并验证了模型和求解算法的有效性和可行性，对公交公司制定公交线网优化时，充分考虑低行动力人群的公交出行有一定的参考价值.