水流荷载作用下海洋群桩受力特性研究
时 健,蒋宗南,孔德森,3,*
(1.山东科技大学 土木工程与建筑学院, 青岛 266590;2.北京中岩大地科技股份有限公司, 北京 100089;3.山东科技大学 山东省土木工程防灾减灾重点实验室, 青岛 266590)
近海风电基础多采用大直径单桩和群桩的形式,其中大直径单桩工艺成熟,使用广泛,但会有溜桩[1]等问题的存在,导致施工困难.而群桩虽然施工方便,但在海洋环境中的受力情况十分复杂,有上部风机自重荷载、结构自重荷载、风荷载、波浪荷载、水流荷载等,其中群桩的水流荷载由于其结构的特殊性,受力十分复杂.对于单桩结构在特定的雷诺数范围内,会在桩后产生左右两侧成对、交替出现、方向相反的漩涡,即卡门涡街现象[2].
在计算流体力学领域,针对圆柱绕流的研究,主要以雷诺数为控制参数,研究单圆柱的漩涡脱落情况[3-5].近年来,针对高雷诺数[6]和多圆柱绕流[7-9]的研究开始增多.现在,关于变截面圆柱绕流的研究[10]也逐渐展开.
但海洋环境中雷诺数都比较高,并且群桩的排列方式多种多样,水动力特性极为复杂,对于2×2群桩在海洋环境下的水流荷载受力特性研究并不深入.
程友良等[11]采用大涡模型,对雷诺数Re=3.5×106的情况下,对多个比转速的旋转圆柱绕流进行了数值模拟,并分析了圆柱的升、阻力系数和斯特劳哈尔数(St).结果表明,随着比转速的增大,桩柱的横向力逐渐增大,阻力系数也随之增大,而升力系数呈周期性减弱.
崔宜梁等[12]对串列双圆柱进行三维数值模拟,分析了双圆柱受到的平均阻力、升力,后柱周向压力以及斯特劳哈尔数等水动力特性.结果表明,在Re=20 000的串列双圆柱绕流中,两圆柱中心间距L与圆柱直径D的比值为4时,后柱受前柱尾流影响大.
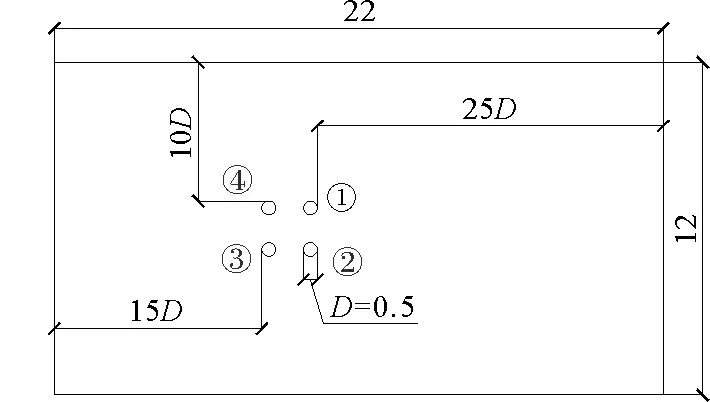
李聪洲等[13]采用改进的延迟分离漩涡方法模拟了高雷诺数下的桩体绕流,包括单圆柱、单方柱、串列双圆柱和串列双方柱四种情况,研究了不同雷诺数下圆柱与方柱的水动力特性.研究表明,单方柱绕流在2000 综上所述,为较好地反映群桩结构在海洋洋流荷载作用下的受力和振动特性,本文采用Fluent有限元软件,对海洋群桩进行建模和计算,分析各桩的升力系数和阻力系数的时程曲线以及桩周环向压力分布,以期得到海洋群桩受力分布规律和振动特性,对海洋工程中群桩基础的设计和优化提供参考. 海洋群桩的工程环境为四面广阔的流场,而数值模型无法完全模拟,因此模型假设流场为一维流场,从左侧进口边界流入,在右侧出口边界流出.同时,为了模拟真实的海洋环境,将上下边界设为对称边界.海洋群桩数值计算模型如图1所示. 图1 海洋群桩数值计算模型(单位:m) 目前,海洋石油钻井平台以及大型风电机组都已从浅海走向深海[14].在海洋平台的基础中,四桩导管架的应用很广泛,故进行四桩结构的模拟计算.桩直径D为0.5 m,桩间距为2D.为避免边界对流场产生影响,选择进口边界距前排桩15D,出口边界距后排桩25D,上下边界距离各侧桩10D.流场进出口总长22 m,上下边界相距12 m,桩长12 m.为便于分析,对各桩体进行编号,如图1所示.各桩对应的数据用桩体编号作为下标来区分. 流体运动需要遵守质量守恒定律.对于流场范围内任意选定的几何空间,单位时间内在此空间的流体质量保持守恒.因此,流体的速度及密度都是时间和空间坐标的函数,流体的运动属于不可压缩黏性流体的运动,其控制方程为连续性方程,即 (1) 式中:u,v,w为3个速度分量;ρ为流体密度,g/cm3. 湍流流动是一种高度非线性的复杂流动,处在湍流状态下的流体,流场的各种参数如水质点的速度、压力等都随时间与空间发生不规律的变化.针对湍流流动的特点,按产生漩涡的尺寸,将流场分为大尺寸漩涡和小尺寸漩涡. 大涡模型(LES)的基本思想是:大漩涡对流场的影响比较大,湍流扩散、质量、动量、能量等的变换和雷诺应力都是通过大漩涡实现的,而小漩涡主要起耗散作用.研究表明,在尺度足够小的情况下,几乎所有的漩涡都具有一定的相似性. 因此,将湍流中的大漩涡和小漩涡分开处理,大漩涡通过N-S方程直接求解计算,小漩涡通过亚格子模型建立与大漩涡之间的关系,对其进行模拟,而大小漩涡的区分是通过滤波函数进行的.目前较为常用的滤波函数主要有三种:盒式滤波函数、富式截断滤波函数和高斯滤波函数[15]. (2) 式中:V为计算单元的体积;x为滤波后的空间坐标;x′为实际流场中的空间坐标. 用此理论来解决不可压缩流体,过滤N-S方程,将得到以下方程[16]: (3) (4) 其中,亚格子尺度应力τij为 (5) 以上公式为N-S方程的张良表示法,其中u,v为速度分量;p为压力;上划线符号标记的量代表该量为时均值;系数i,j的取值范围为(1,2,3). 亚格子模型采用壁挂式本地涡黏度(WALE)模型[17].在Fluent中,默认的WALE常数Cω为0.325,研究表明将它用于流量范围跨度大的区域能取得准确的结果. 模型进口边界采用inlet属性,进口流速为1 m/s,进口压力为0 Pa;出口边界采用outflow属性;上下边界采用symmetry属性,用于模拟无限流域;桩边界采用wall属性,即无滑移固壁边界. 模型按照15 ℃时的海水属性赋值,流体选用液体密度为998.2 kg/m3,动力黏度为0.001 021 Pa·s. 模型的雷诺数[18]为 (6) 式中:U为来流速度;L为特征长度;μ为动力黏度. 斯特劳哈尔数为 (7) 漩涡的脱落频率f[19]为 (8) 漩涡的脱落周期t为 (9) 根据漩涡脱落周期,设置时间分析步为0.05 s,时长25 s. 采用ANSYS ICEM CFD软件对模型进行网格划分.将模型分为10个计算区域,从外到内逐渐加密,总体网格尺寸为0.2 m.由于流场模拟的雷诺数Re=488 834,为湍流流动,在采用大涡模型计算时要借助亚格子模型进行计算,故需要对桩附近的网格进行加密.加密区域分为内部区域和外部区域,外部区域宽度为2D,网格尺寸为0.05 m;内部区域宽度为1D,采用等比加密,第一层网格节点到桩体表面的距离为0.005 m,按1.076倍尺寸过渡.网格类型采用结构性网格,网格总数量为28 714.网格划分及桩附近网格加密如图2所示. 图2 网格划分及细部放大 检测网格质量的参数y+值的计算公式[20]如下: (10) (11) (12) 式中:Δy为第一层网格节点到壁面的距离;u*为近壁面摩擦速度;τω为壁面剪切应力;Cf为壁面摩擦系数. 根据计算,模型中各个壁面中y+值最大为197,壁面各网格点y+值随网格点距壁面上游边界最小值点顺流方向距离的分布规律如图3所示.研究表明,只要y+值在300以内,壁面函数就可以准确地计算出结果. 图3 壁面各网格点y+值分布 模拟结果的准确程度由参数的选取和网格质量两方面决定,而网格的质量又由网格的边界层划分、网格密度、光滑性以及单元类型决定.计算得到的升、阻力系数是否准确,漩涡的脱落和泄放是否能真实的模拟,很大程度上取决于网格质量的好坏.为了验证模型的参数选取和网格划分的准确性,以及与群桩模型做对比,建立了相同尺寸、相同参数的单桩模型,并采用试验对比和斯特劳哈尔数验算两种方法进行分析.单桩模型计算结果如图4所示. 图4 单桩阻力系数和升力系数时程曲线 对比算例采用了吴国雄教授Re=500圆柱绕流试验[21],试验结果如图5所示.由于试验无法实现与实际工程一样大小的足尺模型,所以试验环境下的雷诺数都相对较小.故采用文献[22]中的弗劳德相似原理进行缩尺对比.计算结果表明,单桩模型结果与吴国雄教授试验结果基本一致. 图5 单圆柱绕流水动力系数试验结果[21] 斯特劳哈尔数(St)是研究圆柱绕流的一个重要特征参数,可以衡量数值模拟结果准确性,是流体力学中相似准数的一个,为量纲为1常数[23]. 斯特劳哈尔数的计算式为 (13) 式中:fs为漩涡脱落频率. 如前文所述,稳定后升力系数的频率即该桩漩涡脱落的频率.因此,将桩体的升力系数曲线进行快速傅里叶变换(FFT),生成功率谱密度分布,如图6所示. 由图6可以看出,1号桩与2号桩升力系数功率谱密度都在0.404 Hz时达到峰值.将漩涡脱落频率fs=0.404 Hz代入式(13),得到斯特劳哈尔数为0.202,与式(11)计算结果相近,说明数值模拟结果有效. 流体运动时对细长结构物的作用力主要有沿流向的阻力和垂直流向的升力. 当流体接近物体前缘时,流动受到阻碍而产生压力,并且随着流动,这个压力会沿物体表面转移到后方.但当Re数较大时,这一压力会在物体截面最宽点产生分离,分离点即为物体表面流速从正到负的变速点,在分离点后面沿物体表面倒流,产生漩涡. 漩涡在桩体两侧交替产生和脱落,当桩体一侧产生漩涡时,该侧流速小于另一侧,产生压力差,也就是升力(FL).此漩涡脱落的同时,另一侧漩涡也在产生,升力就因此改变方向.因此,漩涡脱落的周期就是升力时程曲线的周期,即升力周期.与地震荷载不同[24],水流荷载通常是具有规则性的. 与此同时,漩涡的脱落会在桩体后面产生低压区,与桩体前部流体产生压力差,即阻力(FD).当漩涡脱落以后,低压区压力变大,阻力变小.阻力周期为升力周期的一半,即每个漩涡的产生和脱落,都会构成阻力系数的一个周期. 圆柱绕流过程中,桩受到来流方向平行和垂直的力,分别为阻力(FD)和升力(FL).其计算公式[25]为 (14) (15) 式中:CD为阻力系数;CL为升力系数;U为无穷远处的流速,m/s;D为桩径,m. 在阻力和升力的计算公式中,密度、流速和桩径都是定值,因此,阻力系数和升力系数的变化,即阻力和升力的变化.并且阻力系数和升力系数都是量纲为1系数,对桩的受力有代表性. 从图7和图8中各桩的阻力和升力时程曲线的对比中可以发现,1号桩和3号桩,即前排桩的受力相近;2号桩和4号桩的受力相近.说明2×2群桩中,面对来流方向的两列桩会发生几乎等效的相互影响.图9所展示的涡量也很好地印证了这一点. 图9 涡量等值线(t=25 s) 以1号和2号桩为例,对比分析群桩中各桩受力的不同. 1号桩的阻力系数稳定后维持在1.0~2.0,而2号桩阻力系数稳定后在-0.5~2.0,两者到达波峰与波谷的时刻接近. 1号桩的阻力系数时程曲线十分具有代表性,其工况与单桩受力(图4(a))相似.但2号桩的曲线与单桩的受力状态很不一样,其曲线的上限值与1号桩接近,但其稳定后的下限值却远低于1.0,甚至为负数,即阻力改变了方向.结合涡量等值线图(图9)分析可知,造成这一现象的原因在于1号桩后脱落的漩涡泄放至2号桩前时,会产生低压区,其压力甚至低于2号桩后产生的低压区,故使2号桩曲线稳定后的下限值低于1号桩,甚至产生方向向前的阻力. 1号桩的升力系数稳定后以CL=0为对称轴,上下对称波动,幅值为1.5左右,与图4(b)所示的单桩升力系数曲线比较接近,只是达到漩涡稳定释放的时间,群桩要比单桩短;2号桩的升力系数稳定后以CL=0为对称轴,上下对称波动,幅值为3左右,两者每次达到峰值的时间接近,波峰与波谷的位置也相近. 但2号桩的升力系数时程曲线每一个波峰的峰值都不相同,图8(b)中t取25 s并不能完全揭示该现象的全貌,故取t=100 s进行计算,计算结果如图10所示. 从图10中可以看出,1号桩的升力系数时程曲线相对稳定,但2号桩曲线中各个峰值的大小波动较大,且上升周期与下降周期均不确定,只呈现出大致的波动趋势,但其趋势与1号桩曲线的峰值波动趋势类似.同时,图10还呈现出另一个现象,即2号桩所受的升力,负向峰值大于正向峰值,说明1号桩产生的漩涡大多经过2号桩的同一侧,因此会减小2号桩该侧的压力,从而增大指向该侧的升力. 取24.4 s时,即1号桩升力系数CL1=0和单桩CL=0时,桩周环向的绝对压力(取参考压力为大气压101 325 Pa)如图11所示. 由图11可知,1号桩与单桩的桩周压力的趋势和数值都比较接近,大致呈现出沿0~180°线上下对称,但1号桩明显呈现出内侧压力大于外侧的情况,经分析是由于群桩对流体的阻碍,降低了群桩范围内的流体速度,增大了压力,因此1号桩内侧压力大于外侧. 相比较1号桩,2号桩的桩周压力分布却有很大的不同.2号桩的曲线也呈现出了内侧压力大于外侧的规律,但峰值并没出现在桩前(0°)和桩后(180°)的位置,而是出现在了桩前内测(300°)的位置,即表现出了峰值的滞后性,这一点与在图9中所表现出的特征相互印证. 1) 2×2群桩中,上下两排桩的受力是上下对称的,发生干扰的效果也是相互的. 2) 群桩中后排桩会受到前排桩所释放的漩涡的影响,主要表现在后排桩漩涡释放稳定后,阻力系数时程曲线的波谷极值对比前排桩有极大的降低,甚至出现负值,但波峰极值却几乎没有影响. 3) 后排桩的升力系数对比前排桩,所受的升力波峰峰值不稳定,主要表现在2号桩的升力系数曲线波谷极值相比于1号桩增大了接近一倍. 4) 分析了群桩中各桩的桩周环向压力,并与单桩进行对比,发现群桩的存在使其范围内的流体流速降低,压力增大,因此各桩会受到由群桩内部向外的压力.1 数值计算模型的建立
1.1 模型尺寸
1.2 控制方程
1.3 湍流模型
1.4 初始条件与材料属性
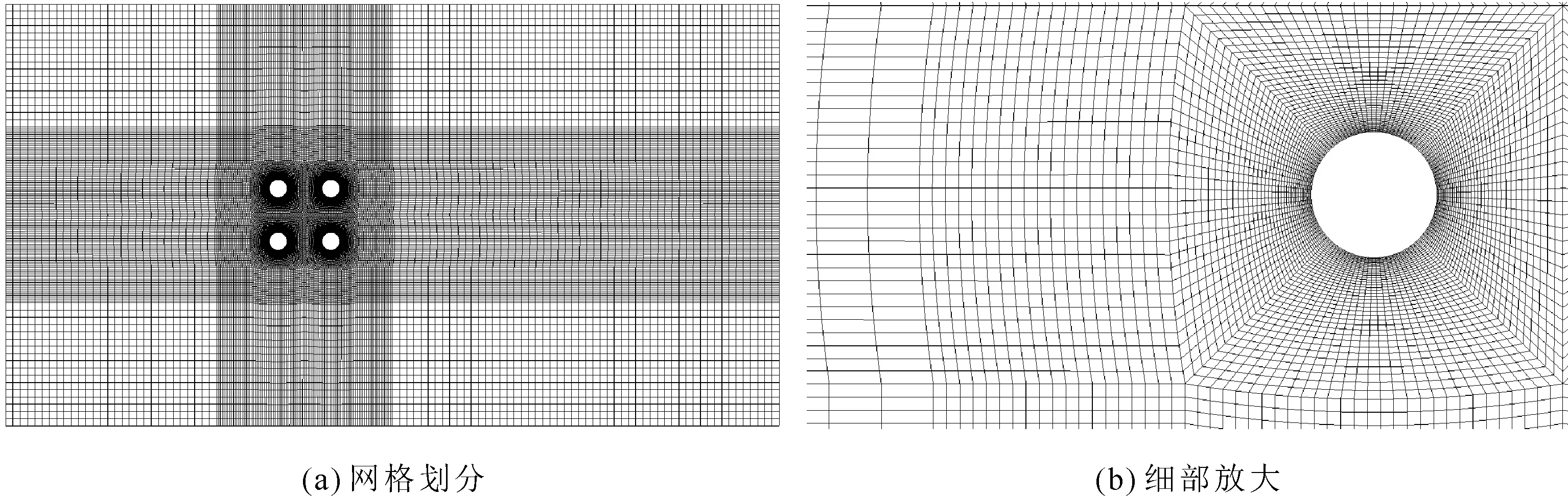
1.5 网格划分
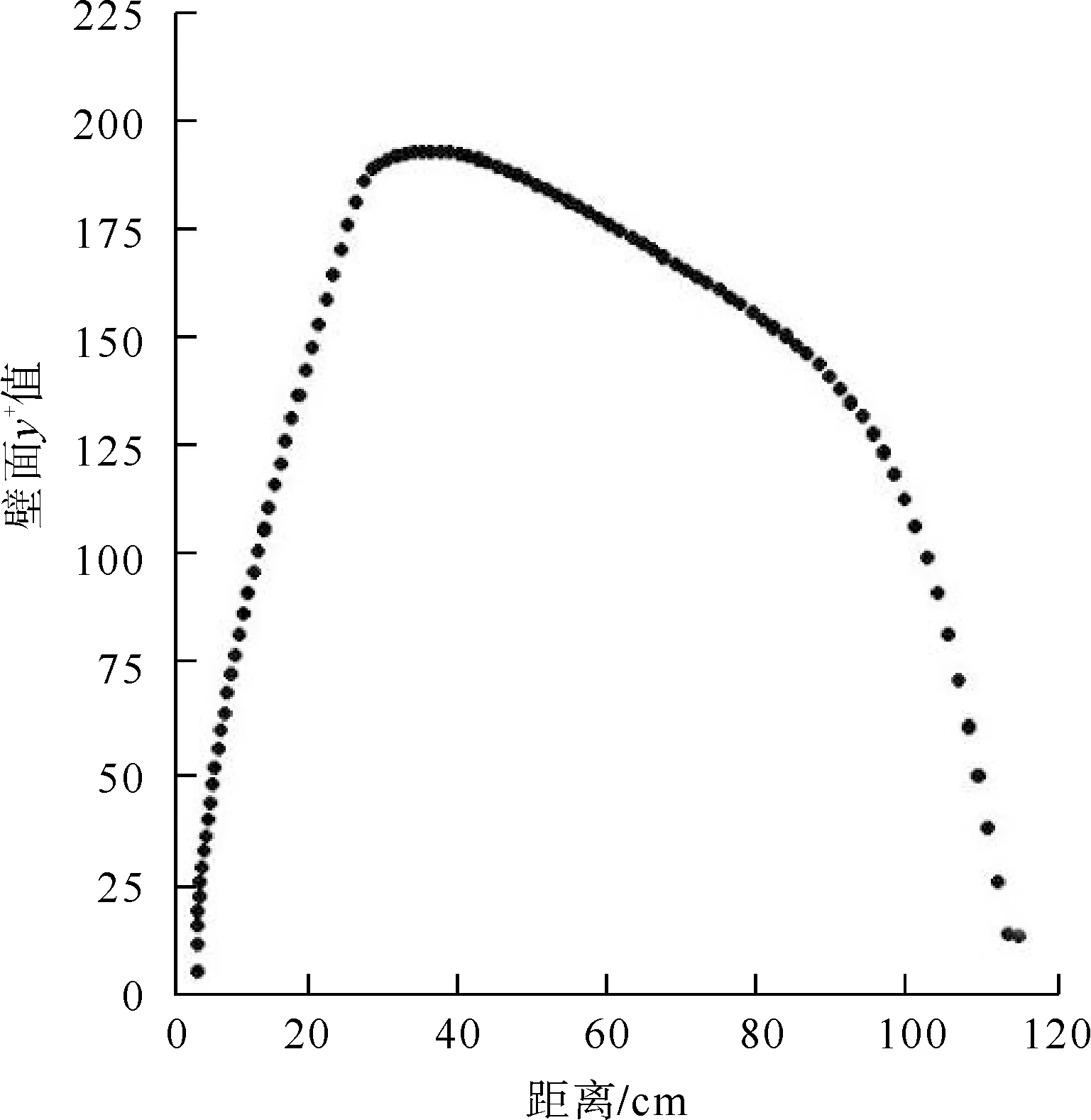
2 模型验证
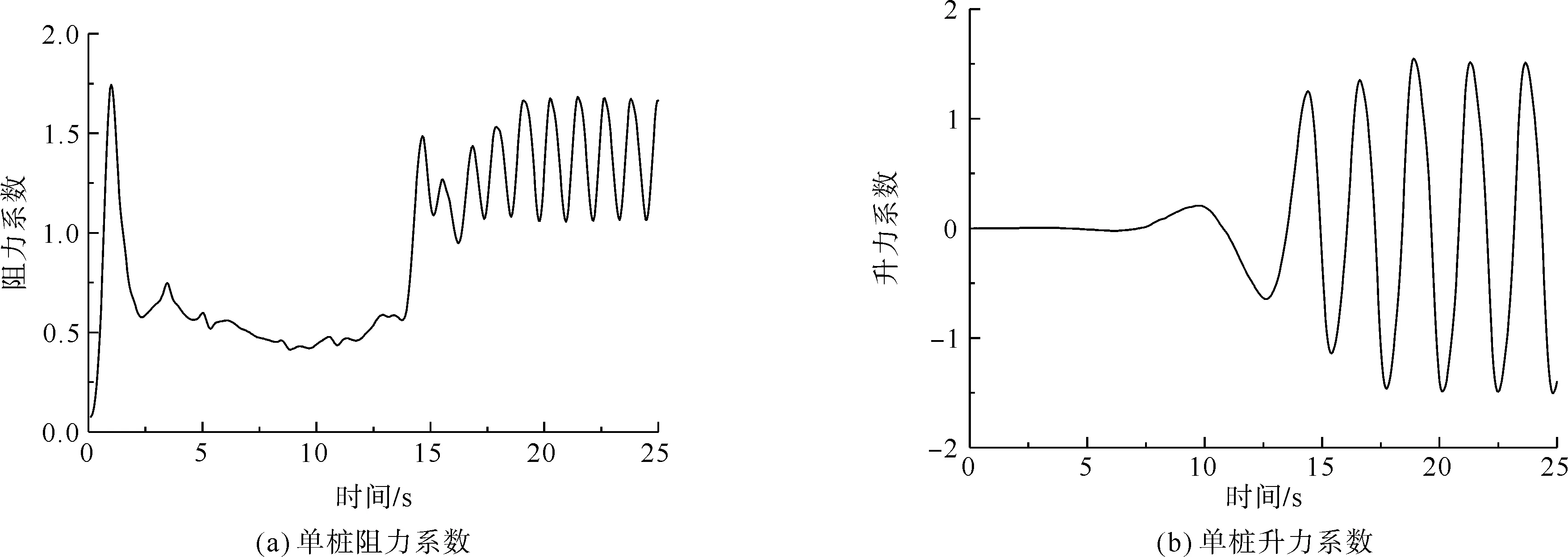
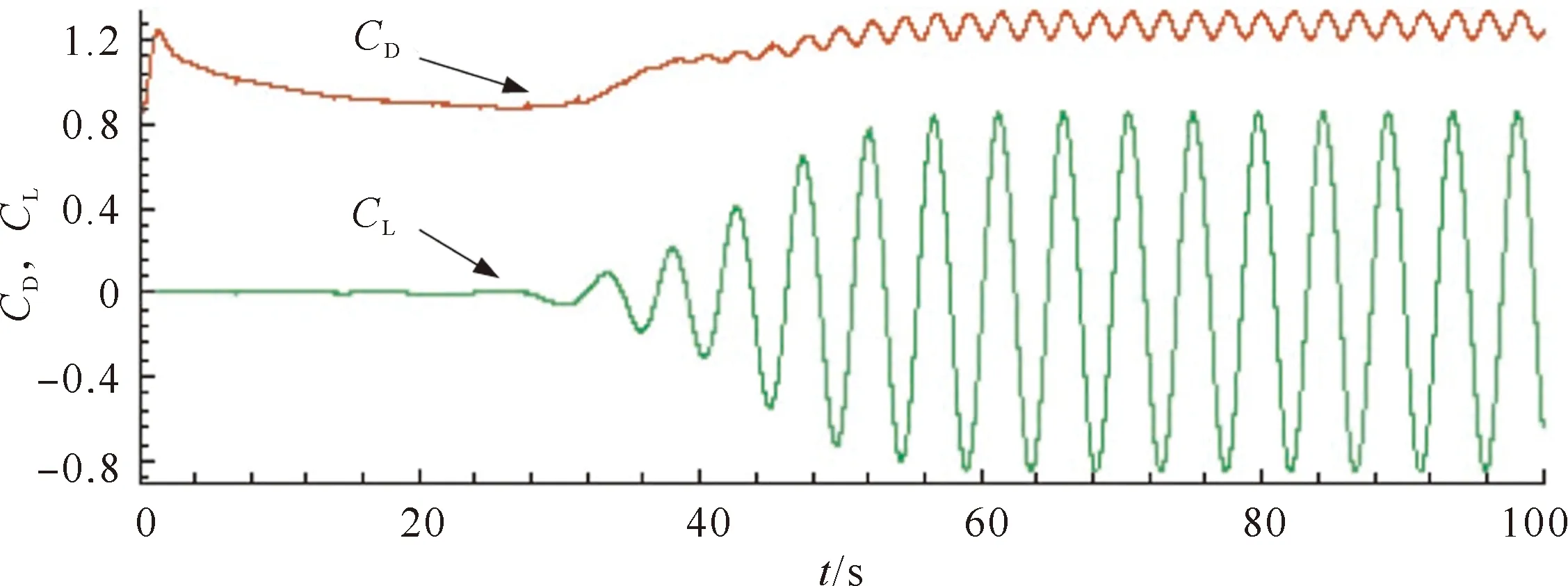
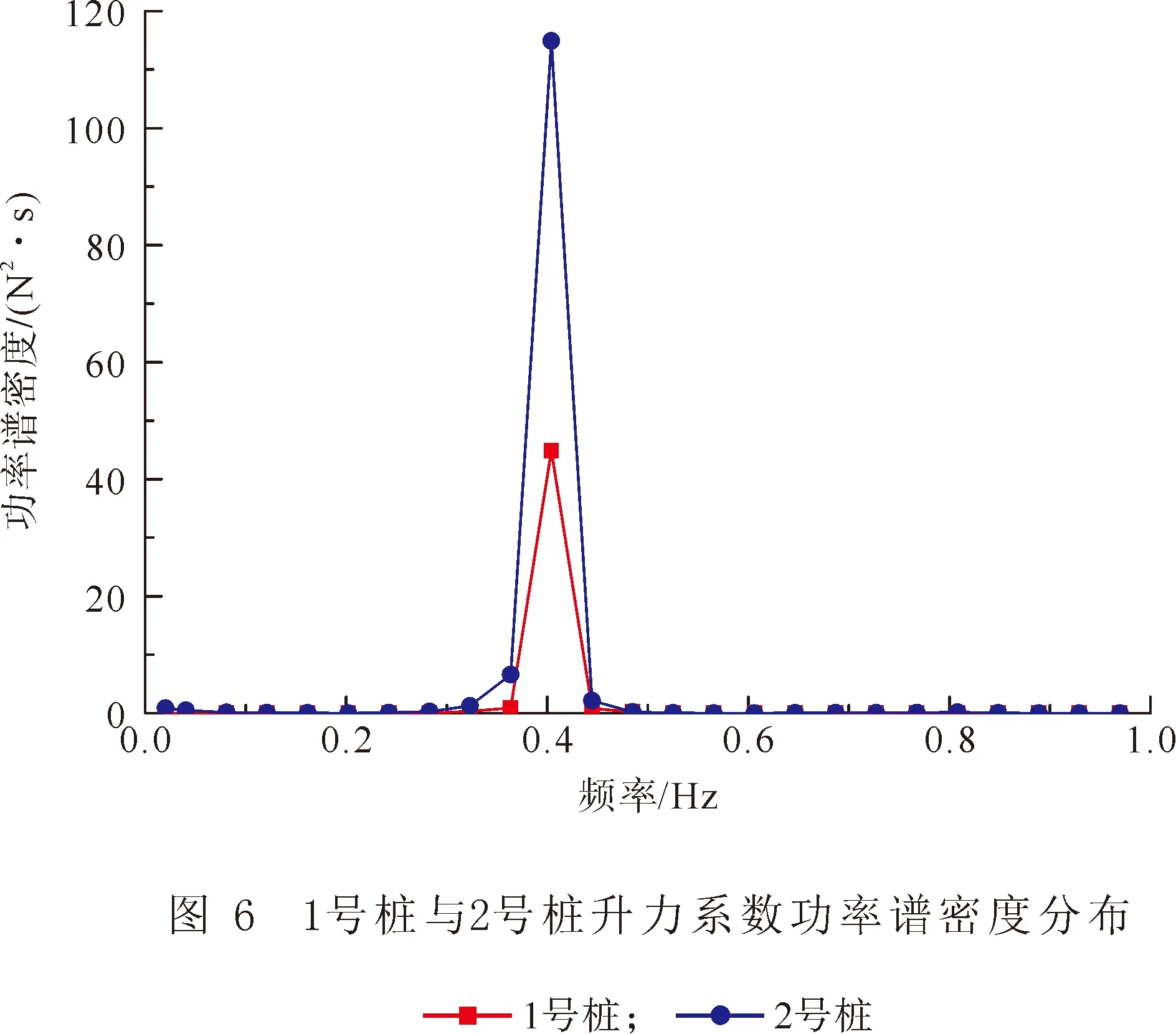
3 计算结果分析
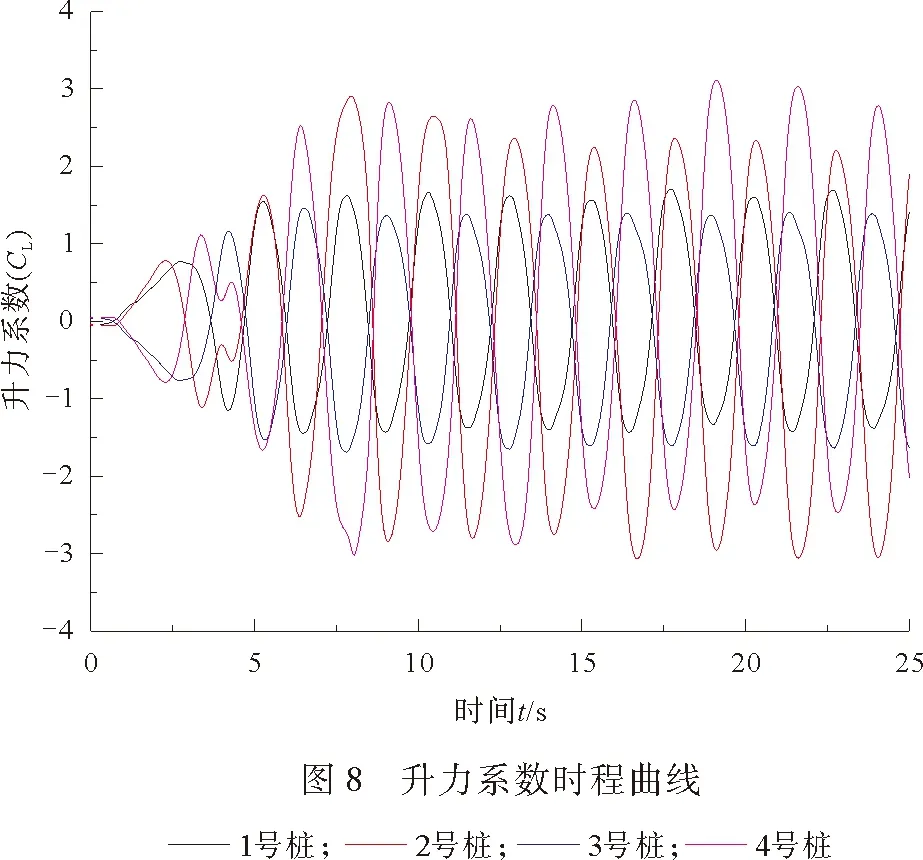
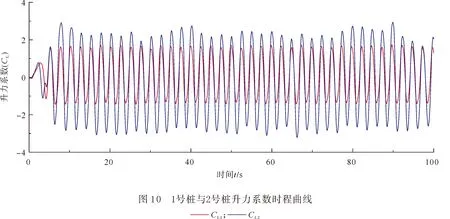
3.1 阻力系数与升力系数分析
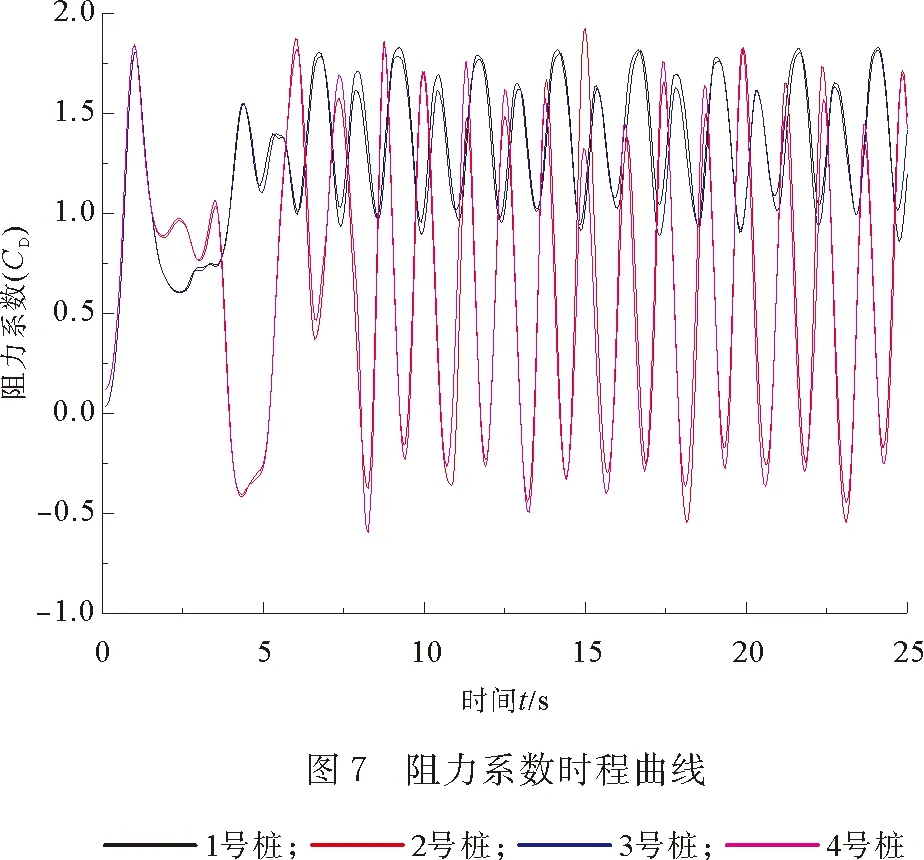

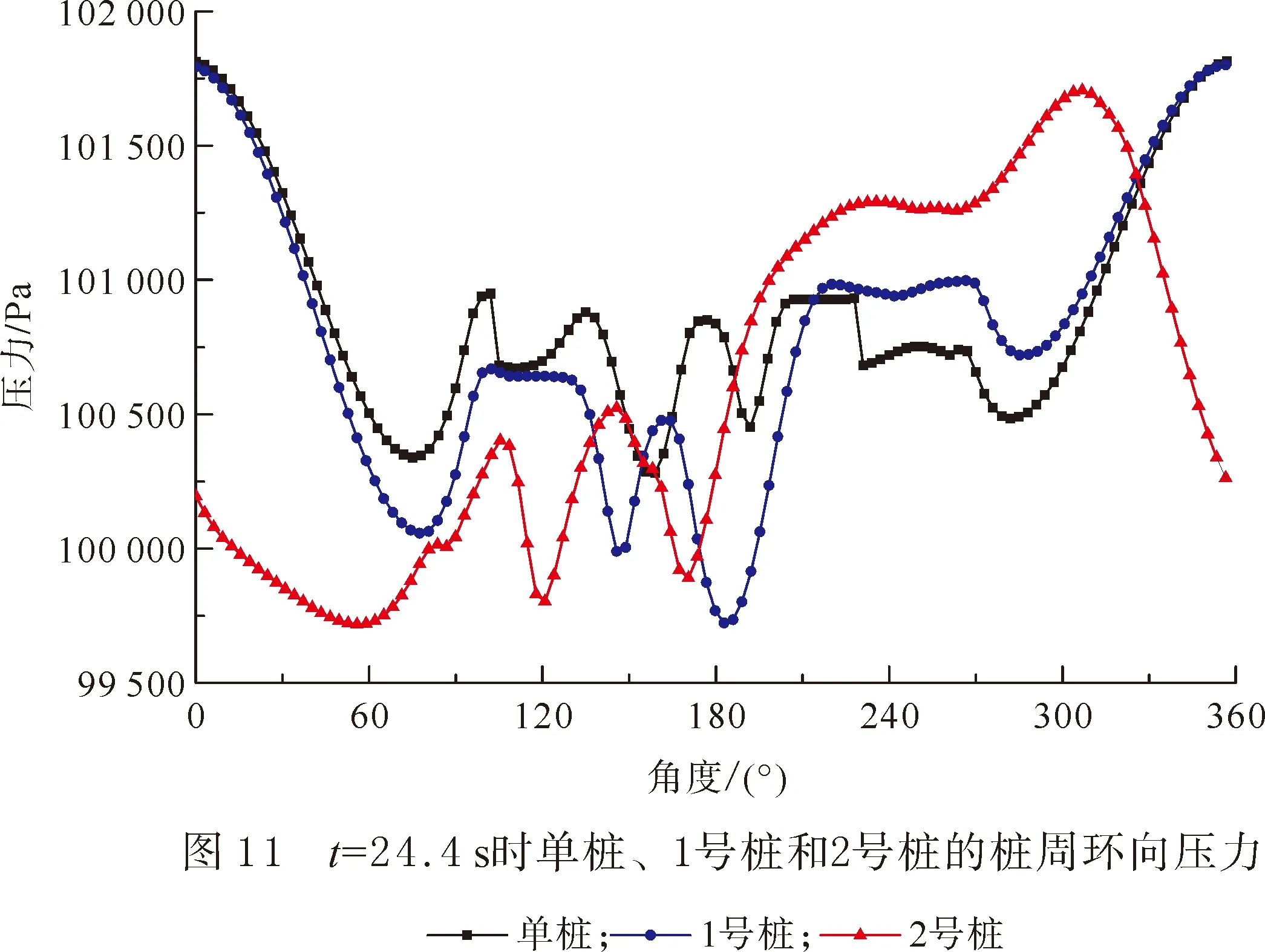
3.2 桩周压力分析
4 结论

