高铁弱胀缩性隧道底鼓病害及仰拱结构分析

宋 锋

(中铁十九局集团轨道交通工程有限公司，北京 101300)

0 引 言

随着中国高铁建设的发展，越来越多的高铁隧道穿越红粘土、古土壤等弱胀缩性地层。在隧道开挖、地下水变动以及施工扰动等因素影响下，势必引起弱胀缩性隧道围岩胀缩作用，胀缩力作用于隧道仰拱，可能会引起仰拱底鼓病害，尤其在运营阶段表现的更为突出。仰拱不但是初期支护施作的最后环节，而且是支护结构形成的关键环节，对支护结构成环、平衡结构内力、控制围岩变形起到至关重要的作用[1]。因此，明确隧道底鼓病害的机理，形成针对该病害的控制措施显得尤为迫切。

学者们对隧道仰拱的影响因素及受力状态展开了许多有益的探索[1-2]。禚振礼通过有限元软件Midas对隧道过渡圆弧、仰拱厚度、仰拱施作时间等影响隧道仰拱受力状态的因素展开了系统研究[3]。王明年等采用模型试验分别对有无仰拱结构的2种方案进行研究，以明确仰拱结构在隧道工程中的作用机理[4]。时亚昕和王明年针对复杂地质条件的长大隧道施工变形问题开展了现场试验研究，指出了仰拱施工中应采用强度增长快受力变形小的干硬性混凝土[5]。吴晓辉针对陇东地区红黏土隧道围岩变形问题展开了系统性研究，发现控制仰拱变形应重视仰拱矢跨比和仰拱厚度的优化[6]。除了对仰拱的影响因素及受力状态研究之外，隧道仰拱施作方案的优化也受到了科研人员的重视。朱合华等通过数值模拟对隧道仰拱结构的施工时间进行了研究[7]；施成华等为研究隧道仰拱结构受力及变形机理，通过现场实测对武广高铁某隧道底部结构的变形和受力进行评估[8]；DU等通过数值模拟手段对软岩隧道在施工中围岩及衬砌结构的受力情况进行反演研究[9]；朱小明等关注公路隧道仰拱病害的致灾机制，分析仰拱失稳塌方的力学机理及处置方法[10]；高峰等借助ANSYS软件对隧道仰拱结构的抗震性能进行优化[11]；魏强等针对高铁隧道服役期内频发的仰拱隆起问题展开了系统性研究，通过工程地质分析、数值计算指出了仰拱变形主要与高地应力、列车动载以及地下水有关[12]。

目前对隧道仰拱的研究主要集中在开挖对围岩稳定性以及仰拱的变形机理方面，而从仰拱开挖支护以及施工方法等层面对仰拱进行优化和创新的研究相对少见，特别对穿越弱胀缩性地层高铁隧道仰拱底鼓形成机制的研究更为少见。因此，有必要对仰拱结构的受力及设计优化展开系统研究，以期为隧道工程仰拱结构的安全施工及健康服役提供保障。

笔者以某具体高铁隧道为依托，采用正交试验手段对5个主要致灾因子进行分析，进而明确减少仰拱底鼓病害的致灾因子及控制方法；通过理论推导，明确了隧道仰拱结构的受力机理及合理拱线形式；进而通过数值计算，对不同矢跨比及混凝土厚度的衬砌进行内力分析，获得合适的结构参数；最后通过改变仰拱结构的矢跨比来对仰拱结构进行优化，得到了穿越红粘土等弱膨胀地层高铁隧道仰拱最优矢跨比。

1 隧道仰拱底鼓致灾因子分析

在大量调研的基础上发现，影响仰拱变形的因素众多，主要包括隧道围岩性质、隧道洞径、仰拱曲率半径、仰拱厚度、衬砌混凝土强度以及施工情况等[13-15]。

1.1 试验方案

基于正交试验的原理，选取隧道围岩性质、隧道洞径、仰拱曲率半径、仰拱厚度、衬砌混凝土强度5个因素进行分析。以陇东地区高速铁路隧道为依托，考虑其围岩具有弱胀缩性，依据《铁路工程土工试验规程》(TB 10102—2010)，测得其最大无荷膨胀率δe=7.12%，最大膨胀力为71 kPa。综合之下选取Ⅲ级、Ⅳ级、Ⅴ级的围岩等级，15.3，13.3，12.3 m的隧道洞径，12.96，15.96，18.96 m的隧道仰拱曲率半径，450，600，750 mm厚度的仰拱厚度以及C20，C25，C30的混凝土强度为试验变量，利用数值模拟软件进行试验，具体试验参数的选取参考《高速铁路设计规范》(TB10621—2014)。

1.2 试验模型

考虑到数值分析结果更加具有参考性以及数值模型的简易性，本模型的隧道埋深与原工程隧道埋深一致，通过Midas数值模拟软件建立为100 m×100 m(长×宽)，厚度为1.6 m的数值分析模型(图1)。模型底部及前后左右采用固定边界条件，上部为自由边界条件，其围岩材料的计算采用Mohr-Coulomb本构模型，衬砌结构采用线弹性本构模型(表1、表2)。

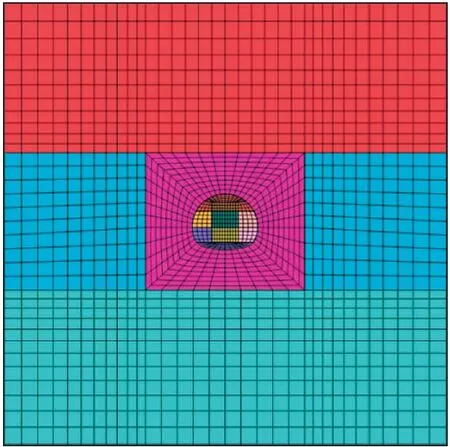
图1 计算模型

表1 隧道仰拱变形各因素水平值

表2 各围岩物理力学参数

1.3 试验结果及分析

从试验结果可知，隧道仰拱变形最大位移通常出现在仰拱中心位。因此，以最大位移作为衡量仰拱结构的标准较为合适，遂将正交试验得到的隧道仰拱中心位置变形进行统计，详见表3。

表3 仰拱位移正交试验计算结果

对数值计算的结果进行直观分析，即将各个因素对应同一水平的计算结果相加，用Ti表示，将各个因素对应同一水平的平均值用Li表示。仰拱中心位置底鼓位移量的计算结果见表4，其中极差R为同一影响因素各水平最大平均值与最小平均值之差。

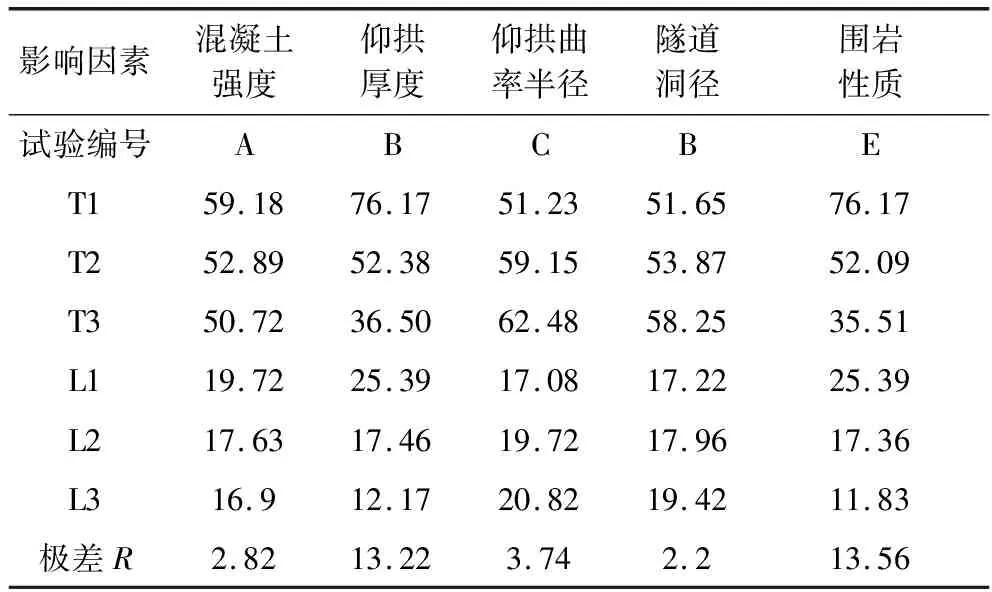
表4 隧道仰拱中心最大变形量的直观分析结果

分析表4可知，隧道围岩性质、隧道洞径、仰拱曲率半径、仰拱厚度、衬砌混凝土强度等5个因素的变化都会对隧道仰拱底部中心位置最大位移量产生不同程度的影响，根据计算结果可知围岩类型对隧道仰拱结构最大变形量的影响程度最大，围岩性质的好坏可直接影响隧道仰拱的变形量，围岩性质越好，变形量也就越小。其次就是隧道衬砌厚度，隧道仰拱曲率半径及混凝土强度，隧道洞径对仰拱结构最大变形量的影响相对较小。其中仰拱底部中心位置最大位移量与隧道的洞径及隧道仰拱曲率半径呈正相关，即减小仰拱曲率半径或者减小隧道洞径可使得隧道仰拱底鼓变形量减小；隧道仰拱底部中心位置最大位移量与衬砌混凝土强度及仰拱厚度呈负相关，即增大衬砌混凝土强度或增大隧道仰拱厚度可以有效抑制仰拱最大变形量。

通过正交试验分析可知，隧道围岩性质、隧道洞径、仰拱曲率半径、仰拱厚度、衬砌混凝土强度等5个影响因子都会对隧道仰拱的变形和受力产生较大影响，隧道围岩条件越好，仰拱结构越可靠；减小隧道仰拱结构曲率半径会使隧道的断面形式逐渐向圆形断面过渡，因此当隧道断面越接近圆形时，隧道结构的受力及变形状态会更优，可以有效地改善衬砌上部结构的受力状态以及使得隧道仰拱结构变形最小；增加仰拱结构的厚度和提高衬砌结构混凝土强度可以有效地抑制隧道仰拱的隆起变形，但对仰拱受力状态的改变有限，因此不能单纯依靠增加仰拱厚度来改善仰拱隆起位移。为了降低工程成本、保证工期及提高工程效率，最大限度对其优化能够有效抑制隧道围岩胀缩性对工程带来的影响，综合考虑工程的实际情况，是否可通过单个影响因素的优化来达到优化的目的，需全面考虑，对于围岩性质，这是很难改变的，也不具备条件改变，但本研究必须考虑围岩性质对结构的影响；同时为满足隧道功能的合理性与适用性，暂且保持原设计洞径；对于仰拱厚度的改变可通过仰拱的回填与开挖来到达到优化目的，一味增加仰拱厚度会增加工程成本，且优化效果不佳；将衬砌结构混凝土强度提高会出现大量的返工造成不必要浪费以及会产生大量的水化热，在这种具有胀缩性的隧道中会造成更多潜在的不利因素。综上所述，建议通过对隧道仰拱曲率半径和仰拱厚度2个方面进行优化，进而满足工程实际情况，保证施工和后期运营安全。

2 弱胀缩性土隧道仰拱结构优化

在明确隧道仰拱受力机理的基础上，推导出了隧道仰拱合理拱线，并采取调整仰拱曲率和混凝土厚度的方式进行结构优化。

2.1 仰拱受力机理及合理拱线分析

2.1.1 围岩基底反力的计算

胀缩力作用下，结构及围岩承受自上而下的作用力以及由于拱效应产生的围岩压力[16]，因此，计算围岩基底反力时需将这2种力叠加，受力模型如图2所示。为了描述仰拱的受力状态，取均布荷载q2处单元体为研究对象(图3)。

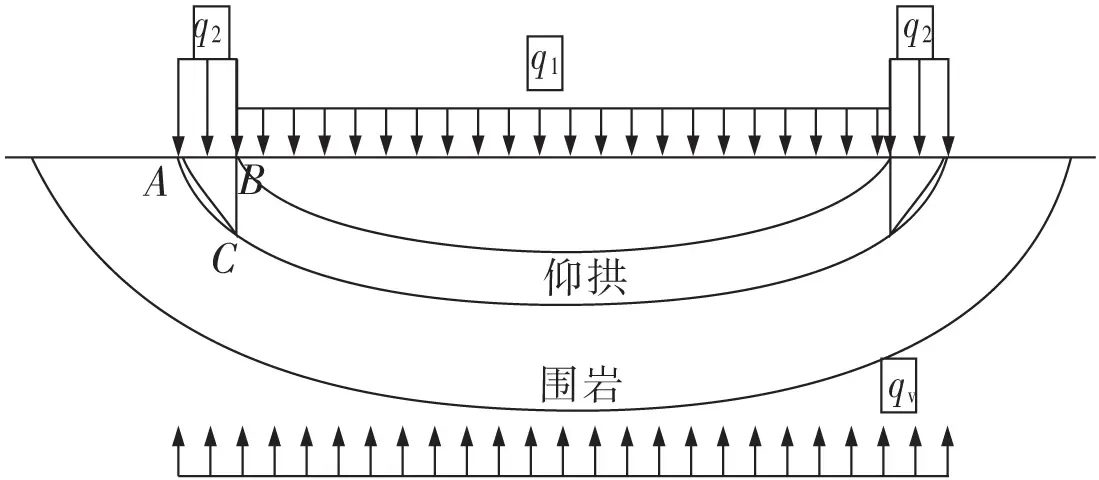
图2 仰拱基底受力模型

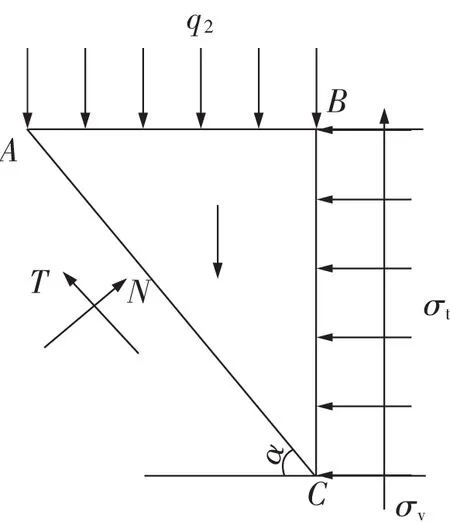
图3 单元体受力示意

分析图3，根据受力平衡求得

(1)

式中N为仰拱所受法向围岩压力；T为切向围岩压力;α为围岩与水平面的夹角；σt为侧向单元应力；σv为侧向单元切应力；b为单元厚度；γ为单元体的密度系数。求得σt,σv，将其施加于力学模型之上，其仰拱-围岩的受力模型(图4)，假定仰拱拱线OBB′为对数螺旋线，可知其方程为

r(θ)=r0exp[(θ-θ0)tanα]

(2)

据相似定理可得

(3)

式中R为仰拱中心点与仰拱下沿的直线距离；R′为仰拱中心点与仰拱上沿的直线距离；α0,θ0,β均为辅助线的相关夹角，如图4所示。对仰拱结构AA′B′B单独进行受力分析，根据结构体受力平衡可得

图4 仰拱-围岩受力模型

qv×2R′sinβ=q1×2R′sinβ+G+σv

(4)

(5)

式中k1和k2为常数，与仰拱尺寸有关。据此，代入参数便可求得地基反力。

3.1.2 膨胀力作用下合理拱线分析

将隧道仰拱所受胀缩力简化为沿隧道结构表面垂直分布的均布荷载，如图5所示。

图5 膨胀力作用下仰拱受力模型

仰拱内力与荷载的微分关系如下

(6)

式中R为仰拱半径;FN为微元所受到法向正向力；FQ为微元所受的侧向切应力；M为微元所受的弯矩；发现在胀缩力作用下，仰拱上任一微段的法向荷载表示为q，而轴向荷载p=0，而若作为合理拱轴又要求M=0，根据曲杆内力与荷载的微分关系可知：q为一常数。

进一步推导可得

(7)

计算可知仰拱轴线的曲率半径为常数，因此在具有胀缩性黏土地层中隧道仰拱的最优拱轴线应为圆弧线。

2.2 隧道仰拱结构矢跨比优化

2.2.1 试验方案

一般而言，黏土地层中的仰拱结构应该为圆弧状，通过改变仰拱结构的矢跨比来对仰拱进行优化[17-18]，对隧道结构的受力、位移的对比分析，得到最优矢跨比(表5)。

表5 仰拱矢跨比优化方案

2.2.2 试验参数

对于隧道仰拱结构矢跨比和厚度优化，主要通过Midas数值模拟软件建立隧道二维荷载-结构模型进行对比分析[19-20]，同时为使计算结果更加符合实际情况，以原隧道结构为基本参照，建立不同矢跨比条件下荷载-结构模型。在数值模拟中，选用的材料物理力学参数见表6。

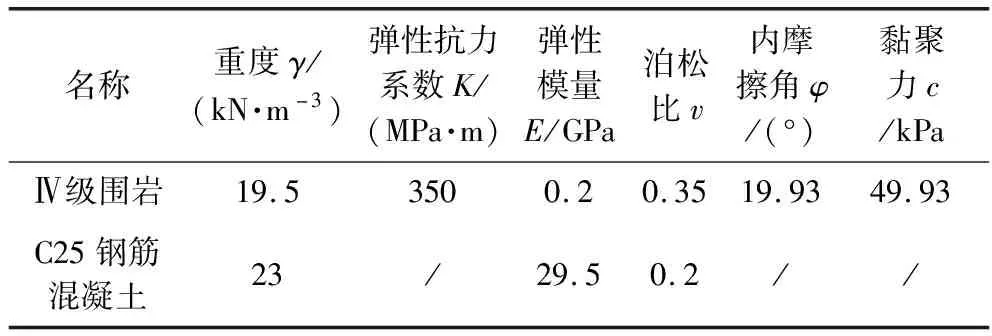
表6 材料物理力学参数

2.2.3 试验结果及分析

隧道衬砌结构的位移变形主要在拱顶与仰拱处，衬砌结构拱顶主要为沉降变形，而仰拱结构主要为底鼓变形。随着仰拱矢跨比的增大，仰拱底鼓变形量逐渐减小，拱顶下沉量先减小后逐渐增大，但增长速率明显减小，而衬砌结构拱脚处的位移量随着矢跨比的增加而逐渐增大，可见矢跨比在0.05～0.07范围内，随着仰拱矢跨比的增大，对隧道拱顶变形具有一定的抑制作用(图6)。

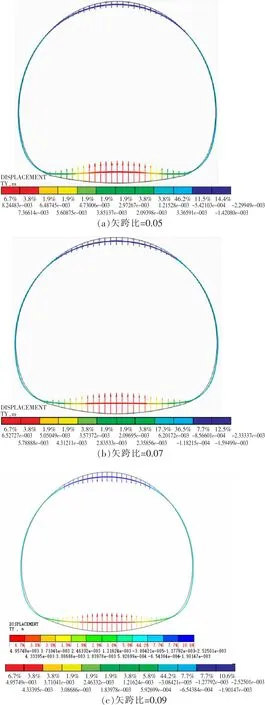
图6 不同矢跨比衬砌结构位移

隧道衬砌结构轴力均匀地沿其结构呈轴线分布，且所受轴力皆为负值，由此可知整个隧道衬砌结构受压，隧道结构拱顶中心位置所受轴力最小，由拱顶到拱脚处逐渐增大，在拱脚处最大，再到仰拱处逐渐减小。因此，在隧道建设过程中，应对隧道拱脚进行加固。随着矢跨比的增大，仰拱所受轴力逐渐减小，拱顶所受轴力先增大后减小。拱脚所受轴力随矢跨比的增大先减小后增大再减小，矢跨比为0.05时所受轴力最大，矢跨比在0.07～0.10范围内，拱脚所受轴力逐渐减小，但减小幅度不大，在1 300 kN附近振荡(图7)。

图7 不同矢跨比结构轴力

隧道衬砌结构的拱顶、仰拱处为正弯矩，内侧受拉；拱肩、拱腰和拱脚处为负弯矩，内侧受压。最大的正弯矩值出现在仰拱部位，且随着矢跨比的增大，弯矩值逐渐减小；最大负弯矩出现在拱脚处，且其绝对值随着矢跨比的增大而减小。过渡圆弧不变的条件下，随着矢跨比的增大，拱脚所受弯矩的状态得到了改善(图8)。

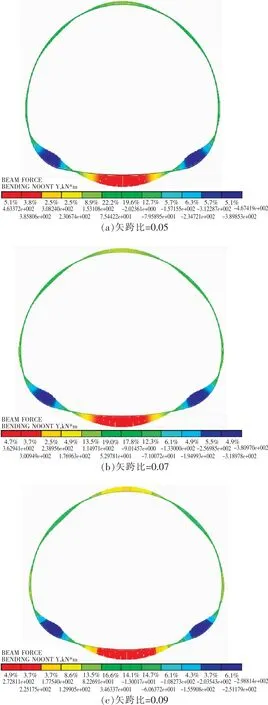
图8 不同矢跨比结构弯矩

2.2.4 安全系数分析

根据《铁路隧道设计规范》(TB 10003—2016)计算隧道衬砌结构各个关键部位的安全系数

(8)

式中K为安全系数；N为轴向力；Ra为混凝土的抗压极限强度；φ为构件的纵向弯曲系数；α为轴向力的偏心影响系数。计算得到隧道结构关键部位安全系数(表7)。

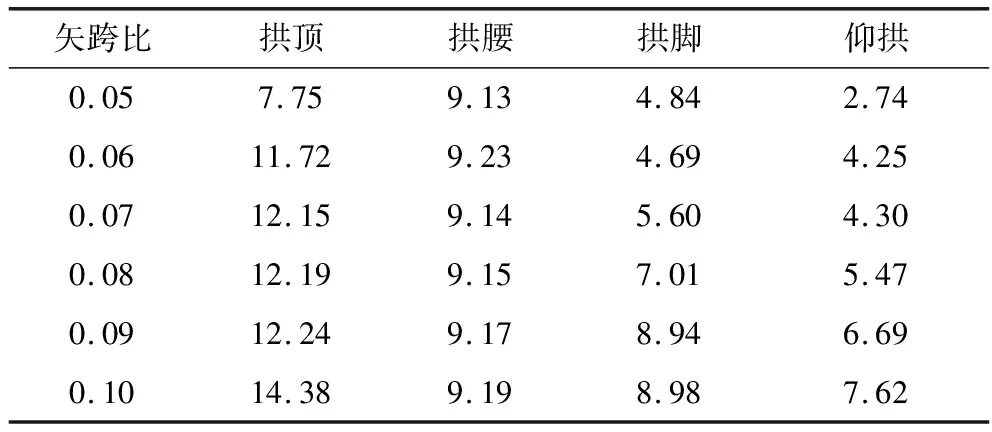
表7 隧道结构关键部位安全系数

2.3 隧道仰拱厚度优化

分析正交试验结果可知，仰拱中心底鼓位移量随着仰拱厚度的增大而减小，同时应考虑仰拱填充及排水等其它附属设施的设计尺寸，该工程隧道仰拱最大厚度为1.07 m(表8)。

表8 仰拱厚度优化方案

图9给出了不同仰拱厚度下拱顶最大沉降量与最大底鼓量(沿重力方向为正向)。当仰拱厚度增大到0.9 m后，其变化趋势减缓；隧道拱顶最大沉降位移量逐渐减小，但变化趋势不明显，说明增大仰拱厚度可以有效抑制仰拱底鼓变形，但对隧道拱顶沉降的抑制作用有限。

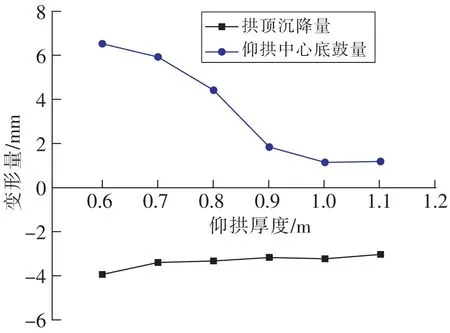
图9 不同仰拱厚度下拱顶最大沉降量与最大底鼓量

3 结 论

1)围岩等级及胀缩性对隧道仰拱结构最大变形量的影响最显著，衬砌厚度次之，仰拱曲率半径、混凝土强度、隧道洞径的影响相对较小。

2)考虑围岩胀缩性对仰拱结构的影响，着眼于隧道仰拱曲率半径和仰拱厚度两方面展开优化，发现增大仰拱厚度可有效抑制仰拱底鼓变形，但对隧道拱顶沉降的抑制作用有限。

3)将仰拱结构单元简化为三铰拱模型，将其所受胀缩力简化为沿隧道结构的均布荷载，分析发现在合理拱轴线的条件下，仰拱结构所受最大轴力与其矢跨比呈反比，且矢跨比越大，仰拱与过渡圆弧接茬处所受轴力越大，对拱脚产生的影响越显著。