基于Rasch模型的体育专业学生Excel考试质量分析

张国瑞 沈阳体育学院

计算机应用基础课是各类高校均开设的一门重要的公共基础课程，其教学内容包括计算机基础知识、Word文字处理、Excel电子表格和PowerPoint演示文稿。结课后采用无纸化考试的方式对学生Word、Excel、PowerPoint等软件的操作能力进行考核，本研究对其中的Excel考试试题质量进行分析，国内进行试题质量分析大多是在经典测试理论（classical testing theory，CCT）的基础上进行分析，这种方法计算简单但存在一些局限性，对抽样质量要求过高、测量出的信度也存在一定的不准确[1]，也无法分析出学生的能力水平。而项目反应理论（item response theory，IRT）可以有效弥补CTT的不足。该理论中的Rasch模型目前应用也比较广泛，这是一种利用数据拟合模型的分析方法，当数据拟合度差的时候可以根据模型需求对数据进行修改以便得到合理的模型，这个过程正好适合对考试试题做分析，不理想的试题可以根据模型理论进行修改[2]。因此本研究将Rasch模型引入到Excel考试的质量分析中，通过科学的定量分析，验证试题的难易度以及学生的能力水平，为了日后修订试题库，提高试题质量提供理论依据。

一、研究对象与方法

（一）研究对象

本研究为了分析体育类专业学生Excel试题质量，随机抽取体育教育、运动训练、社会体育指导员等专业289名学生的Excel考试成绩，学生考试过程采用计算机无纸化考试系统，全部试卷由系统自动判分，极大地避免了人为判卷中可能出现的误差。本次考试Excel共有22道题，每题答对计1分，答错计0分。

（二）研究方法

使用WINSTEPS 5.1.5.2软件对所得数据进行Rasch分析，主要研究分析的内容为：总体拟合情况、单维度检验、题目与个体分析、怀特图、气泡图等，通过上述分析研究试题质量并提出修改建议。

二、研究结果

（一）整体质量检测

将考试数据导入Winsteps 5.1.5.2进行分析，试题的整体质量一般用拟合指数MNSQ（包括IMNSQ和OMNSQ）来表示。本次考试中学生和题目的拟合值数MNSQ（包括IMNSQ和OMNSQ）均接近理想值1，表明考试成绩与Rasch模型的拟合度比较高。学生的分离度（PSI）为2.33，高于临界值2，信度（PR）为0.84，高于临界值0.8，综合这两个指标说明参与本次考试的学生样本能力分布比较合理。试题的分离度（ISI）为5.69，高于临界值2，信度（IR）为0.97，高于临界值0.8，综合这两个指标说明试题的区分度比较理想。

（二）单维性检验

单维性是Rasch模型使用的前提条件之一，试题满足单维性是指该试题考查学生某种单一能力或潜在特质。本研究利用Winsteps 5.1.5.2对残差进行主成分分析（PCA），这样可以将相关项目转换为主成分，由此计算出来的解释方差可以衡量模型的单维性，这里通常要求通过测量解释的原始方差应大于50%，第一次对比未解释的方差应小于3.0，本次考试成绩残差主成分分析结果，通过测量解释的原始方差为58%，第一次对比未解释的方差为2.76。说明本次考试数据满足单维性的要求，适合做Rasch模型分析。

（三）各试题拟合度分析及误差统计

应用Rasch模型分析实际数据时，还需要对该数据进行模型拟合度检验。该检验可以分析数据与模型的拟合情况，只有拟合情况符合要求时对实际数据进行Rasch分析才具有实际意义。Rasch拟合度分析中常用的指标是INFIT MNSQ和OUTFIT MNSQ，INFIT MNSQ是加权后的残差均方，用来分析试题难度与所对应的学生能力水平是否相符。OUTFIT MNSQ是标准残差的均方，用来分析异常数据。通常情况下这两个MNSQ值介于0.5到1.5之间时，数据与模型的拟合程度可以接受，当该值为1时，数据与模型完全拟合。此外该值大于1.5时表示学生在答题时，作答方式与模型设定的方式不一致，即数据与模型不拟合[2]。该值小于0.5时，表示学生对某题的答题结果差异很小或者说这道题无法区分学生之间能力水平上的差异，即数据与模型过度拟合[1]。在对数据进行拟合度检验时可能出现INFIT MNSQ和OUTFIT MNSQ的结果不一致的情况，此时我们一般以INFIT MNSQ为准[1]。

本次考试各试题拟合度及误差统计中题目Q1的INFIT MNSQ和OUTFIT MNSQ均大于1.5，说明该题目在测量学生与之相对应的能力时存在一些干扰因素。题目Q2的INFIT MNSQ和OUTFIT MNSQ均过小而无法测量，该题目回答的正确率为100%，无论能力水平高低，全部学生均答对了这道题，该题目区分度极差。其余题目INFIT MNSQ都在合理范围内，数据拟合度良好。

（四）试题难度与学生能力水平分析

为了直观的展示题目难度与学生能力、各题目难度、各学生能力之间的关系，本研究采用Rasch模型中的怀特图，见图1。怀特图可以将Rasch模型中根据原始数据转换成等距的logit值，将试题难度和学生能力放到同一量尺中进行标定，从而直接比较题目难度与学生能力、各题目难度、各学生能力之间的差异。

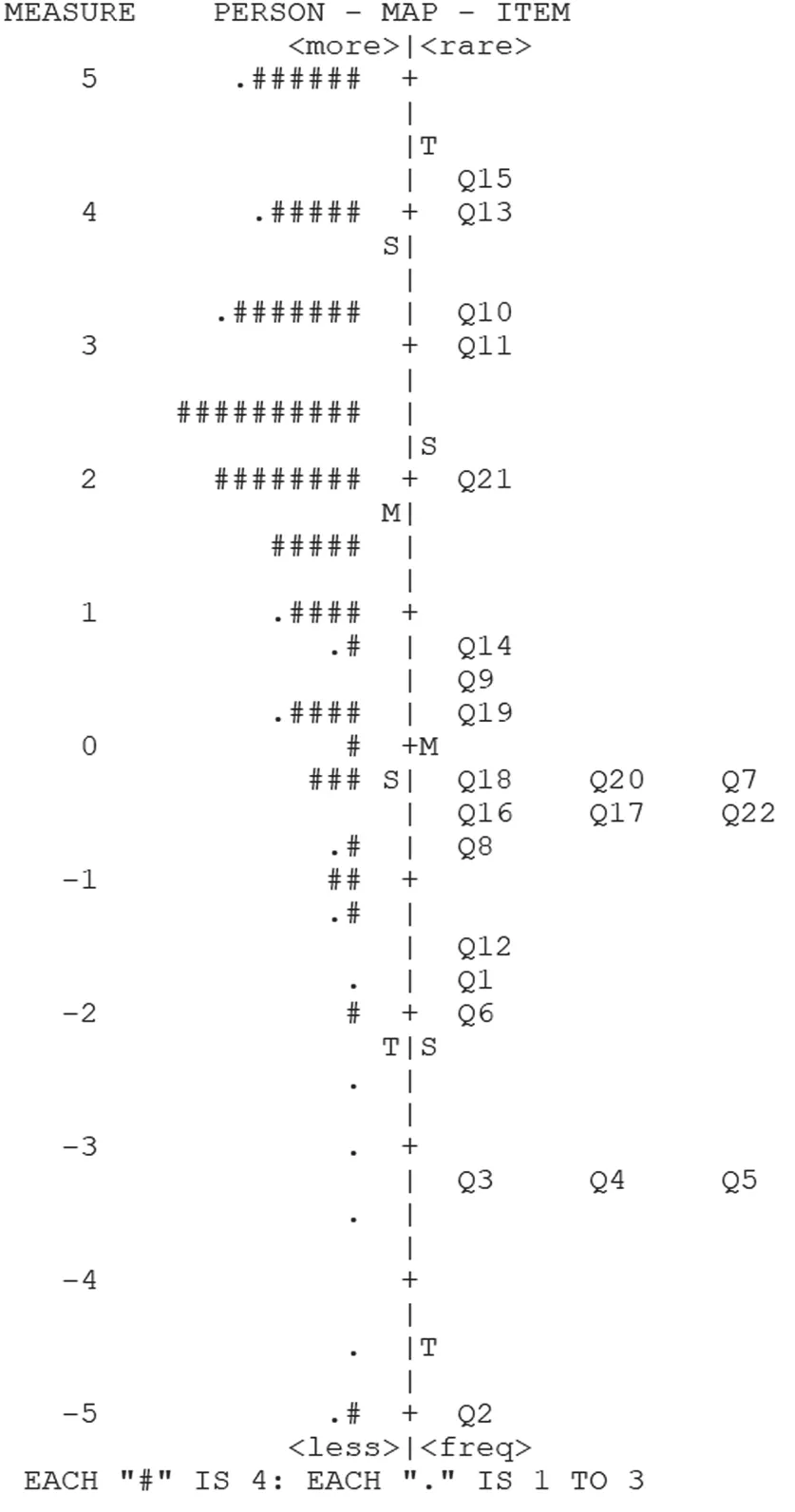
图1 学生能力与试题难度关系怀特图

图1中，中线是logit刻度尺，中线左侧表示学生的能力，中线右侧表示试题的难度。图中M表示平均水平，S是距离平均值一个标准差的距离，T是距离平均值两个标准差的距离。刻度尺由上往下表示学生能力和试题难度的逐渐降低。中线左侧的每一个“#”代表4名学生，每一个“.”代表1至3名学生。从图1中可以看出本次考试学生能力的均值比试题难度均值高出将近2个logit的值，说明本次考试试题整体难度过低。其中，题目Q2、Q3、Q4、Q5难度都低于学生平均能力两个标准差以上，对大部分学生而言这四道题没有什么区分度。同时有25名以上的学生能力水平比难度最大的题目Q15的难度高了将近1个logit，说明对这一部分学生没有能够与之相匹配的题目。同样在学生能力均值附近仅有1个题目Q21，在这一水平附近的学生人数最多，需要比较多的同等难度的题目来对学生进行测试，本次考试中仅有1道题显然不够。

三、结论与建议

本研究使用Rasch模型分析体育专业学生Excel考试的试题质量，通过分析可以认为Rasch可以很好地对本次考试进行分析。本次考试试题整体质量比较高，与Rasch模型拟合度比较高，整体区分度也比较理想，但是整体的难度比较低。本次考试Excel试题是从2018年建立的试题库中随机抽取的，试题难度是按当时学生的一般水平编写的。2018年以来对体育类学生《计算机应用基础》课进行了不断地教学改革，从以教师为中心逐步转变为以学生为中心，从单一的线下授课转变为线上线下混合式的教学，在提升学生自主学习能力的同时也在不断地提升学生对于Excel操作的水平。从本次考试的Rasch模型分析结果中可以看到，学生的能力水平已经高出试题难度将近2个logit，这个差距已经非常明显的说明了学生能力有了显著的提升。由此可见本课程Excel试题库应该根据学生现有能力水平进行大范围修订。

此外，由于本次考试整体难度比较低，其余题目虽然在Rasch模型分析中未发现问题，为了提高试题整体难度，在试题修订中也应在原题要求基础上适当增加题目难度。与此同时，建议调整教学大纲，增加一些学习难度比较大的Excel操作知识。