高架轨道典型结构内损耗因子实验及验证

余亮亮，雷晓燕，罗锟，王鹏生

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

近年来，城市轨道交通在我国得到了迅猛发展，然而在城市轨道交通体系中，高架轨道占比只有百分之十几。其中，制约着高架轨道结构在城市交通体系运输中发展的主要原因是高架轨道结构的辐射噪声。

统计能量分析方法适合对系统高频特性进行研究，而有限元法通常用于中低频的结构振动响应分析。为了扩大统计能量法的分析范围，混合有限元统计能量分析方法成为众多国内外学者的研究的重点，并且已经在航空航天、船舶、汽车等领域的噪声分析中得到了广泛应用[1-3]。

采用混合有限元统计能量法进行高架轨道结构噪声分析的重难点是获取高架轨道结构子系统的模态密度、内损耗因子以及耦合损耗因子等关键参数[4]，其中，损耗因子是衡量系统阻尼特性并决定系统耗散能力的重要参数，对高架轨道结构噪声预测具有重要意义，一般可以通过理论分析和实验测试等方法获得[5-7]。实验测试法是损耗因子测试最准确的方法，主要包括瞬态衰减法、稳态能量流法等。稳态能量流法测试的关键是需要准确计算输入功率，因此在给测量损耗因子带来不便的同时，产生的误差也比较大。瞬态衰减法可以快速估算结构的损耗因子，且无需测量输入功率，统计误差相对不大[8-9]。

本文基于瞬态衰减法的基本原理，对高架轨道典型混凝土薄板的内损耗因子进行实验测试，并对其规律进行分析，基于损耗因子测试结果，建立混合FE-SAE模型进行声学计算，并对声学计算结果进行实验验证，在此基础上进行损耗因子参数分析。

1 瞬态衰减法原理

假设结构荷载冲击之后的加速度响应信号为实函数，对应的Hilbert变换为[5]

其逆变换为

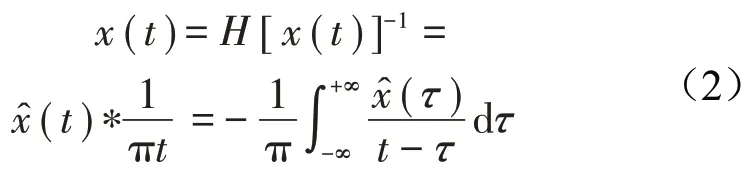
于是得到函数的解析信号为

式中：复数表达式为

式中：A(t)=即为响应信号x(t)的包络，瞬时相位θ(t)=arctan。将响应信号的包络线取对数，即可得到衰减曲线，次曲线的斜率的绝对值即为结构阻尼η，将其除以频率即可得到阻尼比ξ=η/ω,将阻尼比除以2即为测试结构的损耗因子[5]。

2 典型结构损耗因子实验获取

2.1 实验概况

本实验的测试对象为高架轨道典型的薄板结构，尺寸为800 mm×800 mm×30 mm的混凝土薄板结构。实验时采用弹性尼龙绳进行吊装，采用硬度较大的尼龙力锤锤头对试块进行锤击，并采用加速度传感器进行振动响应信号测试。为提高测试的准确性和可靠性，在混凝土薄板上布置5个加速度传感器，传感器的布点位置要避免对称分布和空间均匀分布，此外对物体采取多点锤击实验。实物模型及测点布置如图1（a）、图1（b）所示。图2为实验测试系统简图。

图1 混凝土薄板

图2 瞬态衰减法测试系统简图

2.2 数据处理及实验结果

根据瞬态衰减法原理，对实验测试的加速度信号进行处理。如图3所示。首先将加速度传感器测试得到的加速度时域信号利用MATLAB进行1/3倍频程中心频率滤波处理，得到各频段的加速度时域信号，将加速时域信号进行Hilbert变换的得到解析信号，进而得到响应信号的包络，将包络信号取对数，可得到加速度衰减信号，进一步可得到加速度衰减信号的衰减斜率，将斜率的绝对值除以两倍的中心频率即为结构的内损耗因子[11]。

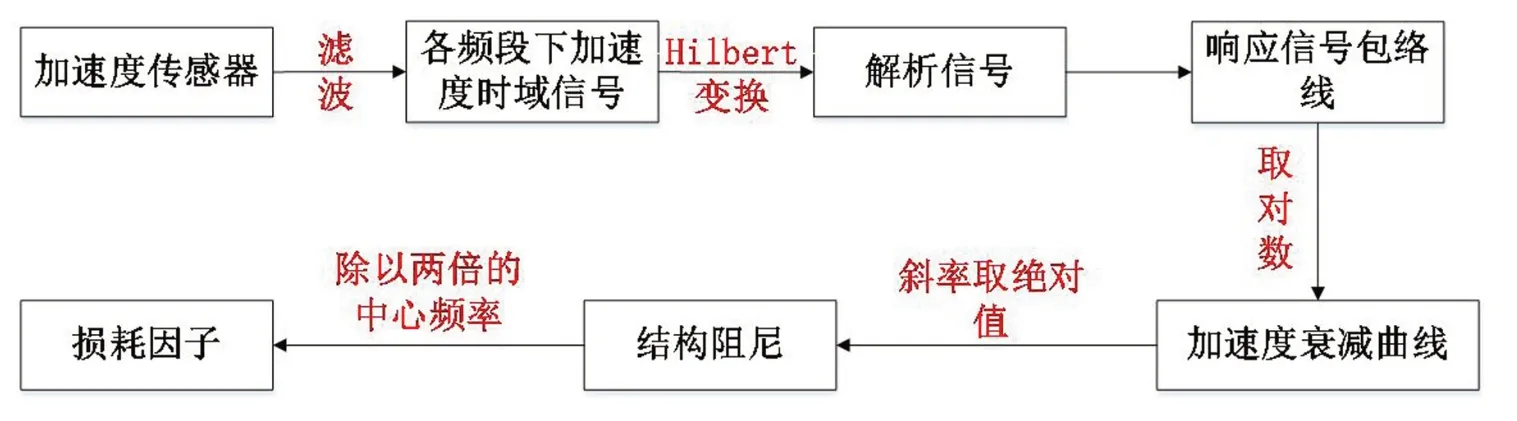
图3 实验数据分析流程

图4为薄板1、3测试通道的时域加速度曲线，显然薄板在冲击荷载作用下加速度呈现衰减趋势。

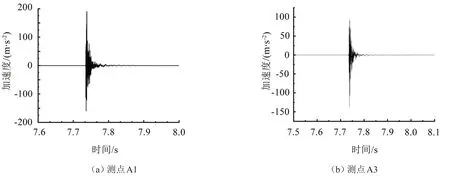
图4 薄板时域加速度曲线

图5为中心频率为500 Hz的A1测点的衰减包络，由图可知加速度响应在前面部分呈迅速衰减状态，其衰减斜率即为所需数据，后半部分为噪声信号量级。图6是A3测点中心频率为160 Hz处的衰减包络线，不同于A1测点，A3测点的衰减由两部分组成，其中第一部分衰减迅速，表现为高阻尼衰减，第二部分衰减稍慢，表现为低阻尼衰减，此时带宽内的损耗因子应该取两部分衰减曲线分别计算得到损耗因子的平均值[7]。

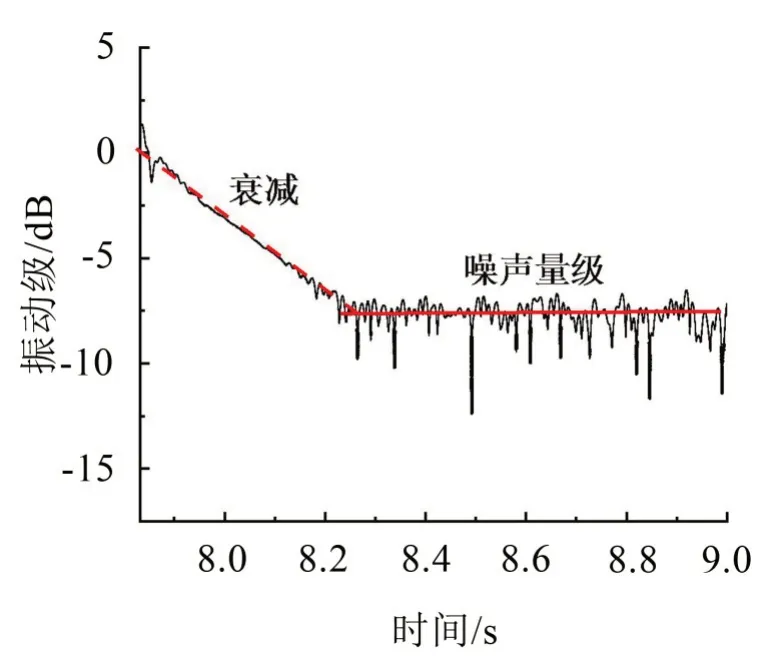
图5 中心频率为500 Hz的A1点的衰减包络

图6 中心频率为160 Hz的A3点的衰减包络

对多点锤击激励测试所得的加速信号进行分别处理，将测试结果取平均，求得结构的内损耗因子，结果如图7所示。由图可知：薄板结构损耗因子主要在0.01～0.02范围内，在各频段内，损耗因子大小在0.016范围上下浮动。

图7 损耗因子测试结果

3 实验结果验证及参数分析

为验证测试结果的准确性，首先建立FE-SEA混合箱梁1/10模型，同时，将结构损耗因子测试的结果导入到混合模型中进行数值仿真计算，再将数值计算结果与实验室结果进行比较，最后进行内损耗因子参数分析。

3.1 混合模型的建立

箱梁模型的主要参数有：弹性模量为30 GPa，密度为2 203 kg/m3，泊松比为0.2。桥上无砟轨道由3部分组成：轨道板、自密实混凝土模拟层和底座板，其尺寸分别为645 mm×255 mm×30 mm、3 200 mm×260 mm×10 mm、3 200 mm×295 mm×19 mm。

根据箱梁的结构特性，可以近似将箱梁结构看成是由顶板子系统、底板子系统、左右翼板子系统、左右腹板子系统组合而成。箱梁的上部具有无砟轨道结构子系统以及钢轨子系统。

将实验测试时激振器的时域荷载导出，采用MATLAB做快速傅里叶变换之后得到频域荷载，然后导入到VAone的混合模型，进行声压级计算。混合模型如图8所示。

图8 箱梁结构混合FE-SEA计算模型

3.2 箱梁声学测试

如图9所示，在箱梁结构跨中断面的N1、N2、N3位置布置3个GRAS声学传感器，对实验室箱梁模型进行噪声测试，实验中采用的主要仪器设备有：HEAD噪声采集分析系统、激振器以及声学传感器等。测试前，做一定的隔声处理，尽可能避免对测试结果的影响。测试分5组进行，每组测试时间30 s。图10为实验室测试现场。

图9 箱梁模型跨中截面测点布置示意图/m

图10 实验室测试照片

3.3 结果分析

图11给出N1、N2、N3测点的声压级实测与仿真的比较，由图可知，各测点的仿真计算结果与实测结果大体趋势一致，说明基于Hilbert变换的瞬态衰减法对混凝土薄板结构的内损耗因子的测试方法是可行的，在20 Hz～50 Hz的低频部分误差较大，可能主要是由于在半消声室内，受地面反射影响。

图11 测点N1、N2、N3的理论值与实测值

3.4 内损耗因子参数分析

为探讨不同内损耗因子对噪声的影响，针对上述模型及测试结果，以N3点为例，选取不同损耗因子进行参数分析。图12为不同损耗因子下场点N3的声压级，由图可知，在不同损耗因子取值下的声压级大小大体趋势是一致的，并且，场点的声压级随着损耗因子的增大而减小，损耗因子取值为0.001时的声压级比损耗因子为0.04时的声压级高出3 dB左右，说明损耗因子对噪声的影响不容忽略。

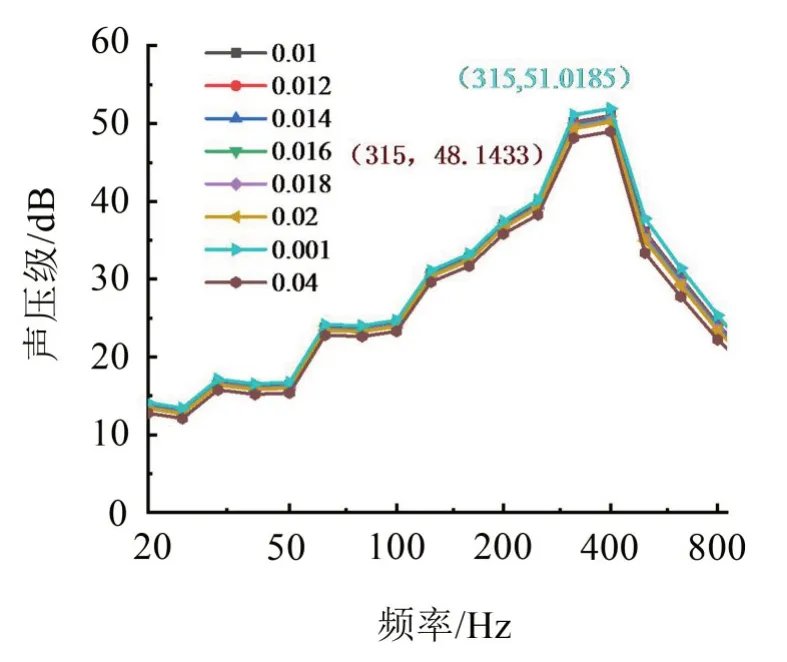
图12 不同损耗因子下N3的声压级

4 结语

本文基于瞬态衰减法，测试薄板结构内损耗因子，分析了混凝土薄板的内损耗因子特性，将测试的结果应用于高架轨道1/10箱梁结构混合FE-SEA模型，并进行内损耗因子参数分析，主要结论如下：

（1）基于Hilbert变换的瞬态衰减法实验进行损耗因子测试，结果表明测试方法的可行性，为高架轨道结构损耗因子研究提供参考。

（2）薄板结构损耗因子主要在0.01～0.02范围内，在各频段内呈现出上下浮动的规律。

（3）高架轨道箱梁结构辐射声压级大小随着内损耗因子增大，呈现出衰减的规律，但总体趋势保持一致。