城市轨道交通橡胶浮置板减振轨道声振特性研究

杨力，张小安，石广田，张晓芸

（兰州交通大学 机电工程学院，兰州 730070）

近年来，我国城市化建设突飞猛进，原有交通体系已经无法满足人们对高效出行的要求。至2018年底，我国已开通城轨交通运营的城市有35个，运行线路总长度达5 761.4 km[1]。城市轨道交通以其节约能源使用、节省地上面积、全天候运量大、安全舒适可靠等特点成为解决城市交通拥堵的主要措施并得到快速发展。

城市轨道交通在人口密集区域穿行，其运行过程中引起的振动和噪声问题已成为限制其发展的关键因素。因此我国城市轨道交通中采用了大量的减振轨道以缓解振动的影响，这些减振措施主要包含了钢轨减振、扣件减振、轨枕减振以及道床减振等。如杨建近等[2]采用数值分析的方法研究了钢轨吸振器对轨道和桥梁结构垂向振动的影响，王志强等[3]采用现场测试的方法研究了GJ-III型减振扣件的减振性能，詹彩娟[4]采用落锤实验的方法对新型减振扣件系统进行了减振性能测试，李大成[5]研究了弹性长枕轨道的减振性能，刘力等[6]现场测试了梯形轨枕的减振性能，Zhai等[7]基于车轨耦合动力学理论探讨了钢弹簧浮置板减振轨道的适用性，孙成龙等[8]对北京5号线钢弹簧浮置板减振轨道进行了测试，黄众[9]对橡胶浮置板减振轨道减振性能进行了现场测试。

减振结构在缓解周围振动的同时，振动能量将会累计于减振轨道，导致其自身的振动被加剧[10]，因此有必要系统研究减振轨道的声振问题。现有研究主要集中于橡胶浮置板减振轨道减振方面研究，如金浩等[11]使用实验法研究了铺设方法对橡胶浮置板减振轨道垂向加速度的影响，郭镇等[12]通过有限元方法研究了减振垫面刚度和浮置板密度对橡胶减振垫轨道减振特性的影响。还有些研究则侧重于研究浮置板减振轨道与桥梁声辐射特性之间的影响，如李小珍等[13]使用有限元-边界元方法研究了钢弹簧浮置板轨道对箱梁振动声辐射总声级的影响，Lin等[14]采用FEM-SEA方法分析了橡胶浮置板对钢桁架斜拉桥结构噪声特性的影响，张晓芸等[15]研究了桥梁顶板对钢弹簧浮置板减振轨道声辐射特性的影响，而对于橡胶浮置板减振轨道自身声振特性的研究较少。

本文以城市轨道交通中常见的橡胶浮置板减振轨道为研究对象，采用有限元-边界元方法建立了移动载荷下车辆-橡胶浮置板减振轨道动力学模型和声学预测模型，对橡胶浮置板声辐射效率、线性声压级、声场分布等声辐射特性进行分析，研究其声振特性。

1 橡胶浮置板减振轨道的动力学分析

1.1 橡胶浮置板减振轨道动力学模型的建立

本文采用车辆-轨道相互作用理论建立了车辆-橡胶浮置板减振轨道耦合动力学模型。如图1所示，模型由车辆子系统和轨道子系统组成。车辆子系统是由1个车体、2个构架和4个轮对构成的35个自由度车辆系统，详细建模参数参见文献[16-17]。

轨道子系统由钢轨、扣件系统、浮置板、橡胶垫层和底座构成。使用有限元方法建立橡胶浮置板动力学计算模型，如图2所示，建模参数如表1所示。

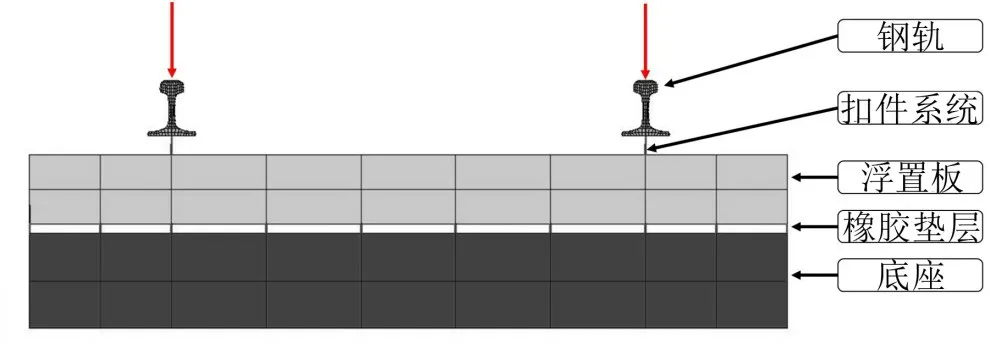
图2 橡胶浮置板减振轨道有限元模型

1.2 橡胶浮置板减振轨道动力学分析

基于上述分析模型模拟地铁A型车在80 km/h的速度下通过铺设橡胶浮置板减振轨道线路时的动力学响应，研究橡胶浮置板自身振动引起的低频声振特性。由于测试的地铁线路为新建线路，线路平顺性较好，因此在仿真模拟时采用较为平顺的美国六级轨道谱作为激励[18]。

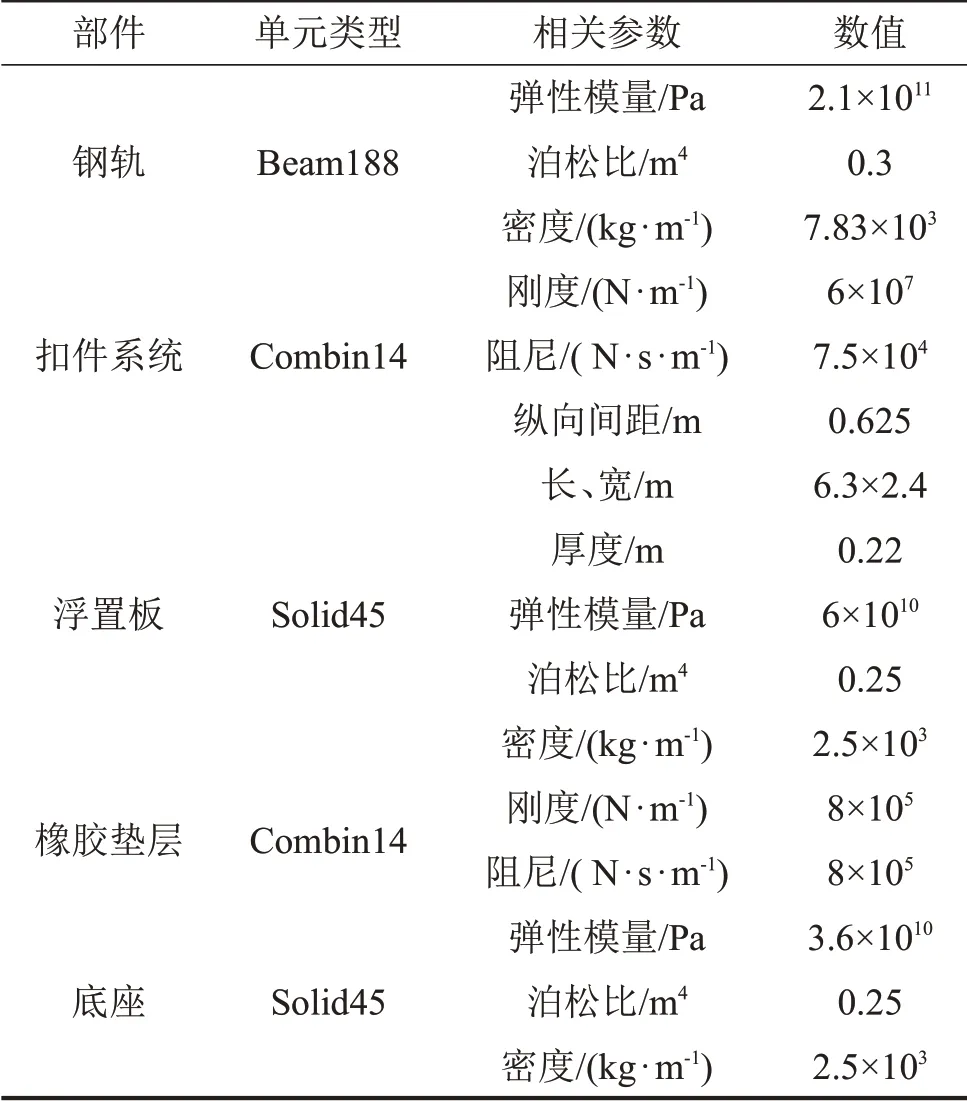
表1 橡胶浮置板减振轨道模型参数

选取时域下橡胶浮置板跨中位置处钢轨垂向位移和垂向加速度响应仿真结果如图3所示。橡胶浮置板跨中中心位置处垂向位移和垂向加速度如图4所示。车辆经过测点位置时，钢轨和浮置板产生剧烈振动，钢轨垂向位移达到1.5 mm，浮置板中心位置垂向位移达到1 mm。钢轨垂向振动加速度接近180 m/s2，浮置板中心垂向振动加速度接近22 m/s2。各项参数均符合浮置板轨道技术规范要求。

图3 钢轨垂向动力学响应

图4 橡胶浮置板垂向动力学响应

为验证上述模型的准确性，将模拟计算结果与现场实测结果进行对比，模拟仿真的工况参数与现场实测时的工况参数保持一致。现场测试的地铁线路尚处于试运营阶段，主要测试了地铁列车空载通过时轨道结构的振动响应。该线路中的地铁列车为A型车，运行速度为80 km/h，测试区段的轨道结构为橡胶浮置板减振轨道。现场测试概况如图5所示。测试中采用的主要试验设备包括：16通道网络分布式采集分析仪INV3062s，INV9824型ICP加速度传感器（量程100 g），INV9822型ICP加速度传感器（量程50 g）分别布置在钢轨轨底和轨腰处、隧道壁以及浮置板道床垂向和横向位置。

图5 实测测点位置

将实测工况参数下计算获得的橡胶浮置板振动加速度频域曲线与测试得到的橡胶浮置板振动加速度频域响应进行对比，如图6所示。计算和实测结果中橡胶浮置板振动加速度最大值出现在50 Hz～100 Hz，且实测结果与仿真结果拟合良好。

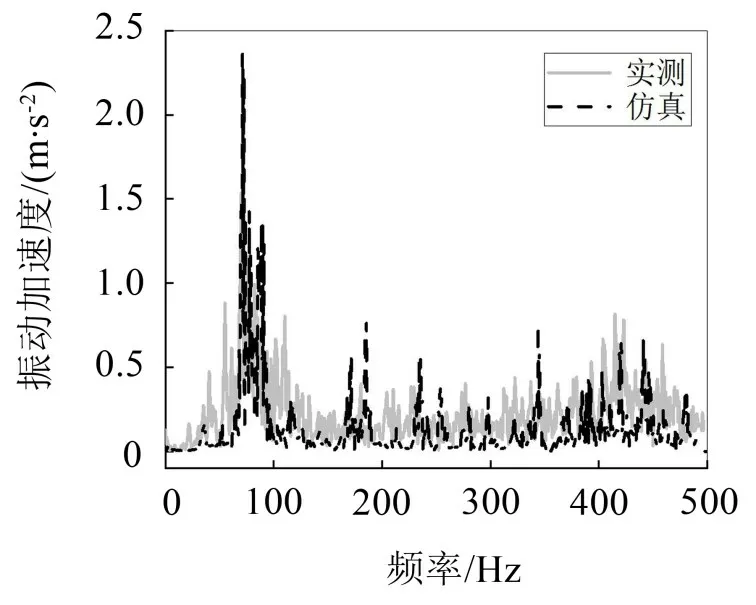
图6 浮置板振动加速度对比

通过实测结果对比，说明上述橡胶浮置板有限元分析模型能够正确模拟实际工况下橡胶浮置板减振轨道动力学响应。在下文中将对符合浮置板轨道技术规范的橡胶浮置板进行声辐射分析，考察其声振特性。

2 橡胶浮置板的结构声振特性分析

2.1 橡胶浮置板的声辐射计算模型

橡胶浮置板在自由声场中的声辐射问题符合声波在理想流体介质中的传播的条件，由于其自身的混凝土材质，振动量很小，属于小振幅线性声学波动问题。将空间任意点的边界量采用4节点等参单元插值，橡胶浮置板结构划分后形成的M个单元，将单元任意点的局部坐标设为(ξ,η)，依次将每个节点作为源点，在流体域声场中有Helmholtz积分方程：

对节点k进行插值计算代入式（1）中，并使用矩阵表示为

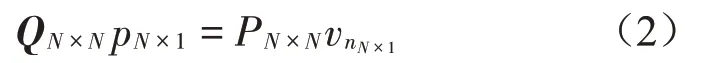
利用Helmholtz积分方程可得外声场的声压：

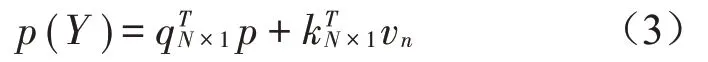
2.2 橡胶浮置板的声振特性

通过有限元-边界元方法计算获得橡胶浮置板跨中中心振动加速度频域响应如图7所示。

图7 橡胶浮置板跨中中心振动加速度

由图7可知，地铁列车通过时，橡胶浮置板发生了剧烈振动，在整个计算频段都有低于1 m/s2的小幅振动，橡胶浮置板中心位置加速度最大值出现在50 Hz～100 Hz，其最大值接近2.5 m/s2，故其主振频率为50 Hz～100 Hz。

橡胶浮置板辐射声功率反映了其自身剧烈振动进而对外进行声辐射的能力。辐射声功率越大，则声源向外辐射声波的能力越强。如图8所示。

图8 橡胶浮置板辐射声功率

由图8可见，橡胶浮置板在50 Hz～100 Hz主振频段内，辐射声功率达到最大值接近110 dB。即橡胶浮置板振动响应结果与其辐射声功率有密切关系，浮置板振动加速度幅值越大，其辐射声功率也越大。

值得注意的是橡胶浮置板辐射声功率在主振频段之外也有较大峰值，例如，171 Hz和190 Hz时，其辐射声功率最大值接近100 dB。但在图7所示橡胶浮置板加速度响应中，171 Hz和191 Hz处的加速度幅值要远小于主振频段加速度最大值。通过对橡胶浮置板振动模态进行分析发现，171 Hz和191 Hz分别为橡胶浮置板第9阶和第11阶共振发生频率。可以认为共振效应加强了橡胶浮置板的声辐射能力，故在171 Hz和190 Hz处也有较大辐射声功率峰值出现。

为更清晰探知橡胶浮置板声振特性，设置浮置板跨中位置为中心，左右各25 m，上下各10 m区域为声辐射预测声场，如图9所示。设置SF1、SF2为浮置板正上方声场测点，SF3为水平方向声场测点。计算获得各场点线性声压级如图10所示。

图9 声辐射预测声场

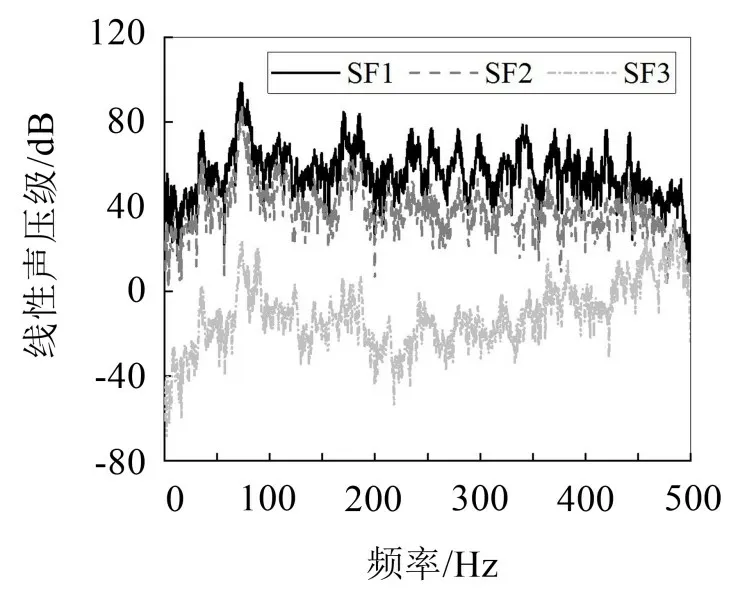
图10 线性声压级

各场点声压级最大值均出现在50 Hz～100 Hz的主振频段。SF1与SF2测点线性声压级值远大于SF3测点，即浮置板正上方声场声压值远大于水平声场声压值；SF1测点相对于SF2测点更接近浮置板位置，其线性声压级值略大于SF2测点。这是由于橡胶浮置板振动声辐射在自由声场中是沿竖直方向传播，且距声源距离越远，衰减越多，声压值越小。

距离浮置板轨道10 m高的SF2测点处的线性声压级最大值接近90 dB，表明橡胶浮置板自身振动产生的声辐射可能对车内噪声产生一定的影响。

3 橡胶浮置板的声辐射规律形式

由式（2）和式（3）可知，橡胶浮置板振动声辐射声压值的大小与其表面振速有直接关系，橡胶浮置板振型及输入参量的变化对其结构表面声压分布及外辐射声场声压分布具有重要影响。

选取几种典型的橡胶浮置板减振轨道声辐射外声场声压分布云图如图11所示。橡胶浮置板辐射外声场声压云图呈现出上下、左右相互对称的状态，这符合自由声场声辐射规律。外声场声压云图呈现浮置板正上和正下方较大，浮置板水平方向较小的趋势，这是由于浮置板垂向振动使其声波延垂向方向向外扩散造成的。橡胶浮置板声辐射规律形式大致可以分成3种描述方式：

(1)声场分布类似于理想声源在自由声场中的辐射；

(2)声场分布呈束状从橡胶浮置板声源处向外辐射；

(3)声场分布呈现复杂的混乱无序形分布。在下文中，将以上3类分布方式结合对应频率下的橡胶浮置板振动加速度云图以及声压分布云图分别讨论其声辐射特性问题。

如图11(a)所示，橡胶浮置板在35 Hz处计算得到的外声场声压分布云图类似于理想声源在自由声场中的辐射，呈现出由浮置板声源处延垂向方向均匀扩散的状态，故暂且称这种声辐射规律形式为类理想声源外声场，同样相似的声辐射规律形式还出现在72 Hz等频率处。提取35 Hz和72 Hz处振动加速度云图和声压分布云图，如图12所示。对比发现，在上述频率下的橡胶浮置板振动加速度云图，呈现出延板长方向的上下弯曲特征；而橡胶浮置板声压分布云图则根据振动加速度云图弯曲阶数延板长方向出现相应数量的圆形或椭圆形扩散。

图11 橡胶浮置板辐射外声场声压分布云图/dB

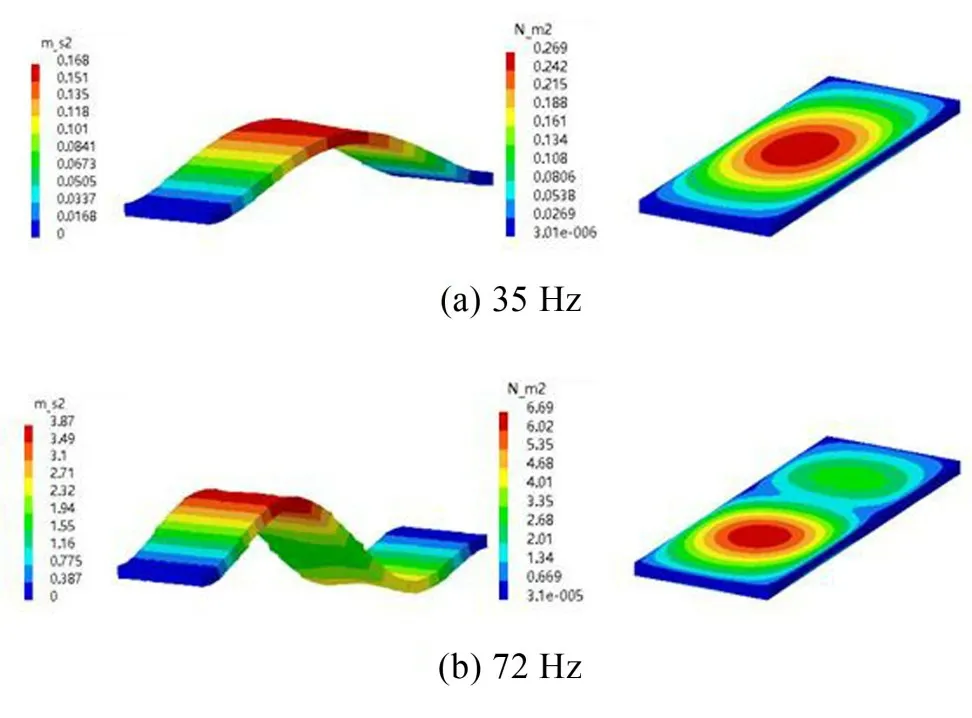
图12 浮置板振动加速度和声压分布云图

如图11(b)所示，橡胶浮置板在52 Hz计算得到的外声场声压分布云图大致呈4束由浮置板声源处向外散射的形态，4束声波的声压大小基本相同，故暂且描述这种声辐射规律形式为分束散射形外声场。提取52 Hz和相同声辐射规律形式下390 Hz处振动加速度云图和声压分布云图，如图13所示。可以发现，在上述频率下的橡胶浮置板振动加速度云图，呈现出横向弯曲特征，由于浮置板两侧约束，横向弯曲表现为延板宽方向的隆起或下凹；橡胶浮置板声压分布云图则根据振动加速度云图在隆起或下凹位置出现椭圆形扩散，当出现多阶弯曲时，由于横向间距狭窄，呈现条状分布。而浮置板跨中声场，由于有两个声强集中点向外辐射，也就产生了4束向外辐射声波。

图13 浮置板振动加速度和声压分布云图

图11(c)所示，橡胶浮置板在235 Hz频率下计算得到的外声场声压分布云图大致呈6束声波向外散射，其中浮置板正上方和正下方两束声波声压值较大，另外4束声波相对较小，这种声辐射规律形式也可归结为分束散射形外声场。如图14所示。

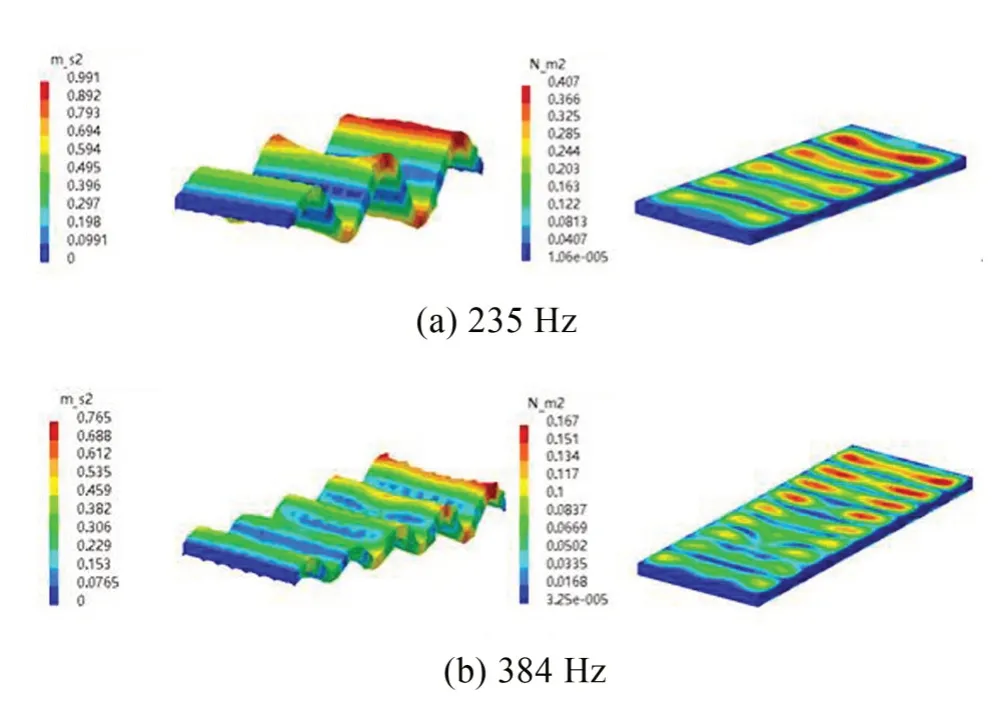
图14 浮置板振动加速度和声压分布云图

造成这种分6束辐射的原因在于浮置板声压分布云图跨中位置出现3个声压集中点，不同于图13所示的浮置板整体振动形式，在本类别的外声场声压分布对应的浮置板加速度云图呈现沿板长方向的上下弯曲叠加局部振动的形式，并且局部振动影响的范围较小，也就造成了声场分布出现大小不同的6束声波散射现象。当频率更高时，如384 Hz处，局部振动进一步加剧，但并不影响整体振型，此时橡胶浮置板会出现更多束的声波散射的现象。

图15所示，479 Hz远离橡胶浮置板主振频段，浮置板上下弯曲的整体振动形式与局部振动的大小逐渐接近，局部振动影响开始显现并接近或掩盖整体振动形式的贡献，使得浮置板声压分布逐渐呈现点状分布特征，其辐射声压场呈现出复杂的无序性分布，故暂且描述这种声辐射规律形式为复杂的混乱无序形外声场，如图11(d)所示。

图15 479 Hz处浮置板振动加速度和声压分布云图

综上所述，在较低频段，橡胶浮置板整体振动表现为较为规则的沿板长或板宽方向上的上下弯曲振动，声辐射规律形式呈现较为规则的类理想声源辐射状态；随着频率增加，浮置板局部振动影响开始显现，声辐射规律形式展现分束辐射的特征；在更高频率下，浮置板整体振动量减小，局部振动量接近或掩盖整体振动量，声辐射规律形式出现复杂的混乱无序形式。

4 结语

本文以城市轨道交通中常见的橡胶浮置板减振轨道为研究对象，采用有限元-边界元方法建立了移动载荷下车辆-橡胶浮置板减振轨道动力学模型和声学预测模型，对橡胶浮置板声辐射效率、线性声压级、声场分布等声辐射特性进行分析，研究其声振特性，得出以下3点结论：

（1）通过与实测结果对比，本文建立的橡胶浮置板减振轨道有限元模型能够很好地模拟实际工况参数下的橡胶浮置板轨道动力学响应；

（2）文中采用的橡胶浮置板的主振频率为50 Hz～100 Hz，其产生的声辐射线性声压级在浮置板上方10 m处最大值接近80 dB；

（3）橡胶浮置板减振轨道外声场主要沿垂直方向传播，其声辐射规律形式主要可描述为3种形式，即类理想声源外声场、分束散射形外声场和复杂的混乱无序形外声场。