高速列车新型车窗隔声性能研究

石广田，徐郑骁，张小安，张晓芸，杨力

（1.兰州交通大学 机电工程学院，兰州 730070；2.中铁上海设计院集团有限公司，上海 200070）

当列车以200 km/h以上的速度运行时，噪声污染问题将同列车安全性、牵引动力等因素一起限制高速列车的进一步提速[1]。当前研究多集中于高速列车板材隔声问题的研究[2-5]。列车车窗区域作为噪声敏感区域[6]，目前对于其研究主要针对普通车窗，如张玉梅等[7]建立高速列车双板空腔结构车窗隔声量计算模型研究了车窗厚度、空腔厚度和空腔阻尼对车窗隔声量的影响，刘继生等[8]从隔声机理角度比较了现用铁路客车车窗玻璃中单层钢化玻璃、钢化中空玻璃和夹层中空玻璃3种结构形式对隔声效果的影响。此外徐振骁[9]开展了高速列车常用车窗玻璃的隔声性能研究。对于真空车窗玻璃与智能车窗玻璃（电致变色车窗玻璃）却鲜有研究，所以对于新型列车车窗的隔声性能研究是很有必要的。本文通过建立更符合高速列车运行环境的声学计算模型，计算真空车窗玻璃的隔声性能曲线，分析其声桥长度、外板厚度以及真空度对其隔声性能的影响，并对其各自影响规律进行对比总结；以北京航空航天大学电致变色中心某型电致变色玻璃为例，计算电致变色车窗玻璃的隔声性能曲线，分析其总隔声量随软膜厚度变化的规律。将两类新型车窗玻璃的隔声性能曲线与现有高速列车车窗玻璃隔声性能曲线进行对比，说明其声学性能在不同频段或不同情况下的优劣势，对高速列车车窗玻璃选型与改进有一定的实用价值。

1 声学计算模型

在列车实际运行中，内部的声场是有限的空间，而外部的声场是接近无限的空间，参照实际情况，建立外部的空间较大的混响室，内部按照高速列车内部空间参数建立消声室。建立如下图1所示的高速列车车窗玻璃声学计算模型：

图1 高速列车车窗玻璃声学计算模型

对真空玻璃进行声学建模时，其中间真空层的声桥为较小的杆状结构，杆件结构的振动模态密度分别用弯曲波数KB、圆频率ω以及赫兹频率f来表示如式(1)所示。

式中：N为模态数，l为中间声桥的物理长度，CB为波速参数。即真空车窗玻璃中间的声桥结构的模态密度与其边界条件无关。当圆频率ω发生变化时弯曲波速CB也会随之变化，这种现象称之为频散现象。弯曲波虽然会出现频散现象使原波形发生一定的改变，但是无论机器的疲劳故障或是人的耳朵对如此较小的波形细节的差异变化感知十分微弱。但是频散现象能够对振型数和模态密度产生影响[10]。

真空车窗玻璃外部为板件结构，其振动模态密度分别用弯曲波数KB、圆频率ω以及赫兹频率f来表示如式(2)所示。

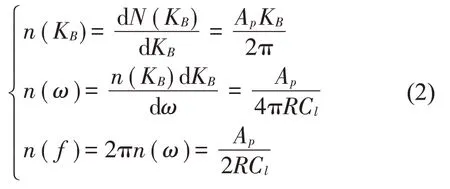
式中：Ap为平板的表面积，R是平板截面的回转半径，Cl即为波速参数。由上式(2)可知，当平板的表面积越大，或平板的厚度越小，则板间的模态密度越大。

进行统计能量法（SEA）计算时，统计能量分析的子系统必须要求其子系统内能够储存振动能量[10]。而只有当一定数量的相似共振模态所组成的一组或一群能够实现共振运动的子系统才可以储存振动能量。这样的一群或一组相似模态在统计能量分析中就可以视为一个统计能量子系统。一个SEA子系统在目标带宽内的模态数，与其子系统的特性参数，即模态密度有着直接关系。目前的统计能量计算具有低模态密度的子系统的耦合动力学问题时，计算精度并不高。而在式(1)和式(2)中，声桥杆件的模态密度较低，真空车窗玻璃外板件的模态密度较高，所以为了提升计算精度，在对声桥影响下真空车窗玻璃隔声性能计算采用有限元-统计能量法（FE-SEA）混合计算方法。FE-SEA混合模型前处理如图2所示。

图2 FE-SEA混合模型前处理

由于声桥在振动时与外板相连，故对真空玻璃声桥的声振模态进行计算时不能仅仅计算柱形声桥的自由模态，而需要对声桥在真空外板的约束下的声振模态信息进行求解。求解前，将真空外板用较大网格进行划分，而对声桥结构则采用更为精密的网格，并检查整体网格质量，进行计算。求解模态结果如图3所示（以前4阶为例）。

图3 真空车窗玻璃模态图

将模态计算结果导入VA One中，生成有限元（FE）子系统模型，将有限元子系统模型与外部SEA板件相连接，将FE声桥子系统SEA外板子系统与内外侧声腔相连接，实现声能传递，FE-SEA混合模型如图4所示。

图4 真空车窗玻璃FE-SEA混合模型

2 隔声性能计算

依据上节声学计算模型，分别计算真空车窗玻璃的声桥长度属性、板件厚度属性以及真空度属性对其隔声性能的影响；并对电致变色车窗玻璃的隔声性能进行计算分析。

2.1 不同声桥长度计算

真空腔内的中空声桥结构不仅支撑着中空车窗玻璃的外侧板件，还具有声能传递的功能。故当真空车窗玻璃的真空腔内声桥长度发生变化时，其隔声量也势必发生改变。本小节中采用控制变量的方法对真空玻璃真空腔内声桥长度与隔声量的变化关系进行研究。选用真空玻璃的真空介质压强为5 000 Pa保持不变，真空腔两侧的玻璃外板厚度保持不变，中间声腔长度选为5 mm～30 mm（变化步长为5 mm）。将各个子系统同内外侧声腔进行连接，实现能量传递。计算结果如图5所示。

图5 真空声桥长度变化隔声量对比图

如图5计算结果，当真空车窗玻璃的声桥长度发生变化时，其隔声量总体有所增加。声桥长度增加，其隔声量的增加在个别频段并不十分明显。当声桥长度由5 mm变化至25 mm时，真空车窗玻璃在中低频的隔声量虽然有所增加，但是增幅并不明显，当真空声桥长度增加至30 mm时，真空车窗玻璃在低频段的隔声量有较大的增幅。在高频段，随着声桥长度的增加，真空车窗玻璃的隔声量基本在全部的频段都随之增加但增幅较小。

随着声桥长度的增加，隔声量也随着增加。但是实际生产和使用时并不能无限制地增加声桥长度来增强其隔声量。当声桥长度每增加1 mm时，其总隔声量随之变化的增值大小能够评判其总隔声量随厚度的变化速率，对真空玻璃声桥长度的选择具有参考意义，也能更直观地考察其对总隔声量增值的贡献效率。即长度每增加1 mm所带来的总隔声量增值越大，其隔声性能的经济适用型就越高。真空声桥长度为5 mm～30 mm区间内，真空车窗玻璃总隔声量随厚度变化增速如图6所示。

如图6计算结果，当真空车窗声桥长度变化区间为5 mm～30 mm时，其总隔声量一直在增加，但是增速随着厚度的增加逐渐变小。所以单纯通过增加真空玻璃声桥长度来增强其隔声性能是不可取的。

图6 总隔声量增速与长度关系图

2.2 不同板件厚度计算

当真空车窗玻璃的两侧玻璃板件的厚度发生变化时，其隔声量也势必发生改变。本小节中采用控制变量的方法对真空玻璃面板厚度与隔声量的变化关系进行研究。选用真空玻璃的真空介质压强为5 000 Pa保持不变，真空腔的厚度设置为30 mm且保持不变，一侧玻璃板件厚度为8 mm且保持不变，另一侧厚度选为6 mm～16 mm的相同玻璃板件（变化步长为2 mm）。将各个子系统同内外侧声腔进行连接，实现能量传递。隔声性能曲线结果如图7所示所示。

图7 不同厚度真空玻璃隔声曲线

当真空板件厚度由6 mm增加到16 mm过程中，随着厚度的增加，真空车窗玻璃在低频的隔声量有所增加，但在中频段的增值并不十分明显；在中高频段出现隔声低谷时，其增量十分有限；在高频区段可以很明显看出随着厚度的增加，真空车窗玻璃的隔声性能有所增加。如图8所示，当真空车窗玻璃板件厚度变化区间为6 mm～16 mm时，其总隔声量一直在增加，但是其增速随着厚度的增加逐渐变小。与声桥长度变化而引起的总隔声量变化幅值相比，板件厚度变化所引起的总隔声量变化幅值较大，即板件厚度对于真空车窗玻璃隔声性能的影响要强于声桥长度。

图8 总隔声量增速与厚度关系图

2.3 不同真空度计算

对不同真空度的真空车窗玻璃进行隔声性能计算时，将中间所处于真空环境下的气体介质作为一个SEA子系统进行建模。当气体介质处于真空环境下时，其密度属性，分子与分子或分子与其他粒子之间的作用力以及碰撞属性发生变化。即在进行统计能量法声能计算时，根据子系统间功率流平衡方程，介质所对应的能量损耗矩阵（包含子系统的内损耗因子以及子系统间的耦合损耗因子）发生改变，故对其真空度发生改变时，其隔声量会随之发生变化。以空气介质为例，当气体介质所处压强发生变化时，其本身气体属性会发生变化，本节中对4组真空度进行真空车窗玻璃隔声量计算，真空度分别为90 000 Pa，40 000 Pa，20 000 Pa和5 000 Pa。真空介质的声学参数设置如表1所示。

表1 不同真空度气体参数表

当真空度发生改变时，气体介质改变的参数以气体介质的密度尤为明显，声速以及运动黏度的变化十分微小，声速参数随着上述真空度变化的变化数量级处于1.0×10-3等级，运动黏度参数随着上述真空度变化的变化数量级处于1.0×10-7等级。依据上述参数对真空SEA声腔进行属性设置，真空玻璃的板件厚度保持不变，且真空层的厚度保持不变，计算如表1所示4种真空度下的真空车窗玻璃隔声量（分别设置4种真空腔的压力为：90 000 Pa、40 000 Pa、20 000 Pa、5 000 Pa，并进行比较，结果如图9所示。

图9中，当真空度增加时，即气体压强变小时，真空玻璃的隔声量随之增加，且随着真空度的增加，真空车窗玻璃的隔声量在全部频段都会增加，不会出现增加板件厚度或者增加薄膜结构时出现的隔声低谷的交叉现象。如图10所示。当真空度由90 000 Pa变化到5 000 Pa时，其在各个区间的总隔声量增速是不一样的，真空度由90 000 Pa变化到40 000 Pa区间中，其总隔声量的增速要小于真空度在40 000 Pa至20 000 Pa的增速，当真空度由20 000 Pa向5 000 Pa变化时，其气体介质压强每增加1 000 Pa，隔声量增速大幅增加。即真空玻璃的真空度由小到大变化时，其隔声量不仅有增加的趋势，其隔声量的增幅也随着真空度的增加而增加。声波的传递需要传播介质的参与，理想真空状态时声波是无法传递的，故真空度在20 000 Pa至5 000 Pa接近理想真空，总隔声量增值出现急剧变化。

图9 不同真空度车窗玻璃隔声曲线

图10 总隔声量增速与真空度关系图

2.4 电致变色车窗玻璃隔声性能计算

电致变色软膜车窗玻璃是将玻璃中加上一层具有电致变色功能的镀层结构。在声学计算中常常通过增加阻尼层来降低振动的幅值，从而实现更好的隔声效果，所以电致变色膜结构减小玻璃板件振动幅值是切实可行的。本节对于电致变色镀层的结构损耗因子进行分析，以研究其对隔声性能的影响。

ηis是子系统i结构材料（内摩擦、滞后或黏弹性）特性的函数，结构的振动能量E(E=Pd/ωη)与阻尼损耗因子成反比，所以增大结构损耗因子能够降低振动的幅值。如原结构子系统的ηis为0.01的数量级，若在其原结构子系统的表面覆盖层状阻尼材料，甚至能够使结构子系统的ηis达到0.1的数量级[12]。此时能够使结构子系统的振幅降低。以北京航空航天大学电致变色中心某型电致变色玻璃为例，电致变色软膜的阻尼损耗因子区间如图11所示。

图11 常用材料弹性模量与损耗因子

目前的电致变色玻璃，其电致变色镀膜的厚度都较小，在这里选用电致变色膜结构的厚度为0.1 mm，即声学模型的物理厚度参数为：6 mm+0.1 mm+10 mm。改变其阻尼损耗因子参数，选用具有代表性的η=0.01、η=0.1、η=1三组阻尼参数进行电致变色车窗玻璃的隔声量计算，结果如图12所示。

图12 不同阻尼电致变色车窗玻璃隔声曲线

根据计算结果如图12所示。可以看出当膜结构的阻尼损耗因子η=0.01、η=0.1时，这两种软膜对于隔声量影响远弱于阻尼损耗因子η=1的软膜，尤其是在高频段的改善更为优异。

将电致变色软膜的厚度改变分别取厚度为0.1 mm～1 mm（变化步长为0.1 mm），对其隔声量曲线进行计算，计算结果如图13所示（以η=0.1为例），分析其总隔声量随厚度变化的变化速率如图14所示。

图13 不同厚度软膜隔声曲线

图14 总隔声量增速与厚度关系图

当电致变色膜结构的厚度发生变化时，如图13所示。随着厚度的增加其隔声量随之增加，但在低频段的变化并不十分明显，隔声量的增值主要出现在高频区段。

如图14所示当电致变色车窗玻璃的镀层阻尼损耗因子η=0.1、η=1时，增加单位厚度的镀膜，其隔声量的提升不同。当阻尼损耗因子η=1时，增加0.1 mm厚度的镀膜，其隔声量的增值要大于阻尼损耗因子η=0.1的电致变色玻璃，且增值并不是随着厚度增加而成正比。当阻尼损耗因子η=0.1、η=1时，其隔声量增速随着软膜厚度的增加有下降趋势。

2.5 隔声性能对比

选取两组空腔厚度（20 mm、30 mm），对相同厚度属性的真空车窗玻璃（选用不同真空度属性）与中空车窗玻璃的隔声量曲线进行对比，如图15所示。

图15 真空-中空隔声曲线对比图

图15（a）、图15（b）为空腔厚度为20 mm、30 mm的中空车窗玻璃与真空车窗玻璃隔声量曲线对比图。当空腔厚度属性由20 mm变化至30 mm时，中空以及真空车窗玻璃的整体隔声趋势并没有发生明显变化，且中空车窗玻璃的整体隔声量增值十分有限。真空度较低的真空玻璃（如图中真空度为90 000 Pa）其隔声性能在低频段的隔声性能甚至弱于相同厚度的中空玻璃，但是在高频段的隔声性能明显优于相同厚度的中空玻璃。真空车窗玻璃的真空度增加，其隔声性能优于相同厚度的中空玻璃。

选用北京航空航天大学电致变色实验中心的某型电致变色软膜玻璃为例，根据实验中心实物相关参数，对带有电致变色软膜的车窗玻璃进行声学建模计算（以软膜厚度为0.5 mm的电致变色车窗玻璃为例）其隔声量曲线与相同厚度PVB夹片对比如图16所示。

由图16计算结果，某型电致变色软膜车窗玻璃的隔声性能与电致变色镀膜略有不同，当电致变色镀膜玻璃在中低频段的隔声性能与相同厚度PVB膜类似，只是在高频区段有所差别；但是电致变色软膜玻璃与相同厚度的PVB夹层玻璃相比，在低频和部分中频段，其隔声性能要略低于PVB夹层玻璃，但是在高频段可以看出某型电致变色软膜玻璃的隔声性能要比相同厚度的PVB夹层玻璃具有更好的表现。

图16 电致变色-PVB车窗隔声曲线对比图

3 结语

(1)真空车窗玻璃的隔声性能随着声桥长度、板件厚度的增加而增加，但总隔声量的增速随着长度、厚度的增加呈下降趋势；

(2)真空车窗玻璃的隔声性能随着真空度的增加而增加，但总隔声量的增速随着真空度的增加呈下降趋势，对真空车窗玻璃隔声性能影响最大的因素为真空度；

(3)真空车窗玻璃在真空度较低时，其隔声性能在低频段弱于相同厚度中空车窗玻璃，但真空度较高时，其隔声性能大幅提高；

(4)电致变色软膜厚度增加，隔声性能随之增加，在高频段尤为明显，现有电致变色软膜车窗在高频段相较于PVB车窗拥有更好的隔声性能。