STFT-IP时频特征提取技术的螺栓松动识别方法
王九龙,盛俊杰,蒋家勇,温金鹏,肖世富,张周锁
(1.中国工程物理研究院 总体工程研究所,四川 绵阳 621999;2.西安交通大学 机械工程学院,西安 710049)
螺栓联接作为简单有效的联接方式之一,具备安装简单、拆卸方便、成本低廉等优点,因此被广泛应用于航空航天、交通运输、化工等行业。由于实际工况的复杂性和不确定性,螺栓联接结构经常会面临恶劣的工作环境,长期承受交变负载带来的振动、冲击和疲劳。从而导致螺栓连接结构出现松动甚至脱落,影响整个机械设备正常运转,严重时还会造成重大的经济损失和人员伤亡。因此,建立可靠有效的螺栓预紧状态监测手段具有重要的工程意义。
按照检测原理划分,目前常用的螺栓松动检测方法包括基于经验观察和直接测量的方法、基于声学检测的方法、基于结构振动特征识别的方法和基于压电阻抗(EMI)的监测技术。其中通过划线观察和扭矩扳手测量的方式最为简单直观,但是对于复杂结构难以操作,且测量精度有限。此外,有学者提出了基于应变的螺栓预紧力测试手段,通过螺栓应变间接测量螺栓轴向预紧力,但是该方式受螺栓安装形式和传感器布置限制[1]。还有学者提出利用声波监测螺栓预紧状态,包括声发射原理和超声波等,具有较高的测量效率和精度,但是精密仪器容易受环境干扰[2-4]。基于压电阻抗技术的方法也被广泛应用于螺栓状态监测,该方法可对微小变形、裂纹敏感,可实现螺栓松动的早期监测,但是压电片和主体结构的耦合导致阻抗计算模型十分复杂[5-7]。而结构振动响应包含丰富的螺栓连接结构状态信息,因此大量学者还提出了基于结构振动响应的松动识别方法,通过分析振动响应中的阻尼、固有频率模态参数,或提取不同预紧状态下的小波包能量特征和功率谱特征等,实现螺栓松动识别[8-11]。
现有的基于结构振动响应的螺栓松动识别技术多通过直接提取振动响应的模态参数、时域特征或频率特征,往往忽略了振动响应中丰富的时频特征。基于此,本文以振动响应作为切入点,提出了基于时频特征的螺栓松动识别方法,综合考虑响应信号在时域尺度与频域尺度的特征,并结合试验对所提时频方法与传统方法进行对比,验证其辨识螺栓连接结构状态的有效性和精度。
1 时频图特征分析
区分于经典的信号相关分析、时域平均技术、傅里叶变换等时域分析技术和频域分析技术,时频分析方法结合了时域和频域分析的特点,既可以观察到信号在时域尺度上的特征,又可以同时分析频率成分随时间的变化。比较常用的时频分析方法包括STFT变换、小波变换、Gabor变换等。其中STFT是在傅里叶变换基础上提出的,在傅里叶变换过程加一个滑移窗函数,利用窗函数大小控制变换结果的时域分辨率和频率分辨率,其表达式如下:

式中:t和f表示时间和频率,x(τ)表示待分析的信号,h*(τ-t)表示滑移窗函数的共轭函数。
本文在短时傅里叶变换原理基础上,结合图像处理技术,提出新的时频特征提取方法来表征螺栓连接结构预紧状态。下面结合具体的实验信号引出该时频指标。图1是某螺栓连接结构在拧紧力矩为2 N·m和20 N·m状态下的瞬态冲击响应(具体实验在第三章详述),从图1可看出,除响应幅值存在差异外(力锤激励输入存在差异),难以直接从响应信号中提取到其他敏感特征。
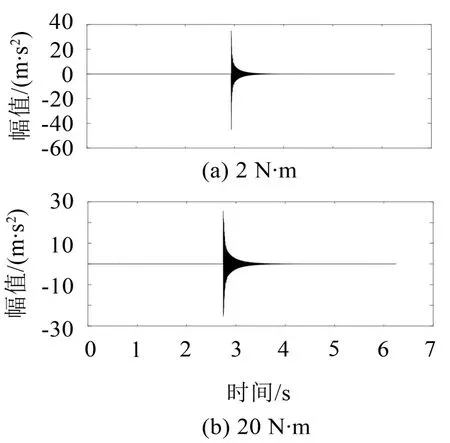
图1 加速度响应信号
对图1所述两个响应信号作STFT变换,其时频图如图2和图3所示。

图2 短时傅里叶变换(2 N·m)

图3 短时傅里叶变换(20 N·m)
从图中可看出,2 N·m和20 N·m拧紧力矩状态下的瞬态冲击响应低频特征和高频特征均存在差异。在低频特征中,两种响应频率成分组成相同,其主要差异表现在时间尺度上衰减速度不同,在2 N·m拧紧力矩状态下,其低频成分衰减更快。同时,与20 N·m拧紧力矩状态下的振动信号时频响应不同,在2 N·m拧紧力矩状态下,有部分高频成分被激发出来。
综合上述分析结果可知,螺栓连接结构在预紧状态不同时,其低频特征和高频特征均存在差异,STFT变换可有效表征其在时域尺度与频域尺度的特点,因此,准确定位并提取时频特征,就能实现螺栓连接结构的预紧状态评估。围绕如何量化时频差异并建立其与螺栓预紧状态的映射关系,本文提出了基于STFT变换与图像处理技术结合的螺栓松动识别方法,建立了STFT-IP松动特征指标。
2 STFT-IP时频特征提取方法
本文所提的STFT-IP时频特征提取方法流程如图4所示。主要步骤由两部分组成,首先通过STFT变换得到振动响应信号在不同时间点下的频率分布。然后结合图像处理技术,对STFT时频特征进行量化,核心思想是通过建立STFT-IP指标,对比不同预紧状态下的指标差异,实现螺栓连接结构预紧状态评估。详细步骤见图4。

图4 STFT-IP时频特征提取方法流程
(1)对螺栓连接结构作力锤模态测试,得到其振动响应信号。首先对振动信号时域图进行初步分析,在此基础上统一不同预紧状态下时频特征初始值,对振动信号进行截取,定义其截取范围为[a,b],起始点a取振动响应极值点,终止点b的选取需满足截取范围能基本涵盖振动响应的整个衰减过程。
(2)对截取信号作STFT变换,得到振动响应信号的时频图,根据不同的时频分布特征可初步区分不同螺栓预紧状态,但要建立时频特征与预紧状态的映射关系,还需对特征指标进一步量化。
(3)由于力锤敲击的初始激励大小不同,因此不同响应信号的时频特征幅值衡量标准存在差异,同时为进一步简化计算和突出细节差异,将STFT时频图看成时频矩阵,对矩阵进行二值化处理,得到不同时间点与频率点下的IP指标,具体计算如下式:

式中:i表示时间点,N表示时间点数量;j表示频率点,K表示频率点数量;STFT(i,j)表示STFT时频矩阵初始值;m表示STFT时频矩阵均值。
(4)将STFT-IP矩阵按行或按列生成STFT-IP序列(向量),取螺栓预紧结构初始状态下的STFT-IP序列为基准序列X0=[x,x02,…,x0N×K],其他序列为对比序列Xm=[x,xd2,…,xdN×K]。
(5)计算对比序列与基准序列的欧式距离,通过欧式距离大小评估螺栓预紧结构松动状态,具体计算公式见下式:
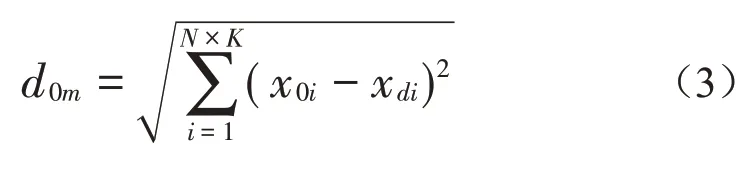
3 实验验证
3.1 实验介绍
为验证所提基于STFT-IP时频特征提取技术的有效性,建立了如图5所示的试验台。该试验系统的两根梁通过两个M8的六角头螺栓连接,上梁通过2根绳子悬挂,在上梁与下梁上各安装一个加速度传感器,通过信号处理预分析,上方传感器所接收信号更为敏感,因此本文中数据均来自于上方传感器。激励方式通过力锤施加,测试该结构的瞬态冲击响应,采样频率Fs为20 480 Hz。在试验过程中,设置两个螺栓拧紧力矩相等,从2 N·m开始,以2 N·m的间距一直增加到20 N·m。
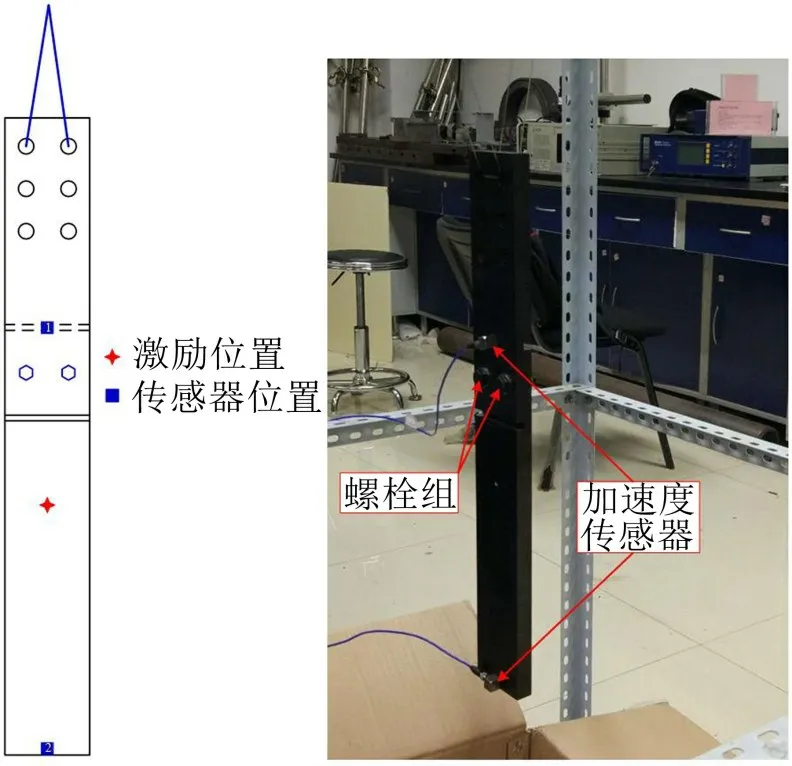
图5 螺栓连接结构试验台
3.2 螺栓松动识别
首先对20 N·m拧紧力矩状态下振动响应时域信号进行初步分析,如图6所示。根据响应信号的衰减幅度和速度,以极值点作为起始点,截取1倍采样频率长度作为基准信号,保证基准信号能涵盖整个响应衰减过程。为保持一致,对其他预紧状态下的振动响应作相同截取操作。
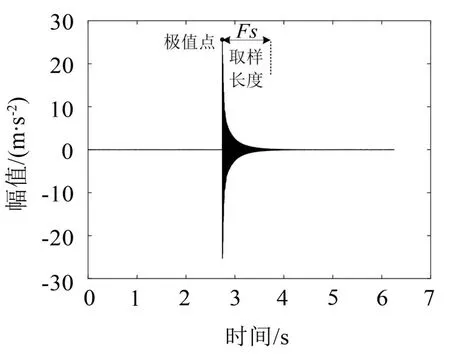
图6 时域信号(20 N·m)
在保证不同预紧状态下的振动响应信号时间尺度一致基础上,对其作STFT变换,得到不同螺栓连接结构状态的时频分布,如图7所示。从时频图发现,不同预紧状态的时频分布大致相同,细节差异难以直接定位并提取。

图7 不同预紧状态下的时频图
为进一步量化时频特征并凸显细节差异,同时消除由力锤激励大小不同带来的幅值差异,对时频图进一步作二值化处理,得到STFT-IP时频特征矩阵,见图8所示。从图8中可发现,在二值化处理后,STFT-IP时频特征细节差异更为凸显,包括频率成分分布和时间尺度的衰减。

图8 STFT-IP特征
根据二值化时频矩阵,将其按行排列进一步简化为STFT-IP特征序列,不同序列的片段对比图如图9所示。

图9 STFT-IP特征序列
计算不同特征序列与基准序列之间的STFT-IP指标欧式距离,将其作为预紧评估指标,同时与常用的时域、频域指标进行对比分析,为便于衡量不同指标与拧紧力矩之间的关联性,可将所有指标进行归一化处理[12]。
图10和图11分别展示了所提STFT-IP指标与典型时域指标和频域指标的对比,由图可发现,不同STFT-IP时频特征指标的欧式距离较好的表征和区分了不同预紧状态,当拧紧力矩下降时,欧式距离逐步上升,表明其预紧状态与初始状态差距也随之增大。而常用的时域指标和频域指标与拧紧力矩之间无明显的相关性,虽有部分时域指标(均方根值和峭度指标)和频域指标(频谱重心)随拧紧力矩下降呈整体上升趋势,但是其变化波动较大,不具备严格的单调递增性。

图10 时域指标对比

图11 频域指标对比
针对某些复杂结构或特殊装备应用场景,在设备运行过程中不具备在线监测条件,可在设备暂停间隙或大修期间,基于模态测试的手段,对螺栓预紧结构进行快速维护检测。为使所提时频特征提取技术具备可实施性,利用指数函数,对STFT-IP指标欧式距离与拧紧力矩进行曲线拟合,拟合曲线见图12,拟合公式见式(4)。

图12 特征拟合曲线

式中:ST表示STFT-IP指标欧式距离,T表示拧紧力矩。
4 结语
目前常用的基于振动信号的螺栓松动状态识别技术多单独聚焦于时域特征或频域特征,往往忽略了振动响应中丰富的时频信息。基于此,本文通过短时傅里叶变换初步分析了不同预紧状态下螺栓结构的时频分布特点,结合图像处理技术提出了基于STFT-IP时频特征的螺栓松动识别方法。利用实验数据验证了所提STFT-IP时频指标表征和区分螺栓连接结构预紧状态的有效性,并通过指数函数对特征指标与拧紧力矩之间的映射关系进行了拟合,为螺栓连接结构预紧状态识别提供了新的技术途径,具有一定的工程应用价值。

