乘用车振动舒适性评价及预测

王生昌, 胡慧敏,刘 丹, 蔡凤田, 杨泽中

(1.长安大学 汽车学院,陕西 西安 710064;2.运输车辆运行安全技术交通行业重点实验室,北京 100088)

0 引言

在汽车产业迅速发展的今天，为了有更好的驾驶及乘坐体验，消费者对汽车振动舒适性的要求日益提高。具有良好振动舒适性的车辆可以减少驾驶员和乘员的疲劳，保障行车安全，延长使用寿命，提高汽车生产厂商的竞争力，因此对汽车的振动舒适性进行有效的预测及评价非常必要。目前用于汽车性能评价的方法有：依赖于道路试验和评价人员的主观评价、对有关数据进行测试分析的客观评价及通过仿真软件对性能指标进行仿真研究的计算机仿真[1]。主观评价可以准确地反映车内人员的直观感受，但评价结果受评车师个体差异的影响较大，不确定性强。客观评价与计算机仿真以测量参数作为评价依据，可以获得评价人员不易察觉到的信息，但无法表达行车过程中“人”的相关感觉。故拟建立评价预测模型，用客观试验数据预测主观评价得分，结合主、客观评价来进行振动舒适性评价，使评价结果更可靠。

Ash[2]采用神经网络模型研究主客观评价之间的关系，并讨论了如何运用评价结果来进行车辆设计改进。Valasek等[3]选取多辆乘用车进行主、客观评价的相关试验，进而研究了汽车振动舒适性主客观评价的相关性。Maeda[4]对ISO 2631-1标准的局限性进行研究，并给出了如何在振动环境下结合乘车人的振感体验进行主观试验。Pennati等[5]选取不同的受试人员进行加速度测量试验，建立了能拟合车辆座椅传递到人体的加速度模型，并构建了机械模型用于车辆舒适性评估。杜子学[6]提出了综合速度、路面状况等因素于一体的汽车综合振动舒适度指标对汽车平顺性进行分析与评价。唐荣江[7]利用神经网络建立了汽车振动舒适性客观测量参数与主观评价之间的关系，并建立了振动舒适性评价系统。龙江[8]通过体压试验对座椅舒适性进行主观评价并进行体压分布测试，利用改进后的BP神经网络建立了舒适性预测模型，模型预测结果较好。

本研究分别运用支持向量机和BP神经网络，基于试验数据建立舒适性预测模型。首先利用灰色关联度分析对影响乘用车振动舒适性的因素进行预处理，找到影响主观得分的主要因素，再分别利用支持向量机和BP神经网络建立舒适性得分预测模型，比较两模型的预测精度，找到更适用于舒适性预测的模型。

1 评价体系

1.1 主观评价体系

为对试验车振动舒适性进行全面评价，选取上下起伏、侧倾晃动等10个具有代表性的评价指标作为主观评价指标，依据各指标评价内容来对试验车进行打分和评价[9-10]，见表1。

表1 主观评价指标

主观评价打分采取满分10分制，打分间隔为0.25分，提高了评价精确度[11]。试验车舒适性越好，得分越高，评分人员为专业评车师。

1.2 客观测量指标

2 试验及试验结果

2.1 试验准备

选取配置不同的7辆乘用车(记为P1，P2，P3，P4，P5，P6，P7)，记录车辆的基本参数并进行主观评价和客观评价试验，测取客观评价参数，对车辆进行主观打分。

2.1.1 试验人员

由1名经验丰富的评车师和5名随车人员组成试验团队进行乘用车振动舒适性主、客观评价试验。评车师安全地驾驶试验车以不同的试验车速行驶来完成主、客观评价试验，根据主观评分依据对试验车进行打分。随车人员主要负责试验仪器拆、装和记录试验数据等工作。

2.1.2 试验仪器

乘用车振动舒适性客观评价试验过程中采用的试验仪器包括2个脉冲试验用凸块、1个DEWETRON数据采集仪和美国PCB公司的3个压电式加速度传感器。表2为三轴向加速度传感器的主要技术参数。

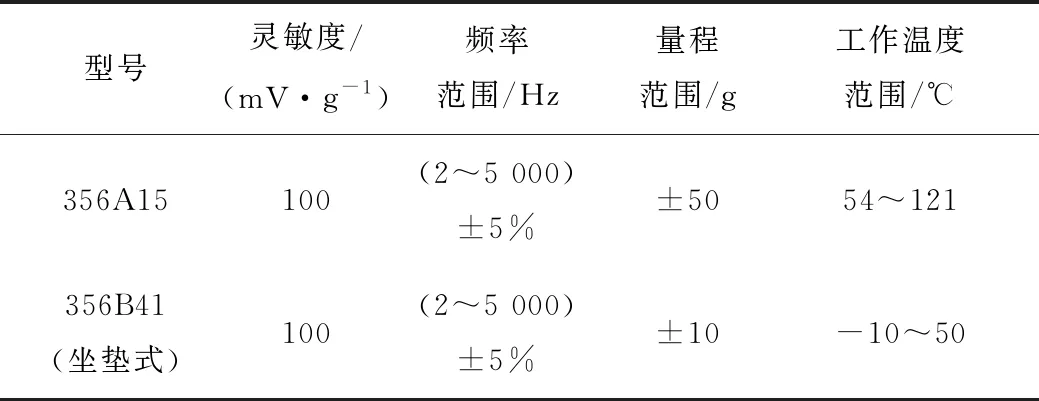
表2 加速度传感器技术参数

2.1.3 客观评价试验

随机输入试验车速为40, 50,…,90 km/h，试验路段选取试验场内平坦的干燥沥青路。进行该试验时，驾驶员驾驶试验车分别以试验车速匀速驶过试验路段。

脉冲输入试验车速为10, 20,…,60 km/h。进行该试验时，驾驶员驾驶试验车分别以试验车速匀速前进，使得同一车轴两侧的车轮同时接触垂直放置在车辆前方的凸块，匀速驶过凸块。

2.1.4 主观评价试验

在客观评价试验的基础上进行车辆全油门加速试验作为主观评价试验。全油门加速行驶时，试验车以正常行驶状态加速到60 km/h并保持5 s之后，驾驶员急踩油门踏板，全油门加速至120 km/h后松开加速踏板。试验时，将车速偏差控制在±4%以内。

为保证数据的可靠性，客观评价试验和主观评价试验中每个车速的试验进行5次，取5次测量数据的均值作为最终数据。

2.1.5 试验注意事项

为保证试验安全和试验结果的准确性，试验前调整试验车轮胎气压至标准状态，试验时车辆满载，并且要将载物固定避免其在车内晃动。乘员以日常乘车姿势倚靠在座椅上，双手放置在大腿上方。驾驶员根据自己的驾驶方式驾驶车辆，避免坐姿变化。

2.2 试验结果

2.2.1 主观试验结果

主观评价试验之后，评车师根据行车过程中驾驶及乘坐感受对车辆的各指标进行打分，给出每辆车的总得分和评语，车辆主观评价得分见表3。

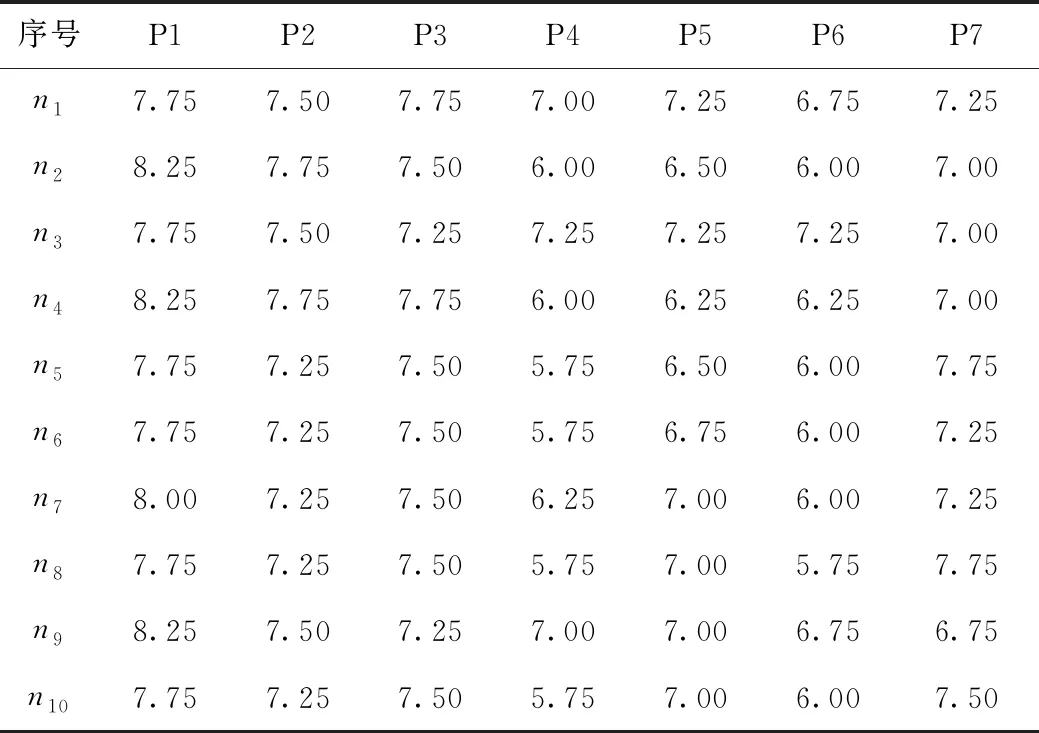
表3 各指标主观得分

试验过程中，试验车P1的前后车轮驶过凸块时，振感基本一致，比较平稳;车辆振动迅速衰减，乘员基本没有出现不适感，振动舒适性好。试验车P2和P3乘坐体验相似，车辆驶过凸块时无强烈振动，较为平稳，振动舒适性较好。试验车P4年代稍长，存在悬架等部件老化的情况，故行驶过程中减振效果差，车辆驶过凸块时出现了悬架打顶和打底现象，冲击加强，振动明显增大，乘车体验整体较差。试验车P5悬架偏硬，路感较强，车身易出现共振现象，驶过凸块时振感明显，影响乘坐舒适性。试验车P6振动衰减比其他车辆较为缓慢，驶过凸块时冲击力较大，乘坐体验一般。试验车P7是SUV车型，悬架侧重于舒适性，冲击强度适中，车身较平稳，乘坐体验一般偏好。

熵值法[15]可以判断某个指标的离散性，根据各个指标提供信息量所占的比例来确定其权重，能够排除主观因素对权重指标确定的影响。本研究利用熵值法计算乘用车振动舒适性主观评价各指标的权重，并结合各指标主观得分计算出试验车辆主观评价总得分，分别见表4、表5。

表4 各指标权重

表5 试验车主观评价总得分

2.2.2 客观测量数据

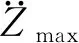
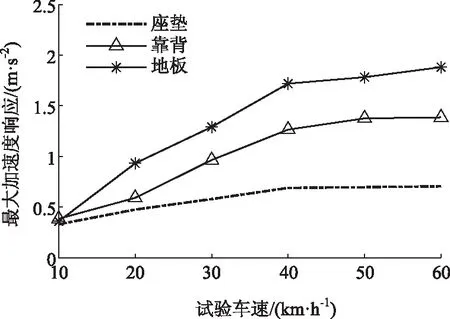
图1 最大加速度响应与试验车速的关系Fig.1 Relationship between maximum acceleration response and test speed

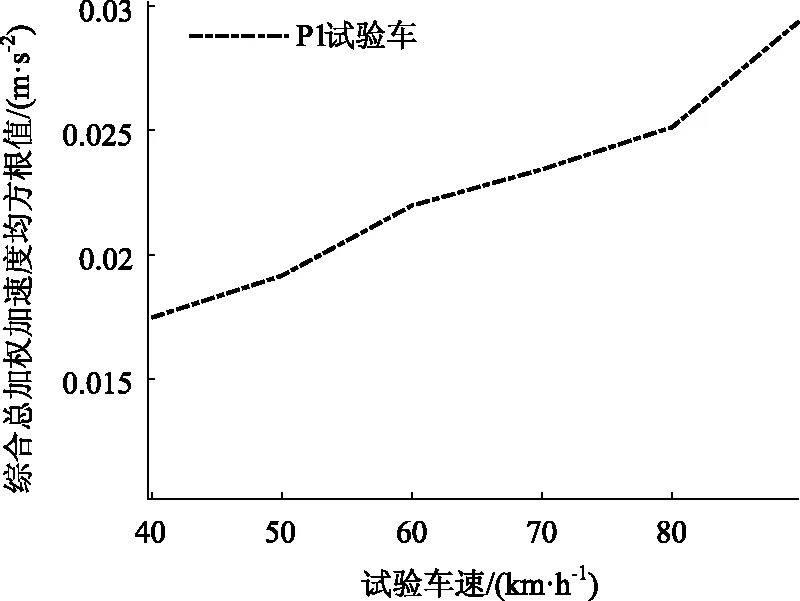
图2 综合总加权加速度均方根值与试验车速的关系Fig.2 Relationship between rms of integrated total weighted acceleration and test speed

3 振动舒适性主、客观评价模型

若全面考虑脉冲试验和随机试验各车速下的客观测量数据，则数据集过于庞大，且每个车速对主观评价的影响因子大小不能确定，不利于评价模型的建立。故本次研究中，基于驾驶人的实际道路驾驶经验，选择脉冲输入试验车速20 km/h和随机输入试验车速60 km/h作为评价车速，测量数据见表6。

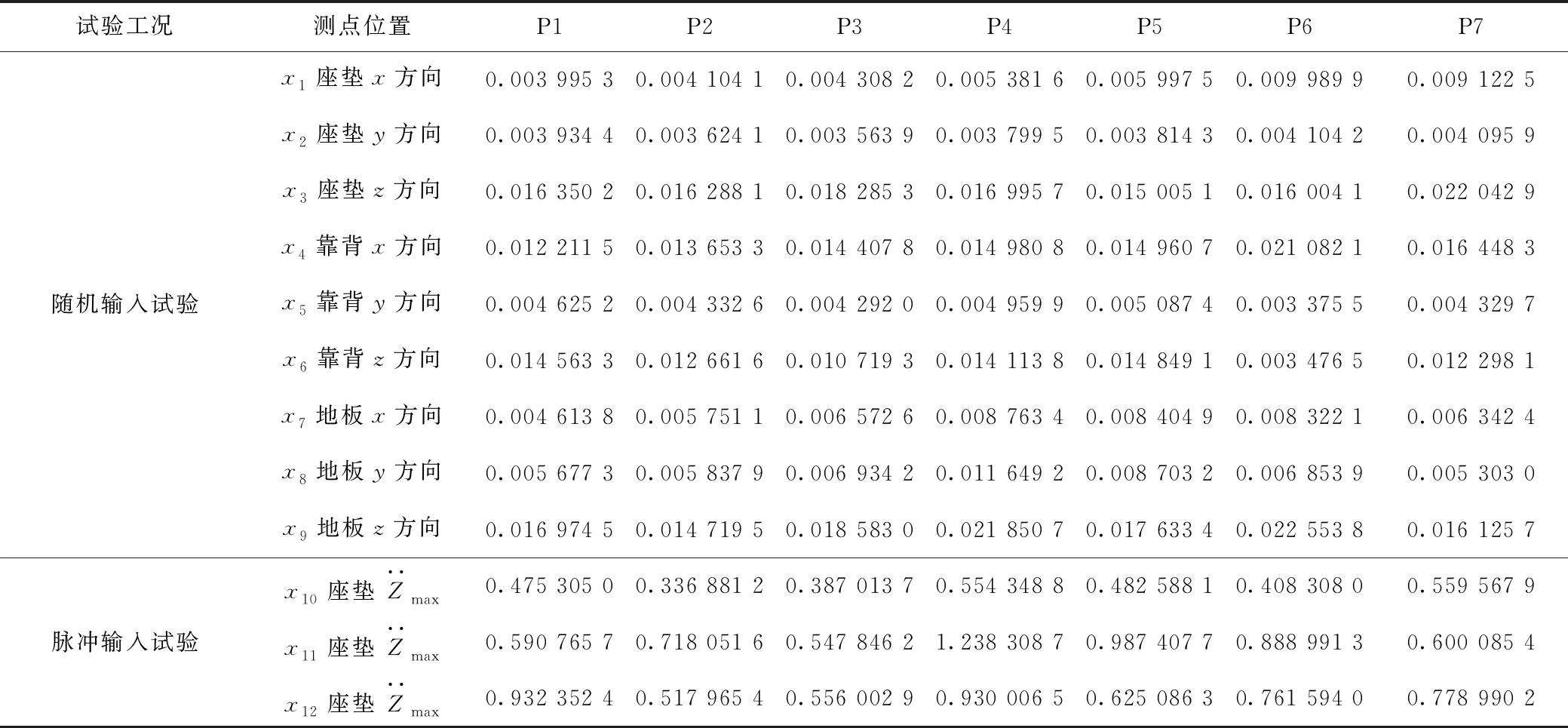
表6 各试验车测点及测量数据

3.1 客观数据关联度分析

灰色关联度分析(grey relation analysis, GRA)是一种定量描述变量之间关联程度的分析方法，且适用于小样本、无规律性数据[16]。本研究选用GRA定量分析12个客观指标对舒适性主观评价结果的影响程度，找到影响舒适性得分的主要因素，用于主、客观评价模型的建立。其中，主观评价得分x0(k)(k=1, 2,…,m)为参考数列，客观测量数据xi(k)(i=1,2,…,n)为比较数列。

3.1.1 数据预处理

进行关联度计算之前，采用均值化对数据进行无量纲化预处理，避免数据的量纲和数值差异对分析结果带来影响。

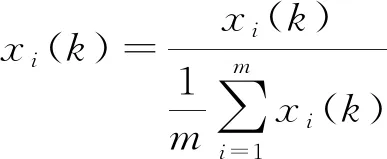
(i=0, 1,…,n，k=1, 2,…,m),

(1)

3.1.2 关联系数计算

计算差序列|x0(k)-xi(k)|并找出最大值M和最小值m。计算k时刻比较数列和参考数列x0(k)的关联系数ξ0i(k)：

ξ0i(k)=

(2)

式中ρ为分辨系数，ρ∈[0,1], 本研究取ρ=0.5。

3.1.3 关联度计算、

计算两个数列关联系数的平均值，得到关联度：

(3)

结果见表7。

表7 各因素的关联度

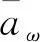
3.2 支持向量机模型

支持向量机(support vector machine, SVM)适用于小样本、非线性问题[17]，它首先对输入向量做升维处理，再利用核函数将其映射到高维空间，在这个空间对数据进行拟合处理。试验车样本为小样本，且待预测的主观评价分值与客观测量参数之间不呈线性相关，故建立支持向量机预测模型。

将GRA筛选后的客观测量数据作为输入变量，主观得分作为输出变量，建立基于实车试验的乘用车振动舒适性主观评价得分预测模型。

(1)将试验数据归一化处理。

(2)利用K-fold Cross Validation(K-CV)交叉验证模型经粗略选择和精细选择后，确定最优惩罚参数c=4和核函数参数g=0.062 5，结果见图3。

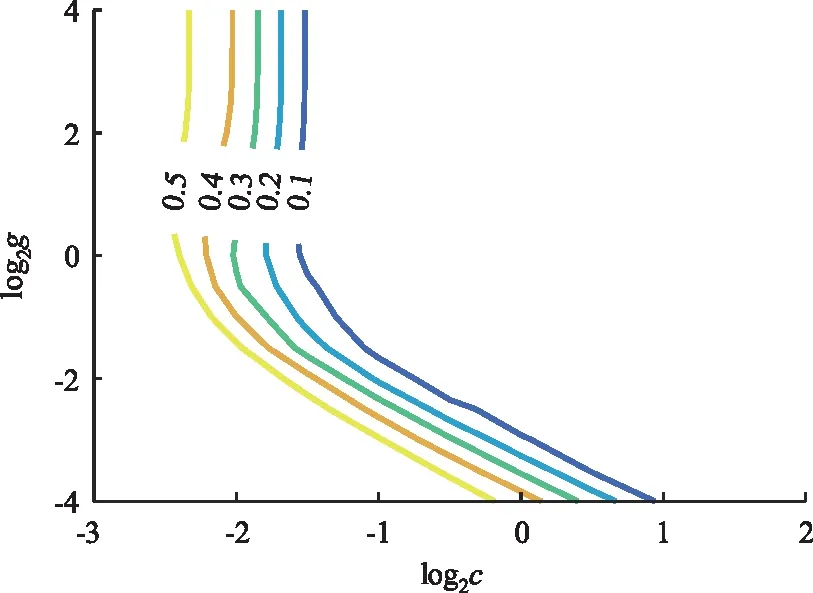
图3 精细选择图Fig.3 Fine selection graph

(3)利用最优参数对SVR模型进行训练，并预测振动舒适性主观评价得分，结果见图4。

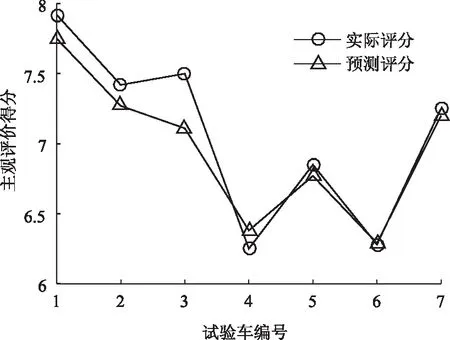
图4 SVM模型预测结果Fig.4 Prediction result of SVM model

3.3 BP神经网络模型

BP网络的特点是能够将误差反向传播来调整神经网络，直至输出期望值[18]。利用MATLAB建立包括输入层、隐含层、输出层的3层BP神经网络模型[19]并进行训练，输入参数为客观影响因素，即(x2,x3,x4,x5,x6,x7,x8,x9,x10,x12)，输出参数为主观评分。参考经验公式并经过多次试验确定隐含层节点数为7，即构建的神经网络结构为10-8-1。设置正切S形tansig函数和purelin函数为隐含层和输出层节点传递函数[20]。BP神经网络模型经过训练之后，对主观评分进行预测，见图5。

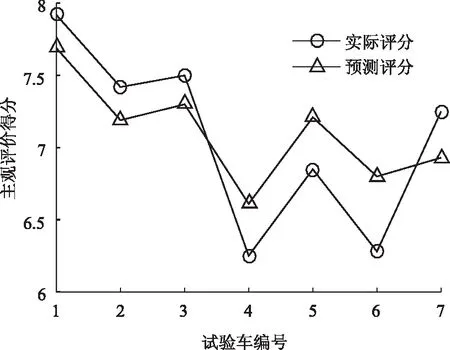
图5 BP神经网络模型预测结果Fig.5 Prediction result of BP neural network model

3.4 预测结果及模型对比

引入相对误差δ和均方根误差(RMSE)来分析SVM模型和BP神经网络模型的预测结果，比较2个模型的预测精度，实际评分与预测结果见表8。

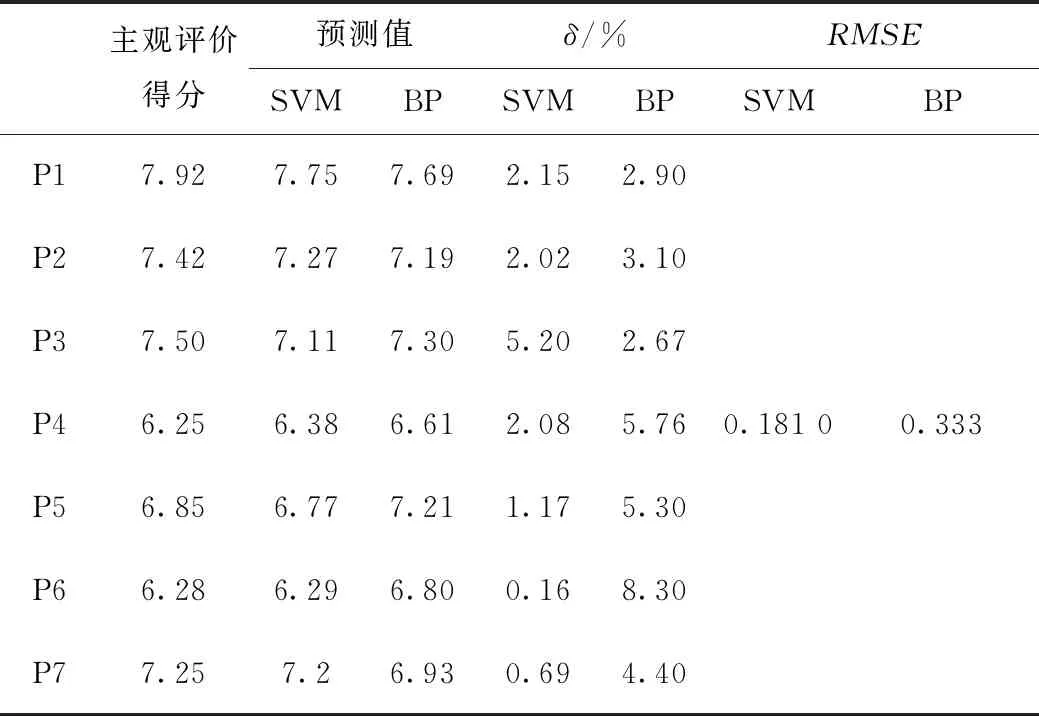
表8 实际评分与预测值对比

由比较结果可知，2种相关性模型对振动舒适性主观评价得分的预测误差均较小。SVM模型预测结果中，P3车辆预测相对误差较大，为5.02%，其余6辆车的预测相对误差都小于2.5%。BP神经网络模型由于训练样本数量少，预测误差偏大，P6车辆预测相对误差最大，为8.3%，其余6辆车预测相对误差在2.5%～5.8%之间。SVM模型预测结果的均方根误差也小于BP神经网络模型，因此SVM模型预测效果整体较好。

4 结论

为了实现乘用车振动舒适性主观评价客观化，选取7辆乘用车进行主、客观评价试验，获得主观评价指标得分和客观测量参数，并采用回归分析与BP神经网络建立了相关性模型。分析得到如下结论：

(1)脉冲输入试验中，当车速大于40 km/h时，最大加速度响应呈线性增长趋势变缓，即当车速大于40 km/h时，脉冲输入行驶中，车速变化对振动变化的影响减小。随机输入试验中，综合总加权加速度均方根值随车速呈线性增长趋势。

(3)经对比分析，支持向量机模型预测精确度更高，稳定性较好，更适合解决振动舒适性评价预测的小样本问题。