液压夯实机补强台背路基影响因素分析

姬 猛，徐天宇，陈策策，周志军,4

(1.中交二公局第四工程有限公司，河南 洛阳 471013；2.长安大学 公路学院，陕西 西安 710064；3.中国公路工程咨询集团有限公司，北京 100089；4.西安长大公路工程检测中心，陕西 西安 710064)

0 引言

桥台背路基的处理问题是国内外工程领域重要研究课题之一，强夯法对黄土地区台背路基补强效果显著[1-2]，但是已有研究表明，当夯点落在距台背2 m范围内时，强夯产生的巨大能量会以振动波的形式对桥台产生巨大的冲击作用，桥台结构物在冲击荷载作用下将产生沿路基纵向的动位移，并在桥台底部产生拉应变，当动位移或拉应变过大时，桥台将发生失稳破坏[3-4]。液压夯实机作为轻型强夯设备，可以对狭小区域进行作业，保证台背路基的压实质量[5-6]，但冲击振动作用仍会对桥台产生影响。

考虑冲击振动作用对既有结构物的影响，李廷、孔令伟等学者基于强夯法对边界接触应力和沉降特性进行了理论研究[7]，张涛为了研究强夯振动对周边环境的影响，对某强夯处理过程的振动进行了监测，发现强夯对建筑物产生了较大的动力影响，提出通过开挖减振沟减少强夯振动对建筑物的影响[8]，杨建国等人结合弹塑性有限元分析法，考虑对既有结构物的影响，分析了包括锤重和夯锤落距在内的强夯法加固设计参数[9]。在此基础上，冯雄辉开展了液压夯实法处理台背路基的现场试验，通过对比不同工况下的夯实效果，得出应力从夯点向下传播过程中存在一定的扩散角，水平向影响深度为1.5 m，提出夯点位置离桥台距离应大于1.5 m[10]。刘建奇等通过在涵洞背侧埋设位移传感器，采用位移指标评价夯击过程中夯击次数以及夯击点与结构物的水平距离对涵洞安全性的影响[11]，但没有对路基和涵洞本身的影响因素进行探讨。综上，目前的研究结果主要考虑夯击作用的水平影响范围，大都探讨夯击设备作业参数对结构物的影响，缺乏从路基、结构物和夯击设备三方面出发，综合探讨减弱对结构物动力影响的方法。

在液压夯实法补强路基过程中，桥台在夯击作用下的变形评价指标主要有台身裂缝宽度、桥台顶水平位移以及桥台的竖向沉降等[12-15]。由于桥台的竖向沉降通常不会超过规范允许值，因此现有模型通常用前两项指标来评价桥台的变形，而台身裂缝宽度和桥台顶水平位移可以通过监测台身最不利荷载作用位置桥台的动应变和顶端动位移来控制[16-19]。

因此，本研究采用ABAQUS有限元模拟液压夯实机补强台背路基的过程，建立“夯锤-路基-桥台”的相互作用模型，模拟夯点与桥台距离、路基初始压实度、桥台混凝土强度等级以及桥台顶部支撑条件对桥台变形的影响，通过对比不同工况下桥台的最大动位移及动应变值，分析夯击作用影响桥台变形的主要因素，为液压夯实机补强台背路基提供最佳施工参数。

1 工程概况

本研究依托某双向四车道高速公路路基填筑工程，设计速度80 km/h，路基宽度25.5 m，桥台长12.75 m，耳墙宽0.5 m，台高2.78 m。某标段共有台背路基12处，其中5处高度在2.56～3.06 m之间。为减少路基与桥梁结合部的差异沉降，避免桥头跳车，路堤与桥台、通道和涵洞连接处均设过渡段，过渡段路堤采用低液限粉质黄土填筑。本研究旨在通过室内足尺试验和有限元模拟结合，考虑液压夯实对桥台的动力影响，从定性和定量两方面分析得出本标段台背路基补强的最佳施工参数。通过室内土工试验得到表1所示的现场填土基本物理性质指标，这为建立有限元模型提供了材料参数。

表1 现场填料基本物理性质指标

2 数值模型建立

2.1 模型设计

为模拟路基施工现场液压夯实机补强桥台背路基，采用ABAQUS有限元软件，模拟HHT-66型液压夯实功能，桥台为钢筋混凝土结构，路基填料为黄土，路基每30 cm一层，共填筑8层，考虑路基填筑高度的足尺性，模型路基尺寸为8 m×6 m×2.5 m，压路机初步碾压后的压实度为85%，台背路基补强的仿真模型如图1(b)所示。

2.2 材料参数

路基填料为黄土，桥台属于轻型钢筋混凝土结构，夯锤材料为钢，各材料尺寸及材料参数见表2。

表2 仿真模型各部件尺寸及材料参数

2.3 创建部件与约束设置

创建液压夯锤、桥台、路基3个部件，由于主要研究桥台在液压夯实机补强黄土路基过程中的动态响应，可以不考虑夯锤的变形，故将其约束成刚体。在进行接触分析时，夯锤下表面为主面1，路基上表面为对应的从面1，路基与桥台接触的一侧为主面2，桥台与路基接触的一侧为对应的从面2，从而建立夯锤-路基、路基-桥台两组接触关系，接触属性选用库伦摩擦接触，切向作用采用“罚”函数算法，通过设置不同的摩擦系数对不同接触面间的摩擦行为进行模拟，法向作用则选取“硬接触”方式进行分析。根据相关资料文献[13,18-19]，夯锤与路基接触面的摩擦系数采用tan(0.5φ)=0.26, 路基与桥台接触面的摩擦系数采用tan(0.5φ)=0.39。

如图1所示，进行模型的边界条件设置时，将桥台底面、路基底面、路基与桥台未接触的面均设置为完全固结，约束桥台侧面沿路基横断面方向、竖直方向的位移和转动，仅保留桥台沿路基纵向的位移和转动。现场试验中，桥台两侧有耳墙分布，耳墙的存在会约束土体的侧向变形，减小桥台的侧向位移，因此，数值模拟过程中将两侧路基土的位移和转角进行了约束，故图1模型中将两侧耳墙去除。

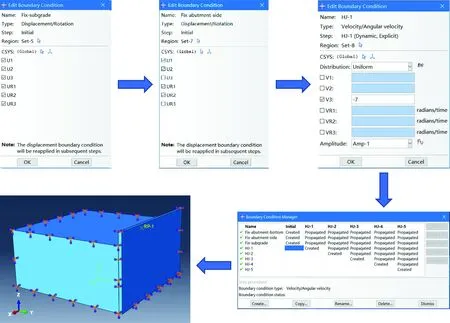
图1 模型施加边界条件Fig.1 Boundary conditions imposed on model

采用对夯锤施加竖直方向的速度为边界条件，以模拟夯击过程，夯锤落距2.2 m，落地速度为7 m/s。

2.4 单元类型

路基和桥台均采用三维实体，在划分网格时，均选用八节点六面体减缩积分(C3D8R)实体单元进行划分。为了尽可能接近实际工作性状，在划分网格时，将夯锤-路基接触位置处1 m×1 m范围内的网格进行加密划分。对本研究重点研究的桥台网格适当缩小，而在非加密区网格尺寸相对较大，使整个模型达到疏密结合的效果，从而保证模型能够更快更准确地收敛。网格划分完成的模型如图2(a)所示。

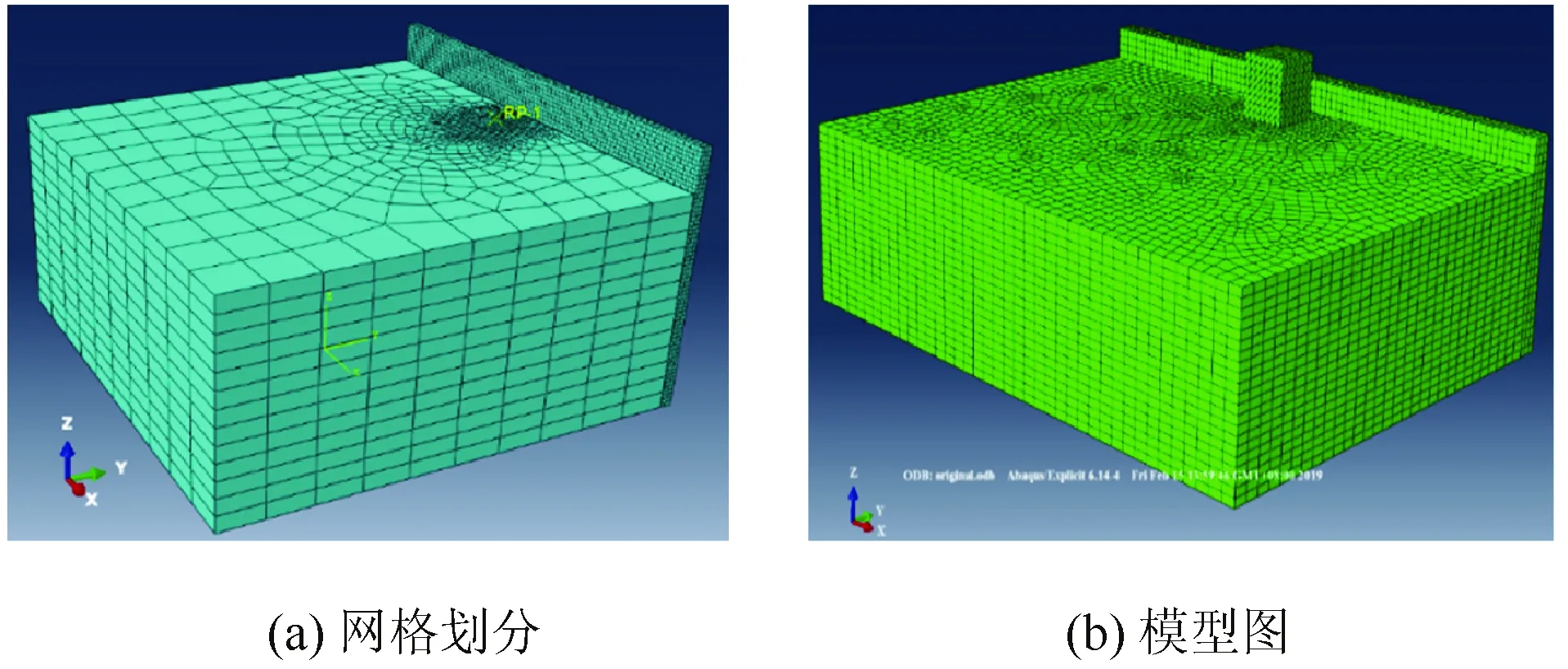
图2 路基补强模型Fig.2 Subgrade reinforcement model

至此，建模过程结束，经过数据提交与运算后便可进行后处理。

3 数值模型验证

3.1 室内试验设计

为验证模型的准确性，开展了液压夯实机夯击桥台背路基的足尺试验，夯锤落距2.2 m，夯点边缘距桥台60 cm，液压夯实机采用HHT-66型。由于夯击过程中，试验场地现存的位置固定且将通道墙作为模型“桥台”，刚度较大，钢筋混凝土动应变和桥台顶端动位移数据很难测得，考虑混凝土动应变和桥台顶端动位移主要由振动冲击作用导致，此过程中土体会挤压台背，台背会受动态土压力的作用，而动态土压力数据容易准确采集，故先将足尺试验采集的动态土压力数据和有限元仿真模拟的动态土压力数据作对比，验证模型的准确性。

试验中共埋设4个应变式土压力盒，分2层布设，为避免传感器超量程工作，拟定的测点埋置深度分别为60 cm和120 cm，土压力固定于桥台背表面，受力面沿桥台竖直方向，用于测量夯击过程中对桥台的的动态土压力值，采集设备采用DH5922系统，试验布置方案与试验过程如图3所示。

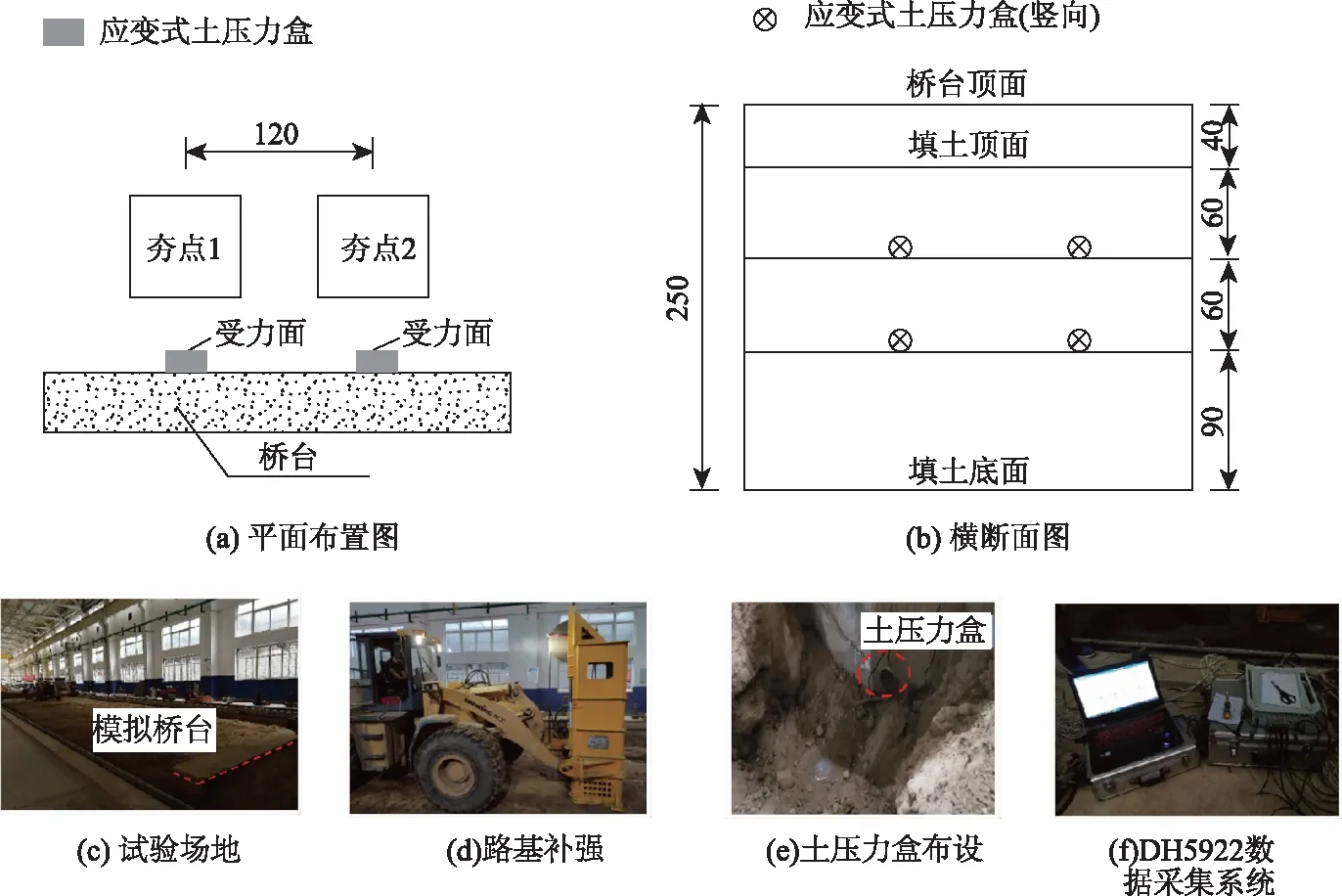
图3 台背土压力试验(单位：cm)Fig.3 Earth pressure test on abutment back(unit：cm)

3.2 土压力对比分析

图4为仿真模拟过程中夯锤下方60 cm深度处动态土压力随夯击次数的变化曲线，曲线中的5个峰值为5次夯击作用下的动态土压力峰值。通过提取5个峰值可以得到60 cm深度处的动态土压力峰值，同理可得120 cm深度处的动态土压力峰值，如表3所示。

图4 60 cm深度处动态土压力变化情况Fig.4 Change of dynamic earth pressure at 60 cm depth

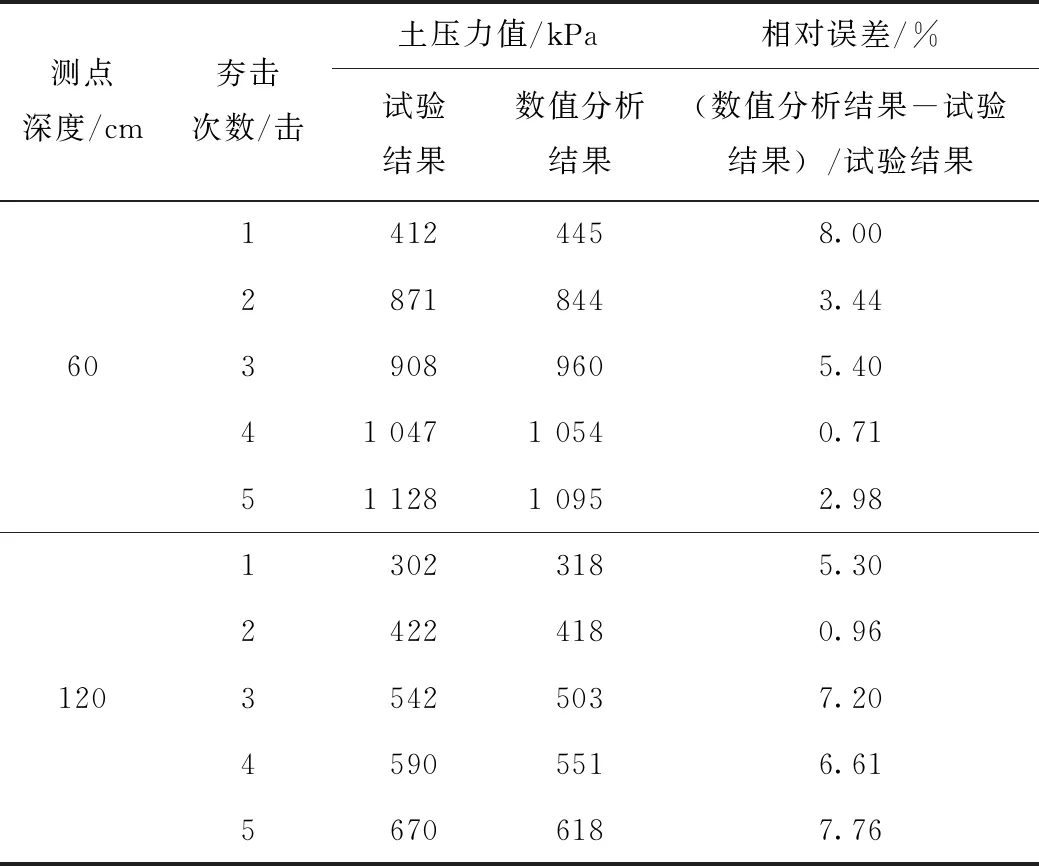
表3 足尺试验与有限元模型动态土压力结果

在同一坐标系中将仿真模型中60和120 cm深度处动态土压力峰值的变化情况与模型试验中的数据进行绘制，如图5所示。由图5和表3可知：对于动态土压力的计算结果，仿真模型的模拟值与试验的实测值变化规律一致，数值误差均小于10%，说明仿真模型的计算结果准确可靠，模型可行。

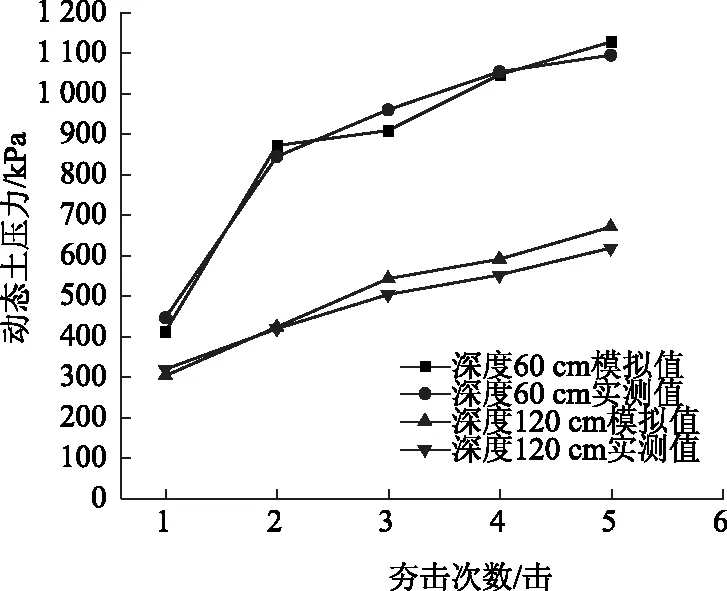
图5 不同深度处动态土压力变化情况Fig.5 Changes of dynamic earth pressure at different depths

3.3 数值模型动位移结果

由图6仿真模型的动位移云图可知，夯击过程中桥台动位移最大的位置为桥台顶端中心位置，最大动位移为2.73 mm，远远小于规范提出的桥台最大动位移2.5 cm的限值[17]，因此桥台在夯击作用下的动位移符合规范要求，该工况下的桥台处于稳定状态，从动位移沿桥台高度的分布可知，由于桥台底部为三向约束的固定端，桥台在夯击作用下的变形与悬臂梁受荷载作用的变形相同，桥台动位移沿桥台入土深度的增加而减小,残余位移也呈同样的规律变化，与理论情况相符，模型可行。

图6 仿真模型动位移变化Fig.6 Changes of dynamic displacement in simulation model

3.4 数值模型动应变结果

由图7仿真模型中桥台的动应变云图可知，仿真模型的最大拉应变为70 με，尚未达到150 με的混凝土开裂允许应变[17]，因此本模型试验的桥台混凝土未产生裂缝，桥台在夯击作用下未发生破坏，由动应变沿桥台高度的变化曲线可知，上部桥台主要承受夯击作用产生的压应变，桥台下部因桥台动位移的作用而产生拉应变，与理论情况相符，模型可行。

图7 仿真模型动应变变化Fig.7 Changes of dynamic strain in simulation model

4 桥台变形影响因素分析

4.1 夯锤落距对桥台变形的影响

带有液压蓄能器的夯实机，在夯锤释放前可施加初始压力，以实现低落距高能量的效果。HHT-66型液压夯实机最高落距为2.2 m，对应夯击能为66 kJ，为了简化模型，可通过提高夯锤落距来等效模拟初始压力，夯锤下落仍可视为自由落体，故以2，4，6，8和10 m 共5种不同落距进行分析，研究夯击能对桥台变形的影响，不同落距对应夯锤的落地速度分别为6.26，8.85， 10.84，12.52和14.00 m/s。

图8所示为桥台最大动位移和动应变随夯锤落距的变化规律。由图8可知，相同落距下，随着夯击次数的增加，桥台最大动位移和最大动应变在某一区间内波动，在第2击结束时两者都出现最大值，考虑最不利状况，图9回归分析了第2击结束时桥台最大动位移及最大动应变与夯锤落距的关系，由图9可知：(1)在2～10 m落距范围内，桥台顶端的最大动位移smax随夯锤落距h增加呈线性增长，遵循smax=0.18h+2.38的规律。(2)最大动应变εmax随夯锤落距h增加呈线性增长，遵循εmax=7.3h+48.4的规律。

图8 桥台最大动位移及动应变随夯锤落距变化Fig.8 Maximum dynamic displacement and maximum dynamic strain of abutment varying with dropping distance of rammer

图9 桥台最大动位移及动应变与夯锤落距关系Fig.9 relationship between maximum dynamic displacement and maximum dynamic strain with dropping distance of rammer

4.2 夯点与桥台距离对桥台变形的影响

采用液压夯实法对桥台背路基进行夯击补强时，夯锤边缘与桥台距离的选择是控制实际夯击位置的重要参数。本研究采用自重3 t，底面面积为0.7 m×0.7 m的夯锤，通过调整夯锤位置，实现落距2.2 m时夯锤边缘距桥台10，20，30，40，50 cm共5种不同工况，进而研究夯锤与桥台不同间距情况下桥台的动力响应，如图10所示。

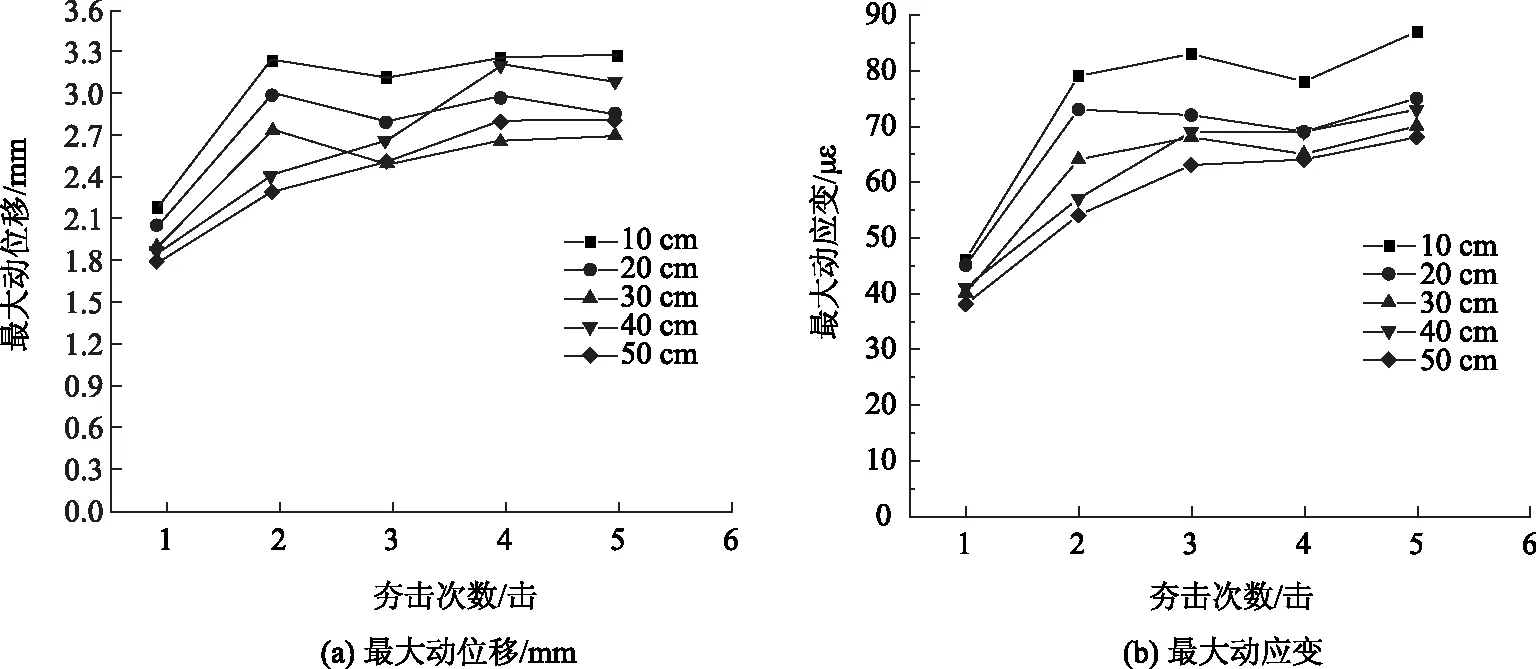
图10 桥台最大动位移及动应变随夯点与桥台距离变化Fig.10 Maximum dynamic displacement and maximum dynamic strain of abutment varying with distance between compacting point and abutment

图11所示为桥台最大动位移和动应变随夯锤边缘与桥台距离的变化规律。由图可知：(1)桥台顶端最大动位移随着夯锤与桥台距离的增加而逐渐减小，二者之间呈负线性相关，最大动位移smax与夯锤边缘距桥台的距离d之间遵循smax=-2.49d+3.47的变化规律。(2)桥台动应变εmax的变化规律与桥台顶端最大动位移的变化规律基本一致，与夯锤距桥台距离之间也呈负线性相关，遵循εmax=-66.00d+85.20的变化规律。

图11 桥台最大动位移及动应变随夯锤边缘与桥台距离关系Fig.11 Relationships of maximum dynamic displacement and maximum dynamic strain of abutment with distance between rammer edge and abutment

4.3 路基初始压实度对桥台变形的影响

本研究足尺试验采用的路基填土最大干密度为1.900 g/cm3，最佳含水率为12.3%，100%压实度对应的路基填土密度为2.134 g/cm3。通过对模型参数中路基土密度的修改，实现路基压实度分别为75%，80%，85%，90%和95%共5种不同的工况，各工况对应的路基填土密度分别为1.600，1.707，1.814，1.921，2.027 g/cm3。

根据图12桥台最大动位移及动应变随路基压实度的变化图可知：在路基压实度由75%增加至95%的过程中，桥台最大动位移曲线基本呈重合状态，动位移随压实度变化不明显。桥台动应变的变化规律与动位移的变化规律基本一致，最大动应变波动不超过5 με，说明在不同路基压实度工况下夯击作用对桥台的影响效应不明显。

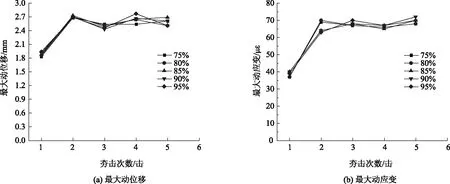
图12 桥台最大动位移及动应变随路基压实度变化Fig.12 Maximum dynamic displacement and maximum dynamic strain of abutment varying with compaction degree of subgrade

4.4 桥台混凝土强度等级对桥台变形的影响

随着桥台混凝土强度等级的提高，混凝土的弹性模量Ec也随之增长，进而导致桥台的抗弯刚度EI一并提高，由混凝土的本构关系可知，桥台动应变将按负幂指数形式变化[20-21]，本研究将对此结论进行验证并分析桥台动位移的变化规律,所选择的混凝土强度等级分别为C20，C25，C30和C35。

由图13可知：(1)桥台最大动位移与动应变的变化规律基本一致，混凝土强度等级越低，夯击作用下桥台的最大动位移和动应变越大。桥台采用C20

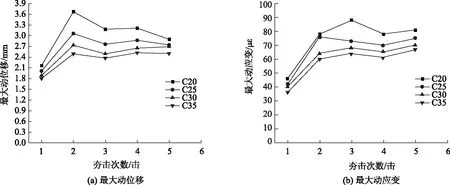
图13 桥台最大动位移及动应变随混凝土强度变化Fig.13 Maximum dynamic displacement and maximum dynamic strain of abutment varying with concrete strength

混凝土时，其最大动位移为3.67 mm，最大动应变为88 με，均符合规范要求[17]。(2)随着混凝土强度等级的提高，桥台最大动位移及桥台动应变均有所减小。图14中分别采用负幂指数函数和一次函数对桥台第2击结束时的最大动位移smax与混凝土强度等级C的关系进行拟合，结果表明当采用smax=29.9×C-0.7拟合时，拟合度达到0.99，而采用smax=0.07C+5.12拟合时,拟合度仅为0.93，说明最大动位移与混凝土强度等级之间更满足负幂指数函数关系。

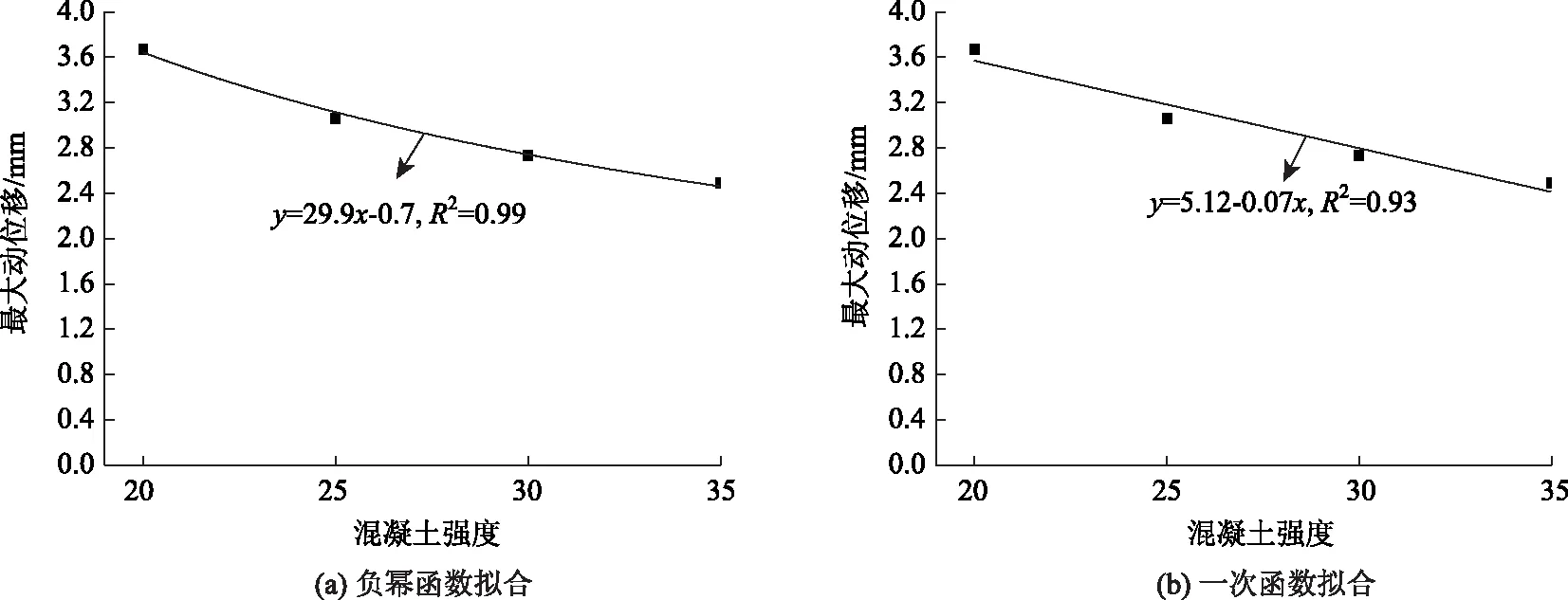
图14 桥台最大动位移与混凝土强度的关系Fig.14 Relationship between maximum dynamic displacement of abutment and strength of concrete

4.5 桥台顶部支撑条件对桥台变形的影响

由图15(a)所示的桥台受力及支座条件简化图可知：当对桥台背路基进行夯击补强处理时，桥台顶部的支撑条件对其变形将产生显著的影响，即当桥台顶部台帽处由桥面板完全支撑，无伸缩缝时，在夯击振动力作用下，台顶的水平位移将会很小，台身的弯曲变形也较小，其承受振动冲击的能力将较大。当台顶的台帽与桥面板间留有一定的伸缩缝时，在夯击作用下，台顶的水平位移较大，桥台的受力状态与悬臂梁相似，台身在地基支撑梁处产生较大的弯拉应变，当土质地基不是很坚硬时，将会产生绕地基支撑梁转动的可能。下面将伸缩缝对夯击结果的影响进行量化：由图15(b)～(c)有限元模拟结果可知，当桥台顶部无伸缩缝时，桥台在夯击作用下的最大动位移位置位于桥台中部，其变形与有伸缩缝时明显不同。由图16可知，无伸缩缝时的桥台位移随台高呈先增大后减小的趋势，类似于简支梁受集中荷载的情况，而有伸缩缝时的桥台位移随台高变形图更接近悬臂梁的情况。

图15 桥台支撑条件及最大动位移云图(单位：mm)Fig.15 Nephograms of abutment support condition and maximum dynamic displacement(unit：mm)

图16 不同顶部支撑条件下动位移随桥台高度变化Fig.16 Dynamic displacement varying with abutment height under different top support conditions

图17所示为桥台最大动位移及动应变随夯击次数的变化情况，无伸缩缝工况下桥台的最大动位移及动应变均明显小于有伸缩缝工况。随着夯击次数的增加，无伸缩缝情况下桥台的位移及应变在第二次夯击之后便趋于稳定。此次夯击过程中，桥台最大动位移在有无伸缩缝两种工况下分别为0.68和2.69 mm，无伸缩缝时最大动位移减小了75%。桥台最大动应变在有无伸缩缝两种工况下分别为70和53 με，无伸缩缝时的最大动应变减小了24%，说明无伸缩缝时桥台承受振动冲击的能力显著增强。

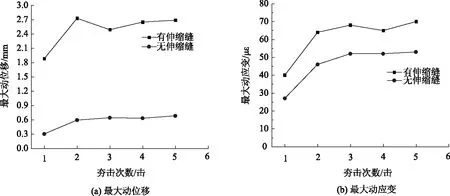
图17 不同顶部支撑条件下桥台最大动位移和动应变Fig.17 Maximum dynamic displacement and maximum dynamic strain of abutment under different top support conditions

5 结论

本研究依托某高速公路桥隧过渡段台背路基填筑工程，首先采用ABAQUS建立液压夯实机补强台背路基模型，结合既有试验数据和研究成果对模型进行了验证。进一步研究夯锤落距、夯点与桥台距离、路基初始压实度、桥台混凝土强度等级和桥台顶部支撑条件对桥台变形的的影响，得出结论如下：

(1)采用仿真模型对液压夯实法补强台背路基过程中台背土压力进行分析，其结果与室内足尺试验误差基本在10%以内，桥台动位移和动应变沿桥台高度方向的变化趋势与既有研究成果一致，有限元模拟能够较准确反映工程实际情况。

(2)桥台在夯击作用下的最大动位移及最大动应变随夯锤落距的增加呈线性增大，随夯点与桥台间距离的减小呈指数型增大。路基初始压实度由75%增加至95%过程中，桥台最大动位移变化趋势基本一致，最大动应变波动不超过5 με，路基初始压实度的变化对桥台变形影响较小。

(3)桥台混凝土强度等级提高，其最大动位移及动应变相应减小。当桥台顶部无伸缩缝时，最大动位移和最大动应变相比于有伸缩缝时分别减小了75%和24%，说明无伸缩缝时桥台承受冲击荷载的能力显著增强，补强过程中可采用临时阻塞桥梁伸缩缝的方法改变桥台的受力形式。

(4)研究成果为台背路基补强施工时桥台的变形分析提供了思路，对提高施工过程中桥台的安全性具有指导意义。但是，实际桥台往往有耳墙的存在，耳墙与边坡的自由边界是非完全约束的，受室内模型试验条件的限制，本研究中试验槽两侧是完全约束的，这会增强夯锤夯击过程中对桥台的动力影响，因此，后期开展现场试验过程中需进一步分析约束条件带来的误差。