钢-混连续组合梁的徐变等温法

陈 旭，章胜平，王春华，宋高丽，潘维平

(1.昆明学院 建筑工程学院，云南 昆明 650214;2.昆明理工大学 建筑工程学院，云南 昆明 650504)

0 引言

钢-混组合梁充分发挥了型钢与混凝土材料性能优势，具有强度高、刚度大、延性好等优点。然而连续组合梁负弯矩区组合截面处于力学劣势(混凝土板受拉，型钢受压)，使混凝土桥面板在使用中受拉开裂，产生钢筋锈蚀等耐久性问题，严重影响了桥梁结构工作性能和使用寿命。连续组合梁钢截面和负弯矩区混凝土开裂不考虑徐变，混凝土正弯矩区考虑徐变，意味着正弯矩区刚度随着时间逐渐地相对减少，负弯矩区刚度相对地增加，由此带来不利的冗余支座次弯矩增加，徐变次弯矩将加重钢梁应力风险。另外，大跨度组合梁长期下挠增加，严重影响了对挠度要求严格的高速铁路等结构的安全性。这些问题与混凝土徐变和收缩有关[1-5]。

徐变是混凝土在持续应力方向发生的，与时间相关的变形增加，等效于刚度的减小，如果用一个折减系数表示，将该折减系数乘以弹性模量，得到徐变换算模量[6-8]。基于徐变换算模量的有限元分析[9]是超静定结构分析的主要方法之一，文献[10]用ABAQUS软件对连续组合梁考虑开裂和徐变等进行了三维分析，文献[11]用MIDAS软件对连续组合梁考虑施工过程和徐变试验数据修正等徐变影响。解析法是有限元分析的有益补充[12]。与徐变换算模量比较，更为简单方便的是等温法[13]，因能更便洁地用于结构分析软件。

徐变等温法是将收缩徐变效应等效为温度梯度效应，如《钢结构设计标准》(GB50017—2017)有“混凝土收缩产生的内力及变形可按组合梁混凝土板与钢梁的温差-15 ℃计算”[14]。除了收缩引起的徐变效应，还有永久荷载、支座位移等其他荷载类型引起的徐变效应，而目前相关规范针对其他荷载类型作用没有给出相应的内容。为此，本研究采用解析法推导永久荷载作用组合梁徐变的等效温度梯度的计算公式。

1 规范理解与假定

现有规范徐变效应计算包括定值有效模量比、定值徐变因子[15]和降温3种简化方式。

1.1 定值有效模量比

在工程实践中通常将徐变效应以折减混凝土弹性模量方式简化计算。如《钢结构设计标准》[13]，有效模量比等于2。

(1)

式中，nφ为徐变后模量比;n0为徐变前模量比;Es为钢弹性模量;Ec0为徐变前混凝土弹性模量;Ect为徐变后混凝土弹性模量。

该模量比应用简单，但是没有考虑加载龄期等混凝土自身和外部环境因素影响。如，加载龄期早，徐变大，有效模量比大；室内环境相比室外干燥，相对湿度小，徐变大，有效模量比大。另外，也没有考虑荷载类型对徐变的影响。如，人们将连续梁内支点施加支座沉降(强迫位移)产生正弯矩以达到减小负弯矩的目的，效果却不佳，因为强迫位移这种荷载类型的徐变效应大，正弯矩因徐变而折减较多。因此徐变效应分析首先应区分荷载类型。

Bode对钢-混凝土组合梁给出了考虑加载龄期、环境相对湿度(室内、室外)和荷载类型(永久作用、收缩和强迫位移)定值有效模量比计算表[16](见表1)。

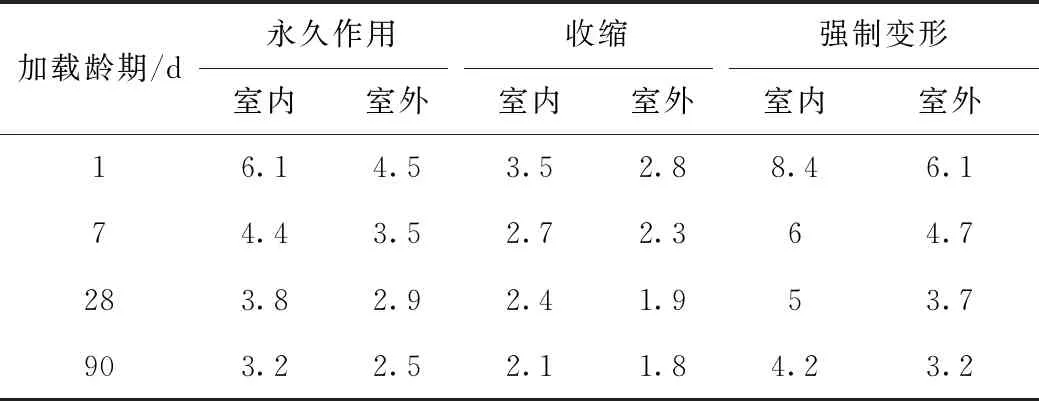
表1 有效模量比Tab.1 Effective module ratio

虽然表1定值有效模量比已是细致，但忽略了徐变系数与时间的发展关系。如，徐变与应力持续时间的关系；应力持续时间越长，徐变越大，有效模量比越大。因此，将有效模量比表示为徐变系数的函数，可实现定值有效模量比的改进，即为基于徐变因子的有效弹性模量法。

1.2 定值徐变因子

《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[17]参考欧洲规范4，按照应力产生的原因将荷载分为3种类型，给出了不同荷载类型的定值徐变因子(ψL)，即永久作用徐变因子1.1，用于调整内力的强迫位移作用徐变因子1.5，混凝土收缩作用徐变因子0.55。则徐变后混凝土弹性模量变为:

(2)

式中，φ(t,t0)为t时刻徐变系数;t0为加载龄期。

有效模量比为:

(3)

现行欧洲规范4徐变因子，由德国学者Roik及其学生提出，其推导过程与理解见文献[6]和文献[18]，其基本假定为：

(1)伯努利平截面假定；

(2)混凝土不开裂；

(3)钢和混凝土在瞬时荷载作用下满足胡克定律；

(4)在正常使用条件下，混凝土为线性黏弹性体，混凝土应力-应变关系满足Boltzmann叠加原理；

(5)收缩与徐变变化规律相同。

Roik按照弯曲、轴压、收缩和强迫位移作用4种荷载类型，通过截面分析推导获得相应的定值徐变因子，没有考虑钢梁与混凝土板交界面弹性连接产生的相对滑移，认为钢梁与混凝土板没有竖向分开，在二者的交界处，它们的竖向变形保持一致。换句话说，欧洲规范4定值徐变因子反映的是单独的徐变效应。Roik定值徐变因子依据德国旧规范DIN 4227徐变系数，出现了欧洲规范4徐变因子与欧洲规范2徐变系数不一致的情况，另外Roik定值徐变因子推导假定忽略混凝土板弯曲变形引起的轴向应变(不符合矮梁特性)，对此Kindmann等进行了改进并提出了一套新的定值徐变因子[19]。

1.3 降温法

《钢结构设计标准》[13]建议收缩作用徐变效应计算采用温差-15 ℃“定值降温”。降温法是将徐变等效为温度梯度作用(线性)。借鉴收缩作用“降温法”思路，本研究对永久作用等温法公式解析解进行了推导，推导遵循欧洲规范4徐变因子基本假定，因此本研究等效温度梯度解析解可与Kindmann徐变因子算例对比验证(见表2)。

虽然欧洲规范4定值徐变因子或等效温度梯度适用于静定梁，也适用于超静定梁，静定和超静定梁等效温度梯度公式(第2节)相同，但超静定梁弯曲刚度因负弯矩区纵向变化情况复杂。本研究等效温度梯度公式应用(第3节)选择超静定梁进行计算分析。超静定负弯矩区混凝土开裂后退出工作，组合截面变为钢截面(型钢+钢筋)，不考虑混凝土徐变，因此需要确定负弯矩区范围。采用数值迭代精确计算负弯矩区范围过程复杂，无法在简化计算中应用，因此本研究采用欧洲规范4假定，即负弯矩区为跨度的0.15倍，负弯矩区不考虑混凝土徐变。

这样，永久荷载作用超静定连续梁徐变等温法计算思路为：按照第2节解析解计算正弯矩区永久荷载作用等效温度梯度，则徐变后超静定连续梁的内力和变形转化为“按照材料和结构力学方法计算温度梯度作用超静定结构内力(截面重分布内力和超静定支座次内力)和变形”。

2 公式推导

2.1 等效温度梯度解析解

分析组合梁徐变与温度梯度作用，不难发现二者的相似之处：在正弯矩区，徐变使得混凝土板应力减小，钢截面应力增加，梁的曲率和变形增加，这相当于在截面高度方向施加了一个线性温度差，上边缘相对地降温，下边缘相对地升温。当截面高度为h，在组合梁高度方向作用线性分布温度梯度，当上、下边缘温度梯度为TΔ时，产生曲率(κT)为

(4)

式中，αT为混凝土或钢材的温度线膨胀系数(混凝土或钢材的温度线膨胀系数几乎相同[13])，通常取αT=1×10-5℃。

如果已知徐变引起的曲率，按照曲率等效原则，由式(4)计算将得到徐变所等效温度梯度(见图1)，将温度梯度施加于连续梁的正弯矩区，得到冗余支座温度梯度次弯矩就是徐变次弯矩。另外，由式(4)可知，线性温度梯度在数值上相当于截面的无量纲曲率(曲率与截面高度的乘积)，而曲率反映了截面的转角大小。换言之，在物理含义上，等效温度梯度还表示了组合梁徐变引起的截面相对转角大小。

图1 等效温度Fig.1 Equivalent temperature

由基本假定知组合梁曲率等于钢截面曲率，徐变引起的曲率变化(徐变曲率κcr)表示为:

(5)

式中，Msr为钢截面的重分布弯矩;Is为钢截面惯性矩。钢截面包括型钢、普通钢筋(或预应力钢筋)，在平截面假设条件下不同类型的钢材可换算为一个钢截面。

联立式(4)和式(5)，徐变等效温度梯度

(6)

Msr是组合截面在持续作用下徐变所引起的部分截面重分布内力之一(下标用r表示)。如图2所示，混凝土板(下标用c表示)和钢(下标用s表示)两个部分截面内力，按照时间分为t0的初始内力(Mc0，Nc0，Ms0和Ns0)、重分布内力(Mcr，Ncr，Msr和Nsr)、微分增量内力(dMcr，dNcr，dMsr和dNsr)。图2及文中失量的符号规定为：轴力或正应力以受拉为正以受压为负；弯矩或曲率以截面下边缘受拉为正，反之为负；剪力以使脱离体顺时针转动为正，反之为负。

图2 应变和内力Fig.2 Strains and internal forces

当考虑徐变时，截面刚度受到徐变的影响随时间而变化，刚度是未知量，如果采用位移法，不能直接由内力计算位移(应变和曲率)，需借助于数值迭代逐步计算，无法建立变量之间的解析关系。因此为获得重分布内力的解析解，采用力法建立以内力为未知量的在时间微分的变形(见图2)和平衡关系方程。当混凝土黏弹性本构选择改进迪辛格应力-徐变关系时，方程表示为:

(7)

式中，hd为板与钢梁重心轴之间的距离；Ac0和Ic0分别为混凝土面积Ac和惯性矩Ic按照弹性模量比n0的换算面积和惯性矩，Ac0=Ac/n0，Ic0=Ic/n0，n0=1.4Es/Ec，混凝土弹性模量Ec除以系数1.4是按照吕休的建议[20]，将徐变中滞后弹变剥离出来纳入初始弹性应变考虑，徐塑系数φt=[φ(t,t0)-0.4]/1.4，即徐塑系数是剥离徐变系数φ中的滞后弹性变形部分后所剩下的徐变塑性变形部分；徐变系数应该根据需要选择相应的规范计算或按照试验结果取值或修正。

当组合截面受到轴力(N0)和弯矩(M0)的压弯作用时，按照刚度的大小，混凝土板分配到的轴力(Nc0)和弯矩(Mc0)分别为:

(8)

式中，Ai为换算截面面积;Ii为换算截面惯性矩;Si为换算截面板或钢对重心轴的面积矩。

将式(7)整理得到以Msr为未知量的一元二阶微分方程

(9)

虽然式(9)在数学形式上是比较简洁的二阶常系数非齐次微分方程，但是它的手算求解过程还是比较复杂的，而且得出的解析解是非线性公式。尽管如此，解析解在其假设条件下为精确解，因此求出式(9)的解析解，联立式(8)，代入式(6)整理。按照叠加原理，将压弯截面分为纯压截面和纯弯截面，分别给出计算公式。

对纯压组合截面，等效温度梯度解析解为

(10)

对纯弯组合截面，等效温度梯度解析解为

(11)

从式(10)、(11)可知温度梯度与荷载线性相关，但还与其他许多参数和变量有关(如截面特性参数和徐变系数)，这些参量表达式复杂，难以分析出哪些是主要影响因子，为此开展简化分析工作。

2.2 等效温度梯度简化解析解

钢-混凝土组合截面弯曲刚度包括混凝土板、钢截面刚度和轴力组合刚度，通常轴力组合刚度占比大，板刚度占比小，因此按照刚度分配原则板重分布弯矩增量dMcr相比于组合轴力之矩hddNcr较小，在同一等式中忽略前者可以说是一个合理的简化。这样二阶的微分方程式(9)降阶为了一阶，即

(12)

求解式(12)：

Msr=(Mc0-hdNc0)(1-e-αsφt)。

(13)

这样对纯压组合截面，等效温度梯度公式简化为

(14)

对纯弯组合截面，等效温度梯度公式简化为

(15)

通过简化分析可知，约束系数αs是影响徐变效应的主要截面特性参数。αs反映了钢截面对混凝土板弯曲徐变的约束能力，钢截面对板的约束为偏心弹性约束，αs的取值介于0至1之间。

需要说明的是，等效温度梯度解析解与时间具有相关性(因为公式变量包括徐变系数)。当计算时间为某个特定时间(如10年)，徐变系数为定值，等效温度梯度为定值。这样，将定值等效温度梯度应用于有限元分析，相当于将徐变的非线性有限元分析转化为弹性有限元分析。

3 超静定连续梁计算分析

3.1 组合梁特性

选择文献[19]连续梁的计算数据，已知，

Es=2.1×105N/mm2，Ec=3.35×104N/mm2，

Ac=3×107mm2，Ic=5.625×108mm4，

As=1.89×104mm2，Is=6.416×108mm4，

h=540 mm，hd=227 mm，φ(t,t0)=2.5。

在均布荷载作用下，中间15%跨度范围的混凝土开裂(状态Ⅱ)，混凝土退出工作，混凝土板开裂之后不考虑徐变，截面为板内钢筋与钢梁组合的钢截面。按照阶跃式变刚度模型计算，内支座负弯矩为384.87 kN·m，跨内最大正弯矩为326.08 kN·m，见图3。

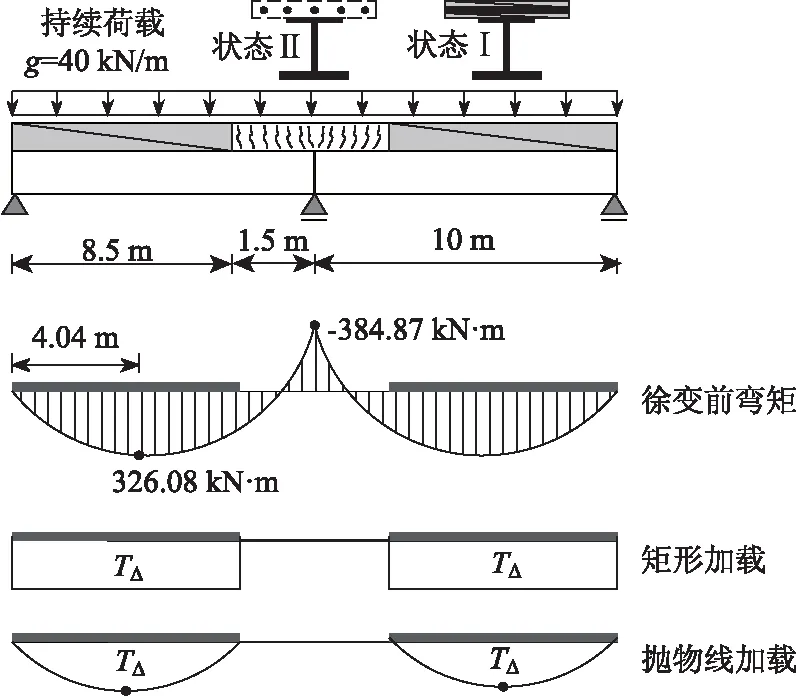
图3 计算简图Fig.3 Calculation diagram

3.2 温度梯度计算

正弯矩区的弯矩在长度方向为变量，计算最不利的最大正弯矩所等效的温度梯度，用到的参数有

Ec0=2.39×104N/mm2，n0=8.78，

Ac0=3.418×104mm2，Ic0=0.640 9×108mm4，

Ai=5.308×104mm2，Ii=13.328×108mm4，

jc=0.031，js=0.171，r1=-0.178，r2=-0.962，

αs=0.177，φt=1.5。

按照式(10)、式(11)的解析解有

0.249=16.9 ℃。

按照式(14)、(15)的简化解析解有

1-e-0.177×1.5=0.233，

0.233=15.8 ℃。

等效温度梯度的简化解析解与解析解的偏差为-6.5%，表明简化分析较大幅度地简化了公式，还具有较高的精度。

3.3 徐变效应计算

计算温度梯度产生的次弯矩，应该按照式(10)、(11)或式(14)、(15)计算正弯矩区每一截面弯矩所对应的温度差，由式(4)计算每一截面的曲率，再由虚功原理计算温度梯度在单位虚荷载方向的位移，这种精确计算方式在实践应用中有所不便。

简单方便也是比较常用的方法是：假设温度梯度在正弯矩区内为常量(按照最大正弯矩控制截面计算)，温度梯度均匀分布于正弯矩区，即矩形加载方式(见图3)。但是矩形加载方式是保守估计，计算结果偏差大，如表1矩形加载算得的徐变次弯矩69.08与文献[19]的45.1偏差为53%。

为此开展了一些比较分析工作，发现用抛物线加载方式计算方便，精度较好，如表2抛物线加载徐变次弯矩46.05与文献[19]的偏差2%。

从表2可见，负弯矩区混凝土板开裂之后，在挠度和内支座剪力增加不大的情况下(挠度增幅约11.5%，剪力增幅约8%)，出现了正弯矩增加(增幅约16%)和负弯矩减小(减幅约23%)的可喜现象。但随着时间发展，徐变产生了约58.6%的挠度增加，以及约12%的额外负弯矩，另一方面略缓解了内支座的剪力(减幅约4%)。由此可见，徐变效应与开裂效应作用相反，因为徐变退化了混凝土板的弯曲刚度。徐变对开裂效应的缓解作用还可从应力方面来反映。

表2 内力和挠度Tab. 2 Internal forces and deflections

承受动力荷载的组合桥梁等结构强度通常采用容许应力弹性设计法。连续梁冗余支座为不利截面，因为混凝土板受拉钢梁受压，与它们力学特性相反。计算冗余支座截面的正应力(见表3)，结果表明开裂之后截面应力得到较大幅度的释放。但是另一方面徐变又使得应力增加，其中钢梁下边缘的压应力增加较大(增幅约12%)。

表3 截面的正应力Tab.3 Normal stresses of cross-section

值得注意的是，对允许开裂的非预应力组合梁，如有较多应用的高配筋现浇混凝土连续组合梁[21]，须考虑徐变对开裂效应的缓解作用和对挠度的显著增加作用，作用程度的大小还与型钢大小等因素有关。

4 型钢大小影响

在工程实践中，钢-混组合截面特性在不同结构类型中特性差异较大，如在民用建筑中型钢尺寸小，在公路和铁路桥梁中型钢尺寸大，型钢大小是影响徐变的关键因素[15]。

选择变化3.1节组合梁特性中的钢梁大小，分析等效温度梯度的解析解和简化解之间的偏差，分析跨中挠度和徐变次弯矩等的变化范围(见图4)，其中型钢选择欧规HEA300至HEA1000的14个截面特性。

图4 型钢大小的影响Fig.4 Influence of size of section steel

从图4(a)型钢高度(等于牌号减去10 mm)曲线可见，约束系数与型钢高度具有正相关关系。从图4(b)和(c)可以看出，简化解式(10)～(13)能够较好地反映徐变的时随规律，能够作为解析解的有益补充。徐变导致的跨中挠度增加显著，在型钢牌号小的情况尤其应该重视(如在图4(d)中HEA300型钢徐变挠度增幅为73.5%)。在约束系数大的情况下(型钢牌号大)，徐变等效温度梯度可低于10 ℃。而在约束系数小的情况下，徐变等效温度梯度较大(超过30 ℃)，钢梁底部压应力较大(约150 MPa)，若再叠加其他作用引起的不利压应力，则钢梁底部很可能产生失稳破坏。

5 结论

等温法能够便洁地用于连续组合梁的长期力学分析。组合梁弯曲徐变与许多因素有关，如荷载类型、截面特性和组合梁特性，因此采用解析方法推导得到了永久荷载作用徐变等效温度梯度的解析解。

为进一步获知关键的主要影响因素，推导了解析解的简化解析解。研究表明对永久荷载作用下的钢-混连续组合梁，采用抛物线加载方式将等效温度作用于正弯矩区，徐变效应计算结果精度较高。徐变等温法为连续组合梁工程实用计算提供了一种简单方便的方法。

连续组合梁负弯矩区开裂之后应力释放，在挠度增加不大的情况下出现有利的弯矩重分布(负弯矩减幅达20%以上，正弯矩增幅约16%)，而徐变会缓解开裂重分布弯矩和应力释放程度。还须重视的是徐变会明显增加连续梁的跨中挠度，在型钢牌号小的情况增幅更显著。