DC-SQUID串联阵列直流特性研究

姜稣仆 杨瑾屏 张 硕 任翠兰 怀 平,,5 伍文涛

1（中国科学院上海应用物理研究所 上海201800）

2（中国科学院大学 北京100049）

3（上海科技大学大科学中心 上海201210）

4（中国科学院上海微系统与信息技术研究所 上海200050）

5（中国科学院上海高等研究院 上海201204）

21世纪是生命科学、物质科学、能源科学及环境科学等学科飞速发展的时代，这些科学研究对在亚纳米空间分辨率与飞秒时间分辨率下研究复杂体系提出了更高的目标和要求。X射线正是研究这些学科的重要工具之一，因此，这一需求推动了大型同步辐射［1-2］和自由电子激光用户装置［3-4］的飞速发展。我国已于2018年开始建设上海硬X射线自由电子激光装置（Shanghai Hard X-ray Free Electron Laser Facility，SHINE）的大科学工程项目，SHINE是目前国际上性能优异的大型硬X射线自由电子激光装置，能够发出0.01～0.1 nm的硬X射线，在亮度、相干性以及超快特性等方面有着突出优势，能够为化学、物理、材料、生物等诸多科学领域提供更高的分辨率成像、更先进的结构解析和超快过程探索等尖端科研手段。

超导转变边缘探测器是将超导转变边缘传感器（Transition Edge Sensor，TES）作为温度计的一类低温超导探测器，其同时具备高能量分辨能力（1 eV量级）及高量子效率（90%以上）的特点，探测范围从近红外到γ射线，成为SHINE装置上部署的一类高灵敏度探测器［5］。然而，TES的电阻一般在欧姆以下量级，很难使用场效应管等实现阻抗匹配和放大。为解决这个难题，科学工作者引入超导量子干涉器件（Superconducting Quantum Interference Device，SQUID）作为TES的低温读出电路［6］。

SQUID是迄今为止最为灵敏的磁场/电流传感器，具有逼近量子极限的噪声性能，如非耦合型DCSQUID的磁通噪声水平可达10-6～10-7Φ0/Hz。但单个DC-SQUID的输出电压仅在μV量级。为进一步对这一信号进行低噪声高增益放大并与室温端读出电路实现阻抗匹配，第二级DC-SQUID串联阵列电路被采纳。DC-SQUID串联阵列是将N个相同的DC-SQUID器件串联在一起，并借助磁通反馈环路将其偏置在具有最大转换增益的工作点，使得DCSQUID串联阵列的电压可以达到接近mV的输出。目前单个DC-SQUID的理论研究和实验测试已经十分广泛，但针对DC-SQUID串联阵列的建模和噪声分析尚未有全面深入。

本文针对DC-SQUID串联阵列的直流特性开展了理论分析和实验研究。

1 DC-SQUID串联阵列直流特性理论分析

1.1 DC-SQUID串联阵列的直流I-V曲线

DC-SQUID串联阵列是由N个完全相同的DCSQUID串联而成。若不考虑DC-SQUID环路电感和Josephson结电容，并拟定DC-SQUID串联阵列中每个Josephson结都完全相同，每个环路的内部磁通都为零，则根据Josephson结的RSJ模型［7］，可以建立DC-SQUID串联阵列的直流等效电路模型，如图1（a）所示。其中，RP是单个Josephson结的结区并联电阻；IC是单个理想Josephson结的临界电流；Φi是单个DC-SQUID的位相差（i=1，2，…，N），RS是DC-SQUID之间连线以及外部连接线等所有非超导态连线的总电阻。根据超导隧穿理论可以建立描述DC-SQUID串联阵列直流I-V曲线的关系方程式：

由式（1）和（2）可以解出理想情况下单个Josephson结两端平均电压与偏置电流I之间的关系：

将其与式（3）联立，可以得到整个DC-SQUID串联阵列的直流I-V曲线，满足以下关系：

由以上方程结果可知，如果将整个DC-SQUID串联阵列视为一个大的Josephson结，则串联阵列临界电流IC，SA等于2IC，而串联阵列正常态电阻RP，SA等于N·RP/2。因而，其I-V曲线如图1（b）所示。

从图1（b）的I-V曲线可以看到，RS可以由偏置电流小于Josephson结临界电流部分的曲线斜率确定，而串联阵列正常态电阻则不能直接计算。现令V"=V-IRS，则式（5）可变换成以下关系式：

图1 DC-SQUID串联阵列直流等效电路模型(a)和I-V曲线(b)Fig.1 Direct current equivalent circuit model of DC-SQUID series array(a)and I-V curve(b)

为了更容易进行参数提取，对式（6）平方则获得以下形式：

由此可见，DC-SQUID串联阵列的I2-V′2曲线应为一条直线。其中，直线斜率为DC-SQUID串联阵列正常态电阻RP，SA的平方，与I2轴交点为DCSQUID串联阵列正常态电阻RP，SA与临界电流IC，SA乘积的平方。由此，可以通过实测的I-V曲线计算得出以上三个DC-SQUID串联阵列电路模型参数。

1.2 高斯白噪声对DC-SQUID串联阵列直流I-V曲线的影响

根据BCS理论，超导体中的Copper对处于最低能级，由Copper对组成的超导电流在超导体中流动或者从Josephson结隧穿时并不会产生噪声现象。但处于非绝对零度的超导体中实际上同时存在Copper对和准粒子两种不同的载流子。由准粒子形成的正常态电流不仅体现为Josephson结区电阻，同时也会产生热噪声。当准粒子从Josephson结隧穿时则会产生散粒噪声。此外，超导体中的Copper对不停地激发变成准粒子，而具有相反动量的准粒子也在不停地复合为Copper对，两者载流子处于动态平衡中。这种破裂-复合过程也会产生噪声。这些噪声在低频下都表现出高斯白噪声特性。因而，对于单个DC-SQUID，其I-V曲线关系方程将变成：

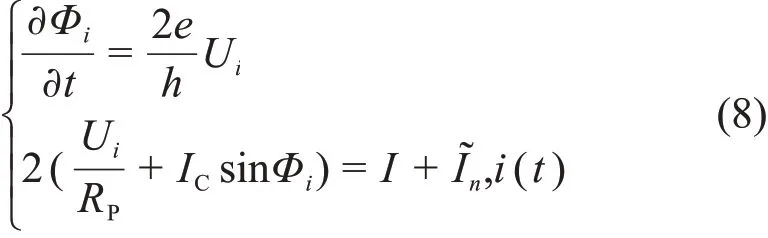
其中，高斯白噪声统计性质满足=0，=2Dδ(t1-t2)，D为 噪 声 强度。于是在噪声影响下DC-SQUID串联阵列的电流和输出电压本质上也都是随机变量。其物理随机过程可以表述成朗之万方程形式：

通过求解与朗之万方程等效的福克-普朗克方程，最终单个DC-SQUID的平均电压可以由下式计算：

也可以将其表述成由DC-SQUID串联阵列临界电流IC，SA和串联阵列正常态电阻RP，SA组成的形式：

DC-SQUID串联阵列I-V′曲线受器件自身的高斯白噪声影响可以参见图2。从高斯白噪声参量γ的定义可知其与噪声强度D为反比关系，因此，γ越小则噪声越大。当γ为无穷大时，DC-SQUID串联阵列特性不受噪声影响，I-V′曲线正如式（6）所示。当γ变为有限值时，DC-SQUID串联阵列I-V′曲线受到噪声影响而出现“圆拱化”。γ越小，I-V′曲线越接近于直线。而I-V′曲线上表征输出电压从零伏开始的临界电流也明显小于真实的临界电流。但从图2可以看到，当γ>100时，DC-SQUID串联阵列I-V′曲线仅在临界电流附近受到影响；而当偏置电流明显大于临界电流时则与理想情况（γ为无穷大）十分接近。因此，对于包含噪声影响的DC-SQUID串联阵列IV′曲线，其真实的临界电流仍可通过式（7）进行参数提取。

图2 DC-SQUID串联阵列I-V′特性受高斯白噪声参量γ影响的数值计算结果(I C,SA=20μA,R P,SA=10Ω)Fig.2 Numerical calculation results of I-V′characteristics of DC-SQUID series array with the influence of Gaussian white noiseγ(I C,SA=20μA,R P,SA=10Ω)

2 DC-SQUID串联阵列直流特性的实验测试与分析

2.1 实验测试系统

如图3（a）所示，本文所使用的测试系统可以分为低温单元和常温单元两部分。低温单元由DCSQUID串联阵列芯片、低温邦定线、连接线缆和低温杜瓦等组成。常温单元由数控恒流源、前置放大器和高速数据采集系统等组成，实现信号的放大、成形和对外输出［8］。数控电流源提供DC-SQUID工作所需的恒定偏置电流，前置放大器则将DC-SQUID输出的微伏（μV）量级电压信号进行低噪声放大，再由数据采集系统（Data Acquisition System，DAQ）变换成数字信号并记录保存。其中，数控恒流源的电路设计是由美国ADI公司的14位数模变换器（Digital to Analog Converter，DAC）芯片AD7568和高精度限流电阻（R0=10.0 kΩ）串联而成。由于限流电阻的阻值远大于连接线电阻以及DC-SQUID等效电阻等之和，因而偏置电流大小几乎完全由DAC的输出电压决定，而不受DC-SQUID自身实际工作状态的影响，其具体值可由I=U/R0计算。数据采集系统采用美国NI公司的PXIe-6358 16位100 kHz高速采集卡，并使用LabVIEW编程控制。前置放大器提供了5 000倍的低噪声电压放大，电路原理框图如图3（b）所示。其中运算放大器A1、A2和A3组成经典三运放仪表放大器结构，A4则提供反相放大功能。仪表放大器具有极低的差模输入噪声、温度漂移和较高的输入阻抗，以及极大的共模抑制比。在进行电路设计时，运放的选型十分关键［9］。运算放大器A1、A2采用的是美国ADI公司的AD797，是目前为止噪声最低的常温器件之一。输入端的电压噪声小于1.0 nV/Hz，输入端的直流噪声总和小于0.32μV，能够较好保证DC-SQUID串联阵列输出信号的信噪比。此外，该运算放大器还具有专用于调节输入失调电压的管脚，可以将由前置放大器单元自身产生的直流电压偏移影响降到最低程度。

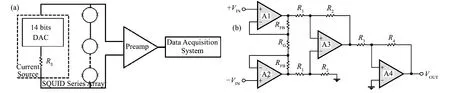
图3 DC-SQUID串联阵列的测量系统框图(a)和前置放大器原理框图(b)Fig.3 Block diagram of DC-SQUID series array test system(a)and preamp schematic(b)

2.2 结果与讨论

以二阶DC-SQUID中用于第二级放大的串联阵列在65 mK温度下的实测I-V曲线为例，直流偏置下可以忽略环路电感和结电容的影响，符合RSJ模型的建立条件。根据式（5）和（6），采用最小二乘法拟合出该DC-SQUID串联阵列的IC，SA、RP，SA和RS，再根据式（12）拟合出高斯白噪声参量γ。实测I-V曲线和根据表1参数结果由式（6）和式（12）进行数值计算得到的结果可以参见图4。从图4可以看到，式（12）的计算结果与实测I-V曲线符合得非常好，从而证明了本文提出DC-SQUID串联阵列电路模型和噪声分析理论的有效性。

若拟定高斯白噪声完全由DC-SQUID串联阵列内的Josephson结的电阻热噪声贡献，则噪声强度可以由式（13）计算：

表1 DC-SQUID串联阵列参数Table 1 Parameters of DC-SQUID series array

图4 DC-SQUID串联阵列实I-V曲线及参数数值计算结果Fig.4 I-V curve of DC-SQUID series array and the results of parameter calculation

此时温度T对应的白噪声参量γ值可由式（14）计算。

根据表1所给各项参数计算结区的电阻热噪声γ的理论值为8.63×103，远大于实验拟合值。这说明在65 mK温度下DC-SQUID串联阵列内部的噪声的主体不是结区的电阻热噪声。另外，也可以将高斯白噪声视为某种散粒噪声，则可以根据下式计算出它的Fano因子：

根据上述实验参数，可以算得此时Fano因子值为37.4，远大于1。对这一结果，本文从理论和实验两方面分析了可能的原因：

1）本文拟定DC-SQUID串联阵列中的每个DCSQUID单元相互独立，仅受内部噪声影响。但实际上由于DC-SQUID串联阵列的单元尺寸很小且距离非常近，有可能出现多个Josephson结信号的相干，这种情况下的载流子输运噪声应该考虑多重Andreev反射效应，有可能出现Fano因子远大于1的情况［10］。

2）本文在建立分析理论时拟定DC-SQUID感应到的内部磁通为零。而实际上DC-SQUID是非常灵敏的磁场传感器，且该DC-SQUID串联阵列中DCSQUID单元的数目是32。因此，虽然实验已经采取了诸多措施屏蔽周围磁场，但DC-SQUID串联阵列仍可能拾取残余磁场噪声的影响，譬如地磁或电机等大型仪器设备产生的强电磁场。

3 结语

本文基于Josephson结的RSJ模型建立了一种适用于DC-SQUID串联阵列的直流电路模型和I-V关系方程式，并利用福克-普朗克方程研究了高斯白噪声对DC-SQUID串联阵列I-V曲线的影响。实测DC-SQUID串联阵列芯片的数据验证本文所给解析计算公式的正确性。同时，本文实测结果发现DCSQUID串联阵列具有超高Fano因子，这有待通过进一步理论研究和实验结果加以分析。