云计算环境下基于全同态加密的人脸信息保护
徐慧华,杨 雄,张晓惠
(1.福建师范大学协和学院 经济与法学系,福建 福州 350117;2.福建师范大学协和学院 区域特色产业与普惠金融协同创新中心,福建 福州 350117;3.福州大学至诚学院 计算机工程系,福建 福州 350002)
人脸识别是通过人工智能技术从人脸中提取脸部特征信息,并根据这些特征对人的身份进行识别的一种生物识别技术。和其他生物识别技术相比,人脸识别由于其独特的优势:非接触性、自然性、不易察觉性和并发性,已广泛应用于金融领域中。比如在银行和证券系统中,客户在办理业务时使用人脸识别技术,可以快速方便确定客户身份,提升业务办结效率,不仅减轻了运营负担,而且能够有效进行风险控制。目前,依托于人工智能和大数据的快速发展,人脸识别的准确性快速提高,已处于较高水平,其识别效果甚至超过了人类识别的程度。在当今大数据时代,如果个人的人脸信息与该主体的其他信息相关联,那利用人脸信息就很容易识别特定的主体,从而轻易获取该主体的其他信息。由于个人信息蕴含有极大的商业价值,这也成为众多企业过度收集、存储和使用人脸信息的动力。广泛应用的人脸识别技术使得采集和存储人脸信息的数量和规模不断膨胀,如果该信息被泄漏或被非法人员获得,将可能会产生严重的信息安全问题[1]。
2020年5月28日第十三届全国人民代表大会第三次会议通过的《中华人民共和国民法典》,其中第六章专设了对隐私权和个人信息的保护规定。全国人大常委会也明确将个人信息保护法纳入2020年度的立法工作计划。在数字经济时代,人脸识别的个人信息大数据遍布各种应用场景,产生越来越多的个人信息数据。但由于对数据信息的监管薄弱,缺乏大数据个人信息保护的技术支撑,所以个人信息保护在大数据时代受到了空前的挑战[2]。
因此,除了在法律层面构建起人脸特征信息的保护体系外,还应该从数据和技术等维度更有针对性地规制该技术,从而更好地保护个人信息。
1 云计算环境下的人脸识别
随着人脸识别应用的需求激增,人脸图像数据库的规模也同时不断膨胀。作为新兴技术的云计算,是一种可以很好解决人脸图像膨胀产生的时间复杂度和空间复杂度增加的途径。
基于云计算的人脸识别系统是为用户提供高效、高精度人脸识别的工具。基于云计算平台的人脸识别系统框架如图1所示。其中,离线学习部分是把人脸图像源的图像通过检测、定位和预处理后,提取出人脸特征值并存储于HBase人脸数据库中。在线识别部分也是先将待识别人脸图像通过检测、定位、预处理和提取人脸特征后,将待识别人脸图像的特征与 HBase 人脸数据库中的特征进行分类比较,最终得出人脸识别的结果。离线学习部分和在线识别部分的人脸检测与定位、预处理、特征值向量提取步骤的算法是一致的。系统中的人脸检测与定位、人脸图像预处理和特征值与特征向量提取步骤一般是在用户端进行,分类器和HBase人脸图像数据库则是部署在云计算环境下的。
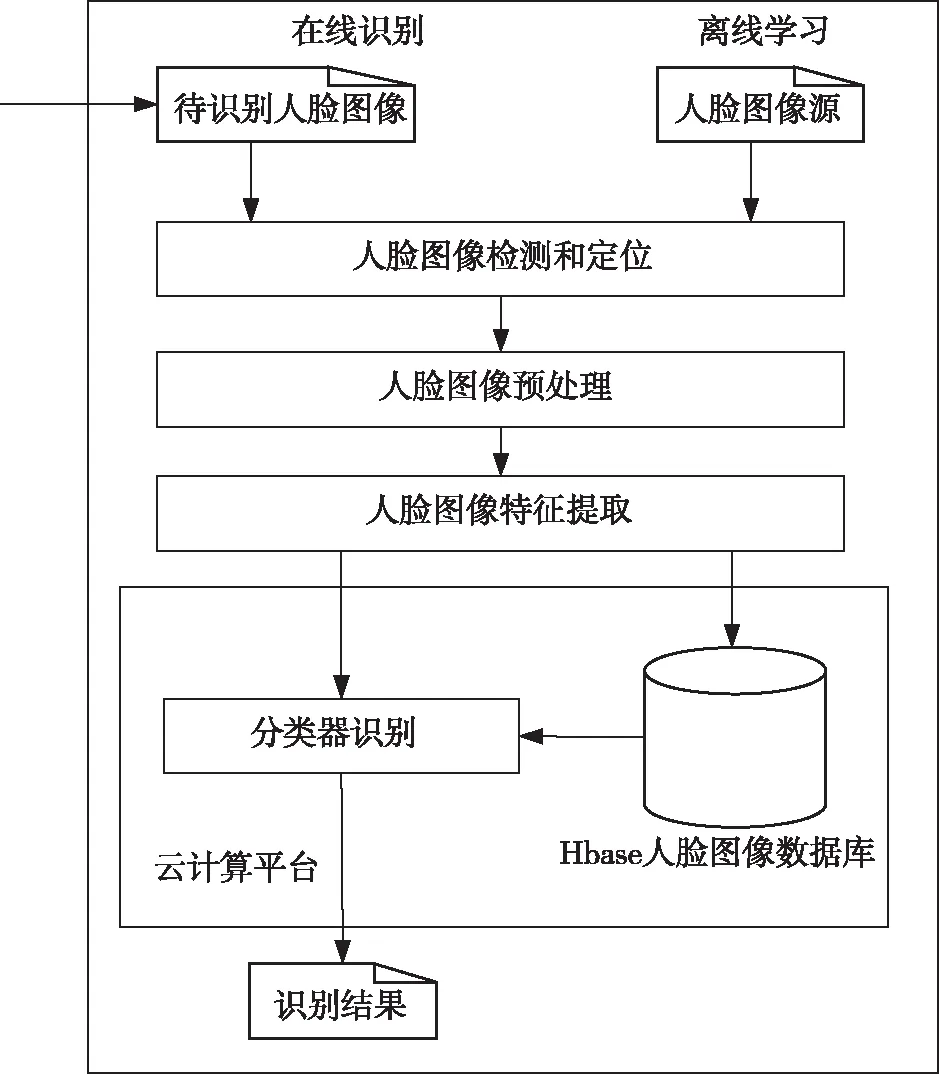
图1 云计算环境下的人脸识别系统结构图
但在现有云计算环境下的人脸识别系统中,对系统中人脸特征的保护甚少[3],用户的人脸特征一般直接以明文表示。此时,存储于数据库中的人脸特征和用户注册与身份认证过程中网络传输的人脸特征一旦泄漏,就会严重影响注册用户的隐私和认证系统的安全性。因此,对于云计算环境下的人脸识别系统最直接的攻击就是明文形式的人脸特征。随着对信息安全和隐私保护要求的不断提升,针对云计算环境下的人脸识别系统设计一种安全的人脸特征保护方案则显得尤其重要。
2 全同态加密技术
为了提升人脸识别系统的安全性,避免人脸特征明文信息的泄漏,可通过密码系统对人脸特征信息进行加密。但若采取普通的加密方案,在计算人脸特征向量间相似度时,需要对密文进行解密,还是会存在人脸特征信息泄漏的风险。而同态加密方案能够在密文环境下直接对加密的人脸特征向量进行算术运算,可以恢复出明文的运算结果,因此在计算人脸相似度过程中不需要对人脸特征密文进行解密,避免了人脸特征信息的泄漏。同态加密是一种对称加密算法,由GENTRY等[4]发明提出。其同态加密方案包括4个算法,即密钥生成算法、加密算法、解密算法和额外的评估算法。同态加密包括两种基本的同态类型,即乘法同态和加法同态。同态加密系统按照同态加密算法支持的运算类型和数量,将其分成 3 类:部分同态加密[5]、层次同态加密[6]和全同态加密[7]。部分同态加密(partially homomorphic encryption, PHE)指同态加密算法只对加法或乘法(其中一种)有同态的性质。 层次同态加密算法(somewhat homomorphic encryption,SWHE)一般支持有限次数的加法和乘法运算。全同态加密算法(fully homomorphic encryption, FHE)支持在密文上进行无限次数的、任意类型的计算。FHE 的优点是支持的算子多并且运算次数没有限制,在实际场景中更为通用;但缺点是计算复杂度较高,效率偏低,尤其是其中的乘法运算。
全同态加密方案保证了数据处理服务器在计算人脸相似度时无法知晓所处理人脸特征的明文信息,可以直接对数据的密文进行相应的计算,由此用户的人脸特征信息可以得到相应的安全保障。数据处理服务器计算出加密人脸特征间的相似度后,把结果返回。在整个计算过程中,数据处理服务器仅仅得到加密后的人脸特征向量数据,而对于人脸特征向量数据的明文,其并不知晓。因此,就不存在人脸特征信息泄漏的风险。同态加密的实现效果如图2所示:
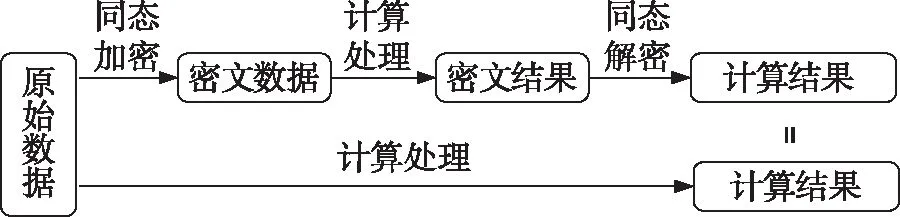
图2 同态加密的原理图
本文基于全同态加密技术对人脸特征向量进行加密,构造了密文环境下人脸特征相似度的匹配算法,并在此基础上设计了一种隐私保护的高效人脸认证方案。该方案不仅保证了原生人脸认证方案准确率,还保证用户的人脸特征信息在身份认证过程中不被泄漏。进一步,探索了基于中国剩余定理(Chinese remainder theorem,CRT)实现了一种加密向量的批量点积运算,提高了人脸相似度的计算效率。最后,基于人脸基准数据库(labeled faces in the Wild,LFW)设计了研究性测试环节。通过测试环节验证了该方案的可行性和高效性,能够满足实际场景的应用需求。
3 基于全同态加密的人脸识别方案
3.1 人脸图像特征的提取算法
近年来,快速发展的基于深度学习的人脸识别算法已占据当今人脸识别领域的主导地位,在 LFW 上的识别率已经接近 100%,远远超过传统的人脸识别算法[8]。本文选取其中最具代表性的FaceNet[9]和SphereFace[10]作为系统原型中的人脸特征提取算法。
FaceNet算法基于深度卷积网络将人脸图像映射到欧几里德空间后,通过计算其欧氏距离来获得人脸特征间的相似度。若计算得到的距离小于设定阈值,则认为两张图片的相似度较高,是属于同一个人的不同脸部图片。与其他使用深度神经网络的人脸识别方法不同,FaceNet人脸识别算法是直接使用基于triplets的最大边界近邻分类的损失函数来训练神经网络,并输出一个512维的向量空间,可大大提升人脸识别的效率。
SphereFace基于归一化权值和角度间距,提出对传统的 softmax 进行改进的新损失函数A-Softmax Loss(Angular Softmax Loss) ,实现了最大类内距离小于最小类间距离的识别标准。SphereFace算法以两个人脸特征向量间的余弦值作为相似度度量,余弦值给出的相似性范围从-1到1,-1表示这两个向量的指向正好截然相反,1表示它们的指向是完全相同的,而这两者之间的值则表示中间的相似性程度。SphereFace算法根据向量间的余弦值是否大于给定的阈值来判断两个人脸信息是否属于同一个人。
3.2 全同态加密算法
全同态加密方案主要包含以下5个步骤:
1) GenKey (λ):生成一对公私钥。根据输入的安全参数生成公钥θp和私钥θs。
2) Encrypt (m,θp)
使用公钥θp加密消息m,计算生成密文c。
3) Add(c0,c1)
输入两个密文c0和c1,计算求得这两个密文的和c0+c1。
4) Multiply(c0,c1)
输入两个密文c0和c1,计算求得这两个密文的乘积c0×c1。
5) Decrypt (c′,θs)
根据密文c′,利用私钥θs计算出明文m′。
本文选择主流的全同态加密库Microsoft Seal库。Seal库支持两种加密方案: BFV方案[11]和CKKS方案[12]。其中,BFV支持整数,CKKS支持浮点数。SEAL采用的同态加密算法基于多项式环。BFV 方案中有3个重要的参数:多项式模次数(poly_modulus_degree)、密文系数模(coeff_modulus)和明文模(plain_modulus)。
其中,多项式模次数是影响同态加密方案安全性的主要因素,是必须设置的。多项式模次数越大,虽然方案的安全性越高,但密文也随之增大,会导致同态操作的计算效率降低。在 Seal 库中,推荐的次数是1 024、2 048、4 096、8 192、16 384、32 768。但由于小于4 096时不支持循环旋转加密向量,因此需要选择4 096以上的多项式模次数。而且明文的槽数(单个明文向量的最大维度)与多项式模次数的大小一致。
密文系数模是一个大整数,它是不同素数的乘积,更大的密文系数模意味着更大的噪声预算,支持更多次的同态计算。然而,多项式模次数确定了密文系数模总比特长度的上限。比如4 096对应109,8 192对应218。Microsoft Seal提供了用于选择密文系数模的辅助函数。
明文模可以是任何正整数。明文模决定了明文数据的大小, 同时也影响了噪声预算消耗。新加密密文的噪声预算是log2(密文系数模/ 明文模)(位),一般认为加法在噪声预算消耗方面几乎是免费的,但乘法的噪声预算消耗为log2(明文模)+(other terms),一旦密文的噪声预算达到零,它就会被破坏得无法解密。因此,必须选择足够大的密文系数模或者尽量保持明文尽可能小来支持所需的计算;否则,即使使用密钥,结果也不可能有意义。通过人脸特征提取出来的各个特征值为浮点数,因此使用BFV方案时还需要将各个特征值通过扩大因子转换为整数。为了保证计算结果的准确率,扩大因子当然是越大越好。但每个明文槽只包含一个整数模的明文模量,除非明文模量非常大,否则可能会遇到数据类型溢出问题,溢出问题并不能以加密的形式检测到。可以通过直接增加明文模来避免溢出问题的发生,但是增加明文模则会增加噪声预算消耗,同时降低初始噪声预算。
与BFV方案不同的是,CKKS 方案不使用明文模。虽然CKKS方案可解决数据类型溢出问题,但代价是计算结果只产生近似的结果,而且还需要额外对浮点系数进行缩放操作;同时它的明文槽数为多项式模次数的一半,意味着同样的参数下CKKS方案的批量处理能力仅为BFV方案的一半。
本文将分别探寻两种方案下的较优参数,给出BFV和CKKS方案下的准确率测试和直观的性能分析。
3.3 基于全同态加密的人脸特征相似度计算
3.3.1欧式距离的全同态加密计算
在人脸特征向量未加密的情况下,假设身份认证凭证的特征向量为X,数据库中待计算的某个人脸特征向量为Y,那么将X和Y之间的相似度定义为:
(1)
其中,n为所提取的人脸特征维度。
从公式(1)可知,人脸特征向量欧氏距离的计算过程包含了n个向量元素的减法(Xi-Yi)、n个向量元素的乘法(平方)和n个向量元素的累加求和。
按照传统的密码学方案,对特征向量中的每个元素进行单独加密。那么,对人脸特征向量中的元素加密后,公式(1)中描述的人脸相似度在加密域中描述为:
(2)
其中,cXi和cYi分别为特征向量X和Y的元素密文。
加密域人脸相似度的同态计算可分为3个步骤:
1)对相应的特征向量元素密文进行减法运算,如:cZi=Add(cXi-cYi);
2)对特征向量元素密文减法运算的结果进行平方(乘法)运算,如:cZi=Multiply (cZi,cZi);
3)最后,再对cZ的各个特征向量元素的密文进行累加,得到欧式距离的平方。由于全同态加密不支持平方根操作,因此,在加密域中仅求得欧式距离平方的密文。
综上,在加密域中计算欧式距离需要2n-1次的同态加法和n次的同态乘法运算。
3.3.2余弦相似度的全同态加密计算
类似地,特征向量X和Y之间的余弦相似度定义为:
因为向量长度值并不会包含具体的人脸特征信息,因此,可以在人脸特征提取后直接计算人脸特征向量的长度,将人脸特征向量长度值和人脸特征共同存储于数据库中,那么人脸特征余弦相似度的计算公式可简化为:
(3)
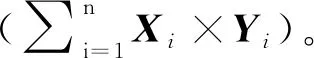
公式(3)中描述的人脸特征向量余弦相似度在加密域中描述为:
(4)
同样地,在加密域中计算人脸特征间的余弦相似度需要n次的同态乘法和n-1次的同态加法运算。
3.3.3人脸特征相似度同态计算的准确率
在全同态加密方案中,首先生成一对公私钥:公钥θp和私钥θs;然后通过加密函数f对人脸特征X进行加密:ε(X)=f(X;θp),同时满足X=g(ε(X);θs),其中,g为解密函数。基于全同态加密的人脸相似度在保护人脸特征安全性的基础,还要保证在加密域中进行同态计算后尽量不损失精度,即:
sim(ε(A),ε(B))=sim(f(x;θp),f(y;θp))
g(sim(ε(A),ε(B));θs)≈sim(A,B)
其中,sim()表示欧式距离或者余弦相似度。
3.4 批处理方案
按照上述分析,人脸相似度的计算方法可直接应用于加密域,但它的同态计算的复杂性却无法满足实际应用的要求。以512维的人脸特征为例,每个特征向量至少需要16.5 MB的存储空间,同时一次人脸的相似度计算也需要至少消耗0.7 s的计算时间。BRAKERSKI等[13]提出一种以数字向量为原子单位进行同态加密和解密的方法,该方法利用了中国剩余定理(Chinese Remainder Theorem, CRT) ,将数字向量中的n个元素编码到同一个多项式上。如此就可以将n维的人脸特征向量进行整体加密,并将n个向量元素密文的加法和乘法操作转换为单个向量密文的加法和乘法操作,即在单次同态计算操作的时间内完成了n次同态加法或乘法运算,可显著提高计算效率。
两种人脸相似度的计算过程中都涉及到n个向量元素的累加求和操作,但批处理方案是对向量整体进行加密,倘若要对各个向量元素进行累加求和,就需要先解密,这与本方案的目标相违背。该局限性可通过GENTRY提出的循环旋转操作来解决。在加密域中,通过向左循环旋转logn次向量密文并累加,就可以获得向量密文中的各个元素的累加和。
以简单的4维向量密文为例,第i次对累加后的向量向左循环i次,那么通过循环旋转2=log 4次,就可以计算出该4维向量密文的各分量之和。具体过程如图3所示:
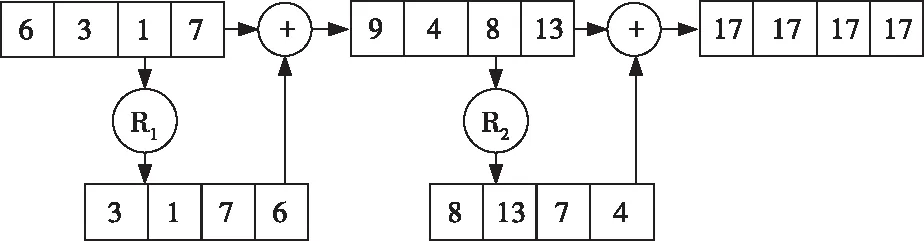
图3 循环旋转计算向量累加和
对于512维的人脸特征向量,原先511(n-1)次同态密文的加法运算,现在只需9次的循环和加法运算,既降低了计算复杂度,又可以在加密域中实现密文向量元素的累加和操作。
3.5 系统原型设计
基于全同态加密的云计算环境下的人脸识别系统的框架如图4所示,在提取出人脸特征向量后使用公钥进行全同态加密。并引入了可信计算节点,将全同态密文的计算结果在可信计算节点中使用私钥进行解密。
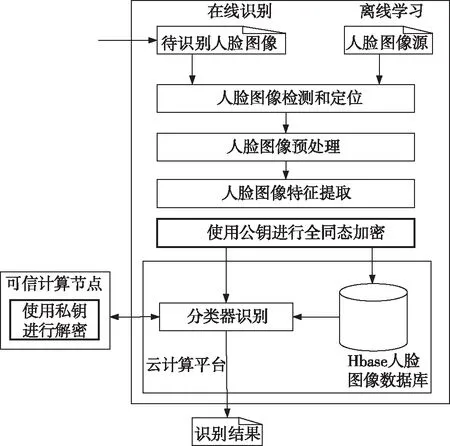
图4 云环境下基于同态加密的人脸识别应用原型
4 实验结果与分析
在系统仿真测试中,从LFW数据库中随机选择6 000对人脸组成了人脸辨识图片对,其中3 000对属于同一个人2张人脸照片,3 000对属于不同的人每人1张人脸照片。分别通过SphereFace和FaceNet算法,提取出测试数据集中所有人脸的512维特征向量。在全同态加密下计算6 000对人脸特征向量间欧式距离和余弦相似度,将计算结果与未加密的计算结果进行对比,以此作为同态加密方案准确率的估算。仿真测试环境中,认证服务器的计算集群使用单台云服务器,服务器配置为四核8 G,CPU型号为AMD EPYC 7K62 48-Core。
4.1 公钥和私钥生成测试
全同态加密算法的公私钥文件的大小与多项式模次数和密文系数模的参数高度相关,而多项式模次数又确定了密文系数模总比特长度的上限,因此一旦多项式模次数确定,那么公私钥文件的大小也就确定了。
多项式模次数越大,虽然方案的安全性越高,但密文也随之增大,会导致同态操作的计算效率降低。因此在测试中,多项式模次数的参数为4 096和8 192。公私钥文件的生成时间也与多项式模次数高度相关。生成公私钥文件的大小和生成时间的描述性统计如表1所示:
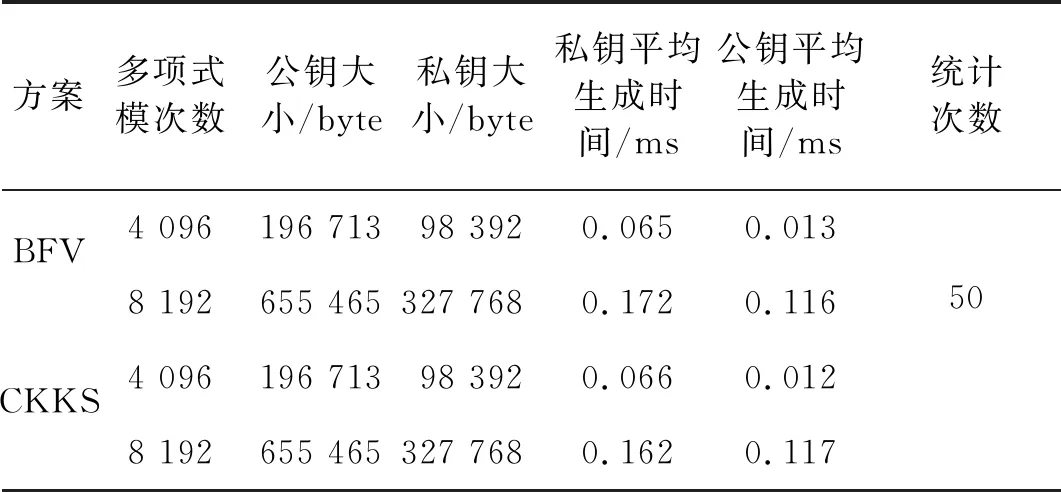
表1 公私钥文件大小和平均生成时间
4.2 加密测试
单个明文的最大维度(明文的槽数)与多项式模次数的大小一致,为了最大限度地利用存储空间和提高批处理的能力,可将多个人脸特征向量编码进同一个明文中,以BFV方案中多项式模数4 096为例,其明文槽数也为4 096,单个人脸特征向量维度为512,因此可同时将8个人脸特征向量编码进同一个明文中。
生成公私钥文件后,分别对6 000对人脸进行加密。各个参数下的加密时间和加密前后文件大小的统计如表2所示:
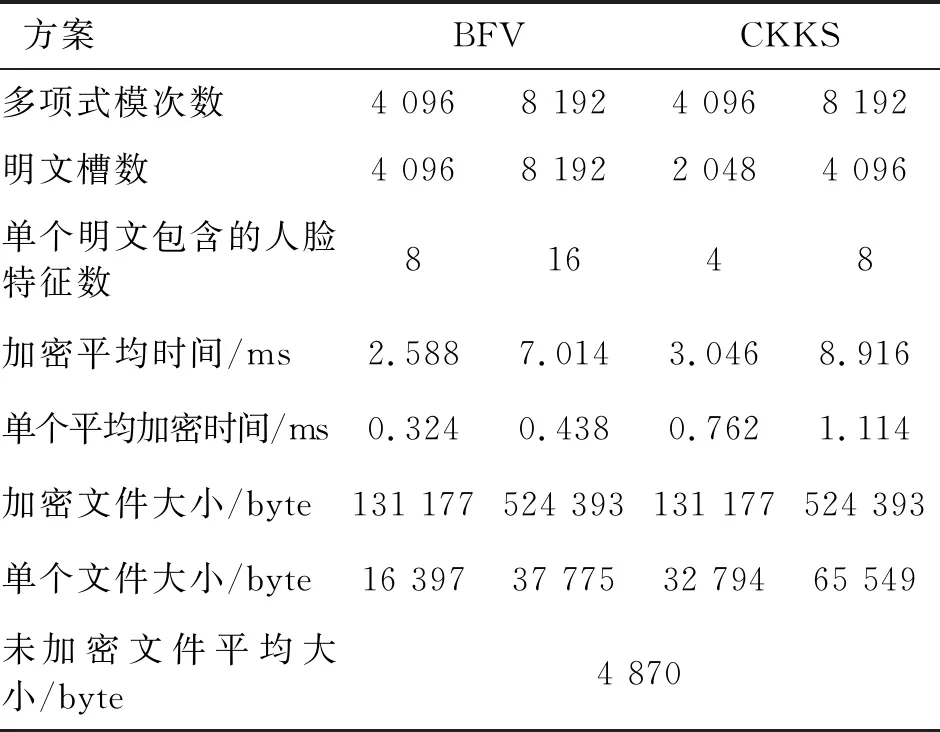
表2 加密时间统计和加密前后文件大小
4.3 人脸相似度的同态计算测试
由于BFV方案中全同态加密先对人脸特征值编码为整数后才进行操作,因此先对人脸特征值乘以扩大因子,待求得计算结果再对结果进行缩放。
根据人脸相似度进行身份识别时,FaceNet算法的阈值为0.864,SphereFace算法的阈值为0.305。
1) FaceNet算法
BFV方案多项式模数为4 096时,不同扩大因子(factor)下人脸识别准确率如图5所示:
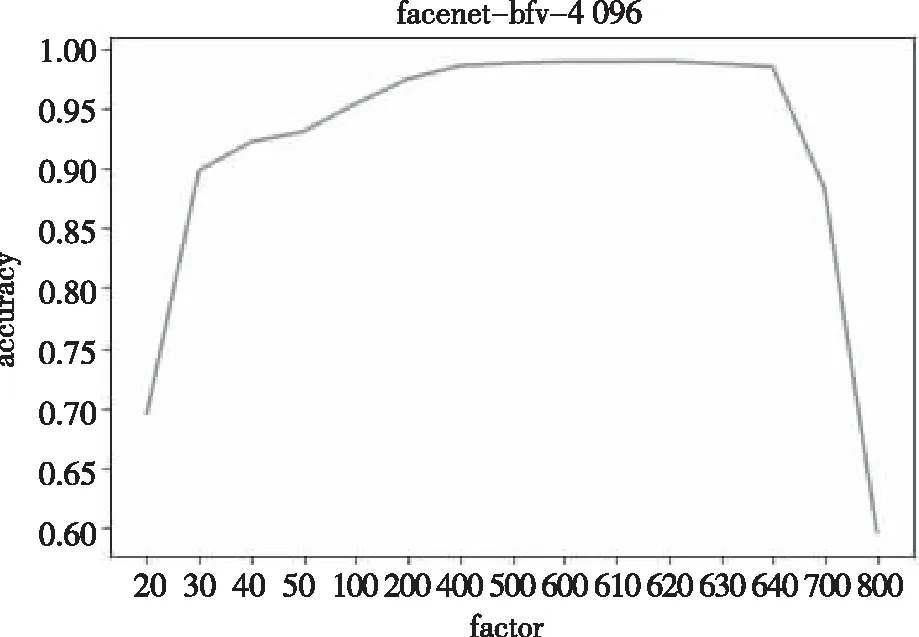
图5 多项式模次数为4 096的准确率变化曲线
随着扩大因子的增大,计算结果的精度不断增大。当扩大因子达到620时,达到未加密情况下人脸识别准确率的98.98%,非常接近于FaceNet算法未加密时准确率。但随着扩大因子的继续加大,出现了向量中各个元素密文的累加和的数据类型溢出,导致准确率急剧下降。
当多模式模数为8 192时,密文系数模总比特长度上限相应提高,在面对同样的数据操作时,由于支持更大的噪声预算,所以可解决数据溢出的问题。这意味着该参数下支持更大的扩大因子,也就能够达到更高的人脸识别的准确率。BFV方案多项式模数为8 192时,不同扩大因子(factor)下人脸识别准确率如图6所示。
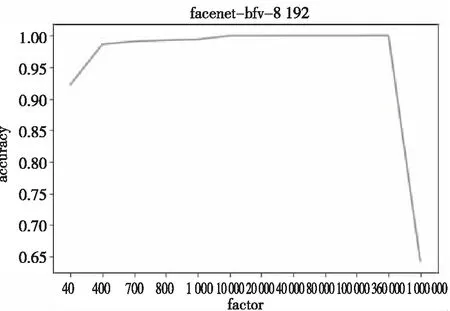
图6 多项式模次数为8 192的准确率变化曲线图
与多项式模数为4 096的折线图类似,随着扩大因子的增大,计算结果的精度不断增大。但该参数支持更大的扩大因子上限,当达到360 000时,其人脸识别的准确率达到了未加密时的准确率。观察其计算结果,与未加密时的计算结果误差在1e-5,但不影响识别的准确率。之后,随着扩大因子的继续增大,一样会发生数据类型溢出的问题,同样人脸识别的准确率会下降。与参数4 096相比,其能够达到未加密时的准确率,但其付出的代价为计算性能的下降。
CKKS方案提供了一个“rescale”功能,因此还需要配置scale参数。该参数在多项式模次数为4 096时配置为30,在8 192时配置为40。由于CKKS方案是支持浮点数运算的,因此不需要使用扩大因子对人脸特征进行预处理,可直接进行运算。在两个参数下,其人脸识别的准确率都达到了未加密时的准确率。
FaceNet算法下两种同态方案不同参数下的人脸相似度的同态计算时间统计如表3所示:
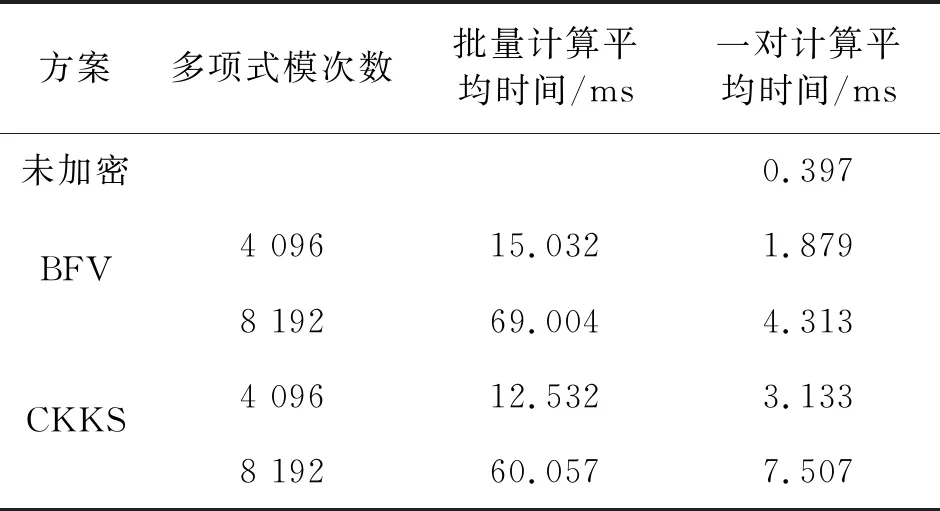
表3 FaceNet算法人脸相似度同态计算的时间统计
2)SphereFace算法
类似地,BFV方案4 096和8 192参数下不同扩大因子(factor)下人脸识别准确率变化如图7所示。
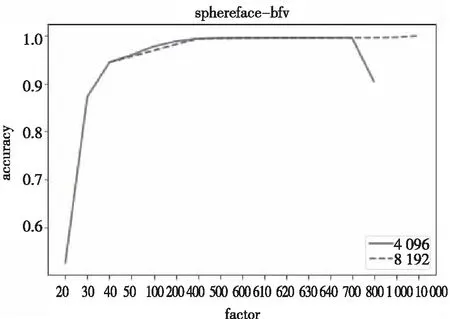
图7 BFV方案的准确率变化曲线
同样地,CKKS方案下4 096和8 192参数下的人脸识别的准确率也都达到了未加密时的准确率。
SphereFace算法下两种同态方案不同参数下人脸相似度的同态计算时间统计如表4所示。
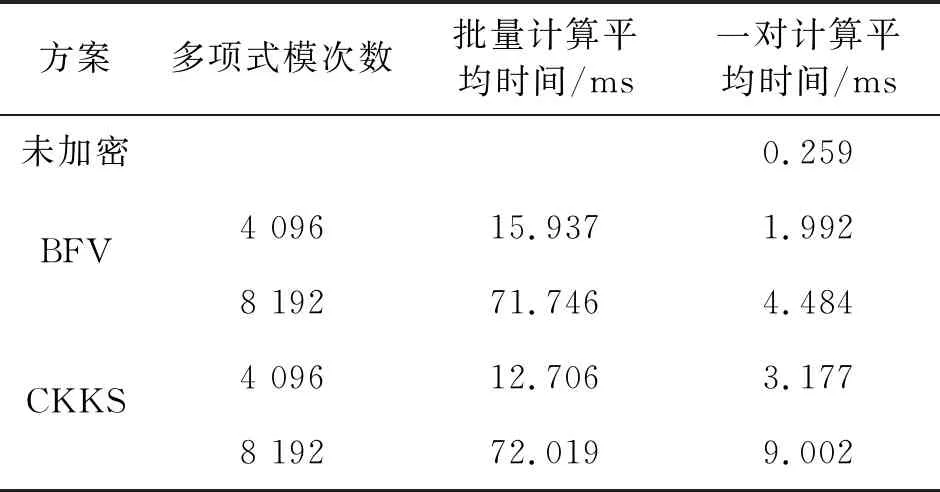
表4 SphereFace算法人脸相似度同态计算的时间统计
4.4 解密测试
对不同参数下的计算结果进行解密,各个参数下的解密时间统计如表5所示:
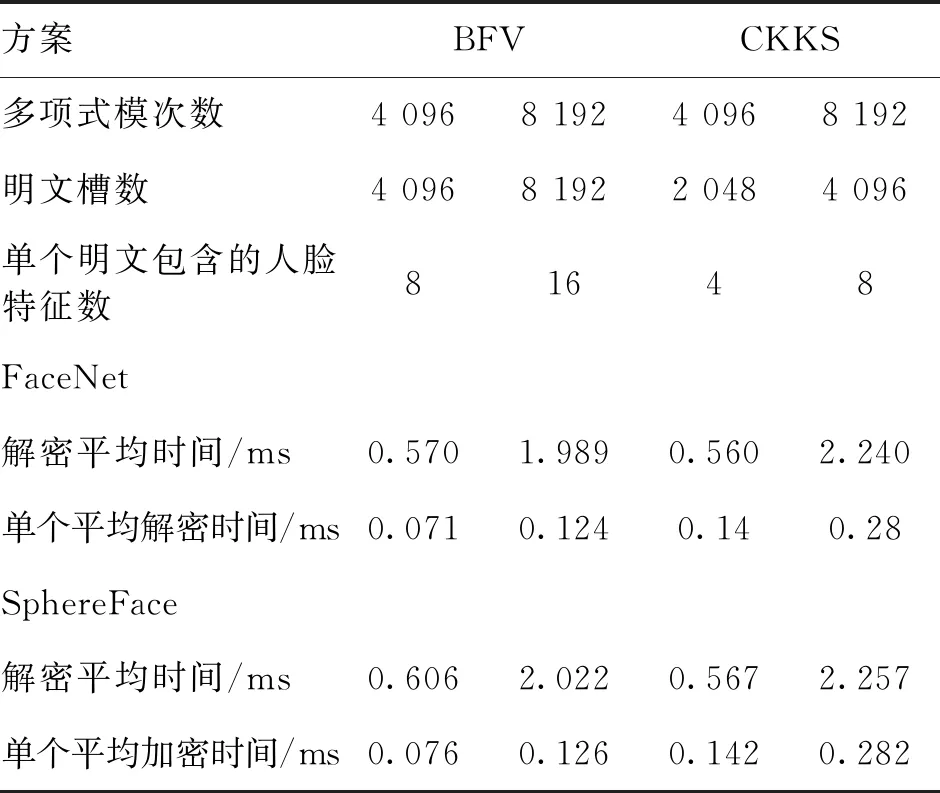
表5 解密时间统计
4.5 性能分析
综上,将一对人脸在全同态下的人脸识别的整体耗时与未加密的进行对比,如表6所示:
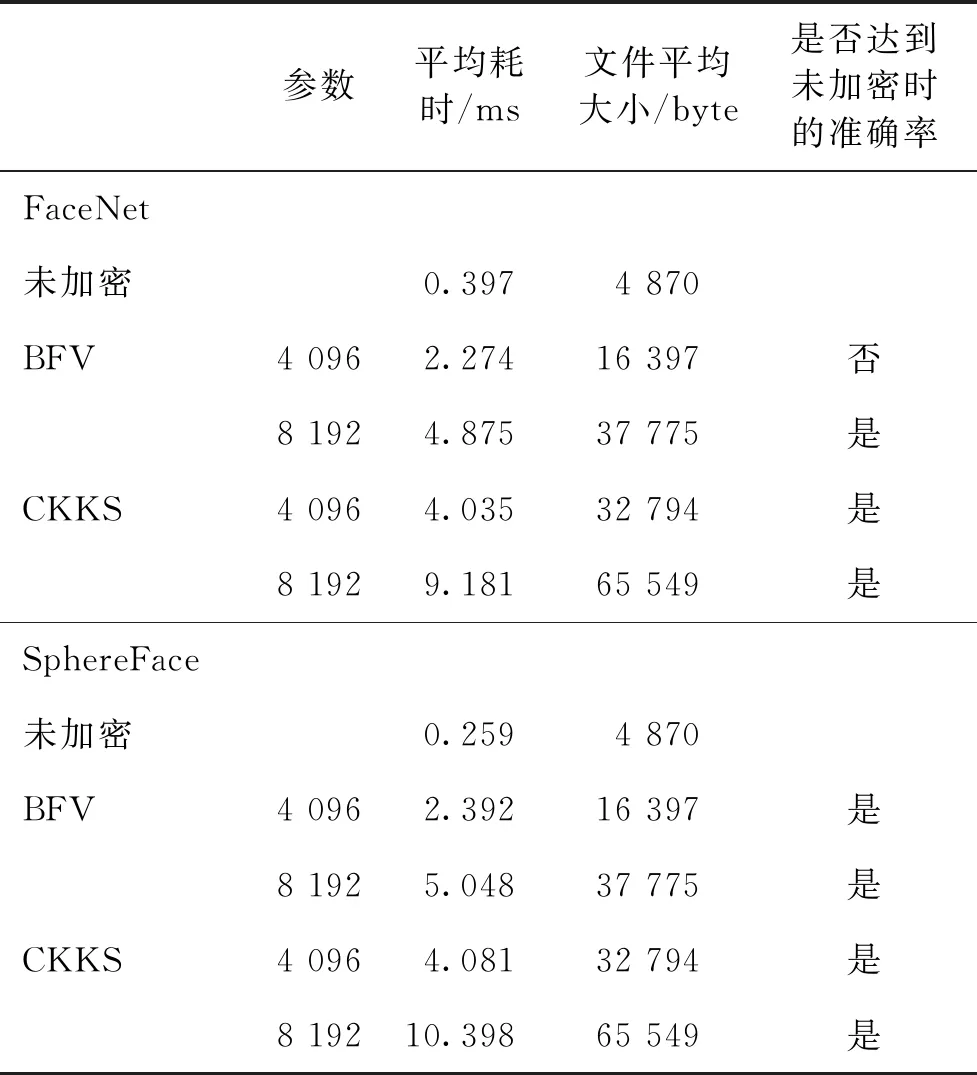
表6 未加密与加密情况下人脸识别整体用时
从表6可知,在FaceNet算法中,由于存在更多次的同态操作,导致噪声消耗更大。因此,在多项式模次数为4 096时无法达到未加密时的准确率,其他参数下都可以达到。
从其他各个参数下的平均耗时和文件平均大小对比,可给出建议:当对安全等级要求相对较低时,可选择支持浮点数的多项式模为4 096的CKKS方案,与未加密时的人脸识别相比,时间上增加了约3.6 ms,特征文件增加了27 924 byte(约27 K);安全等级要求相对较高时,可选择多项式模为8 192的BFV方案,与未加密时的人脸识别相比,时间上增加了约4.6 ms,特征文件增加了32 905 byte(约32 K);它们都能够保持未加密时的人脸识别准确率。
使用全同态对人脸特征进行加密,虽然计算时间和存储空间都相应增加了,但是增加的时间在整体人脸识别系统中(考虑摄像头采集人脸所花费的时间、注册和登录的过程图形界面载入和网络通信耗时)所占的比例大约为3%。因此,对人脸特征密文进行全同态计算的效率是能够满足实际应用需求的。
5 结束语
随着人脸识别的快速应用,个人信息保护在数字经济时代受到了空前的挑战。个人人脸隐私信息的安全保护已成为社会关注的重点。本文探讨了基于神经网络模型使用全同态加密来保护人脸特征的可行性,并在加密域中对人脸相似度计算进行优化,利用基于中国剩余定理的批处理技术,提高了在加密域中人脸匹配的效率。本文设计的隐私保护的高效人脸认证方案,既达到了保护用户人脸特征的安全目标,也保持了未加密时人脸识别算法的准确率,还能够满足实际应用的性能需求。
在互联网技术蓬勃发展的时代,保护个人信息不受侵犯,需要政府加强监管,严惩违法违规分子;也需要企业补齐技术短板,规范个人信息收集、储存、使用等过程。

