舰载直升机舰面共振非线性建模与分析

孙凤楠，朱艳，李贞坤

（中国直升机设计研究所直升机旋翼动力学重点实验室，江西景德镇，333001）

舰面共振是舰载直升机研制过程中必须考虑的一个动力学问题，处于海洋气象环境下的舰船在各级海况下停泊或航行都会产生摇晃。旋翼和机体系统的动力学特性在舰船振动环境中会发生显著变化，致使存在或可能出现由于旋翼与机体耦合运动产生的舰面共振不稳定现象，这是一个直接影响到机舰安全的动力学问题[1-3]。

国内外研究人员主要从理论分析和仿真计算两方面研究舰载直升机“舰面共振”动力学问题。针对此问题，William等[4]考虑海风和舰船滚转运动的影响建立了舰载直升机动力学模型。Han等[5]利用有限元方法模拟了旋翼桨叶并考虑舰船6个运动自由度，建立了描述舰载直升机和舰船耦合的动力学模型。Darren等[6]通过建立较为完整的起落架模型分析了舰载直升机在舰船甲板上的操纵动力学问题。刘洋和向锦武[7]考虑舰载直升机起落架系统的非线性特性，采用多体动力学方法建立了舰载直升机旋翼/机体耦合动力学模型，研究了不同舰船激励频率下舰载直升机启动过程中的动力学稳定性。周华[8]选取某两型舰船，对比分析了不同海情状况对舰载直升机“舰面共振”特性的影响，张然[9]建立了某型直升机的旋翼/机体/舰面耦合系统动力学分析模型，使用牛顿法推导了旋翼/机体/舰面耦合运动方程，采用状态空间法和频响函数法分析了某型直升机的“舰面共振”特性。赵则利[10]运用AMESim仿真平台研究了“舰面共振”对舰载直升机主起落架液压缓冲器的性能影响。

本文首先考虑舰船纵摇、横摇和沉浮运动以简谐激励的形式通过起落架传递至旋翼/机体耦合系统；其次对旋翼粘弹减摆器的刚度阻尼进行非线性动特性分析，考虑旋翼桨叶挥舞摆振运动和气动力的影响，将旋翼、机体作为子系统分别建模，根据力学原理将各子系统组装到整个分析模型中；最后，建立描述全机在舰面运动及舰船运动影响的舰载直升机舰面共振分析模型。根据舰面共振动力学方程的非线性特点，结合稳定性分析目标，采用四阶Runge-Kutta法分析旋翼/机体/舰面耦合系统在扰动下的瞬态响应，计算分析其稳定性，并揭示舰船运动、部件非线性动力学特性对稳定性的影响。本文的分析不仅可代替型号研制中无法进行的试验，更是为研制性能优良、安全性和可靠性高的先进舰载直升机提供了技术保证。

1 “舰面共振”理论建模

本部分将机体、起落架和旋翼系统作为子系统分别建模，综合各子系统的动力学特性，充分考虑旋翼减摆器刚度和阻尼的非线性特性随海况和舰船振动环境的变化，考虑旋翼桨叶挥舞摆振运动及气动力影响，建立了描述全机在舰面运动及舰船运动影响的舰载直升机着舰旋翼/机体/起落架/舰面系统动力学模型。

■1.1 机体模型

假设机体为刚体，起落架对机体提供弹性约束和阻尼，考虑机体在空间的6个刚体运动自由度，X、Y、Z、ΦX、ΦY、ΦZ(航向、侧向和垂向的位移，及横滚、俯仰和偏航运动)，建立机体模型。

图1 机体模型

机体模型如图1所示。机体坐标系原点位于机体重心处，X轴为航向，向后为正；Y轴为侧向，向右为正；Z轴为垂向，向上为正，桨盘前倾角为零。模型中定义了起落架安装于机体的几何参数及桨毂中心到机体重心的几何参数，根据某型机的全机构型，起落架采用前三点立柱式布局，其刚度阻尼针对通用型起落架给出。本文采用空间动力模型，将整个动力系统分为机身系统和旋翼系统两部分。

■1.2 起落架模型

舰载直升机在舰面甲板上起降时，舰船沉浮、横摇和纵摇运动使得舰船会对起落架系统产生一个垂向的作用力，作用点为起落架机轮在舰面上的着陆点。对于主起落架和前起落架，单个起落架的受载形式都是一样的。自由系留状态起落架的垂向受力情况如图2所示，图中起落架受到舰面对其的载荷P，设缓冲器的压缩位移为S，机轮的压缩位移为ZT,单个起落架垂向压缩总位移为Z=S+ZT，根据舰船运动随海况的变化其左右主起机轮、缓冲器的压缩量Z均不相同。

当直升机在舰面甲板上起降时，单个机轮运动如图3所示。

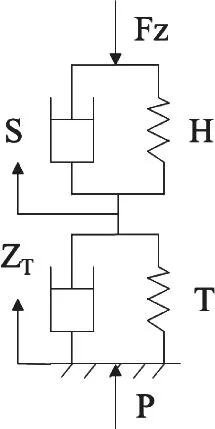
图2 单个起落架垂向受力平衡

图3 单个机轮运动示意图

图3中ZJ表示舰的运动，FS是缓冲器作用于机轮的轴向力，MT是机轮质量，K和C是机轮的垂向刚度和阻尼，本文中所需的缓冲器轴向力和机轮刚度阻尼力均通过试验数据插值获得，对于该机轮，其运动方程（不考虑舰运动引起的机轮阻尼项）为：

平衡计算时，三个着舰点处的运动位移ZJ各不相同，ZJ可表示为： ZJ=ZJ0sinωJt ，ZJ0为着舰点沉浮初始幅值，ωJ为舰船沉浮频率。同理，机轮着舰点还有舰的航向和侧向运动，分别假设为： XJ=XJ0sinωXt 和YJ=YJ0sinωYt，舰的运动使机轮航向和侧向受到的激励力分别为：

式中，XJ0为横摇初始幅值，Xω为横摇频率，YJ0为纵摇初始幅值，Yω为纵瑶频率。Kx、Ky为机轮航向、侧向刚度。

■1.3 旋翼桨叶模型

旋翼系统桨叶模型如图4所示，图中描述了桨叶绕挥舞铰挥舞kβ运动，桨叶绕垂直铰摆振kζ运动，（k=1，2…Nb片桨叶），桨毂坐标{0，0，Zh},第k片桨叶随桨毂一起旋转Ωt转角，绕垂直铰摆动ζk。一片桨叶的质量定义为mb，绕垂直铰摆动的质量静矩定义为Sb以及绕垂直铰摆动的质量惯性矩定义为Ib。

图4 旋翼系统桨叶挥舞摆振运动模型

结合型号减摆器静压缩载荷数据和动态刚度阻尼数据，构造了旋翼减摆器非线性动力学模型，通过最小二乘法拟合公式中的待定系数，并通过相关试验数据进行校核和修正，最终确定系数得到旋翼减摆器非线性动力学模型。

粘弹减摆器载荷与位移的解析式设计为：

其中，s是压缩位移，ks0、ks1、ks2、ks3、ks4、cd0、cd1、cd2、cd3、cd4为待定系数，G (s)、 G (s)为粘弹减摆器刚度和阻尼。

图5为根据粘弹减摆器刚度试验数据，采用最小二乘法拟合获得粘弹减摆器刚度与振幅的关系，表达式如下：

图5 粘弹减摆器无量纲拟合刚度曲线

同理，图6为无量纲阻尼试验数据拟合曲线，得出粘弹减摆器阻尼与振幅关系式：

图6 粘弹减摆器无量纲拟合阻尼曲线

■1.4 桨叶气动力模型

图7给出了桨叶翼型剖面上的气动力。

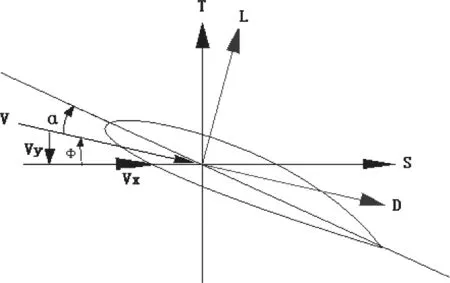
图7 桨叶剖面气动力模型

根据桨叶运动在其剖面上产生的气动载荷，确定桨叶沿展向r处剖面上的气动力素，最终可推导得桨叶升力向气动载荷Tk、桨叶摆振向气动载荷、桨叶绕垂直铰的摆振气动力矩，及作用于桨毂的航向气动力、侧向气动力、升力向气动力、俯仰滚转偏航气动力矩，及周期变距产生的气动载荷。

旋翼气动力模型采用准定常气动力和均匀入流模型，其详细推导见参考文献[11]，此处不作详细叙述。

■1.5 转速方程

为模拟开车过程中转速的变化，引入包括旋翼、主减速器、发动机和传动系统整个动力传动链的扭转运动方程，动态仿真直升机模拟启动开车到地慢和额定转速，这需要转速方程控制，并且舰面共振方程输出项中含旋翼扭矩负载，其影响转速方程，也是方程的外激载荷。从而建立传动系统的扭振运动和旋翼摆振与机体的运动耦合关系。设旋翼集合型摆振惯性矩为I0，转速方程为：

这里，ME是发动机燃气涡轮作用于动力涡轮的驱动扭矩，MK是旋翼的反扭矩，也就是作用于桨毂的偏航气动力矩，它与转速、诱导速度有关。

■1.6 模型组装

结合单个起落架的平衡方程，联立旋翼/机体耦合的力和力矩平衡方程与桨叶运动摆振方程、挥舞运动方程联立，可得舰面共振非线性方程，简写成下列微分方程矩阵形式：

其中，

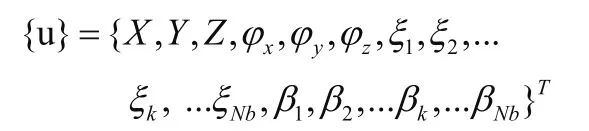
其包含6+2Nb个元素的向量，[M]、 [C]、 [K]为非线性系数矩阵。

系数矩阵的元素是非线性的，采用数值积分方法，通过计算初始条件下、或扰动条件下的响应，分析其稳定性。

2 计算方法

将方程（7）变换后组成如下矩阵形式，得：

将方程（8）降阶为一阶方程形式：

采用4 阶龙格库塔法求解方程，首先置所有变量初值为0，因为直升机由静止状态开启发动机，带动旋翼转动，随着旋翼转动，气动载荷增大，旋翼桨叶和机体都在气动载荷作用下振动起来，通过龙格库塔法计算这一过程旋翼桨叶、机体和起落架机轮的运动响应。方程右端的作用力项中，包括了舰的运动ZJ，它是低频的基础激励，还包括与旋翼、机体运动相关的气动载荷。由于动力耦合系统的固有频率低，时间积分步长取0.01s即可满足计算收敛要求。

数值求解方程过程中，将输出桨叶、机体的运动随时间的变化历程，即输出每个机体运动自由度和桨叶运动的速度、位移。通过绘制响应历程可观察到动力系统在该状态下的运动状态和稳定性。

旋翼转速加速和总距提距过程中，都由于施加了激励，同样会激起动力系统的瞬态响应。实际的直升机开车和提距或加速过程，都会产生较大的瞬态响应，本动力学方程可描述这一现象，从这一过程也可看出动力系统在瞬态激励状态下的稳定性。

3 结果与讨论

本文所用模型直升机无量纲参数如表1所示，旋翼采用铰接式构型，机体起落架系统的缓冲器和机轮刚度阻尼通过试验数据插值获得，计算过程中通过插值方法获得对应状态的频率和阻尼值。

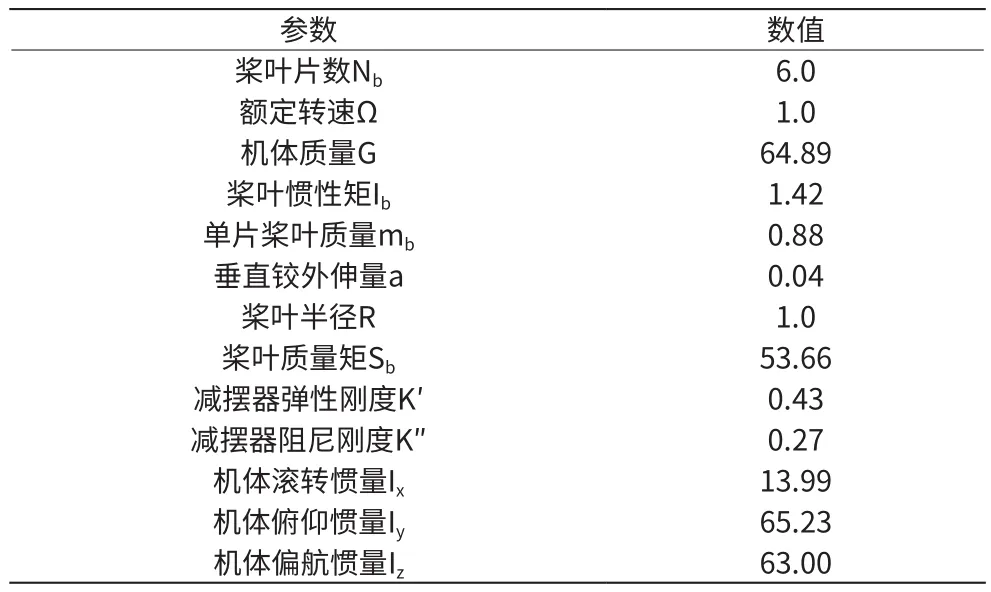
表1 直升机无量纲参数

直升机在舰面更关心的是受到长时间激励下的稳定性，实际状态下激励是随机瞬态激励，即间断性的瞬态激励。为了模拟长时间的激励，采用稳态正弦激励，稳态正弦激励的激励频率选取为旋翼摆振后退频率，这是检查舰面共振最有效的方法，它模拟了可能发生不稳定性的最危险状态，所称极端状态。如果在这种极端状态下动力系统是稳定的，那么在其它任何状态下都是稳定的。

以某型机最大起飞重量G为例，通过模拟两次提总距，旋翼从0时刻零转速加速到慢车，在地慢运转60s时刻后加速到空慢额定转速，并且转速稳定在地慢和空慢额定转速时施加激振，在地慢55s时刻及额定转速运转90s时刻下施加激振力，激励时长1s。

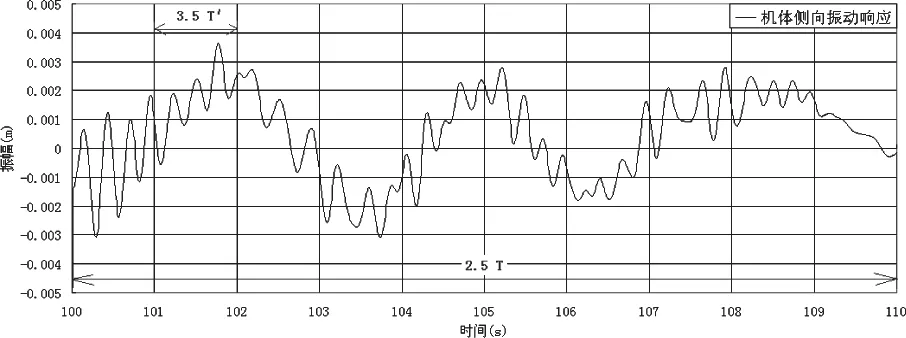
图8 机体侧向振动响应时间历程（自由着舰，舰船横摇）（时间100s-110s）

由图8可以看出仿真试验自由着舰下全机振动由机身低频运动和起落架高频振动叠加而成，仿真试验能描绘真实舰载直升机舰面开车情况。

图9 机体侧向振动响应时间历程（自由着舰，舰船横摇）

图10 桨叶响应时间历程（自由着舰，舰船横摇）

图11 机体侧向振动响应时间历程（自由着舰，舰船横摇）

图9～图12为自由着舰时舰面共振稳定性分析计算结果，仿真直升机在舰船上开车从旋翼零速度到慢车再到额定转速的全过程，模拟舰的摇晃运动（横摇、纵摇）对机体产生激励载荷，模拟两次提总距，模拟扰动驾驶杆周期激励，在慢车下55s时刻和额定转速下90s时刻施加激励，仿真计算机体响应和桨叶摆振运动。

当取舰船横摇振幅为6°，纵摇振幅为3°，从图9～图12可看出，自由着舰时舰面开车机体在舰船摇晃随机瞬态激励的作用下，激起机体侧向振动响应及桨叶摆振响应的增大，当停止激振后，响应有所减弱，总体来看振幅没有出现发散现象，说明机体振动在工作转速范围内是稳定的（不发散），即不会出现舰面共振不稳定性现象。结合该型机舰面共振线性计算结果，表明非线性分析方法的正确性，并且线性计算结果更偏于保守。此外，从图9～图12可看出仿真曲线的波动变化较大，这一现象正好体现出部件非线性动特性对舰载直升机稳定性的影响，由于舰面共振是在频率单一外激励下的受迫振动，因此本文不考虑粘弹减摆器双频特性对其的影响。

4 结论

本文建立了描述舰载直升机自由着舰的舰面共振非线性动力学模型，考虑了旋翼系统粘弹减摆器及起落架系统的非线性特性，模拟舰船的摇晃运动对机体产生激励载荷，基于四阶Runge-Kutta法，采用数字仿真技术动态演示舰载直升机舰面共振开车试验过程，仿真舰载直升机舰面上开车从旋翼零转速到地慢转速再到额定转速的全过程，真实模拟提总距及通过扰动驾驶杆进行周期激励，得出结论如下：

（1）仿真计算自由着舰舰面开车，机体在舰船摇晃随机瞬态激励的作用下，机体振动在工作转速范围内是稳定的（不发散），不会发生舰面共振。

（2）仿真试验结果显示全机振动由机身低频运动和起落架高频振动叠加而成，仿真试验能描绘真实直升机舰面开车情况。

（3）仿真曲线的波动较大，体现出部件非线性动特性对直升机稳定性的影响。