图形的旋转变换在初中平面几何中的运用探讨
刘志敏
【摘要】图形变换在初中数学几何教学中经常遇到,在一些特殊图形变换——图形旋转类的试题往往是很多学生头疼的地方。文章基于几种图形旋转试题的教学经验,探讨如何在这几类试题中寻找解决问题的关键点,在解题分析中梳理逻辑思路,从而有效提高这类问题的教学质量。
【关键词】初中数学;平面几何;图形的旋转;教学探讨
一般而言,初中几何课程中的图形变换涵盖平移、轴对称、旋转,是对图形运动变化规则的论述,尤其图形旋转重中之重。在历年的中考试题中,这类题目考查往往是重分,常受到命题者的青睐,考查的知识点又多又杂。因为这类试题涉及三角形、四边形、圆等初中数学几何的重要图形内容,里面考查的知识点往往很复杂、综合性、逻辑性很强。在初中毕业班考试中,这类试题是各类考试中常见试题之一。教师需要结合具体图形需要寻找策略,只改变图形位置这一特性,把分散的元素集中起来,充分利用题中各元素最终使问题简单化,最终形成求解几何题的依据、思维方向。文章就图形旋转法在以下几种问题中的应用举例说明。
一、在求三角形角度问题中的应用
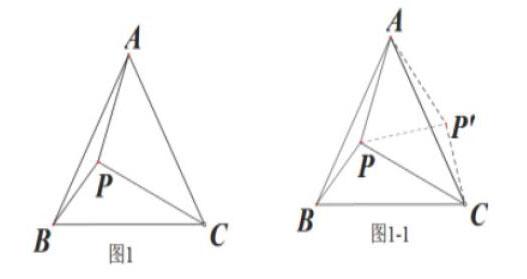
教师需要抓住题目要求,分析题目条件,选择合适的旋转点,从而构造性的图形,再将新的图形与原来的条件对应,从而找到问题的破口。其实很多这类问题都是如此,没有找到突破口将不会解决问题。下面一道三角形角度问题而言,教师需要在试题中分析问题的关键点,即突破口才能迎刃而解。诸如,如图1,在△ABC中,AB=AC,∠BAC=60。,AP=4,BP=3,CP=5,求∠APB的度数。
在阅读题目后,教师引导学生这样分析题目:由于条件中的AP=4,BP=3,CP=5像是勾股数,但又比较分散,不在同一个三角形中无法有效利用,于是想到利用图形的旋转方式改变图形位置但不改变形状大小这一性质,把分散的元素集中起来。在这道试题中,我们需要找到必要的关系量。因为等边△ABC中有共顶点等线段AB和AC,所以在旋转过程中,以点A为旋转中心,将△ABP逆时针旋转60°到△ACP'位置,连接PP‘(如图1-1)得到△APP'是等边三角形,通过转移把已知条件中的AP=4,BP=3,CP=5集中到了△PP'C中,再结合勾股定理逆定理得到∠PP'C=90。,又由∠APB=∠AP'C=∠AP'P+∠PP'C=60。+90。=150。。
二、在求线段的长度问题中的应用
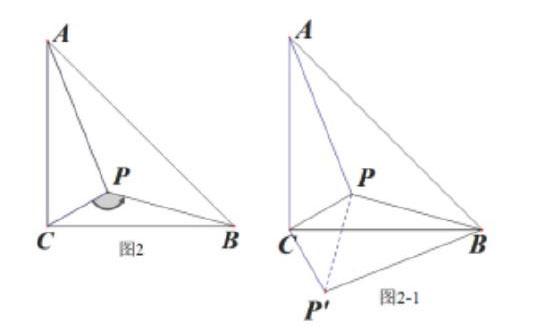
梳理题目条件与要求,转化问题,适当将线段长度问题分散的条件集中在一起,对图形合适旋转即可。这类问题在求线段的长度问题方面,教师需要引导学生将分散的条件进行巧妙地集中。诸如,如图2,在Rt△ACB中,CA=CB,点P为Rt△ACB内一点。已知AP=10,BP=8,且∠CPB=135。,求CP的长。
在阅读题目后,教师引导学生这样分析题目:由于题中各元素条件比较分散,不将其集中起来,直接求CP的长度不好完成求解任务,是否可以考虑将分散的元素集中起来?条件中有共顶点等线段CB和CA,于是以C为旋转中心,将△ACP逆时针旋转90°到△BCP位置,连接PP(如图2-1)得到等腰直角△PCP并且把AP=10,BP=8,转移到了中△BPP。由旋转性质得到等腰直角△PCP中∠CPP=45。和∠BPP=90。,再根据勾股定理可以求得PP的长度,于是在等腰直角△PCP中直角边PC的长度就迎刃而解了。
三、求线段的和差关系
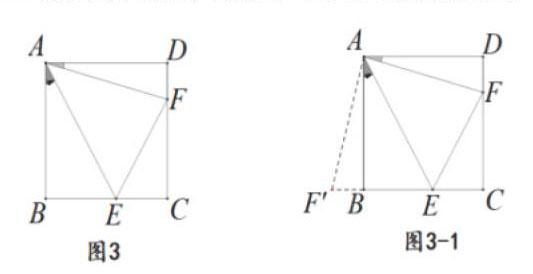
在求解复杂几何题时,教师需要引导学生有效地进行图形变换,将分散的已知条件集中起来,构成新的基本图形,创造有利条件,综合分析,破题解题。在关于线段和差问题中,一般要看能否将图形旋转到某处,看看是否能共线,这样就能将问题得以解决。例如,如图3,在正方形ABCD中,点E与点F分别为BC、CD上动点,且∠FAE=45。,请根据条件分析线段BE、DF、EF存在什么样的关系,并说明理由。
在阅读题目后,教师引导学生这样分析题目:线段BE、DF、EF的关系为DF+BE=EF。要证明两条线段之和等于某线段,即可以考虑用“截长补短法”求解。不过,在这道题目中,显然又难以实现这种做法,必然导致由于这题中条件不足截长法不易证得。其实,题中条件正方形ABCD中含有共顶点等线段AB和AD,为此,不妨将以A点作为旋转点,将Rt△ADF以顺时针旋转90°到Rt△ABF'位置(如图3-1)。由旋转的性质得∠F'BE=180。,即点F'、B、E三点共线。接着,再证EF'=EF即可得证原问题。
四、在求图形面积问题中的应用
在涉及图形面积上,显然不是直接要求问题最后图形的面积,是将问题转化成同已知条件相符的特殊图形,这就是一种转换思想。当然,部分题目还需要两个旋转图形,才能使问题得以解决。例如,如图4,点P为正方形ABCD内一点,由点P到其中三个顶点的距离分别为PA=1,PB=2,PC=3,请问正方形ABCD的面积是多少。
在阅读题目后,教师引导学生这样分析题目:此题已知为PA=1,PB=2,PC=3,要求正方形ABCD的面积,刚看真的有点风马牛不相及无从下手,但考虑到正方形中不乏有共顶点等线段的条件,肯定要想着一些等量替换的做法。不妨将△ABP点A逆时针旋转90°得到△ADP',将△BCP绕点C顺时针旋转90°得到△DCP'',再分别连接PP',PP''得到等腰直角△APP'和△CPP'(如图4-1),由旋转性质易得∠P'DP''=180。,即P'、D、P''三点共线。通过计算PP'、PP''、P'P''三边长并根据勾股定理逆定理可以得到△PP'P''也是直角三角形。从而可以得到正方形ABCD的面积等于Rt△AP'P''、Rt△PP'P'',Rt△PCP''的面積之和。
另外,针对一些复杂图形,即两种或两种以上图形的情况,要懂得图形与图形之间的关系,在特殊关系中寻求问题的突破口。诸如,圆与三角形、圆与四边形等都需要特殊考虑,因为两种图形结合的考查的知识点更多,需要的综合性思维更加强。例如,如图5,等边△ABC内接于圆O,点P是劣弧BC上一点,PA=2,求四边形ABPC的面积。
在阅读题目后,教师引导学生这样分析题目:题中条件只给出一条线段长度,要求四边形ABPC的的面积,直接求很难找到突破口。由于题中条件给的是等边三角形,存在等线段共顶点的线段,于是可以尝试用旋转法解题。现将△APC绕点B逆时针旋转60°让AC=AB与重合(如图5-1),得到△AP'B。由旋转的性质易得∠P'BP=180。∠P',即点P',B,P三点共线,通过旋转将求四边形ABPC的面积转化为求△APP'的面积。而△APP'是等边三角形且边长PA=2,所以△APP'的面积不难求得。
综上所述, 很多时候,学生会感觉几何证明题存在困难,要么是难以综合现有条件寻找解题方法,要么是辅助线添加存在问题……其主要根源在于学生对图形的性质、判定不够,因而导致对几何知识的恐惧。文章通过以上几种题型分析可以看出, 旋转变换对解决平面几何中的某些问题举足轻重, 特别是在解决有关等边三角形、等腰直角三角形、正方形、圆形等问题时, 更是经常用到它。当然,教师在平时教学中,要引导学生做题时的思维退出课本要求,要懂得几何知识的学以致用,以知为谋,将知识转化为技能,破题解题。只要在平时的学习中多加研究, 就可以让平面几何中的某些问题迎刃而解, 起到事半功倍的作用。
参考文献:
[1]邓厚波.深度对话·相机追问:让数学课更显几何味——李庾南老师“图形的旋转”课例赏析[J].中学数学(初中版),2020(6):33.
[2]马娇,孙晓峰.图形旋转之妙用[J].初中生世界,2020(5):47-48.

