在数学学习过程中学会思考
贲友林
“找规律”教学,既要重视找规律的结果,也要重视找规律的过程。找规律,经历思考、交流、探索的过程,体验发现规律的方法,积累在解决问题的过程中发现规律的经验,发展归纳与概括的能力。
一、交流:我是怎样想的
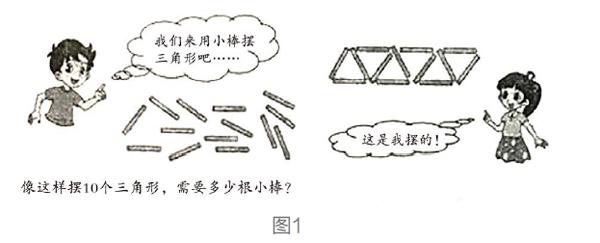
师:(屏幕上出示空白的“研究学习”材料)课前,大家做过这份材料(如图1),请同桌之间先交流一下自己的想法。
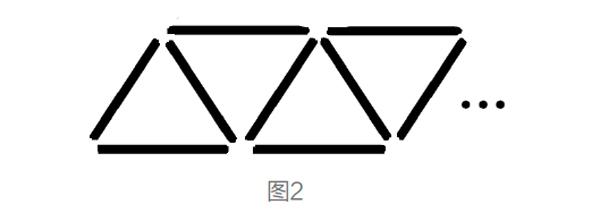
师:张睿嘉,能讲吗?好像不太自信,大家掌声鼓励一下!(全班鼓掌)我想给张睿嘉一个挑战—请到黑板这边来讲,这样大家看得见。题目中是摆小棒,我们可以画图(如图2)。
师:接着画下去,有规律,第10个三角形是向上还是向下?(教师让张睿嘉请班上同学回答)
阎馨宁:向上的。
花飞燕:我觉得是向下的。
毕明远:我也觉得是向下的。因为向上的都是奇数,而10是偶数,所以是向下的。
师:我特别欣赏刚才第3位同学的发言,在前两个同学发言之后,他表达了自己的想法,更关键的是,他解释了为什么向下。这样的发言要不要有掌声?(全班鼓掌)第10个三角形,究竟是向上还是向下?
生:我觉得应该向下。因为我发现,1、3、5这些三角形都是朝上的,2、4、6都是朝下的,所以我觉得10是偶数,是朝下的。
师:思路很清晰,把刚刚同学的想法说得更清楚了。来,我们一起看1、3、5这些奇数的三角形都是怎样的。
生:向上。
生:2、4、6都是向下。
师:第10个,也就是最后一个呢?
生:向下。(教师画第10个三角形)
师:那第9个呢?
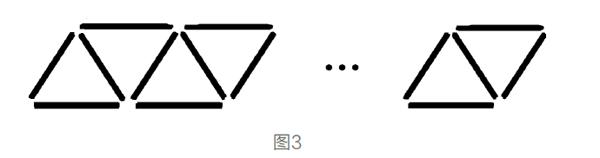
生:向上。(教师画第9个三角形,如图3)
师:画好了以后,张睿嘉要来讲讲他是怎么想的。我给个建议,最好先圈圈画画,然后再讲。
张睿嘉:我觉得10-1=9(个),9×2=18(根)。
(教师打断张睿嘉讲解,提醒:稍等,哪儿是10,指着图说)10-1=9(个),9×2=18(根),18+3=21(根)。大家有疑问或补充吗?
师:比刚才更快了。慢慢来,哪儿是10?
张睿嘉:我觉得先用10-1=9,(教师再次打断,再次提醒:一步一步来,先讲讲10表示什么)10表示—(停顿了约有10秒时间)10表示10个三角形。
师:(示意张睿嘉暂停,转而问全班)慢一点。刚刚他说10表示什么?
生:(齐)10个三角形。
师:说得怎么样?(全班鼓掌。教师指着图)10表示这里有10个三角形,那减1呢?
张睿嘉:10-1=9……(教师打断,提醒:慢一点,1表示什么)1是1个三角形。
师:1是哪一个三角形?你把这个三角形圈起来。
(张睿嘉把图中的第9个三角形圈起来)
张睿嘉:10-1=9(个),9×2=18(根)。
师:继续,9×2。9是9个三角形,2呢?
张睿嘉:2是这两个三角形。
师:2表示这两个三角形,那9×2呢?(张睿嘉沉默)
师:(提示)你可以继续思考,也可以选择举手的同学回答问题。
(张睿嘉点名江咏岳回答问题)
江咏岳:10个三角形,先把最边上的那一个圈出来,就是把最左边的三角形圈起来。可以看出这个三角形是用3根小棒拼出来的,后面的三角形只用了2根小棒就拼出了。
师:(对着张睿嘉)现在你重新来圈,一边圈一边讲。第1个三角形怎么样?
张睿嘉:(圈起左边第1个三角形)第1个是3根小棒。(指着左边第1个三角形的3根小棒)21减去这3根小棒等于18根。
师:看来刚刚同学讲的,你还没有完全听懂。没关系,继续听同学讲解。
(张睿嘉点名邀请肖翊讲解)
肖翊:我觉得最后一个三角形,不能圈3根,只能圈2根,不然倒数第2个三角形,就只有1根了,因为倒数第2个三角形靠左的那條边被前一个三角形占用了,所以最后一个三角形只能画两条边,不能画3条边。
师:好了,我们一起来解释算式,第1个算式10-1=9表示什么?
张睿嘉:10表示10个三角形,减掉1个三角形,等于9个三角形。
师:减去哪个三角形?
(张睿嘉指左边第1个三角形)
师:为什么要把这个三角形减掉?
张睿嘉:因为它有3根小棒。
师:后面的三角形,我们也圈一下。换一种颜色的粉笔,第1个三角形已经圈了,把后面的三角形圈起来。
师:画完以后,我们再看一下,一共是几个三角形?
生:10个。
师:第1个三角形呢?
生:3根小棒。
师:后面还有几个三角形?
张睿嘉:9个。
师:这些三角形怎么样?
张睿嘉:都是两根小棒。
师:(指着后面的三角形)那这一共有多少个2呢?
张睿嘉:9个2。
师:马上想到一个乘法算式。
张睿嘉:2×9=18。(板书:2×9)
师:我们列综合算式。
张睿嘉:加上3。(板书:+3。如图4)
【分析】教师先通过听课教师抽报学号的方式邀请一位学生与全班交流。抽签,是让每位学生意识到他们每个人都有想法,都可以也应该与全班交流。
张睿嘉和全班同学的解释与交流,用了一节课的近一半时间。教师对一位学生,为何如此?第一,学习思考,“一个都不能少”。第二,语言是思维的外壳。教师要让学生不仅做出来,而且还能说出来。因为只有想明白了,才能说清楚。第三,如果后续学习过程中学生会圈圈画画讲解,这段教学就是有价值的。由此看来,这不是面对一个人的教学,而是全班在一起思考,共同学习。
师:这是张睿嘉的想法,再看看你做的和他一样吗?一样的,不说了;不一样的,赶紧举手。
(张睿嘉邀请罗皓仁和全班交流)
罗皓仁:我的想法是这样的,这边有10个三角形,第1个三角形由3根小棒组成,其他9个都是由2根小棒组成,我现在把第1个三角形也看成由2根小棒组成的,就是2×10=20。20再加上刚才去掉的1根小棒,20+1=21。(全班鼓掌)
师:刚刚他说的算式,听到了吗?是什么?
生:2×10+1=21。
师:如果看这个算式,在图上圈,怎样圈呢?
罗皓仁:第1根小棒不算,把第1个三角形看作由两根小棒组成的,其他三角形都是由两根小棒组成的,就是10×2。再加第1根(如图5)。
庆雨宸:我的这种方法,可能不太好解释。但是可以这样看,(教师在黑板上画好小棒摆成的三角形图,让庆雨宸在黑板上圈画讲解)刚才罗皓仁用的方法,相当于不看第1根小棒,我还有一种方法,是补充1根小棒。(庆雨宸在左边第1个三角形左边画了1根小棒)这里的1根小棒可以和原来左边1根小根拼成两根,一共相当于有11个两根小棒,(板书:11×2)一开始这1根小棒不是真实存在的,所以要减去。(板书:-1。如图6)
师:这个方法和前面的一样,还是不一样?
生:不一样。(全班鼓掌)
师:假设有这根小棒,那就有多少呢?
生:(齐)11个2。
庆雨宸:我认为罗皓仁这里也应用了假设法。(指着罗皓仁所圈画的最左边的1根小棒)假设这根小棒不存在。大家还有什么疑问吗?
师:太厉害了!庆雨宸不仅讲清楚了自己的想法,可以假设这里增加1根,他还想到,既然可以增加1根,也可以怎么样?
生:假设减少1根。
师:(指着罗皓仁圈画的图5)这不就是假设减少1根吗?掌声再次送给庆雨宸。听这样的发言,太享受了。现在发现这个问题,我们有多少种方法?
生:3种。
师:(在之前圈画的图前面标注序号①②③)尤其表扬庆雨宸,他发现第2种想法跟第3种想法有联系。有什么样的联系?
生:都用了假设。
师:假设多1根,或者少1根。你们想到了3种方法,还有没有第4种方法?(部分学生举手,庆雨宸邀请喻高进和大家交流)
喻高进:刚才庆雨宸、罗皓仁想的都是两根小棒为一组,我也可以假设3根小棒为一组。把后面9个三角形都补画1根小棒,然后把每3根小棒组成的三角形圈画出来。这时,10个三角形都是独立的三角形,独立的三角形是3根小棒(如图7)。
生:我觉得现在的图和以前的图比,除了第1个三角形是由3根小棒组成的,后面2根小棒组成的三角形都加了1根小棒,变成了独立的三角形。
师:就是说,第1个三角形是3根小棒,后面的三角形都要怎么样?
生:都加1根小棒。
师:每个三角形再加1根小棒,这样一共加了几根小棒?
生:后面9个三角形,要加9根小棒。
教:那个9,要怎样?
生:减掉。
师:(对着喻高进)这种想法,你之前是没想到,对吗?
喻高进:我之前没想到。后来看了罗皓仁、庆雨宸的想法后我想到的。
师:学习就是这样,别人的想法会让我有新的思考、新的想法。
【分析】课堂是一群人在一起学习,是发生在群体中“他人在场”的学习。当一个班级的学生在一起的时候,每位学生都带来了各自的想法,教师要做的是,组织学生展示、交流各自的想法。
课堂中的学习与思考,不仅仅“向外”,与同学、教师分享自己的想法;还要“向内”,在“说”与“听”的过程中,促使自己生成新的想法,促使自己对学习内容的认识经历“原来我是怎样想、怎样做”“还可以这样想、这样做”“现在我是这样想、这样做”的过程。这樣,思维从平衡到失衡,再形成新的平衡,从而深度构建对学习内容的理解。
二、探讨:让他也能做出来
师:这道题目,你可能有想法1、想法2、想法3,甚至想法4,可是有同学却没有做出来。我们要想一个办法,让他也能做出来,做正确。
生:我觉得可以发明一个公式,我就写了一个。几个三角形,把它设为n,(n-1)×2+3,这是我的想法。
师:有公式就简单了。可是,谁发明公式呢?有的同学发明不了啊。
生:我们还可以列表格、找规律,这样慢慢地就做出来了。例如,第1个三角形3根小棒,第2个三角形2根小棒……
师:刚才她讲的方法是什么?
生:列表格。
师:如果就这样画下去,画了10个三角形,能不能数出小棒的根数?
生:(齐)能。
师:画、数,是不是一种方法?
生:(齐)是。
师:只不过这种方法怎么样?
生:太麻烦了。
生:太慢了。
师:不过,答案是能找到的。刚才有同学说,列表,画着画着,表格出来了。
生:答案就出来了。
生:规律也出来了。
师:有发现吗?
王宇睿:第1个三角形的小棒根数是3,然后越来越多,小棒的根数每次都是往上涨2根的。
王思捷:我还发现,小棒的根数总是等于三角形的个数乘2加1。
生:我觉得刚才王宇睿的发现和王思捷的想法有联系。(学生跑到视频展台前,用红笔指着比画,并标注“+1”“+2”,如图8)三角形个数每次增加1,三角形个数和小棒根数之间的关系是乘2加1,三角形是加1的关系,1乘2等于2,小棒这儿就是加2的关系,所以“小棒根数依次加2”的规律是成立的。
注:图中的箭头与算式等,是教学中陆续添画的。
师:从上往下看,三角形的个数依次加1,小棒的根数依次加2。他解释了为什么三角形个数依次加1,小棒的根数依次加2。他发现三角形个数乘2加1,得到小棒根数。学习数学就要这样,刚才,联系起来思考;现在,深入思考为什么,想一想道理。回头想想,刚才男生(指王宇睿)说,小棒的根数依次加2,他是怎样看的?
生:竖着看。
师:竖着看,有规律。后面的女孩(指王思捷)是怎样看的?
生:横着看的。
师:第3位同学把竖着看、横着看联系起来思考,又有新的发现。为什么他们有发现?他们的观察是,可以竖着看,可以横着看,还要学会联系起来看。这样接着想,5个三角形,多少根小棒?
生:5×2+1=11(根)。
生:或者直接9加2就行。
师:接着想,10个三角形呢?
生:乘2加1。
师:100个三角形呢?
生:乘2加1。
师:当你发现这里的规律之后,这些问题就都很简单。
【分析】教师列表格的过程中,画画数数,贴近学生,又引领学生,藏巧于拙,化繁为简,以屈为伸。学生经历观察、思考、归纳、概括的过程,感受从简单情况想起的思维方法。
学生比较、寻找不同解法之间的联系。一是列表发现的规律与黑板上呈现的解法之间的联系,二是王宇睿与王思捷想法之间的联系,解释了“三角形个数增加1,小棒根数增加2”这一规律背后的道理。既有横向的联系,又有纵向的深入。学生将不同的想法关联起来,才可能走出狭隘与偏见,让自己的思维变得开阔。
三、拓展:我们看他问了什么问题
师:今天有两位同学没有来上课,我还是要展示一下他们的材料。(展台呈现27号周映宇的“研究学习”材料)我们看他问了什么问题?
生:(齐)像这样摆100个三角形需要几根小棒?
(展台呈现31号刘文林的“研究学习”材料)
生:(齊)用41根小棒可以摆几个这样的三角形?
生:前面的问题,是“乘2加1”;后面的问题,是倒着来的。
生:第1个问题,是告诉我们三角形个数,求小棒根数;第2个问题,是告诉我们小棒根数,求三角形个数。
师:问问题的角度不一样。倒过来怎样算,大家可以再思考。大家的想法很多。材料后面要求编题目,同学们编的问题都是摆什么图形?
生:正方形。
师:是的,很多同学都是编的正方形的题目。一定是正方形吗?
生:(七嘴八舌)五边形、六边形、长方形、平行四边形……
师:虽然要下课了,我还是展示一下我们班一位同学特别好玩的想法。有请9号孙鹤允。
孙鹤允:(跑到黑板上画图,如图9)我想这样摆小棒。
师:你能看出来不一样在哪儿吗?
生:她摆的是一个大三角形。
师:你们都是从左往右摆正方形、长方形,她把三角形怎么样?
生:摞起来了。
师:这里有没有规律呢?下课后可以继续探讨。
【分析】在数学学习过程中,学生想法比较单一时,教师要引导学生发散思维。不过,当学生的想法从“一”走向“多”之后,教师又要进一步引导学生集中思考,让想法从“多”走向“一”,促使学生的想法在广度、深度两方面和谐共进。
“找规律”这节课,教师在学生独立思考的基础上,先让学生把各自的想法呈现出来,借助学生不同的想法启发更多的学生打开思维。在交流过程中,让学生实时明晓他人的想法,知晓自己的想法,监控自己的认识:我是这样想的,别人是怎样想的?我的想法发生了怎样的变化?我是否有新的想法?学生理解他人的思考方式,反思自己的思考过程,认识并体验数学思考的基本方法。
(作者单位:南京师范大学附属小学)
责任编辑:赵继莹
724132105@qq.com

