基于空间转换模型的工业机械臂手眼标定方法研究

王任远 肖正航 吴杰 李沛

（北京空间机电研究所，北京 100094）

0 引言

近年来，超大口径的空间遥感技术研究由大口径单体反射镜向空间分块式反射镜发展[1]，以詹姆斯·韦伯太空望远镜（JWST）为代表的空间分块可展开成像技术已开展工程研制，同属分块式反射镜技术的在轨装配技术复杂度更高，仍处于论证阶段，需要在地面进行大量的实验论证其可行性。

工业机械臂技术近年来取得长足发展，已经广泛应用于制造业各个领域的装配工艺环节，能够实现大质量、大尺寸的零部件的装配[2]。工业机械臂绝对定位精度低、重复定位精度高，利用其重复定位精度高的特点，批量的装配应用大多利用示教的方式[3-4]。而在单件装配应用场景下，如大尺寸飞机零件装配[5-7]、大口径分块式反射镜的装配等场合，需要绝对定位精度高，一般的工业机械臂就不能满足要求，就需要采用单目、双目或多目相机组成摄影测量系统进行实时位置引导[8-11]。装配系统精度的提升是实时引导装配中需要解决的一个关键问题，国内外众多学者对系统中单个误差项的研究较多，但对于系统中各误差的关系与综合精度方面的研究较少。

如在机械臂绝对定位精度方面，通过建立工业机械臂的运动学模型，建立笛卡尔空间与关节空间的映射矩阵，是进行误差修正的前提；利用运动学模型推导误差模型并设计相应的补偿算法和数学逼近法已经是相当成熟的方法[12-13]；引入优化算法如LM算法优化参数识别效果能显著提高机械臂的绝对定位精度[14]；随着智能算法的研究深入，神经网络算法与空间插值算法那也渐渐成为研究主流[15-17]。

在机械臂引导系统的研究上，大多基于摄影测量系统进行设计。最基本的方法是基于图像的点特征进行识别并引导测量机械臂位置与姿态[18-19]；将摄影测量系统结合结构光系统（如激光投影或条纹格栅式光源投影）可以有效提高引导系统的测量精度[20-22]。除了基于摄影测量系统，利用激光跟踪仪等高精度测量设备对工业机械臂末端姿态进行测量[23-24]，并搭建的闭环控制系统进行位姿误差补偿也成为近期研究的热点。而在综合精度研究方面，文献[25]也仅验证了机械臂运动学标定与手眼标定精度的相关性。

本文针对一种面向大口径分块式反射镜的基于摄影测量系统引导的双机械臂自动装配系统进行系统建模与标定。通过将机械臂运动学模型、相机成像模型与eye-to-hand形式的手眼模型作为整体进行建模，分步对它们进行参数标定，为分块式反射镜在轨装配技术工作进行基础技术研究与地面原理验证。

1 系统组成与系统空间模型建立

1.1 系统组成

装配系统一般包括运动执行子系统、引导测量子系统、计算机控制端和辅助装配子系统几部分组成，如图1所示。本文研究的分块式反射镜主体长2.5m，高3.75m，待装配的单块分块镜联合工装质量约88kg。

运动执行子系统采用两台质量150kg、最大工作范围为3m的机械臂协同完成装配。基于双目视觉相机搭建了用于实现工件、机械臂末端的空间定位功能和对机械臂末端移动位置实时测量和引导的引导测量子系统。

以图1中右侧工件装配为例，进行装配时，机械臂A夹持待装配工件，机械臂B夹持双目视觉相机，通过双目视觉相机对工件位置的测量，将测量信息发送位置指令至机械臂A，引导机械臂A完成装配工作。

图1 在轨组装地面原理验证系统布局示意图Fig.1 Layout of on-orbit assembly ground proof-of-principle system

1.2 系统空间模型的建立

系统空间模型包含三部分：相机成像模型、机械臂运动学模型和手眼关系模型。

1）相机成像模型如图2所示，由世界坐标系Ow-XwYwZw、相机坐标系Oc-XcYcZc、焦平面坐标系Omm-xy和图像坐标系Opixel-uv构成。

相机把物理空间中的三维点投影到成像平面之上，该模型可用式（1）表示，空间中一点P在世界坐标系下的坐标与其在图像坐标系即ZC=–f焦平面上的投影点的坐标间的映射关系为：

式中 (u,v)为点P在图像坐标系下的坐标；M1矩阵包含4个参数分别表示x轴上的归一化焦距、y轴上的归一化焦距、光轴光心在图像坐标系u轴上的位置、光轴光心在图像坐标系v轴上的位置，它们由相机结构决定，称为内参矩阵；M2矩阵包含2个参数R和t，它们分别表示相机坐标系与世界坐标系的旋转矩阵与平移向量，称为外参矩阵。

2）机械臂运动学模型采用Denavit-Havtenberg方法建立，简称D-H法。D-H法定义了机械臂的每个连杆坐标系由4个连杆参数描述，连杆长度ai和连杆扭转角αi用于描述连杆本身，连杆偏距di和关节角θi描述相邻连杆之间的关系，i代表第i个连杆。ai为沿Xi轴，从Zi移动到Zi+1的距离；αi为绕Xi轴，从Zi旋转到Zi+1的角度；di为沿Zi轴，从Xi-1移动到Xi的距离；θi为绕Zi轴，从Xi-1旋转到Xi的角度。其矩阵表示形式如式（2）所示，其中矩阵D为平移矩阵，矩阵R为旋转矩阵，其中矩阵用于表示在空间中的点从m坐标系向n坐标系的空间齐次坐标变换，即将点从m坐标系中的坐标转变成在n坐标系中表示的坐标变换矩阵。从连杆i向连杆i-1的坐标变换矩阵为

通过4个连杆参数将所有的连杆表示出来即可表示机械臂机构的位置关系与运动方式。本文采用的6自由度工业机械臂由6个连杆组成，且相互之间均为转动副连接。该机械臂的D-H模型参数如表1所示，机械臂运动学模型如图3所示，其中连杆4与连杆5的原点重合。机械臂从机械臂末端中心点（下文简称TCP点），到机械臂基座B的空间转换矩阵为

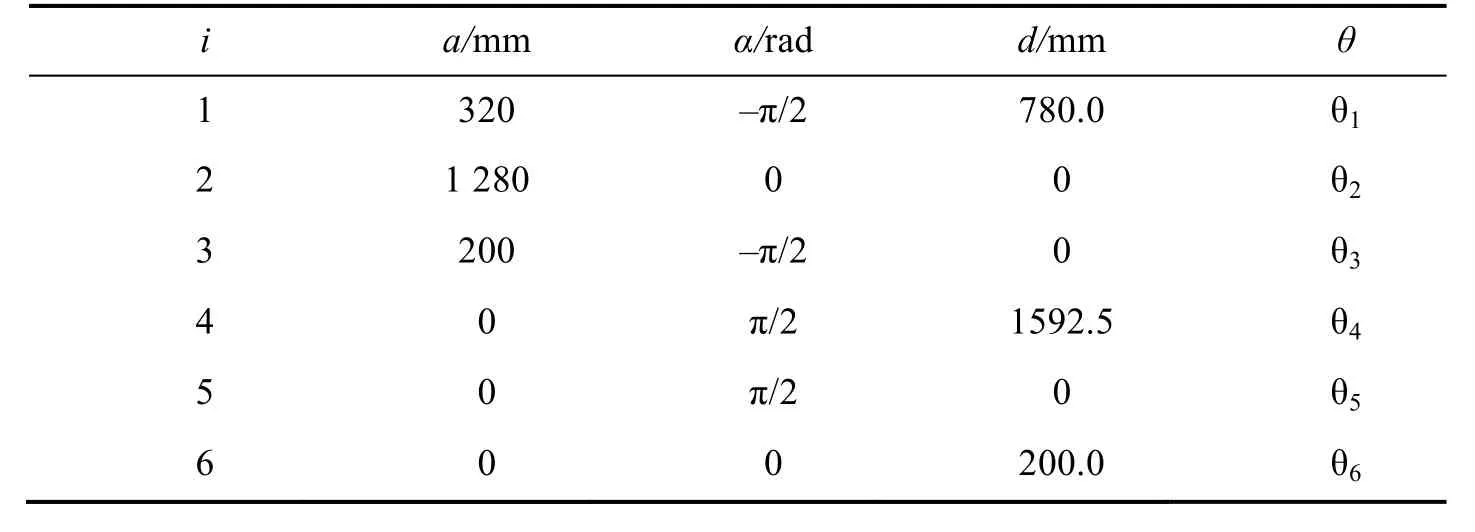
表1 工业机械臂D-H参数表Tab.1 Parameter table of Industrial manipulator by D-H method

3）Eye-to-hand形式的手眼位置关系如图4所示，由机械臂基坐标系OB、机械臂末端TCP点坐标系OT、标定坐标系OL和相机坐标系OC组成，可以得到手眼变换矩阵关系如式（4）所示：

图3 工业机械臂运动学模型Fig.3 Kinematics model of industrial manipulator

4）基于手眼标定关系的模型统一：手眼标定过程中求解标定靶球位姿的过程，实际上是一个计算相机坐标系OC与世界坐标系OW之间转换关系的过程（将靶球坐标系与世界坐标系重合），因此在机械臂手眼关系中，标定靶球的位姿矩阵就是相机模型的外参数M2矩阵，因此将式（4）代入式（1），可得

同时，将式（3）带入式（5），得到整体建模的最终变换关系，

图4 Eye-to-hand手眼坐标关系图Fig.4 The eye-to-hand coordinate diagram form

根据式（6）可知，标定靶球坐标系通过各转换矩阵与像平面坐标系建立了映射关系。由此，建立了基于机械臂运动学模型、相机成像模型与eye-to-hand形式的手眼关系模型。

其中，手眼标定就是求解机械臂基坐标系OB向相机坐标系OC的空间齐次坐标变换CBT的过程。根据式（4），任取位置i和位置i+1的转换关系，联立方程，如式（7）所示：

未经运动学标定的重载工业机械臂的绝对定位精度一般大于1mm[27]，不能满足本项目需要。需要对机械臂进行运动学标定提高绝对定位精度，并通过高精度手眼标定进一步提高装配精度，引导机械臂完成装配工作。

2 系统标定与装配实验

2.1 机械臂运动学标定

利用递推最小二乘法对机械臂末端进行运动学标定，式（4）的函数形式如式（8）所示：

而机械臂在实际制造过程中因加工、装配等各个环节使得各参数产生了一定的误差，各误差积累影响了末端TCP点的实际位置。设各物理参量与理论值的微小偏差为dα、da、dθ、dd。因此TCP的实际位置为：

根据机器人微分运动学，可得到TCP与基坐标理论位姿与实际位姿的绝对定位精度误差ΔP关系：

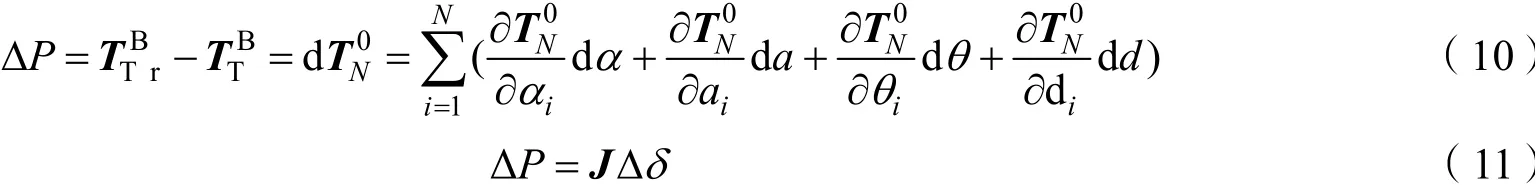
其中J为误差参数矩阵，δΔ 为包含所有的误差项。

通过构建超定方程组通过可递推最小二乘法对误差参数进行辨识与方程组求最小二乘解，形式如式（12）所示。

实验采用Leica AT401激光跟踪仪对机械臂TCP的实际位置进行测量，本次实验在机械臂工作空间设置40个样本点用于识别误差参数，采样点尽可能覆盖机械臂工作范围，分布如图5所示。

每达到一个样本点时使用激光跟踪仪测量靶标的实际位置，根据式（12）计算出各关节参数的误差值，最终通过将误差值预补偿至机械臂运动学模型的方式提高机械臂末端的绝对定位精度。辨识得到误差参数矩阵J如表2所示。重复实验，测得补偿后的机械臂末端TCP位置。补偿前后40个点与示教器显示点的误差如图6所示。

图5 40个采样点在空间中的分布图Fig.5 The distribution map of 40 sampling points in space

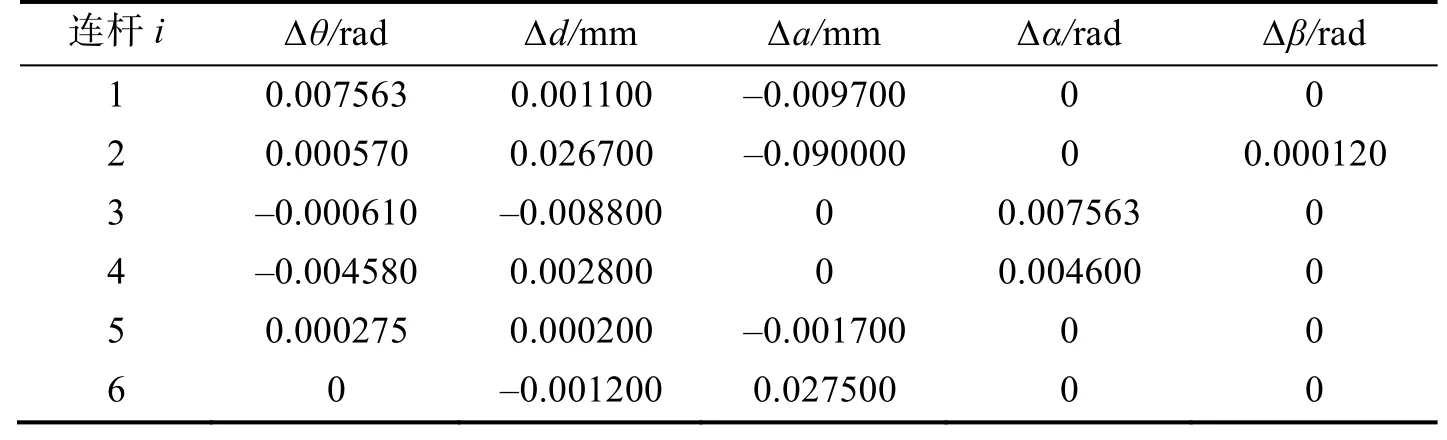
表2 误差参数辨识矩阵Tab.2 The error parameter identification matrix

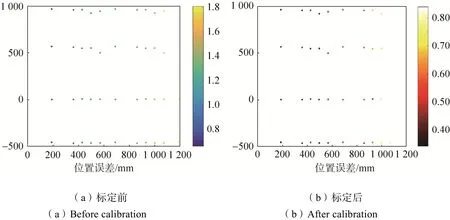
图6 标定前后位置误差对比Fig.6 Comparison of position errors before and after calibration

根据GB/T 12642–2001“工业机器人性能规范及其试验方法”中关于位置准确度（即机器人的绝对定位精度）的评定方法，点在空间中的理论位置(x,y,z)与实际位置(xr,yr,zr)的距离即定位误差

对测量结果进行分析可知，最大定位误差由补偿前的1.81mm降低至0.84mm，最小定位误差补偿后降至0.35mm。平均绝对定位精度由补偿前的1.19mm提高至0.55mm，提高了53.78%，机械臂绝对定位精度的提高有助于手眼标定精度的提高。

剔除少部分坏点后，对数据分析可知，当机械臂末端远离机械臂基座时，其绝对定位精度逐渐下降。这主要是因为末端重载的串联机器人为悬臂梁结构，随着末端与基座的远离，臂长增加，弯矩增加，末端绝对定位精度降低。由此可知，将机械臂对称布置，每个机械臂负责临近区域的装配是一种绝对定位精度更高，更合理的布局形式。

2.2 手眼标定与实验

在完成机械臂运动学标定的基础上，进行手眼标定。手眼标定的过程如图7（a）所示，在保持基坐标系与相机坐标系位置不变的情况下，控制机械臂末端带动标定靶标运动，在n个位置测量靶标和读取相应的机械臂关节参数。

手眼标定过程中，机械臂夹持靶球应进行至少两组旋转轴不平行的运动[6]，通过求解机械臂空间基坐标系OB与相机坐标系OC的变换关系。本文采用经典的Tsai两步法，结合机械臂运动学标定后的运动学模型与相机模型，完成手眼标定，如图7（b）所示。

为验证手眼标定有效性，设计轴孔对插实验验证标定后的系统工作精度。

图7 手眼标定过程和靶标球Fig.7 Hand eye calibration process and the target ball

轴孔对插实验如图8所示，在机械臂末端执行器安装实测尺寸直径为7.92mm的定位轴，在工作平台放置一块预先钻孔的工装板，孔的大小按照直径8.1mm~9mm依次排列。采用Leica AT402激光跟踪仪测量孔的位置和完成轴孔装配后轴的位置，选取2个装配位置进行测量。

图8 摄影测量系统引导的孔轴对插实验Fig.8 The experiment of hole axis pair insertion guided by the photogrammetry system

实验结果如表3所示，可以成功完成实测直径为8.34 mm和8.38 mm的孔轴装配工作。

表3 孔轴位置测量坐标值Tab.3 Coordinate values of hole axis position measurement

完成高精度手眼标定后，机械臂系统在摄影测量系统引导下，在XOY平面装配精度由章节2.1中测量的最大定位误差1.81mm大幅降低至0.29mm，提高了83.98%。标定前机械臂工作的定位误差大于1mm，无法满足任务需求，在完成手眼标定后，可以将装配系统用于大尺寸分块式反射镜装配的地面原理验证任务。

4 结束语

本文通过相机模型、机械臂运动学模型和手眼关系模型建立了基于装配系统的空间转换模型，通过递推最小二乘参数辨识方法将机械臂的平均绝对定位精度由补偿前的1.19mm提高至0.55mm，提高了53.78%；在此基础上，利用空间转换模型完成了高精度手眼标定，并设计轴孔对插实验验证标定后的装配系统精度，平均定位误差由1.81mm降低至0.29mm。可应用于大尺寸分块式反射镜系统的视觉引导装配，为空间在轨装配工作进行技术研究与地面原理验证。