基于空间反射镜的点阵结构非均匀尺寸优化设计

张牧尧 苏云 王超

（北京空间机电研究所，北京 100094）

0 引言

空间反射镜作为光学遥感系统的主要零部件之一，对于成像品质有着重要意义。反射镜的质量作为重要指标，决定着航天器的发射成本与光学相机的成像品质。因此反射镜结构的轻量化设计是如今光机结构设计的关键步骤。

轻量化设计作为航空航天业内的传统课题，一般通过选择轻质材料以及结构优化设计两种方法实现。从材料的角度，采用如钛合金、陶瓷、碳纤维复合材料等轻质材料可达到轻量化的目的。而从结构设计的角度，点阵结构作为新兴结构形式，可以在实现减质量的同时保持结构的承载力，实现轻量化和结构性能的完美平衡。该结构由节点和杆件作为基本元素构成，一般通过使用不同的单胞构型实现结构的功能性变化，特点是质量较小、比强度高以及特定部位的刚度高，并且能带来许多热力学特征。增材制造（3D打印）的快速发展给点阵结构的制备提供了实现的条件，使设计人员能够尝试一些颠覆性的点阵设计方案。国内外学者使用点阵结构设计了许多航空航天零部件[1]，如：文献[2]在航空涡轮发动机上使用了点阵技术；文献[3]使用点阵结构轻量化处理制造了小型反射镜，并对其进行了光学表面的镀镍处理以及X射线探伤；文献[4]在设计相变热控制器时填充了点阵结构，实现了60%的轻量化率，并且结构在受压实验中表现良好，防漏性能令人满意。传统点阵材料为均匀分布，但是非均匀点阵结构有着更好的力学性能，可以根据结构特性达到更好的材料分布[5-7]，一般用拓扑优化实现点阵结构的非均匀性。在结构拓扑优化方法中，主流手段为变密度法中采用的固体各向同性材料惩罚模型（Solid Isotropic Material with Penalization，SIMP）[8]、水平集法[9]等：文献[10]提出一种新的变密度点阵结构的拓扑优化方法，通过3D打印制造出具有变密度点阵的汽车连杆；文献[11]使用多尺度点阵拓扑优化方法优化了点阵结构，得到胞元结构在点阵之中的最优分布。移动阈值切面法（Moving Iso-surface Threshold Topology, MIST）[12]是一种新型的拓扑优化方法，它无需在显示灵敏度分析的条件下完成结构的拓扑，而且算法难度不大，利于工程人员在商业有限元软件上实现。

综上所述，点阵结构已经在航空航天领域得到了很多应用，主要体现在新设计提升了结构的刚度以及轻量化率。但是，在结构的功能性上，如提升结构的力热稳定性方面还未有更多的突破。本研究致力于在使用点阵结构实现轻量化设计之外，通过一定程度的优化安装应力，实现结构功能以及轻量化一体化设计。

由于传统的背部开口轻量化形式不足以达到指标要求，故对于空间反射镜进行了均匀点阵填充设计，之后基于MIST法对反射镜进行了非均匀点阵结构尺寸优化，在保证面形精度的条件之下，有效地提升了轻量化率，提升了结构刚度，最后在有安装应力的工况下验证了结构性能。

1 反射镜优化算法的数学模型

使用点阵结构设计反射镜结构与传统反射镜轻量化孔的设计方法不同，需要将传统反射镜参数分解到每一根点阵单胞的杆件之上，所以需要针对点阵结构组成的反射镜建立优化的数学模型，并对于结构的安装应力进行分析计算。

1.1 MIST法模型

2013年，仝立勇教授提出了MIST法[12]，作为拓扑优化方法中的一种，它旨在找到元素的权重因子x与等值面S的阈值t，使得结构设计中的某个变量J（如结构应变能）最小化，约束条件则为结构的材料约束gs以及有限元方程gr。具体形式为：

式中xl为结构参量的最小值；xu为结构设计参量的最大值。

MIST法定义了一个响应函数的曲面φ（一般为应力或者应变能的函数），然后使用一个等值面S去切割该响应函数，它们相交的轮廓作为结构的边界。MIST法迭代开始前的初始化中，对于设计空间进行有限元网格的划分并存储节点单元信息；与SIMP法的相似之处是，MIST法在每一个有限元网格之中均设置了权重因子x，该值若为0，则相当于拓扑优化中的孔洞材料（该单元无结构材料分布），若为1，则相当于拓扑优化中的实体材料分布（该单元有结构材料分布）。之后在每个有限单元节点上计算响应函数的值，并生成响应函数的曲面φ；然后使用等值面S切割响应函数曲面φ，等值面S的阈值t由结构的体积约束决定，在权重因子x更新的过程之中，所有元素单元的响应函数值大于等值面的阈值t时让单元向实体材料方向演变（权重因子变向1），当单元的响应值小于等值面的阈值时让单元向孔洞材料方向演变（权重因子变向0）。若单元中的响应值既有在等值面阈值之上以及等值面阈值之下的，权重因子x则为在等值面阈值以上部分的响应函数的投影面积分数。若x和t的值均收敛则结束循环，否则进入下一循环。

MIST法的具体操作流程图如图1所示。

等值面S对应的阈值t使用二分法进行计算，具体计算方法如下：

1）令tmax0= max(φ),tmin0= min(φ)，其中tmax0和tmin0为二分法首次迭代的参数。2）计算水平等值面对应的阈值。其中tk为k次循环时的阈值。

3）在全部有限单元计算域内计算φ-tk的值，若计算值均为正，则该单元节点为实体则增加xjk；若计算值均为负为孔洞则减少xkj；若有正有负则根据两部分对应面积的比例计算。其中xkj为k次循环时第j个单元的权重因子值。

4）若迭代到k次循环时的结构总体积kV、结构总体积

约束Vcons与二分法的收敛指标数ζ满足则结束循环。

1.2 基于MIST的点阵杆件结构优化方法

本文基于MIST法对于反射镜的点阵结构进行了杆件的尺寸优化。点阵结构的主要参数为杆件长度以及杆径大小，故将杆件的横截面积作为MIST法之中的权重因子。优化模型之中包含了结构的体积约束，杆件截面积的下限一般由增材制造的工艺水平决定。

点阵优化算法的数学模型列式如下：

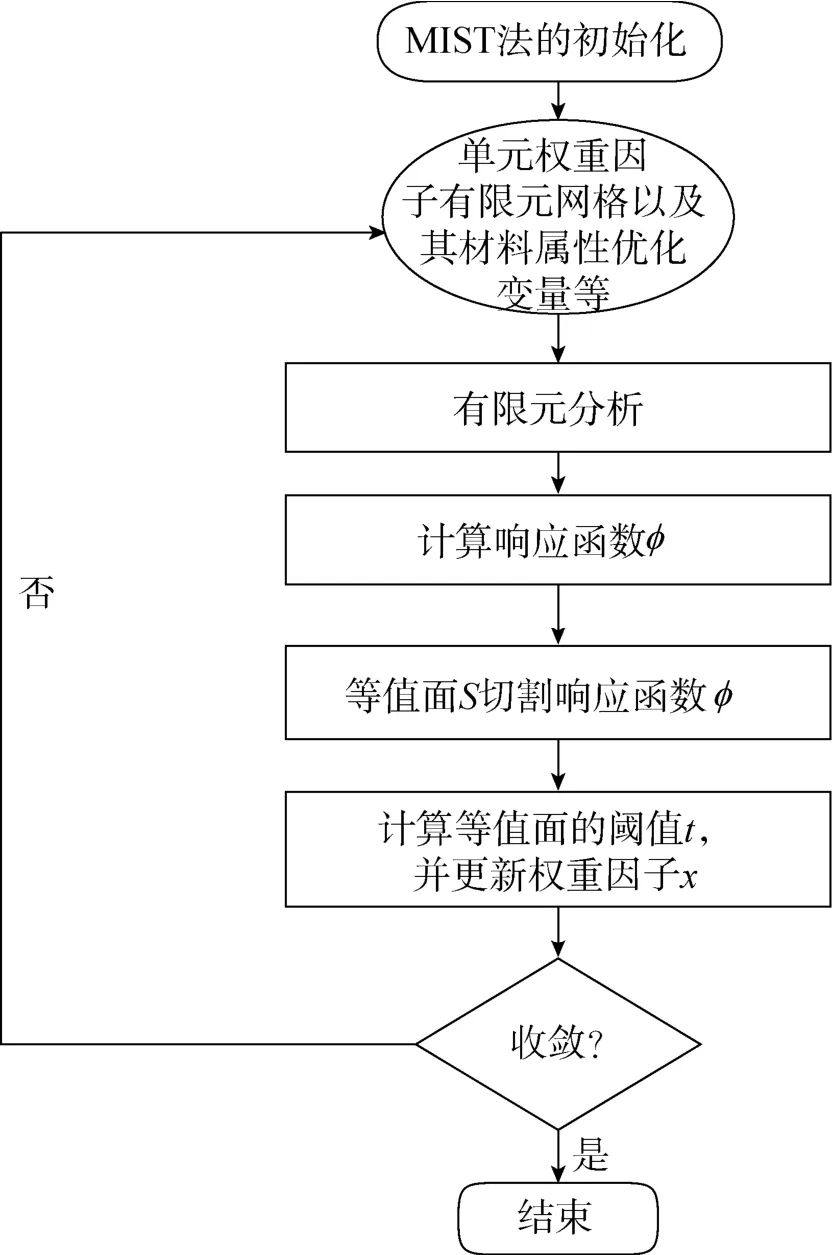
图1 MIST法优化流程Fig.1 Flow chart of MIST method optimization

式中 设计变量iA为杆件的横截面积；f(r)为结构总形变势能；F为结构的外载荷向量；K为有限元结构的总体刚度矩阵；U为有限元节点位移向量；Li为点阵单胞杆件的长度；为点阵杆件的体积约束；aA为杆件横截面积上限；bA为杆件横截面积下限。本文使用结构的形变势能作为结构优化模型的响应函数，故根据材料力学，它的具体表达式为：

式中iF为杆件受到的轴力；E为材料的弹性模量。点阵优化模型的目标函数为结构的固有频率（刚度）最大，根据式可知刚度最大可转化为形变势能最小。

1.3 拧紧力矩M

对于空间反射镜的安装来说，镜面面形精度一般要求为纳米级别，所以不仅要保证连接部件的螺钉强度足够抵消发射振动，还要准确控制预紧力矩，以免对于反射镜面形造成精度缺失。金属反射镜与镜框之间的连接方式为螺栓连接，将反射镜使用螺栓连接至镜框上时，需要克服螺纹的螺纹阻力矩M1以及螺钉头和连接件支撑面的摩擦力矩M2。其中，拧紧力矩M可以用如下形式表征[13]：

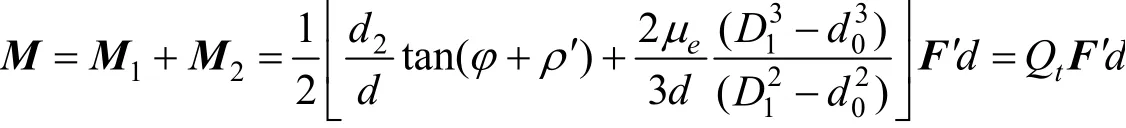
式中F'为螺钉的预紧力；d2为螺纹中径；d为螺纹大径；φ为螺纹升角，其中P为螺距；ρ'为螺纹副的当量摩擦角，ρ' = arctanμ，其中μ为螺纹当量摩擦因数；μe为螺钉头与联接件支撑面之间的摩擦因数；1D为螺钉头联接面的外径；d0为钉孔直径；tQ为拧紧力矩因数，与螺钉尺寸、螺纹副和支撑面的摩擦因数等有关。

2 反射镜结构的优化分析

2.1 优化方案

本文中的反射镜在自由边界条件之下，主镜频率要高于550Hz，质量不能超过850g，面形均方根误差故使用基于MIST的优化方法对于190mm铝合金反射镜进行结构优化设计。反射镜材料采用可增材制造的AlSi10Mg，材料参数弹性模量为62GPa，泊松比为0.32，目标后续以3D打印制备反射镜。反射镜采用侧面三点支撑方法。根据设计经验，反射镜设计模型之中初始侧面壁厚为2mm，镜面厚度为4mm，设计空间边缘厚度为3mm，反射镜的初始结构如图2所示。

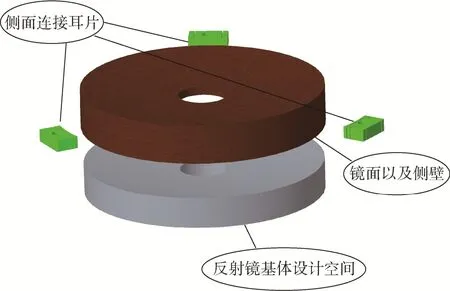
图2 反射镜初始结构示意Fig.2 The initial structure of space mirror schematic

使用3-matic软件对设计空间进行均匀点阵结构的填充，设计空间为实体镜坯。图3单胞为6mm×6mm×6mm的BCC点阵单胞，填充整体设计空间后，单胞个数为220个，边缘处点阵分布5层，中心处点阵分布4层。点阵边界处使用基于表面网格的方式处理，手动将边界网格节点连接至单胞节点之上，最后填充之后的整体点阵如图4所示。可以看到，除了在反射镜与实体接触部分使用了表面网格的形式填充，其余点阵单胞均匀分布在反射镜内部结构之中，此填充模型将作为下节点阵横截面积优化的初始输入。

图3 BCC单胞示意Fig.3 BCC lattice cell structure

使用基于MIST法对于点阵结构进行非均匀尺寸优化，优化问题描述如下：外载荷为螺纹孔处的安装应力，基于卫星环境规范以及拧紧力矩的计算公式计算得扭矩2.5N·m，约束条件为镜面位移最小以及点阵结构体积（质量）上限值，目标函数为点阵结构的总应变能最低（刚度最大），设计变量为点阵结构的杆件截面积局部最优。初始设置杆件的直径为1.2mm，根据工艺要求，杆件直径最小为0.8mm，最大为2.4mm。使用优化程序优化杆径变量，经过300次迭代过后，得到的点阵优化结果如图5所示。

图5 中点阵结构杆径的大小分布非均匀性明显，在螺栓耳片位置以及中心孔附近的杆径明显大于其他位置的杆径，结果与预期设计相符合。结合连续体的拓扑优化结果，外观也是相似的。表1为优化前后均匀点阵与非均匀点阵的设计结果对比。

图4 均匀点阵填充反射镜结构Fig.4 Uniform lattice infill space mirror

图5 优化后的非均匀点阵Fig.5 Non-uniform lattice after optimization

表1 点阵优化设计参数结果Tab.1 Parameters result of lattice optimization design

表1 中，优化之后的非均匀点阵结构中单胞个数仍为220个，杆件个数为1129，杆件截面直径最大为1.8mm，最小为0.8mm。优化后的刚度相对于均匀点阵结构提升明显。

2.2 性能分析以及对比

为了模拟反射镜安装状态，对于优化结果进行安装应力的工况分析。不同于以上优化工况，选择在螺纹孔处施加0.01mm的法向强迫位移模拟安装，另外附加沿Y轴向下的重力（反射镜光轴竖直状态）。在此工况下，对比分析传统背部轻量化形式以及非均匀点阵结构形式的反射镜的面形精度。有限元分析得到的节点位移仅为节点各个自由度的位移量，包含了结构的刚体位移，故对于节点位移进行处理，使用基于Zernike多项式拟合的仿真技术得到反射镜面形，见表2。

表2 两种结构面形精度以及质量对比Tab.2 Comparison of mass and surface shape between two sturctures

表2 对两种质构形式的质量以及刚度进行了对比，统背部开口形式反射镜和点阵结构反射镜均可以满足结构刚度和面形的要求，而经过非均匀点阵结构尺寸优化的反射镜镜面面形比起常规形式来说，质量减少了20%，轻量化率得到了明显提升。由此可见，非均匀点阵反射镜结构应用于小口径金属反射镜上，具有着轻量化以及功能化的优势。图6为两种结构形式的反射镜节点位移对比。

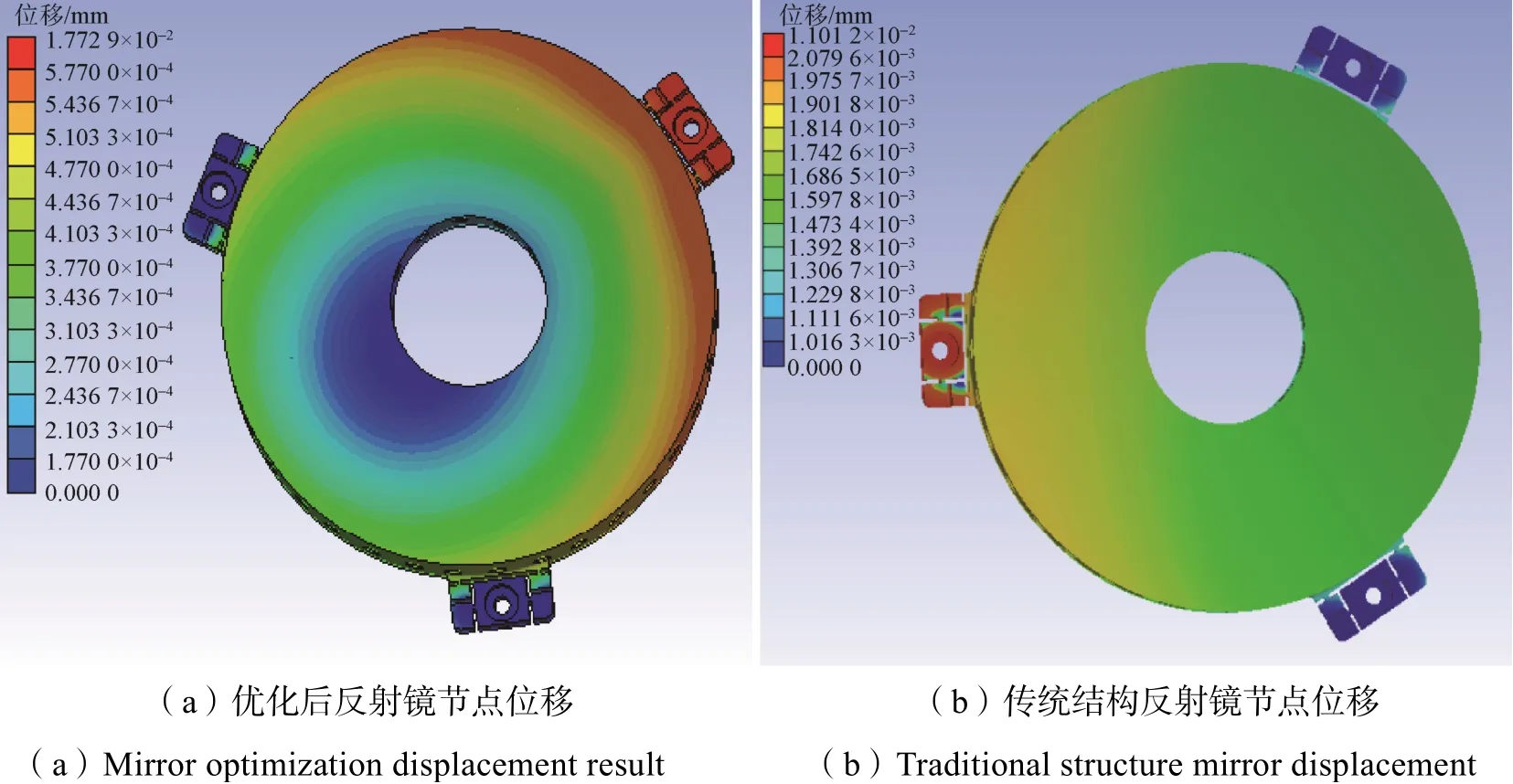
图6 优化后反射镜节点位移Fig.6 Mirror optimization displacement result

由图6（a）优化后的非均匀点阵结构节点位移云图与图6（b）所示的传统点阵结构节点位移云图的对比来看，除了施加强迫位移处的最大节点位移相似，其余节点均有着不同程度的减少，在中心孔处的节点位移优化程度尤为明显。

为了分析非均匀点阵结构对于不同安装应力的面形精度影响，改变了强迫位移的大小，如图7所示，当施加少于0.01mm的强迫位移时，非均匀点阵结构和传统结构的面形精度较为一致，但是随着强迫位移的逐渐加大，非均匀点阵结构的面形精度的优势越为明显，可以承受更高的安装应力。

由图6~7以及表2可以看出，使用了非均匀点阵结构尺寸优化的金属反射镜，镜体节点变形量显著下降，刚度得到了明显提升，验证了优化目标函数的合理性。

图7 两种结构在不同强迫位移下的面形对比Fig.7 Comparison of surface shape of two structures under different forced displacements

3 结束语

本文基于MIST法对于空间金属反射镜进行了非均匀点阵结构尺寸优化设计，在轻量化的同时提升了反射镜的刚度，获得了较好的面形精度，且有效抵消卸载了部分安装应力。与传统的蜂窝式轻量化结构形式相比，具有设计裕度大、针对目的性强等优势。点阵结构的形式可以推广到整个相机结构以及其他部件之上，使得整体光机结构获得更高的结构性能。