硬式飞艇氦气囊的非饱和形态研究

唐旭 张红英 陈建平 童明波 宋海洋

（1 南京航空航天大学航空学院，南京210016）

（2 中国人民解放军JHJ装备部驻武汉地区J事代表局驻武汉地区第五J事代表室，武汉430000）

0 引言

硬式飞艇一般由刚性骨架和外罩蒙皮构成，艇体骨架内安装一系列密闭的氦气囊[1-3]。氦气囊内部充氦气用于产生净升力，其安全性事关整艇安全。飞艇升空前，飞艇内部的氦气囊充气比例（饱和度）小于100%，氦气囊是非饱和的[4-6]，这就给飞艇氦气囊的结构、氦气囊间的约束方式以及浮心和重心的确定带来了极大困难。因此，深入研究飞艇氦气囊的非饱和形态，对硬式飞艇设计显得尤为重要。

近年来，学者们展开了许多对浮空器囊体的非饱和形态研究。文献[7]采用修正褶皱单元的本构矩阵方程的方法，对非饱和氦气球的褶皱区域进行处理，与地面充氦试验对比效果较好；文献[8]采用压差梯度法，研究了不同零压面位置的柔性飞艇形状的变化规律，分析结果与试验结果吻合较好；文献[9]基于最小势能法，对自然形高空气球的非饱和形态进行了研究。

上述研究均是对模型进行了一定程度的简化，且未充分考虑囊内外气体对气囊的耦合作用，实际上对于飞艇气囊这一大曲率、大体积柔性充气结构，其流固耦合效应十分显著。囊体充气、泄气过程是典型的流固耦合过程，任意拉格朗日–欧拉（ALE）法可以有效处理囊体类柔性结构与流体间的非线性耦合问题[10-13]。文献[14]采用ALE方法模拟了安全气囊展开和冲击过程；文献[15]采用ALE方法模拟了普通气囊充气的过程；文献[16]在气囊底部建立了气体发生器，采用ALE方法对驾驶员侧气囊展开进行了数值模拟。本文研究的氦气囊其充气前形状不规律导致气体发生器的尺寸和位置不易确定、气囊饱和度低时气体易穿透、钢架绳索对囊内气体运动造成阻碍等原因，采用ALE法模拟氦气囊的充气过程较为繁琐，难度较大。

为了解决上述问题，本文利用控制体积法（Control Volume，CV）得到氦气囊的饱和形态，再建立氦气囊泄气流固耦合模型，充分考虑囊体与内外部流体间的非线性耦合作用，开展不同饱和度（90%、80%、70%）氦气囊的形态研究，同时对多氦气囊组合变形进行预测。

1 数值计算方法

1.1 流固耦合控制方程

ALE方法的流体控制方程由质量方程、动量方程和能量方程组成[17-19]

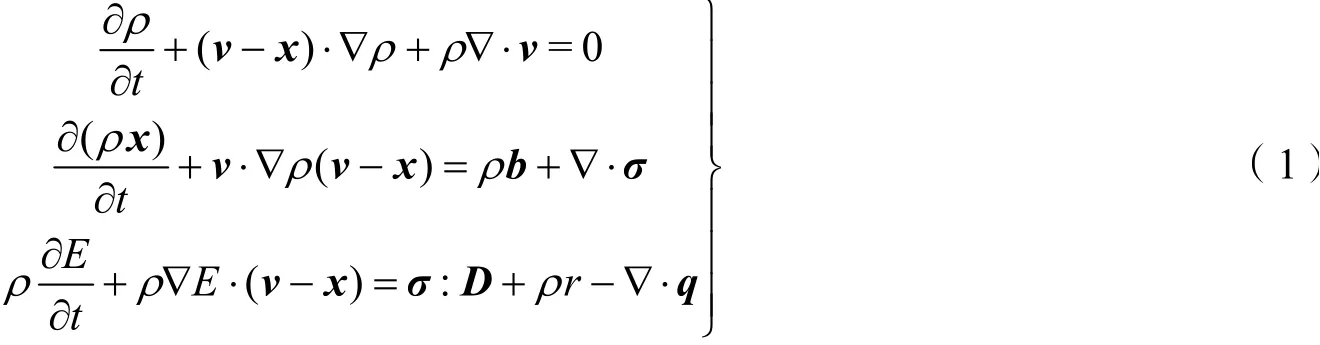
式中v为流体质点的物质速度；x为网格速度；ρ为物质密度；b为外部体积力；σ为柯西应力张量；E为材料内能；D为材料应变率；r为单位质量的热生成率；q为热流矢量；t为时间。

1.2 流固耦合方法

基于罚函数的耦合算法可以有效处理流体与固体的耦合过程，当流体物质点穿透结构单元时，在穿透节点上会产生一个反向作用力，反向作用力的大小正比于穿透量Y。根据流体边界与结构点的相对位移计算出的数值耦合力Fc[20-22]为

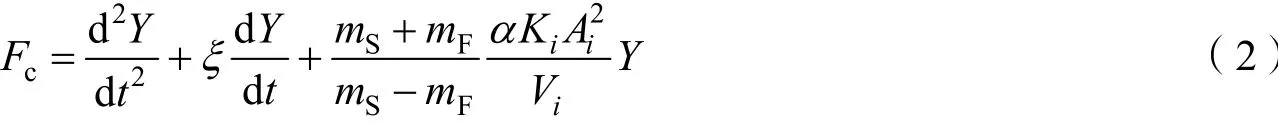
式中ξ为阻尼系数；mS和mF分别为固体和流体质量；α为缩放质量；Ai、Vi、Ki分别为单元面积、单元体积和单元容积模量，下标i代表不同的单元。耦合力既作用在流体单元上也作用在结构单元上，它们是一对作用力和反作用力。

1.3 压力梯度与气体流动模型

重力引起的压力梯度是产生浮力的根本原因，压力梯度会对飞艇气囊外形造成影响。压力梯度由气囊内外密度差决定（如图1所示），可由式（3）确定

式中 Δp为囊体内外压力差；Δp0为气囊横断面底部压强，由气体状态方程求得；ρair为气囊外大气密度；ρhe为气囊内氦气密度；g为重力加速度；zh为囊体的高度；zt为所求点的高度，下标t代表不同的高度。

氦气和空气可视为理想气体，理想气体状态方程为

式中pq为理想气体压强；CPq为气体比定压热容；CVq为气体比定容热容；ρq为气体密度；Tq为气体温度；q代表不同的气体。

2 数值计算模型与试验方法

2.1 飞艇气囊模型

硬式飞艇内置多氦气囊布置形式如图2所示，艇体内部有多组氦气囊，内置氦气囊的类型主要分为整体式和左右对称式。

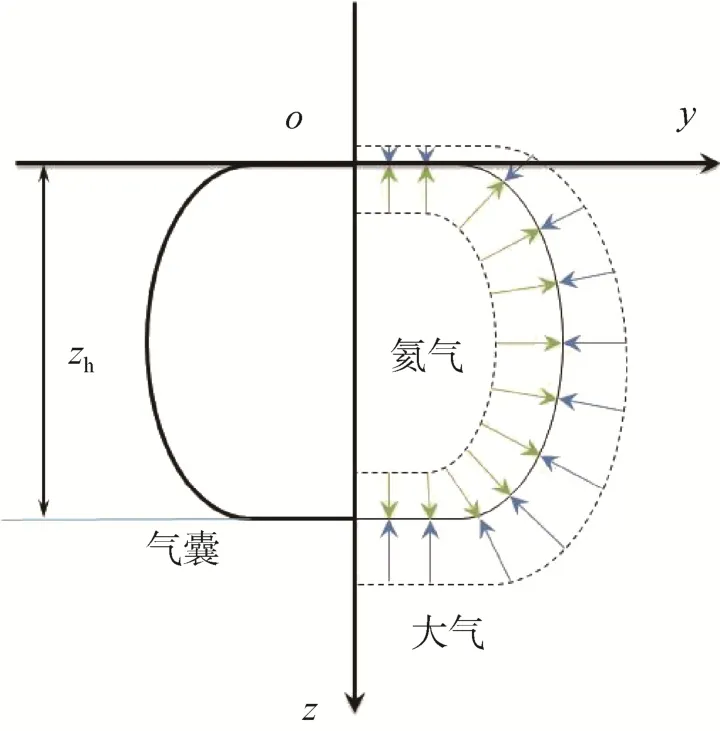
图1 囊体内外压差分布Fig.1 Differential pressure distribution inside and outside the helium bag

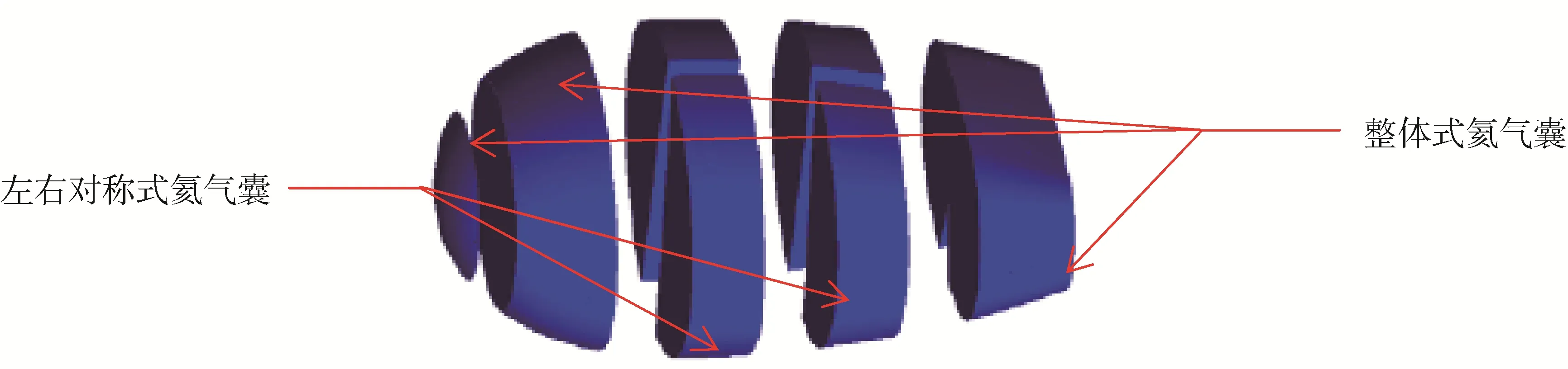
图2 内置氦气囊模型Fig.2 Built-in helium bag model

本文选取一对左右对称式异型氦气囊（如图3所示），囊体外部为钢架结构，钢架长6.32m，宽1.44m，高4.17m。为了约束氦气囊的运动，前后两端为绳索结构，氦气囊顶部与骨架通过蝴蝶绳进行连接，吊挂钢架中部。

图3 对称式异形氦气囊模型Fig.3 Symmetrical shaped helium bag model

2.2 折叠气囊有限元模型

采用直接折叠法建立气囊的有限元模型，在划分网格时按照折叠线进行网格划分，建模过程中，单元法向朝向封闭囊体外部。在软件LS-DYNA中利用织物材料关键字模拟气囊织物材料，单元类型采用膜单元；利用弹性材料关键字模拟绳网材料，单元类型采用绳梁单元，具体材料特性如表1所示。

表1 模型材料特性Tab.1 Model material properties

2.3 氦气囊泄气有限元模型

利用CV法得到气囊饱和形态模型后导出网格单元，消除个别单元间交叉和重叠现象，在气囊周围建立欧拉单元网格，流场计算边界采用无反射边界条件。

囊体在工作过程中与内外部流体之间是一个高度非线性的耦合过程，其中涉及的流体包括囊外空气及囊内氦气。包含流体的有限元模型如图4所示。通过软件LS-DYNA中的关键字初始体积分数法[23-24]来实现初始时刻囊内氦气的填充；为避免耦合计算过程中求解偏导数，利用LS-DYNA软件提供的空材料本构模型和状态方程来共同描述流体材料特性。对于囊外空气和内部氦气，状态方程采用理想气体模型进行描述。

试验过程中为了节约时间，采用电动气泵对气囊抽气，但是在仿真模型中建立抽气泵难度较大，所以对模型进行适当简化，根据文献[25]在气囊顶部建立排气孔，囊内氦气在内外压强的作用下排出囊外。

2.4 试验方法

地面充氦试验主要在自行研制的平台上完成，试验环境和试验设备如表2所示。由于试验在室内进行，且充气时间较快，所以温差对压差的影响不大，试验过程中忽略囊体的透氦性。试验共包括两部分：充气试验和泄气试验。

充气试验：氦气保障车在充气泵的作用下，以一定的质量流量向囊内充氦，照相机记录气囊的形态变化，位于囊体上部的测压管和测压计记录囊内气压的变化情况。充气试验开始前，电子秤显示钢架和气囊的总质量，随着充气的进行，在大气浮力的作用下，电子秤的数值会逐渐变小。根据阿基米德原理（气囊所受到总浮升力的大小等于囊体排开空气的质量）差值计算出气囊充氦的体积、质量。

泄气试验：以充气试验得到的飞艇氦气囊饱和形态作为初始形态，在抽气泵的作用下，氦气囊以一定的质量流量向外均匀泄气，根据电子秤的数值计算出气囊泄气的质量，从而得到气囊不同饱和度的体积。试验共得到3种不同的饱和度，分别是90%、80%、70%，当气囊达到指定的饱和度后停止泄气，记录囊体外形与囊内气压。

3 结果及分析

3.1 囊体充气过程

在充气试验开始前，囊内气体被抽气泵抽空，所以囊体并非完全压平折叠的状态，如图5（a）所示，氦气囊顶部部分固定在钢架上。由于氦气密度比空气轻，随着气体的充入，囊体上部最先展开，上表面褶皱较少，下表面褶皱较多，如图5（c）所示。在继续充入气体后，气囊上部最先饱满，气囊下部逐渐饱满，最终达到展平饱和的状态，如图5（g）所示，饱和状态的左右气囊相互挤压，它们完全展开的体积共28m3，两端绳索和钢架起到了约束气囊形态的作用。

仿真过程中采用 CV 法对折叠氦气囊进行充气，由于CV法采用的是理想气体均匀压力模型，所以充气过程中囊内压力均匀分布，气囊各部分均匀膨胀，在充气过程中，折叠部分的褶皱较多，如图5（d）、图5（f）所示，充气完成后最终达到饱和状态，褶皱部分变少，如图5（h）所示。

通过对比试验与仿真囊体充气过程可知，采用CV法对氦气囊充气不能够体现大气的浮力作用，也不能模拟囊内外气体同气囊之间的相互作用。但是利用CV法可以较快获得饱和气囊的外形，并且与试验得到的饱和外形相比，有较好的一致性，如图5（g）、图5（h）所示。所以可以采用CV法获得飞艇氦气囊的饱和形状，工程上有一定的借鉴意义。

图5 试验与仿真囊体充气过程Fig.5 Test and simulation of the inflation process of the helium bag

试验过程中测压计和测压管位于囊体顶部，选取囊体顶部代表囊内压力。试验与仿真过程囊内压力变化如图6所示。

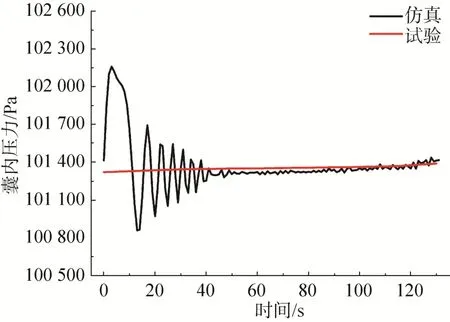
图6 试验与仿真过程囊内压力变化Fig.6 Test and simulation of the pressure change of the helium bag

由图6可知，仿真过程的前50s，由于囊体未完全展开，囊内压力产生振荡，当囊体逐渐展开后，随着气体的充入，其内部压力逐渐增大，在120s左右气囊基本达到最大体积。试验过程中囊内压力缓慢增大，最终达到101 393Pa。

3.2 囊体泄气过程

仿真和试验得到气囊的不同饱和形态如图7所示。

图7 试验和仿真气囊形状对比Fig. 7 Comparison of the test and simulation helium bag shapes

由图7可知，仿真过程中囊内氦气逐渐排出，囊体中下部在浮力及重力共同作用下“被顶起”，气囊饱和度为90%~70%时，仿真与试验得到的外形符合度较好。对比囊体泄气试验和数值仿真结果可以发现：泄气初始阶段囊体的外形变化较小，气囊中上部维持饱和形状不变，气囊底部及其两侧形状最先变化，囊体底部受到压应力导致囊体屈服而产生结构褶皱；随着氦气的持续抽出氦气囊整体饱和度逐渐降低，囊体底部被挤压的区域增大且底部褶皱也逐渐增多，同时囊体下部的收缩状态逐渐扩展到囊体中上部区域；泄气过程中气囊两端的绳网会对氦气囊形状有一定限制作用。

ALE方法中，选取与试验过程测压计相同位置的欧拉单元输出压力曲线，不同饱和度的试验和仿真囊内压力如图9所示。

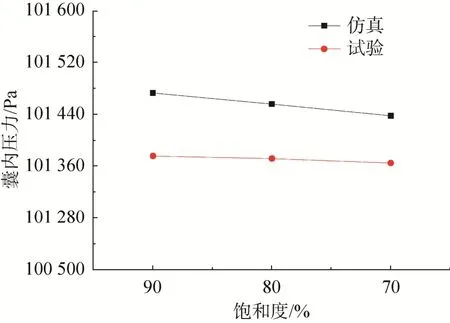
图9 不同饱和度囊内压力Fig. 9 Pressure in helium bag with different saturation

由图9可知，试验与仿真得到的囊内压力趋势一致，囊内压力都随着饱和度的下降而下降，两者误差在0.2%以内。

为进一步探究气囊泄气过程中的结构及流场的变化规律，选取气囊对称截面进行研究，截面的结构及流场变化如图10所示。

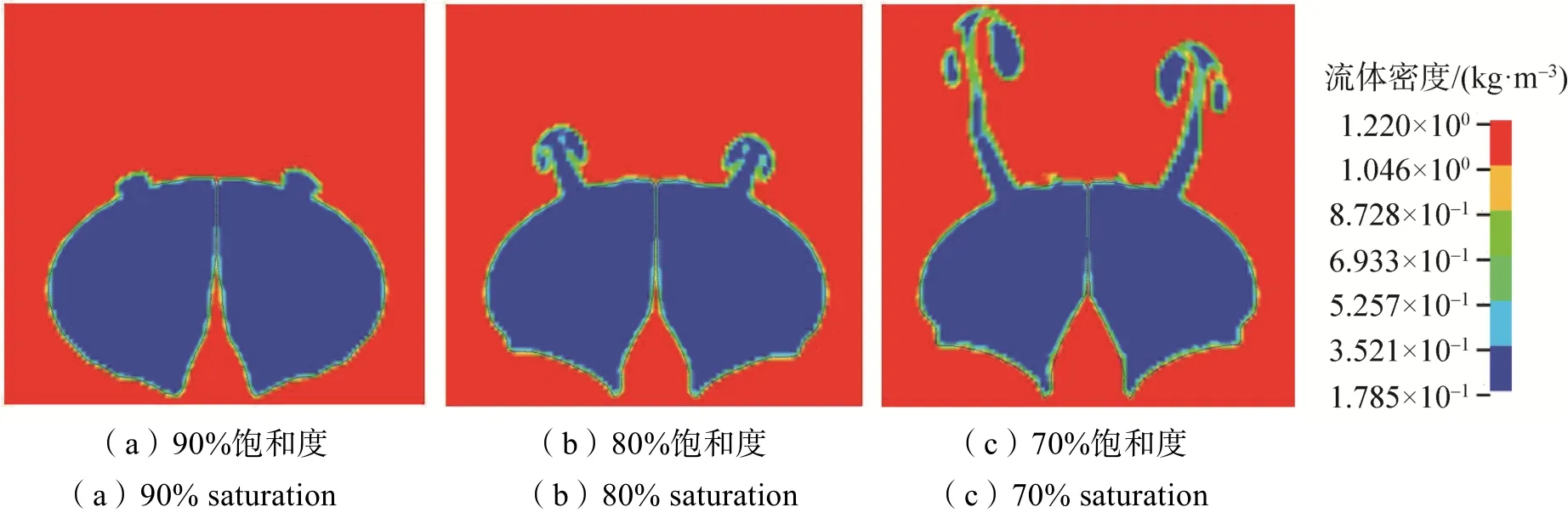
图10 对称截面的结构及流场变化Fig. 10 Structure and flow field changes of symmetrical section

从图10中可以看出，囊内氦气在内外压强的作用下，缓慢的冲出气囊顶部，之后会向上飘散，其流场分布及变化趋势符合工程实际。在泄气过程中外部流场稳定，囊内下部氦气向气囊上部流去。

4 结束语

本文通过仿真和试验方法研究了硬式飞艇氦气囊的非饱和外形，研究表明：

泄气初始阶段囊体的外形变化较小，气囊中上部维持饱和形状不变，气囊底部及其两侧形状最先变化，囊体底部受到压应力导致囊体屈服而产生结构褶皱。随着氦气的持续抽出氦气囊整体饱和度逐渐降低，囊体底部被挤压的区域增大且底部褶皱也逐渐增多，同时囊体下部的收缩状态逐渐扩展到囊体中上部区域。

气囊两端的绳网会对氦气囊形状有一定限制作用，但是氦气囊的中上部分仍会超出骨架两端，所以多个氦气囊进行组装时需要考虑囊与囊之间的相互挤压作用。目前国内外少有对硬式飞艇内置氦气囊进行形态分析，本文采用的ALE法可为飞艇氦气囊及氦气囊的布局形式提供参考。